文档内容
五年(2019-2023)年高考真题分项汇编
专题 02 函数概念与基本初等函数
函数概念与基本初等函数常考题型一般为选择题,中等难度,属于送分题。一般的出题类型为选择,填空。
对于函数周期与奇偶性以及综合应用一般难度比较大,技巧比较强。
考点 01 函数概念与单调性
1.(2023·全国·统考高考真题)设函数 在区间 上单调递减,则 的取值范围是( )
A. B.
C. D.
2.(2021·全国·统考高考真题)下列函数中最小值为4的是( )
A. B.
C. D.
3.(2021·全国·高考真题)下列函数中是增函数的为( )
A. B. C. D.
4.(2020·海南·高考真题)已知函数 在 上单调递增,则 的取值范围是( )
A. B. C. D.5.(2020·全国·统考高考真题)设函数 ,则 ( )
A.是奇函数,且在(0,+∞)单调递增 B.是奇函数,且在(0,+∞)单调递减
C.是偶函数,且在(0,+∞)单调递增 D.是偶函数,且在(0,+∞)单调递减
考点 02 函数周期性与奇偶性应用
1.(2023·全国·统考高考真题)若 为偶函数,则 ( ).
A. B.0 C. D.1
2.(2020·全国·统考高考真题)设函数 ,则f(x)( )
A.是偶函数,且在 单调递增 B.是奇函数,且在 单调递减
C.是偶函数,且在 单调递增 D.是奇函数,且在 单调递减
3.(2019·全国·高考真题)设 是定义域为 的偶函数,且在 单调递减,则
A.
B.
C.
D.
4.(2023·全国·统考高考真题)已知 是偶函数,则 ( )
A. B. C.1 D.2
5.(2022·全国·统考高考真题)已知函数 的定义域均为R,且
.若 的图像关于直线 对称, ,则
( )
A. B. C. D.6.(2022·全国·统考高考真题)已知函数 的定义域为R,且 ,
则 ( )
A. B. C.0 D.1
7.(2021·全国·统考高考真题)设函数 ,则下列函数中为奇函数的是( )
A. B. C. D.
8.(2021·全国·高考真题)设 是定义域为R的奇函数,且 .若 ,则
( )
A. B. C. D.
9.(2020·山东·统考高考真题)若定义在 的奇函数f(x)在 单调递减,且f(2)=0,则满足
的x的取值范围是( )
A. B.
C. D.
二、填空题
10.(2023·全国·统考高考真题)若 为偶函数,则 ________.
11.(2021·全国·统考高考真题)已知函数 是偶函数,则 ______.
考点 03 函数图像应用
一、单选题
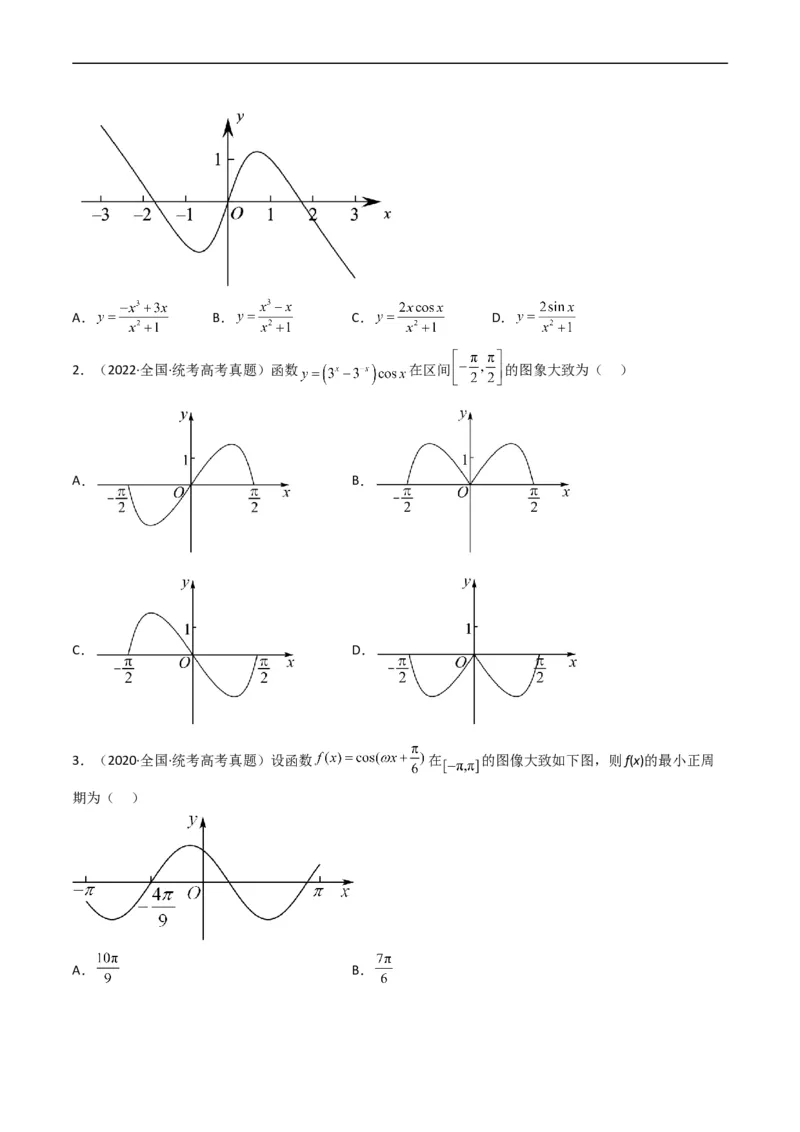
1.(2022·全国·统考高考真题)如图是下列四个函数中的某个函数在区间 的大致图像,则该函数是
( )A. B. C. D.
2.(2022·全国·统考高考真题)函数 在区间 的图象大致为( )
A. B.
C. D.
3.(2020·全国·统考高考真题)设函数 在 的图像大致如下图,则f(x)的最小正周
期为( )
A. B.C. D.
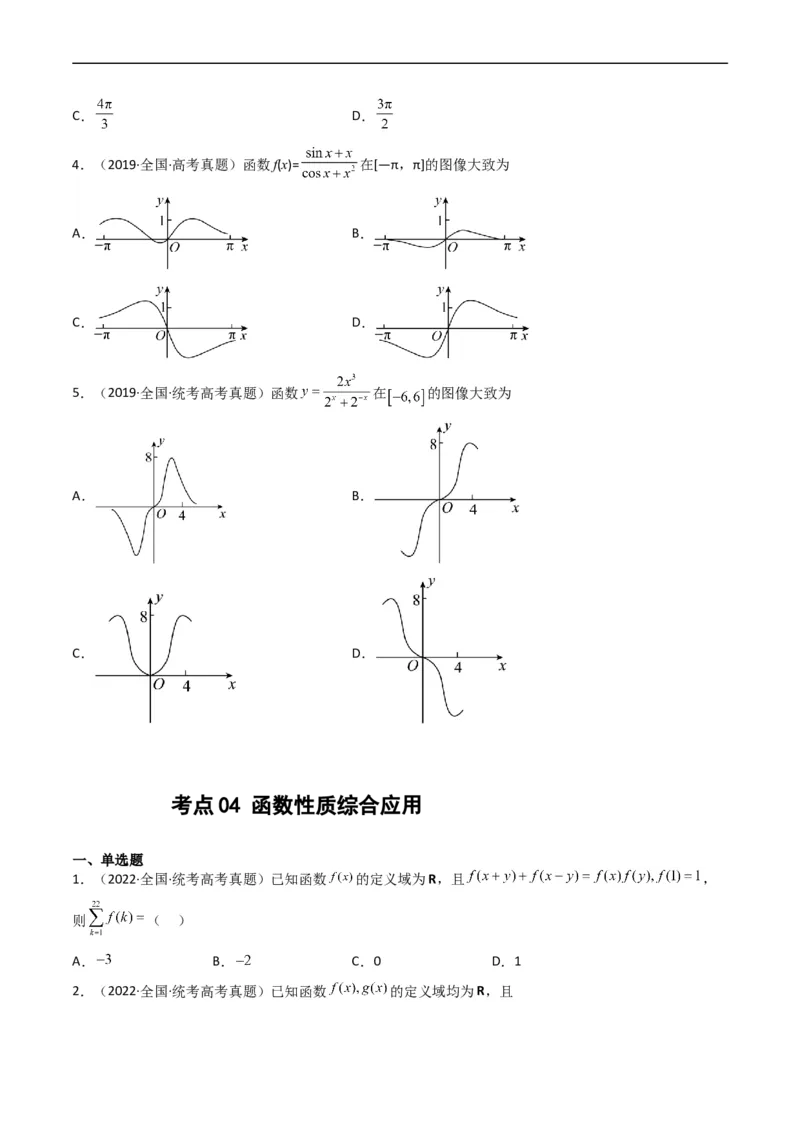
4.(2019·全国·高考真题)函数f(x)= 在[—π,π]的图像大致为
A. B.
C. D.
5.(2019·全国·统考高考真题)函数 在 的图像大致为
A. B.
C. D.
考点 04 函数性质综合应用
一、单选题
1.(2022·全国·统考高考真题)已知函数 的定义域为R,且 ,
则 ( )
A. B. C.0 D.1
2.(2022·全国·统考高考真题)已知函数 的定义域均为R,且.若 的图像关于直线 对称, ,则
( )
A. B. C. D.
3.(2021·全国·统考高考真题)设 ,若 为函数 的极大值点,则( )
A. B. C. D.
4.(2021·全国·高考真题)设 是定义域为R的奇函数,且 .若 ,则
( )
A. B. C. D.
5.(2021·全国·统考高考真题)设函数 的定义域为R, 为奇函数, 为偶函数,当
时, .若 ,则 ( )
A. B. C. D.
6.(2021·全国·统考高考真题)已知函数 的定义域为 , 为偶函数, 为奇函数,
则( )
A. B. C. D.
7.(2020·山东·统考高考真题)若定义在 的奇函数f(x)在 单调递减,且f(2)=0,则满足
的x的取值范围是( )
A. B.
C. D.
8.(2019·全国·高考真题)设函数 的定义域为R,满足 ,且当 时,
.若对任意 ,都有 ,则m的取值范围是
A. B.
C. D.