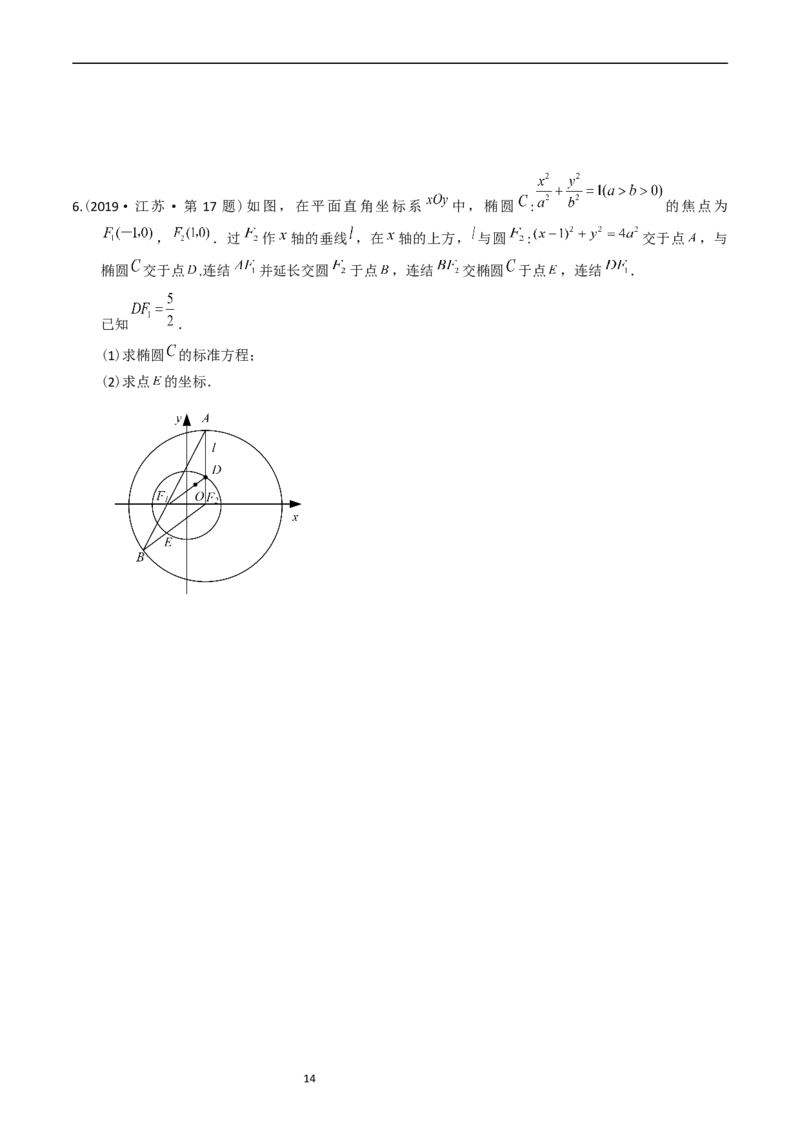文档内容
五年(2019-2023)年高考真题分项汇编
专题 08 平面解析几何(解答题)
平面解析几何在高考中考查比例较大,一般是1+1+1模式或者是2+1+1模式。在选题中,解析几何解答题
中难度一般较大,计算量比较大.主要知识点是
考点01 椭圆及其性质
考点02 双曲线及其性质
考点03 抛物线及其性质
考点04 解析几何定点定值问题
考点05 解析几何综合性问题
考点 01 椭圆及其性质
1.(2020年新高考全国卷Ⅱ数学(海南)·第21题)已知椭圆C: 过点M(2,3),点A
为其左顶点,且AM的斜率为 ,
(1)求C的方程;
(2)点N为椭圆上任意一点,求△AMN的面积的最大值.
2.(2020江苏高考·第18题)在平面直角坐标系 中,已知椭圆 的左、右焦点分别为
,点 在椭圆 上且在第一象限内, ,直线 与椭圆 相交于另一点 .
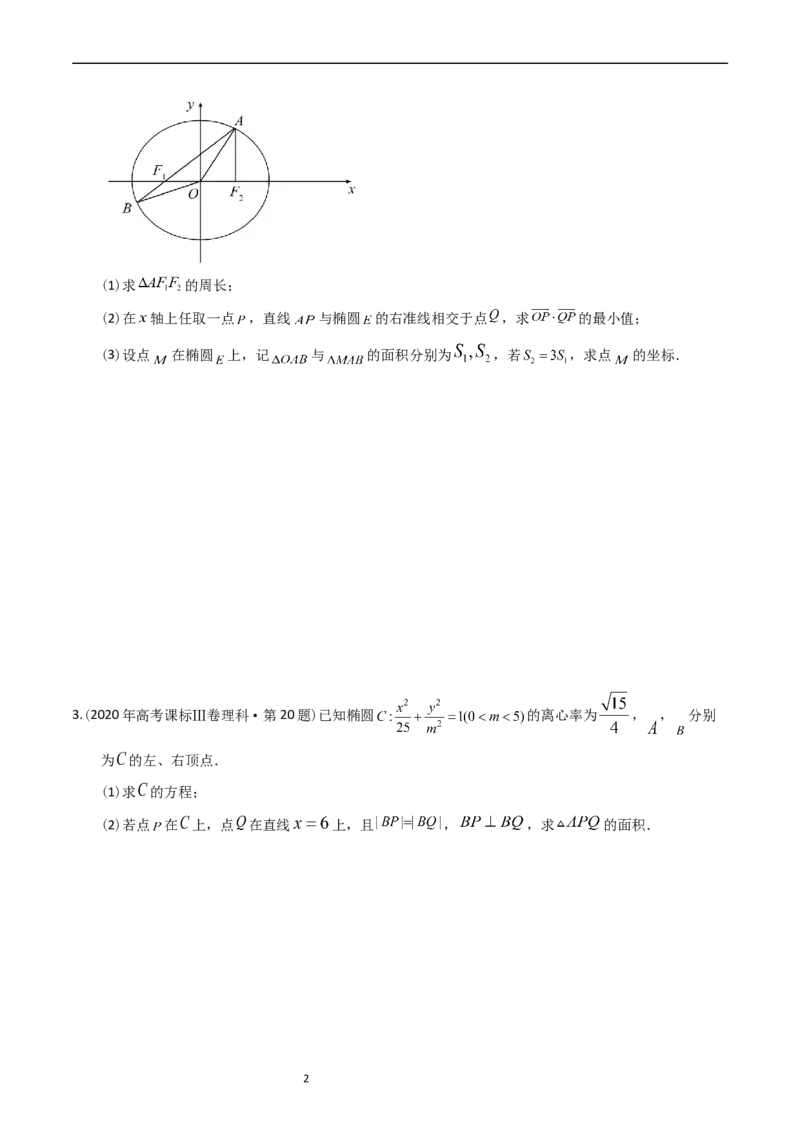
1(1)求 的周长;
(2)在 轴上任取一点 ,直线 与椭圆 的右准线相交于点 ,求 的最小值;
(3)设点 在椭圆 上,记 与 的面积分别为 ,若 ,求点 的坐标.
3.(2020年高考课标Ⅲ卷理科·第20题)已知椭圆 的离心率为 , , 分别
为 的左、右顶点.
(1)求 的方程;
(2)若点 在 上,点 在直线 上,且 , ,求 的面积.
25.(2023年北京卷·第19题)已知椭圆 离心率为 ,A、C分别是E的上、
的
下顶点,B,D分别是 的左、右顶点, .
(1)求 的方程;
(2)设 为第一象限内E上的动点,直线 与直线 交于点 ,直线 与直线 交于点
.求证: .
6.(2023年天津卷·第18题)设椭圆 的左右顶点分别为 ,右焦点为 ,已知
.
(1)求椭圆方程及其离心率;
(2)已知点 是椭圆上一动点(不与端点重合),直线 交 轴于点 ,若三角形 的面积是三角
形 面积的二倍,求直线 的方程.
7.(2022高考北京卷·第19题)已知椭圆: 的一个顶点为 ,焦距为 .
(1)求椭圆E的方程;
(2)过点 作斜率为k的直线与椭圆E交于不同的两点B,C,直线AB,AC分别与x轴交于点M,
N,当 时,求k的值.
38.(2022年浙江省高考数学试题·第21题)如图,已知椭圆 .设A,B是椭圆上异于 的两
点,且点 在线段 上,直线 分别交直线 于C,D两点.
(1)求点P到椭圆上点的距离的最大值;
(2)求 的最小值.
9 .(2021高考北京·第20题)已知椭圆 一个顶 点 ,以椭圆 的四个顶
点为顶点的四边形面积为 .
(1)求椭圆E的方程;
(2)过点P(0,-3)的直线l斜率为k的直线与椭圆E交于不同的两点B,C,直线AB,AC分别与直线交
y=-3交于点M,N,当|PM|+|PN|≤15时,求k的取值范围.
410.(2020天津高考·第18题)已知椭圆 的一个顶点为 ,右焦点为 ,且
,其中 为原点.
(Ⅰ)求椭圆 的方程;
(Ⅱ)已知点 满足 ,点 在椭圆上( 异于椭圆的顶点),直线 与以 为圆心的圆相切
于点 ,且 为线段 的中点.求直线 的方程.
11.(2019·上海·第20题)已知椭圆 , 为左、右焦点,直线 过 交椭圆于A、B两点.
(1)若AB垂直于 轴时,求 ;
(2)当 时, 在 轴上方时,求 的坐标;
(3)若直线 交 轴于M,直线 交 轴于N,是否存在直线 ,使 ,若存在,求
出直线 的方程;若不存在,请说明理由.
考点 02 双曲线及其性质
1.(2023年新课标全国Ⅱ卷·第21题)已知双曲线C的中心为坐标原点,左焦点为 ,离心率为
.
(1)求C的方程;
(2)记C 左的、右顶点分别为 , ,过点 的直线与C的左支交于M,N两点,M在第二象限,
直线 与 交于点P.证明:点 在定直线上.
52.(2022新高考全国II卷·第21题)已知双曲线 的右焦点为 ,渐近线方程
为 .
(1)求C的方程;
(2)过F的直线与C的两条渐近线分别交于A,B两点,点 在C上,且.
.过P且斜率为 的直线与过Q且斜率为 的直线交于点M.从下面①②③中
选取两个作为条件,证明另外一个成立:
①M在 上;② ;③ .
注:若选择不同的组合分别解答,则按第一个解答计分.
3.(2021年新高考Ⅰ卷·第21题)在平面直角坐标系 中,已知点 、
,点 的轨迹为 .
(1)求 的方程;
(2)设点 在直线 上,过 两条直线分别交 于 、 两点和 , 两点,且
的
,求直线 的斜率与直线 的斜率之和.
4.(2022新高考全国I卷·第21题)已知点 在双曲线 上,直线l交C于P,Q
两点,直线 的斜率之和为0.
(1)求l 的斜率;
(2)若 ,求 的面积.
6考点 03 抛物线及其性质
1.(2023年全国甲卷理科·第20题)已知直线 与抛物线 交于 两点,
且 .
(1)求 ;
(2)设F为C的焦点,M,N为C上两点, ,求 面积的最小值.
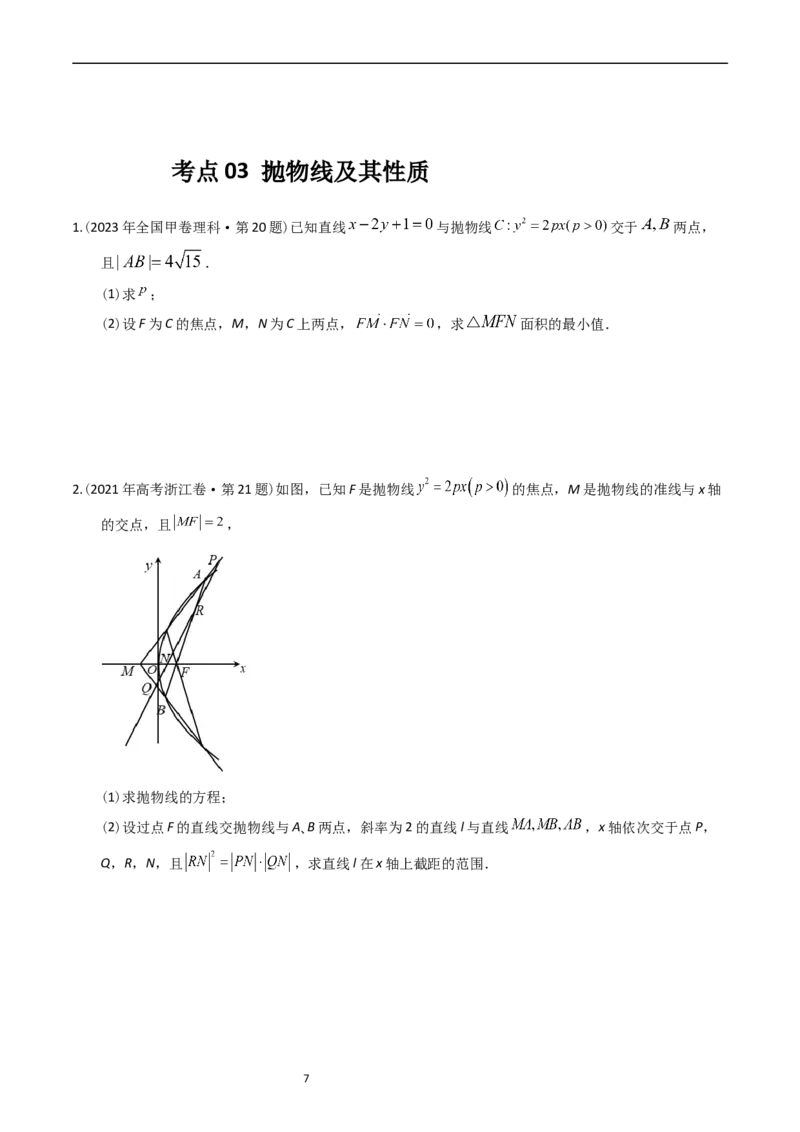
2.(2021年高考浙江卷·第21题)如图,已知F是抛物线 的焦点,M是抛物线的准线与x轴
的交点,且 ,
(1)求抛物线的方程;
(2)设过点F的直线交抛物线与A、B两点,斜率为2的直线l与直线 ,x轴依次交于点P,
Q,R,N,且 ,求直线l在x轴上截距的范围.
73.(2021年高考全国乙卷理科·第21题)已知抛物线 的焦点为 ,且 与圆
上点的距离的最小值为 .
(1)求 ;
(2)若点 在 上, 是 的两条切线, 是切点,求 面积的最大值.
4.(2021年高考全国甲卷理科·第20题)抛物线C的顶点为坐标原点O.焦点在x轴上,直线l: 交C
于P,Q两点,且 .已知点 ,且 与l相切.
(1)求C, 的方程;
(2)设 是C上的三个点,直线 , 均与 相切.判断直线 与 的位置关
系,并说明理由.
5.(2020年浙江省高考数学试卷·第21题)如图,已知椭圆 ,抛物线 ,
点A是椭圆 与抛物线 的交点,过点A的直线l交椭圆 于点B,交抛物线 于M(B,M不同于
A).
8(Ⅰ)若 ,求抛物线 的焦点坐标;
(Ⅱ)若存在不过原点的直线l使M为线段AB的中点,求p的最大值.
6.(2022年高考全国甲卷数学(理)·第20题)设抛物线 的焦点为F,点 ,过F的直
线交C于M,N两点.当直线MD垂直于x轴时, .
(1)求C的方程;
(2)设直线 与C 的另一个交点分别为A,B,记直线 的倾斜角分别为 .当 取得
最大值时,求直线AB的方程.
7.(2019·浙江·第21题)如图,已知点 为抛物线 的焦点.过点 的直线交抛物线于
, 两点,点 在抛物线上,使得 的重心 在 轴上,直线 交 轴于 点,且 在点
的右侧,记 , 的面积分别为 , .
(Ⅰ)求 的值及抛物线的准线方程;
(Ⅱ)求 的最小值及此时点 的坐标.
8.(2019·全国Ⅲ·理·第21题)已知曲线C:y= ,D为直线y= 上的动点,过D作C的两条切线,
切点分别为A,B.
(1)证明:直线AB过定点:
(2)若以E(0, )为圆心的圆与直线AB相切,且切点为线段AB的中点,求四边形ADBE的面积.
99.(2019·全国Ⅰ·理·第19题)已知抛物线 的焦点为 ,斜率为 的直线 与 的交点为 ,
,与 轴的交点为 .
(1)若 ,求 的方程;
(2)若 ,求 .
10.(2019·北京·理·第18题)已知抛物线C:x2=−2py经过点(2,−1).
(Ⅰ)求抛物线C的方程及其准线方程;
(Ⅱ)设O为原点,过抛物线C的焦点作斜率不为0的直线l交抛物线C于两点M,N,直线y=−1分别
交直线OM,ON于点A和点B.求证:以AB为直径的圆经过y轴上的两个定点.
考点 04 圆锥曲线的定点定值问题
1.(2021年新高考全国Ⅱ卷·第20题)已知椭圆C的方程为 ,右焦点为 ,且
离心率为 .
(1)求椭圆C的方程;
(2)设M,N是椭圆C上的两点,直线 与曲线 相切.证明:M,N,F三点共线的
充要条件是 .
102.(2020年高考课标Ⅰ卷理科·第20题)已知A、B分别为椭圆E: (a>1) 左、右顶点,G为E
的
的上顶点, ,P为直线x=6上的动点,PA与E的另一交点为C,PB与E的另一交点为D.
(1)求E 的方程;
(2)证明:直线CD过定点.
3.(2020年新高考全国Ⅰ卷(山东)·第22题)已知椭圆C: 的离心率为 ,且过点
A(2,1).
(1)求C的方程:
(2)点M,N在C上,且AM⊥AN,AD⊥MN,D为垂足.证明:存在定点Q,使得|DQ|为定值.
4.(2022年高考全国乙卷数学(理)·第20题)已知椭圆E的中心为坐标原点,对称轴为x轴、y轴,且过
两点.
(1)求E的方程;
(2)设过点 的直线交E于M,N两点,过M且平行于x轴的直线与线段AB交于点T,点H满
足 .证明:直线HN过定点.
考点 05 解析几何综合类问题
111.(2023年新课标全国Ⅰ卷·第22题)在直角坐标系 中,点 到 轴的距离等于点 到点 的距
离,记动点 的轨迹为 .
(1)求 的方程;
(2)已知矩形 有三个顶点在 上,证明:矩形 的周长大于 .
2 .(2023年全国乙卷理科·第20题)已知椭圆 的离心率是 ,点 在
上.
(1)求 方的程;
(2)过点 的直线交 于 两点,直线 与 轴的交点分别为 ,证明:线段
的中点为定点.
3 .(2020年高考课标Ⅱ卷理科·第19题)已知椭圆C : (a>b>0) 右焦点F与抛物线C 的焦点
1 的2
重合,C 的中心与C 的顶点重合.过F且与x轴垂直的直线交C 于A,B两点,交C 于C,D两点,
1 2 1 2
且|CD|= |AB|.
(1)求C 的离心率;
1
(2)设M是C 与C 的公共点,若|MF|=5,求C 与C 的标准方程.
1 2 1 2
124.(2019·天津·理·第18题)设椭圆 的左焦点为 ,上顶点为 .已知椭圆的短轴
长为4,离心率为 .
(Ⅰ)求椭圆的方程;
(Ⅱ)设点 在椭圆上,且异于椭圆的上、下顶点,点 为直线 与 轴的交点,点 在 轴的负
半轴上.若 ( 为原点),且 ,求直线 的斜率.
5.(2019·全国Ⅱ·理·第21题)已知点 , ,动点 满足直线 与 的斜
率之积为 .记 的轨迹为曲线 .
求 的方程,并说明 是什么曲线;
过坐标原点的直线交 于 两点,点 在第一象限, 轴,垂足为 ,连结 并延长
交 于点 .
证明: 是直角三角形;
求 面积的最大值.
136.(2019·江苏·第 17 题)如图,在平面直角坐标系 中,椭圆 : 的焦点为
, .过 作 轴的垂线 ,在 轴的上方, 与圆 : 交于点 ,与
椭圆 交于点 .连结 并延长交圆 于点 ,连结 交椭圆 于点 ,连结 .
已知 .
(1)求椭圆 的标准方程;
(2)求点 的坐标.
14