文档内容
【赢在高考·黄金8卷】备战2024年高考数学模拟卷(新高考Ⅰ卷专用)
黄金卷01
(考试时间:120分钟 试卷满分:150分)
第 I 卷(选择题)
一、单项选择题:本题共8小题,每小题5分,共40分,在每小题给出的四个选项中,只有一项是符合要
求的。
1.设集合 ,集合 ,则 ( )
A. B. C. D.
【答案】C
【解析】 ,故 .故选 .
2.已知复数z满足 ,则复数 在复平面内对应的点位于( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
【答案】D
【解析】 ,
所以复数 在复平面内对应的点位于第四象限,故选D
3.函数 的最小值为( )
A.-2 B. C. D.0
【答案】B
【解析】
当 时,取得最小值为 ,故选B
4.已知等差数列 的前5项和 ,且满足 ,则等差数列 的公差为( )
A.-3 B.-1 C.1 D.3
【答案】D【解析】 ; ,解得 , ,故选D
5.龙洗,是我国著名的文物之一,因盆内有龙纹故称龙洗,为古代皇宫盥洗用具,其盆体可以近似看作
一个圆台.现有一龙洗盆高15cm,盆口直径40cm,盆底直径20cm.现往盆内倒入水,当水深6cm时,盆
内水的体积近似为( )
A. B. C. D.
【答案】B
【解析】如图所示,画出圆台的立体图形和轴截面平面图形,并延长 与 于点 .
根据题意, , , , ,
设 ,
所以 , 解得 , ,
所以 ,故选B.
6.已知 的展开式中 的系数为80,则m的值为( )
A. B.2 C. D.1
【答案】A
【解析】 ,在 的展开式中,由 ,
令 ,得r无解,即 的展开式没有 的项;
在 的展开式中,由 ,
令 ,解得r=3,
即 的展开式中 的项的系数为 ,
又 的展开式中 的系数为80,
所以 ,解得 ,故选A.
7.在平面直角坐标系 中,双曲线 的左、右焦点分别为 ,点M是双曲
线右支上一点,且 为等边三角形,则双曲线C的离心率为( )
A. B. C. D.
【答案】A
【解析】如图示,连结 .
因为 为等边三角形,所以 .
所以 .
因为 ,所以 .
又 ,所以 ,所以 .在 中, ,所以 .
由双曲线的定义可得: ,即 ,
所以离心率 ,故选A.
8.设 , , ,则下列关系正确的是( )
A. B.
C. D.
【答案】C
【解析】记 .
因为 ,所以当 时, ,所以 在 上单调递增函数,
所以当 时, ,即 ,所以 .
记 .
因为 ,所以 在 上单调递增函数,
所以当 时, ,即 ,所以 .
所以 .记 .
因为 ,所以当 时, ,所以 在 上单调递增函数,所
以当 时, ,即 ,所以 .
所以 ,综上所述: .故选:C
二、多项选择题:本题共4小题,每小题5分,共20分,在每小题给出的四个选项中,有多项符合题目的
要求,全部选对的得5分,部分选对的得2分,有选错的得0分。
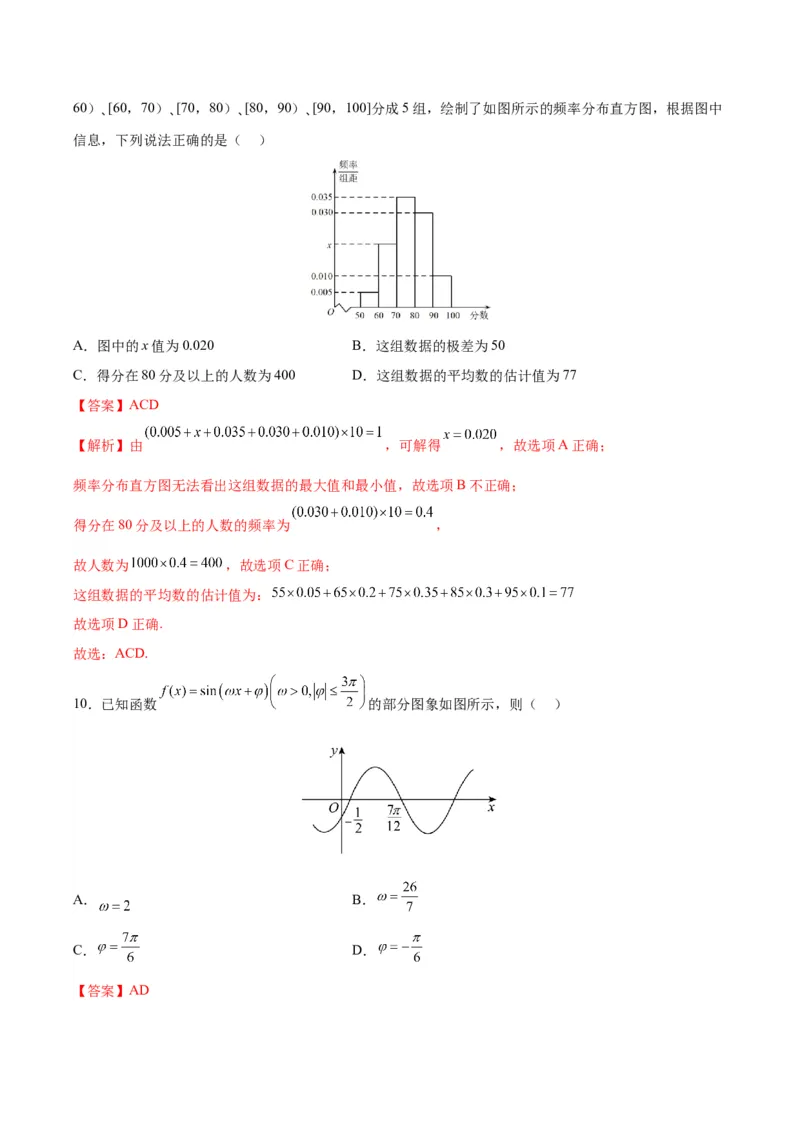
9.立德中学举行党史知识竞赛,对全校参赛的1000名学生的得分情况进行了统计,把得分数据按照[50,60)、[60,70)、[70,80)、[80,90)、[90,100]分成5组,绘制了如图所示的频率分布直方图,根据图中
信息,下列说法正确的是( )
A.图中的x值为0.020 B.这组数据的极差为50
C.得分在80分及以上的人数为400 D.这组数据的平均数的估计值为77
【答案】ACD
【解析】由 ,可解得 ,故选项A正确;
频率分布直方图无法看出这组数据的最大值和最小值,故选项B不正确;
得分在80分及以上的人数的频率为 ,
故人数为 ,故选项C正确;
这组数据的平均数的估计值为:
故选项D正确.
故选:ACD.
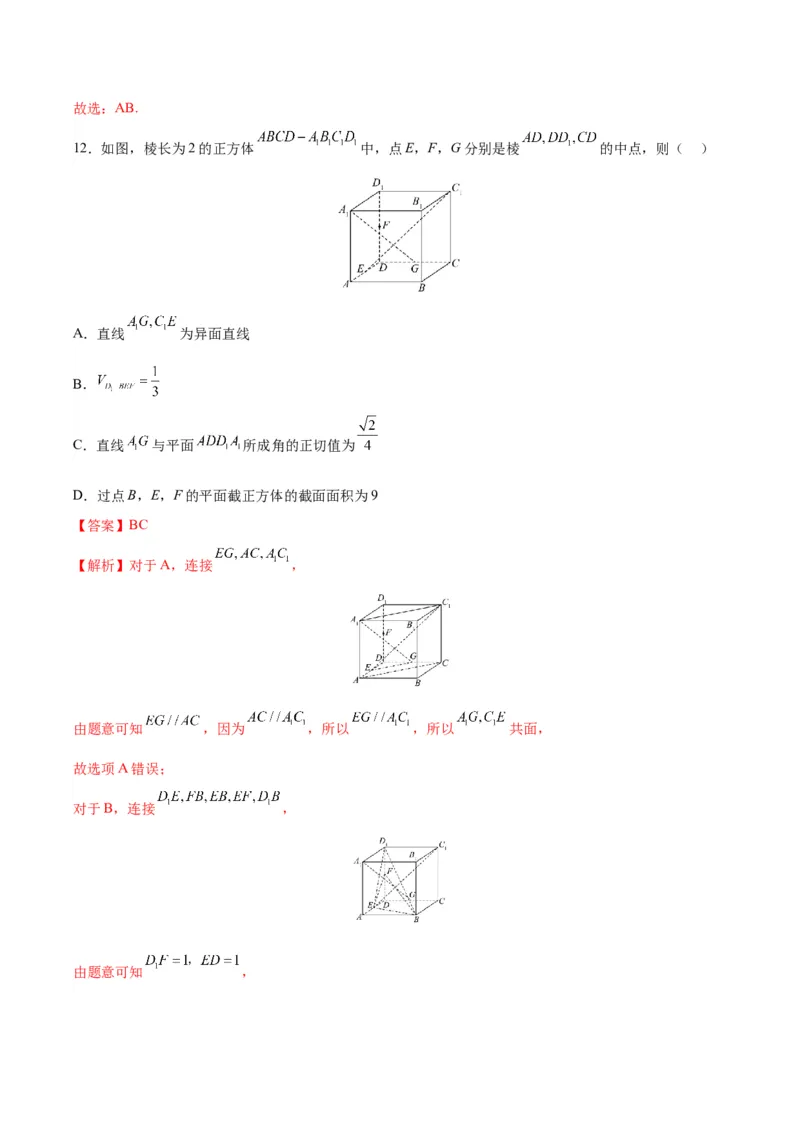
10.已知函数 的部分图象如图所示,则( )
A. B.
C. D.
【答案】AD【解析】由图可知 且 ,
,由图可知 , ,
, ,
又 ,则 ,即 ,
又由图 ,则 ,即 ,则 , .
故选:AD.
11.抛物线有如下光学性质:由其焦点射出的光线经抛物线反射后,沿平行于抛物线对称轴的方向射出.
反之,平行于抛物线对称轴的入射光线经抛物线反射后必过抛物线的焦点.已知抛物线 , 为
坐标原点,一束平行于 轴的光线 从点 射入,经过 上的点 反射后,再经过 上另一点
反射后,沿直线 射出,经过点 ,则()
A.
B.延长 交直线 于点 ,则 , , 三点共线
C.
D.若 平分 ,则
【答案】AB
【解析】由题意知,点 , ,如图:
将 代入 ,得 ,所以 ,则直线 的斜率 ,则直线 的方程为 ,即 ,
联立 ,得 ,解得 , ,
又 时, ,则
所以 ,所以A选项正确;
又 ,所以C选项错误;
又知直线 轴,且 ,则直线 的方程为 ,
又 ,所以直线 的方程为 ,
令 ,解得 ,即 , 在直线 上,
所以 , , 三点共线,所以B选项正确;
设直线 的倾斜角为 ( ),斜率为 ,直线 的倾斜角为 ,
若 平分 ,即 ,即 ,
所以 ,则 ,且 ,解得 ,
又 ,解得: ,所以D选项错误;故选:AB.
12.如图,棱长为2的正方体 中,点E,F,G分别是棱 的中点,则( )
A.直线 为异面直线
B.
C.直线 与平面 所成角的正切值为
D.过点B,E,F的平面截正方体的截面面积为9
【答案】BC
【解析】对于A,连接 ,
由题意可知 ,因为 ,所以 ,所以 共面,
故选项A错误;
对于B,连接 ,
由题意可知 ,所以 ,故选项B正确;
对于C,连接 ,
由正方体的性质可知 平面 ,所以 即为直线 与平面 所成的角,则
,故选项C正确;
对于D,连接 ,
根据正方体的性质可得 ,且 ,
所以平面 即为过点B,E,F的平面截正方体的截面,该四边形为梯形,其上底 ,下底为 ,
高为 ,所以截面面积为 ,故选项D错误;
故选:BC
第 II 卷(非选择题)
三、填空题:本题共4小题,每小题5分,共20分。
13.已知平面向量 , ,若 与 共线,则 .【答案】
【解析】 , ,则 ,
,故 ,解得
14.六个身高不同的人排成二排三列,每一列后面的那个人比他(她)前面的那个人高,则共有
种排法.
【答案】90
【解析】由于六个身高不同的人排成二排三列,每一列后面的那个人比他(她)前面的那个人高,则排法
有 种.
15.已知函数 且 的图象过定点A,且点A在直线 上,则
的最小值是 .
【答案】
【解析】函数 且 的图象过定点 ,
则 ,所以 ,
由 ,得 ,
则
令 ,则 ,
则,
当且仅当 ,即 ,即 时,取等号,
所以 的最小值是 .
16.如图,已知抛物线C: ,圆E: ,直线OA,OB分别交抛物线于A,B两点,
且直线OA与直线OB的斜率之积等于 ,则直线AB被圆E所截的弦长最小值为 .
【答案】
【解析】设 , ,设 : ,又 ,∴ ,
∴ ,∴ .
∴ ,∴ ,
∴直线AB恒过点 ,
由图结合圆的弦长公式可知,当圆心E到动直线AB的距离最大时,即当直线 时,弦长最短,此时弦 最小为 .
四、解答题:本题共6小题,共70分,解答应写出必要的文字说明、证明过程及验算步骤。
17.(本题满分10分)在① ,② 中任选一个作为已知条件,补充在下
列问题中,并作答.
问题:在 中,角A,B,C所对的边分别为a,b,c,已知______.
(1)求B;
(2)若 的外接圆半径为2,且 ,求ac.
注:若选择不同的条件分别解答,则按第一个解答计分.
【解析】(1)选择条件①:
因为 ,在 中,由余弦定理可得 ,
即 ,则 ,
因为 ,所以 .
选择条件②:
因为 ,在 中,由正弦定理可得 ,
即 ,则 ,
因为 ,所以 ,则 ,
因为 ,所以 .
(2)因为 ,所以 ,则 ,即 ,又 ,
所以 .因为 的外接圆半径 ,
所以由正弦定理可得 ,所以 .
18.(本题满分12分)已知数列 , 满足 , , .
(1)证明: 是等比数列;
(2)求数列 的前 项和 .
【解析】(1)依题意, .
又 .
故 为首项 ,公比 的等比数列.
(2)由(1)可知 .
所以 .
①
②
①-②得
,
故 .
19.(本题满分12分)某市航空公司为了解每年航班正点率 对每年顾客投诉次数 (单位:次)的影
响,对近8年(2015年~2022年)每年航班正点率 和每年顾客投诉次数 的数据作了初步处理,得到下面的一些统计量的值.
(1)求 关于 的经验回归方程;
(2)该市航空公司预计2024年航班正点率为 ,利用(1)中的回归方程,估算2024年顾客对该市航空
公司投诉的次数;
(3)根据数据统计,该市所有顾客选择乘坐该航空公司航班的概率为 ,现从该市所有顾客中随机抽取4人,
记这4人中选择乘坐该航空公司航班的人数为 ,求 的分布列和数学期望.
附:经验回归直线 的斜率和截距的最小二乘法估计公式分别为:
【解析】(1) ,
则 ,
所以 ,
所以 ;
(2)当 时, ,
所以2024年顾客对该市航空公司投诉的次数为 次;
(3) 可取 ,
, ,
, ,,
所以分布列为
所以 .
20.(本题满分12分)如图所示,在梯形ABCD中, , ,四边形ACFE为矩形,且
平面ABCD, .
(1)求证: 平面BCF;
(2)点M在线段EF上运动,当点M在什么位置时,平面MAB与平面FCB所成的锐二面角为 .
【解析】(1)证明:设 ,在梯形 中,过 分别作 的垂线,垂足分别为 ,
∵ , ,所以 ,
∴ ,∴ ,
∴ ,则 .
∵ 平面ABCD, 平面ABCD,∴ ,而 ,CF, 平面BCF,
∴ 平面BCF.∵ ,∴ 平面BCF.
(2)以C为坐标原点,分别以直线CA,CB,CF为x轴、y轴、z轴建立如图所示的空间直角坐标系,设
,
则 , , , ,
∴ , .
设 为平面MAB的法向量,
由 得 取 ,则
易知 是平面FCB的一个法向量,
∴ ,
∵ ,∴当 时,
即 与 重合时,平面MAB与平面FCB所成的锐二面角为 .
21.(本题满分12分)已知椭圆 经过点 ,左顶点为 ,右焦点为 ,
已知点 ,且 , , 三点共线.
(1)求椭圆 的方程;(2)已知经过点 的直线l与椭圆 交于 , 两点,过点 作直线 的垂线,垂足为 ,求证:直线
过定点.
【解析】(1)解:由题意,将点 代入椭圆的方程,可得 ,
又由 是 轴上一点,且 三点共线,
可得所以 ,解得 ,
代入 ,可得 ,所以椭圆 的方程为 .
(2)解:当 时,此时直线 的方程为 ,
联立方程组 ,解得 或 ,可得 ,
此时 ,直线 的方程为 ,
当 时,同理可得 ,此时 ,
可得直线 的方程为 ,
由 ,解得 ,即两直线的交点为 ,
下面证明直线 经过 轴上定点 .
设直线 的方程为 ,
联立方程组 ,整理得 ,设 ,则 ,
所以直线 的方程: .
令 ,可得
.
因为 ,
所以 .
所以直线 过定点 .
22.(本题满分12分)已知函数 ( , )
(1)讨论函数 的单调性;
(2)若关于x的不等式 恒成立,求实数m的取值范围.
【解析】(1)因为 ,其定义域为
所以 .
当 ,即 时, ,所以 在 上单调递增;
当 ,即 时,由 得: ,所以 在 上单调递增;
得: ,所以 在 上单调递减;综上,当 时, 在 上单调递增;
当 时, 在 上单调递增,在 上单调递减;
(2)因为 , ,
所以 ,所以 在 上恒成立.
令 ,则 ,
令 ,则 ,
所以 在 上单调递增.
又 , ,所以 在 上有唯一零点 ,使 .
即 ,即 ,即 ,
当 时, ,当 时, ,
所以 在 处取得极小值,也是最小值.
令 , ,当 时, 恒成立,
所以函数 在 上单调递增,所以 ,即 ,即 .
所以 的最小值 ,
所以 ,即 ,所以实数m的取值范围是 .