文档内容
【赢在高考·黄金8卷】备战2024年高考数学模拟卷(全国卷专用)
黄金卷01(文科)
(考试时间:120分钟 试卷满分:150分)
第 I 卷(选择题)
一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题
目要求的.
1.已知全集 ,集合 , ,则 ( )
A. B. C. D.
2.在 中,点 分别对应复数 ,则点 对应复数的共轭复数是( )
A. B.
C. D.
3.已知函数 ( 且 ),则其大致图象为( )
A. B.
C. D.
4.连续抛掷一枚质地均匀的骰子两次,分别标记两次骰子正面朝上的点数,则事件“两次正面朝上的点
数之积大于8”的概率为( )
A. B. C. D.
5.我国古代数学名著《数书九章》中有“天池盆测雨”题:在下雨时,用一个圆台形的天池盆接雨水,
天池盆盆口直径为二尺八寸,盆底直径为一尺二寸,盆深一尺八寸,若盆中积水深九寸,则平地降雨量是
(注:①平地降雨量等于盆中积水体积除以盆口面积;②一尺等于十寸)( )A.6寸 B.4寸 C.3寸 D.2寸
6.已知角 的始边为 轴的非负半轴,终边经过点 ,则 ( )
A.2 B. C. 或2 D.
7.已知命题p:对任意实数都有 恒成立,命题q:关于x的方程 有实数根.若
为真命题,则实数a的取值范围是( )
A. B. C. D.
8.设抛物线 的焦点为 ,直线 过点 与抛物线 交于 两点,以 为直径的圆与 轴交
于 两点,且 ,则直线 的方程为( )
A. B. C. D.
9.已知 ,给出下列结论:
若 , ,且 ,则 ;
存在 ,使得 的图象向左平移 个单位长度后得到的图象关于 轴对称;
若 ,则 在 上单调递增;
若 在 上恰有 个零点,则 的取值范围为 .
其中,所有正确结论的个数是( )
A. B. C. D.
10.在平面四边形 中, ,则 的最大值为( )
A. B.C.12 D.15
11.设 是一个无穷数列 的前 项和,若一个数列满足对任意的正整数 ,不等式 恒成立,
则称数列 为和谐数列,判断下列2个命题的真假:( )
①若等差数列 是和谐数列,则 一定存在最小值;
②若 的首项小于零,则一定存在公比为负数的一个等比数列是和谐数列.
A.①假命题,②真命题 B.①假命题,②假命题
C.①真命题,②假命题 D.①真命题,②真命题
12.设函数 , , 在 上的零点分别为 ,则
的大小顺序为( )
A. B. C. D.
第 II 卷(非选择题)
二、填空题:本大题共4小题,每小题5分,共20分
13.已知 是夹角为60°的两个单位向量,则 与 的夹角是 .
14.将边长为2的等边 沿 边中线 折起得到三棱锥 ,当所得三棱锥体积最大时,点
到平面 的距离为 .
15.已知 的内角 , , 所对的边分别为 , , ,若 , ,
且 ,则 .
16.已知函数 的定义域均为 , 是偶函数, 是奇函数,且,则 ; .
三、解答题:本大题共70分.解答应写出文字说明、证明过程或演算步骤.第17~21题为必考题,每个试
题考生都必须作答.第22、23题为选考题,考生根据要求作答.
(一)必考题:共60分.
17.(12分)已知数列 的前 项和为 ,且满足 , ,当 时, 是4的常数
列.
(1)求 的通项公式;
(2)当 时,设数列 的前 项和为 ,证明: .
18.(12分)第三十一届世界大学生夏季运动会于2023年8月8日晚在四川省成都市胜利闭幕.来自113
个国家和地区的6500名运动员在此届运动会上展现了青春力量,绽放青春光彩,以饱满的热情和优异的状
态谱写了青春、团结、友谊的新篇章.外国运动员在返家时纷纷购买纪念品,尤其对中国的唐装颇感兴趣.
现随机对200名外国运动员(其中男性120名,女性80名)就是否有兴趣购买唐装进行了解,统计结果如
下:
无兴
有兴趣 合计
趣
男性运动员 80 40 120
女性运动员 40 40 80
合计 120 80 200
(1)是否有99%的把握认为“外国运动员对唐装感兴趣与性别有关”;
(2)按分层抽样的方法抽取6名对唐装有兴趣的运动员,再从中任意抽取2名运动员作进一步采访,求抽取
的两名运动员恰好是一名男性和一名女性的概率.参考公式:
临界值表:
0.150 0.100 0.050 0.025 0.010 0.001
2.072 2.706 3.841 5.024 6.635 10.828
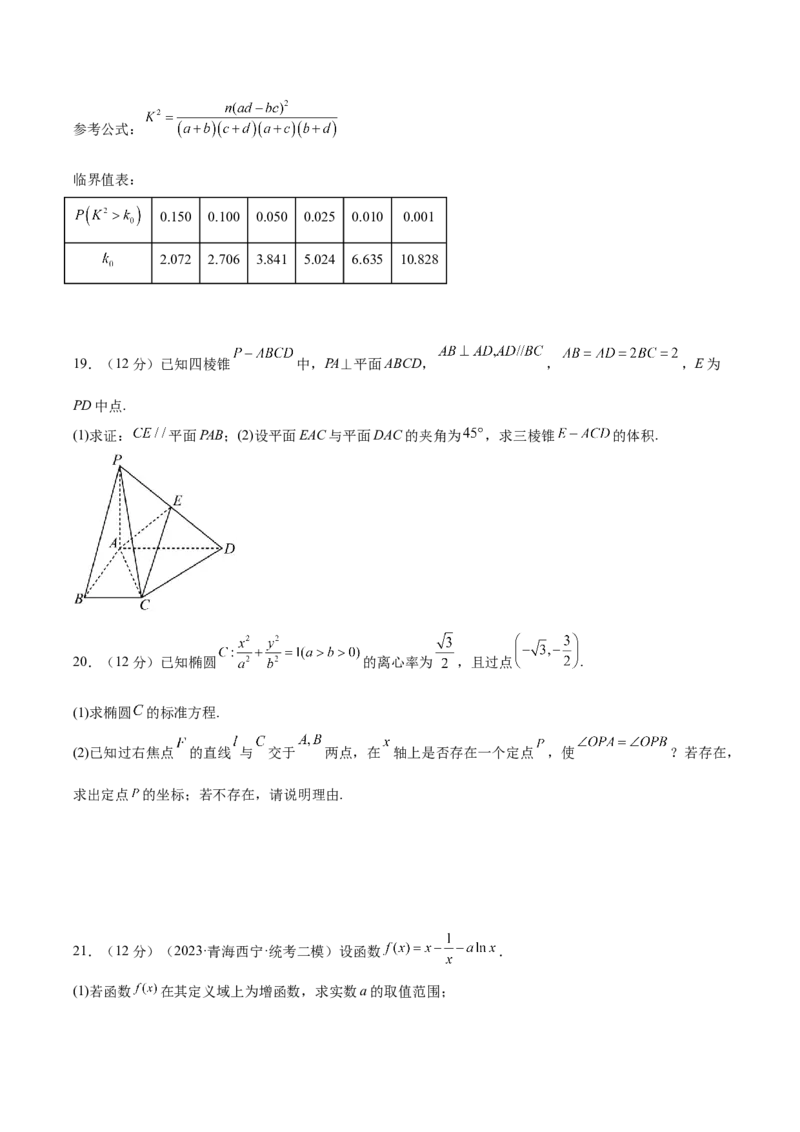
19.(12分)已知四棱锥 中,PA⊥平面ABCD, , ,E为
PD中点.
(1)求证: 平面PAB;(2)设平面EAC与平面DAC的夹角为 ,求三棱锥 的体积.
20.(12分)已知椭圆 的离心率为 ,且过点 .
(1)求椭圆 的标准方程.
(2)已知过右焦点 的直线 与 交于 两点,在 轴上是否存在一个定点 ,使 ?若存在,
求出定点 的坐标;若不存在,请说明理由.
21.(12分)(2023·青海西宁·统考二模)设函数 .
(1)若函数 在其定义域上为增函数,求实数a的取值范围;(2)当 时,设函数 ,若在[ 上存在 , 使 成立,求实数a的取值范
围.
(二)选考题:共10分.请考生在22、23题中任选一题作答,如果多做,则按所做的第一题计分.
选修4-4:坐标系与参数方程
22.(10分)已知曲线 的参数方程分别为 ( 为参数), ( 为参
数).
(1)将 的参数方程化为普通方程;
(2)以坐标原点 为极点,以 轴的非负半轴为极轴,建立极坐标系.若射线 与曲线 分别
交于 两点(异于极点),点 ,求 的面积.
选修4-5:不等式选讲
23.(10分)已知a、b均为正数,设 .
(1)当 时,求不等式 的解集;
(2)若 的最小值为6,求 的值,并求 的最小值.