2024届福建省厦门市高三下学期第四次质量检测考试数学试题+答案(1)_2024年5月_025月合集_2024届福建省厦门市高三下学期联考模拟预测

{#{QQABCYQAgggAQJIAARgCQQFQCgMQkBGAACoOwBAMMAIACQNABCA=}#}{#{QQABCYQAgggAQJIAARgCQQFQCgMQkBGAACoOwBAMMAIACQNABCA=}#}{#{QQABCYQAgggAQJIAARgCQQFQCgMQkBGAACoOwBAMMAIACQNABCA=}#}{#{QQABCYQAgggAQJIAARgCQQFQCgMQkBGAACoOwBAMMAIACQNABCA=}#}厦门市 2024 届高中毕业班第四次质量检查 一、单选题 1-4．ACAC 5-8．CBDB 二、多选题 9．AD 10．ABD 11．ACD 三、填空题 π π 12．2 3； 13．(−,−1) (1,+)； 14．( , ); 6 2 四、解答题 S  15．设S 为数列a 的前n项和，已知a =2,S =10，且 n为等差数列． n n 2 4  n  （1）求数列a 为通项公式； n a ,n为奇数,  n （2）若数列b 满足b = 1 求数列b 的前2n项和T ． n n ，n为偶数, n 2n  a a n n+2 S  解析：（1）设等差数列 n的公差为d ，因为a =S =1，  n  1 1 S S 10 1 所以 4 − 1 =3d ，即 −1=3d ，d = ， ....................................................... 2分 4 1 4 2 S 1 n(n+1) 所以 n =1+ (n−1)，即S = ，............................................................. 3分 n 2 n 2 n(n+1) n(n−1) 当n≥2时，a =S −S = − =n， ............................................ 5分 n n n−1 2 2 当n=1时，a =1，满足上式， 1 所以a =n． .......................................................................................................... 6分 n n,n为奇数,  （2）由（1）知b = 1 ........................................................... 7分 n ，n为偶数,  n(n+2) 则T =(b +b +b +b )+(b +b +b +b ) ............................................... 8分 2n 1 3 5 2n−1 2 4 6 2n 1 1 1 1 =(1+3+5 +2n−1)+( + + + ) ............................. 9分 24 46 68 2n(2n+2) n(1+2n−1) 1 1 1 1 1 1 1 = + ( − + − + + − ) ........................................... 11分 2 2 2 4 4 6 2n 2n+2 1 1 =n2+ − ....................................................................................................... 13分 4 4n+4 1 1 所以数列b 的前2n项和为T =n2+ − ． n 2n 4 4n+4 16．（15分） 某地区为了解居民体育锻炼达标情况与性别之间的关系，随机调查了600位居 民，得到如下数据： 不达标 达标 合计 男 300 女 100 300 {#{QQABCYQAgggAQJIAARgCQQFQCgMQkBGAACoOwBAMMAIACQNABCA=}#}合计 450 600 （1）完成22列联表．根据小概率值=0.01的独立性检验，能否认为体育锻炼 达标与性别有关联？ 4 （2）若体育锻炼达标的居民体能测试合格的概率为 ，体育锻炼未达标的居民体 5 2 能测试合格的概率为 ，以频率估计概率，从该地区居民中随机抽取3人参加体能测 5 试，求3人中合格的人数X 的分布列及期望． n(ad−bc)2 （x 对应值见下表．2 = ，n=a+b+c+d)  (a+b)(a+c)(c+d)(b+d)  0．1 0．05 0．01 x 2．706 3．841 6．635  方法一：（1）22列联表如下表： 不达标 达标 合计 男 50 250 300 女 100 200 300 合计 150 450 600 ...................................................................................................................................... 1分 零假设为 H ：体育锻炼达标与性别独立，即体育锻炼达标与性别无关． ......................... 2分 0 600(50200−250100)2 200 2 = = 22.2226.635 ..................................... 5分 300300150450 9 根据小概率值=0.01的独立性检验，推断H 不成立，即认为体育锻炼达标与性别有 0 关联，该推断犯错误的概率不超过0.01． ...................................................................... 6分 （2）设事件A=“随机抽取一人体育锻炼达标”，事件B=“随机抽取一人体能测试合 3 1 4 2 格”，则P(A)= ，P(B)= ，P(B|A)= ，P(B|A)= ..................................... 8分 4 4 5 5 7 所以P(B)=P(A)P(B|A)+P(A)P(B|A)= .................................................. 10分 10 X 的可能取值为：0，1，2，3 ..................................................................... 11分 3 27 P(X =0)=( )3 = 10 1000 3 7 189 P(X =1)=C1( )2( )= ........................................................................... 12分 3 10 10 1000 3 7 441 P(X =2)=C2( )( )2 = 3 10 10 1000 7 343 P(X =3)=( )3 = ...................................................................................... 13分 10 1000 所以X 的分布列为 X 0 1 2 3 {#{QQABCYQAgggAQJIAARgCQQFQCgMQkBGAACoOwBAMMAIACQNABCA=}#}27 189 441 343 P 1000 1000 1000 1000 27 189 441 343 所以E(X)=0 +1 +2 +3 =2.1． ............................ 15分 1000 1000 1000 1000 方法二：（1）同方法一 （2）设事件A=“随机抽取一人体育锻炼达标”，事件B=“随机抽取一人体能测试合 3 1 4 2 格”，则P(A)= ，P(B)= ，P(B|A)= ，P(B|A)= ..................................... 8分 4 4 5 5 7 所以P(B)=P(A)P(B|A)+P(A)P(B|A)= .................................................. 10分 10 7 因为X B(3, ) ................................................................................................. 12分 10 3 7 所以P(X =k)=Ck( )3−k( )k,k =0,1,2,3 ....................................................... 14分 3 10 10 7 所以E(X)=3 =2.1． .................................................................................. 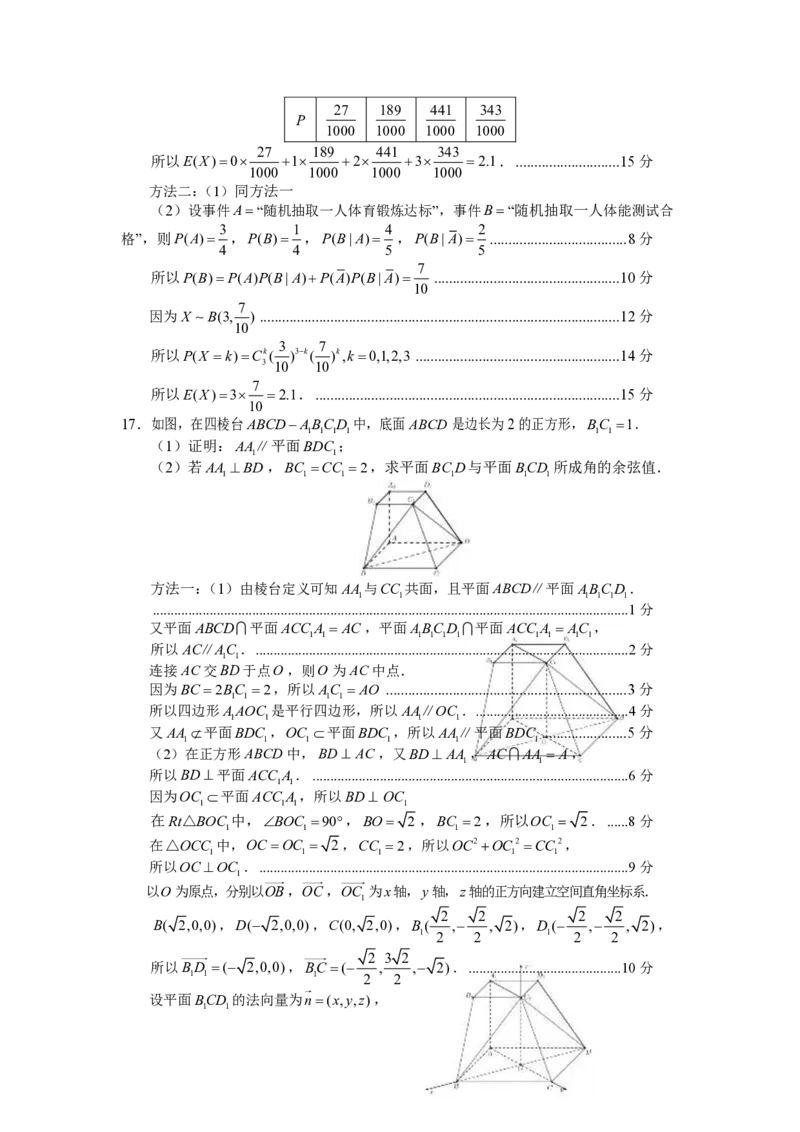15分 10 17．如图，在四棱台ABCD−ABCD 中，底面ABCD是边长为2的正方形，BC =1． 1 1 1 1 1 1 （1）证明：AA∥平面BDC ； 1 1 （2）若AA ⊥BD，BC =CC =2，求平面BCD与平面BCD 所成角的余弦值． 1 1 1 1 1 1 方法一：（1）由棱台定义可知AA与CC 共面，且平面ABCD∥平面ABCD ． 1 1 1 1 1 1 ...................................................................................................................................... 1分 又平面ABCD 平面ACC A = AC ，平面ABCD 平面ACC A = AC ， 1 1 1 1 1 1 1 1 1 1 所以AC∥AC ． ......................................................................................................... 2分 1 1 连接AC交BD于点O，则O为AC中点． 因为BC=2BC =2，所以AC = AO ................................................................. 3分 1 1 1 1 所以四边形AAOC 是平行四边形，所以AA∥OC ． ........................................... 4分 1 1 1 1 又AA 平面BDC ，OC 平面BDC ，所以AA∥平面BDC ....................... 5分 1 1 1 1 1 1 （2）在正方形ABCD中，BD⊥ AC ，又BD⊥ AA ，AC AA = A， 1 1 所以BD⊥平面ACC A． ......................................................................................... 6分 1 1 因为OC 平面ACC A，所以BD⊥ OC 1 1 1 1 在Rt△BOC 中，BOC =90，BO= 2 ，BC =2，所以OC = 2． ...... 8分 1 1 1 1 在△OCC 中，OC =OC = 2，CC =2，所以OC2+OC2 =CC2， 1 1 1 1 1 所以OC⊥OC ． ........................................................................................................ 9分 1 以O为原点，分别以OB，OC，OC 为x轴，y轴，z轴的正方向建立空间直角坐标系． 1 2 2 2 2 B( 2,0,0)，D(− 2,0,0)，C(0, 2,0)，B( ,− , 2)，D(− ,− , 2)， 1 2 2 1 2 2 2 3 2 所以BD =(− 2,0,0)，BC=(− , ,− 2)． ........................................... 10分 1 1 1 2 2 设平面BCD 的法向量为n=(x,y,z)， 1 1 {#{QQABCYQAgggAQJIAARgCQQFQCgMQkBGAACoOwBAMMAIACQNABCA=}#} nBD =0 x=0 则 1 1 ，即 ， nBC =0 3y−2z=0 1 令y=2，则z=3，所以n=(0,2,3)， .................................................................. 12分 又因为平面BCD的法向量m=(0,1,0)， .............................................................. 13分 1 mn 2 13 所以cos m,n = = ， |m||n| 13 2 13 所以平面BCD与平面BCD 所成角余弦值为 ． ....................................... 15分 1 1 1 13 方法二：（1）将棱台补形成棱锥P−ABCD， 由棱台定义知平面ABCD∥平面ABCD ． ........................................................... 1分 1 1 1 1 又平面ABCD 平面BCCB =BC ，平面ABCD 平面BCCB =BC ， 1 1 1 1 1 1 1 1 1 1 所以BC∥BC ． ......................................................................................................... 2分 1 1 连接AC交BD于点O，则O为AC中点． BC PC 又△BCP∽△BCP，所以 = =2，所以C 为PC中点， ..................... 3分 1 1 BC PC 1 1 1 1 所以OC 为△ACP的中位线，所以AA∥OC ． .................................................... 4分 1 1 1 又AA 平面BDC ，OC 平面BDC ，所以AA∥平面BDC ....................... 5分 1 1 1 1 1 1 （2）在正方形ABCD中，BD⊥ AC ，又BD⊥ AA ，AC AA = A， 1 1 所以BD⊥平面ACC A． ......................................................................................... 6分 1 1 因为OC 平面ACC A，所以BD⊥ OC 1 1 1 1 在Rt△BOC 中，BOC =90，BO= 2 ，BC =2，所以OC = 2． ...... 8分 1 1 1 1 在△OCC 中，OC =OC = 2，CC =2，所以OC2+OC2 =CC2， 1 1 1 1 1 所以OC⊥OC ． ........................................................................................................ 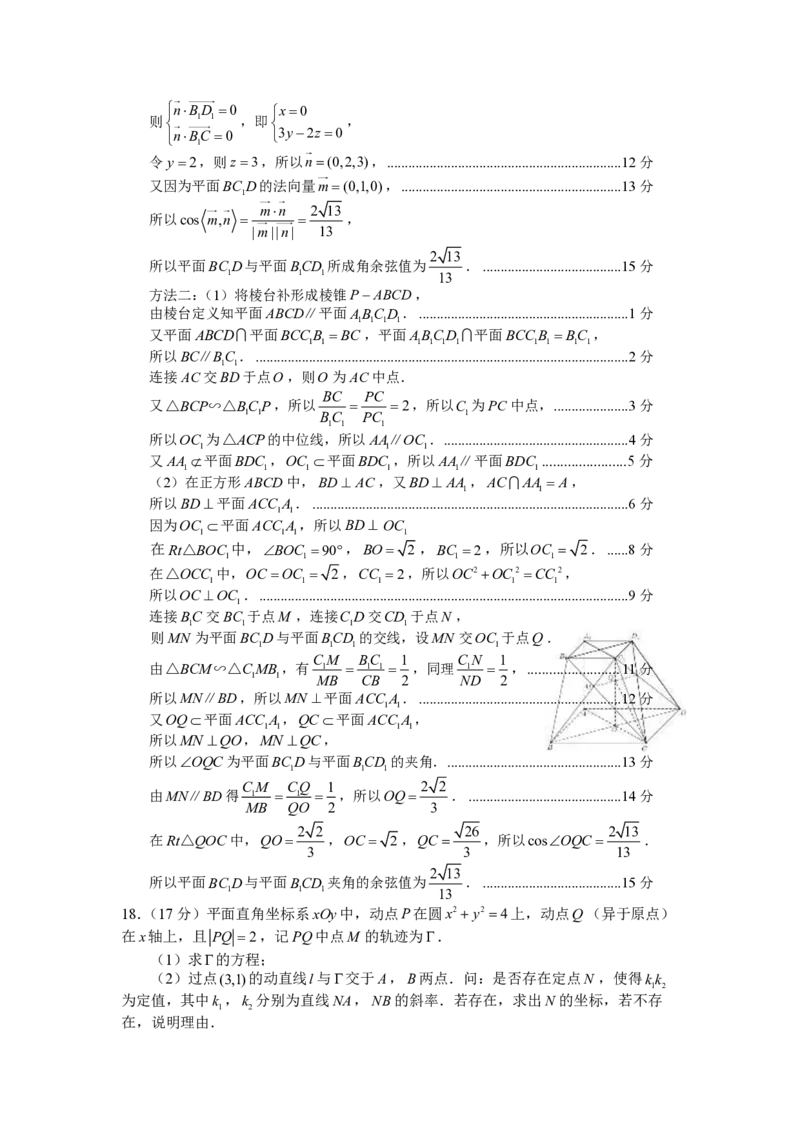9分 1 连接BC 交BC 于点M ，连接CD交CD 于点N ， 1 1 1 1 则MN 为平面BCD与平面BCD 的交线，设MN 交OC 于点Q． 1 1 1 1 CM BC 1 C N 1 由△BCM∽△CMB ，有 1 = 1 1 = ，同理 1 = ， ......................... 11分 1 1 MB CB 2 ND 2 所以MN∥BD，所以MN ⊥平面ACC A． ......................................................... 12分 1 1 又OQ平面ACC A，QC平面ACC A， 1 1 1 1 所以MN ⊥QO，MN ⊥QC， 所以OQC为平面BCD与平面BCD 的夹角． ................................................. 13分 1 1 1 CM CQ 1 2 2 由MN∥BD得 1 = 1 = ，所以OQ= ． ........................................... 14分 MB QO 2 3 2 2 26 2 13 在Rt△QOC中，QO= ，OC= 2，QC = ，所以cosOQC = ． 3 3 13 2 13 所以平面BCD与平面BCD 夹角的余弦值为 ． ....................................... 15分 1 1 1 13 18．（17分）平面直角坐标系xOy中，动点P在圆x2+ y2 =4上，动点Q（异于原点） 在x轴上，且 PQ =2，记PQ中点M 的轨迹为． （1）求的方程； （2）过点(3,1)的动直线l与交于A，B两点．问：是否存在定点N ，使得kk 1 2 为定值，其中k ，k 分别为直线NA，NB的斜率．若存在，求出N 的坐标，若不存 1 2 在，说明理由． {#{QQABCYQAgggAQJIAARgCQQFQCgMQkBGAACoOwBAMMAIACQNABCA=}#}解：（1）设点P(x,y)，M(x,y)， 因为 OP = PQ ，所以Q(2x,0)，(x0)， .......................................................... 2分  x+2x x=  2x   2 x= 由M 为PQ中点得  3 ， ....................................................... 4分 y  y=  y=2y  2 x2 代入x2+y2 =4，得 + y2 =1． .......................................................................... 5分 9 x2 所以动点M 的轨迹的方程为 +y2 =1(x0)． ............................................... 6分 9 （2）存在N 满足题意，证明如下： ........................................................................ 7分 依题意直线l的斜率存在且不为0，设l的方程：y=k(x−3)+1． 设A(x,y )，B(x ,y )，N(x ,y ) 1 1 2 2 0 0 y=k(x−3)+1  联立 x2 得(1+9k2)x2+18k(1−3k)x+81k2−54k =0． .................... 8分  + y2 =1  9 18k(1−3k) 81k2−54k 则x +x =− ,xx = （1） 1 2 1+9k2 1 2 1+9k2 y−1 直线l方程化为x=3+ ． k  y−1 x=3+   k 联立 ，得(1+9k2)y2+(6k−2)y−6k+1=0 ...................................... 9分 x2  + y2 =1  9 6k−2 1−6k 则y + y =− ,y y = （2） 1 2 1+9k2 1 2 1+9k2 6k−2 1−6k y2+ y + y −y y −y 0 1+9k2 0 1+9k2 依题意：kk = 0 1 0 2 = ...................... 10分 1 2 x −x x −x 18k(1−3k) 81k2−54k 0 1 0 2 x2+ x + 0 1+9k2 0 1+9k2 (1+9k2)y2+(6k−2)y +1−6k 9y2k2+6(y −1)k+(y −1)2 = 0 0 = 0 0 0 ........ 12分 (1+9k2)x2+18k(1−3k)x +81k2−54k 9(x −3)2k2+18(x −3)k+x2 0 0 0 0 0 依题意直线NA，NB与坐标轴不平行，又kk 为定值， 1 2 y2 y −1 (y −1)2 所以 0 = 0 = 0 ． .................................................................... 14分 (x −3)2 3(x −3) x2 0 0 0 y2 y −1 由 0 = 0 3y2 =(x −3)(y −1)．．．．．．．(3) (x −3)2 3(x −3) 0 0 0 0 0 y −1 (y −1)2 0 = 0 x2 =3(x −3)(y −1)．．．．．．．(4) 3(x −3) x2 0 0 0 0 0 由(3)（4）得x =3y 或x =−3y ， 0 0 0 0  3  3 2  3 2   x 0 = 2  x 0 = 2  x 0 =− 2 代入（3）得 或 或 ． y = 1  y =− 2  y = 2  0 2   0 2   0 2 {#{QQABCYQAgggAQJIAARgCQQFQCgMQkBGAACoOwBAMMAIACQNABCA=}#}3 1 3 2 2 3 2 2 所以N( , )或N( ,− )或N(− , )满足题意．（答案不全扣1分）17分 2 2 2 2 2 2 方法二：存在N 满足题意，证明如下： .................................................................. 7分 依题意直线l的斜率存在且不为0，设l的方程：y=k(x−3)+1． 设A(x,y )，B(x ,y )，N(x ,y ) 1 1 2 2 0 0 y=k(x−3)+1  联立 x2 得(1+9k2)x2+18k(1−3k)x+81k2−54k =0． .................... 8分  + y2 =1  9 因为x,x 为上式的两根，则 1 2 (1+9k2)x2+18k(1−3k)x+81k2−54k =(1+9k2)(x−x)(x−x ) （1） .................. 9分 1 2 y−1 直线l方程化为x=3+ ． k  y−1 x=3+   k 联立 ，得(1+9k2)y2+(6k−2)y−6k+1=0． ................................ 10分 x2  + y2 =1  9 因为y,y 为上式的两根，则 1 2 (1+9k2)y2+(6k−2)y−6k+1=(1+9k2)(y−y )(y−y )．．（2） ................................ 11分 1 2 y −y y −y (1+9k2)(y −y )(y −y ) 依题意：kk = 0 1 0 2 = 0 1 0 2 1 2 x −x x −x (1+9k2)(x −x)(x −x ) 0 1 0 2 0 1 0 2 (1+9k2)y2+(6k−2)y +1−6k 9y2k2+6(y −1)k+(y −1)2 = 0 0 = 0 0 0 ........ 12分 (1+9k2)x2+18k(1−3k)x +81k2−54k 9(x −3)2k2+18(x −3)k+x2 0 0 0 0 0 下同方法一 19．（17分）帕德近似是法国数学家亨利·帕德发明的用有理多项式近似特定函数的方 法，在计算机数学中有着广泛的应用．已知函数 f(x)在x=0处的[m,n]阶帕德近似定 a +ax+ +a xm 义为：R(x)= 0 1 m ，且满足： 1+bx+ +b xn 1 n f(0)=R(0)， f(0)=R(0)， f(2)(0)=R(2)(0)， ， f(m+n)(0)=R(m+n)(0)． 其中 f(2)(x)=f(x)， f(3)(x)=f(2)(x)  ， ， f(m+n)(x)=f(m+n−1)(x)  ．     1 a+bx+ x2 2 已知 f(x)=ln(x+1)在x=0处的[2,2]阶帕德近似为R(x)= ； 1 1+x+ x2 6 （1）求实数a，b的值； （2）设h(x)= f(x)−R(x)，证明：xh(x)≥0； 1 （3）已知x ，x ，x 是方程lnx=(x− )的三个不等实根，求实数的取值范 1 2 3 x x +x +x 1 围，并证明： 1 2 3  −1． 3  解：（1）依题意可知， f(0)=0，R(0)=a，因为 f(0)=R(0)，所以a=0 ..... 1分 6bx+3x2 1 (18−6b)x2+36x+36b 此时，R(x)= ，因为 f '(x)= ，R(x)= ， 6+6x+x2 1+x (x2+6x+6)2 所以 f(0)=1，R(0)=b 因为 f(0)=R(0)，所以b=1； ............................................................................... 3分 {#{QQABCYQAgggAQJIAARgCQQFQCgMQkBGAACoOwBAMMAIACQNABCA=}#}3x2+6x （2）依题意，h(x)= f(x)−R(x)=ln(1+x)− x2+6x+6 1 12(x2+3x+3) x4 h'(x)= − = ≥0 ........................................ 5分 1+x (x2+6x+6)2 (1+x)(x2+6x+6)2 故h(x)在(−1,+)单调递增， ................................................................................... 6分 由h(0)=0，故x(−1,0)，h(x)0，x(0,+)，h(x)0 综上，x−1，xh(x)≥0； .................................................................................... 7分 1 （3）不妨设x x x ，令t(x)=lnx−(x− )， 1 2 3 x 1 1 −x2+x− t'(x)= −(1+ )= (x0) x x2 x2 当≤0时，t'(x)0，此时t(x)单调递增，t(x)=0不存在三个不等实根； .... 8分 当0时，令s(x)=−x2+x−，其判别式=1−42 1 若=1−42≤0，即≥ ，s(x)≤0恒成立，即t'(x)≤0， 2 此时t(x)单调递减，t(x)=0不存在三个不等实根； ............................................ 9分 1 若=1−42 0，即0 ，t'(x)=0存在两个不等正实根r,r (r r )，此时有 2 1 2 1 2 当x(0,r)时，t'(x)0，t(x)单调递减； 1 当x(r,r )时，t'(x)0，t(x)单调递增； 1 2 当x(r,+)时，t'(x)0，t(x)单调递减； ...................................................... 10分 2 又因为t(1)=0，且t'(1)=1−20，故t(r)0，t(r )0 1 2 1 1 2 因为lnxx−1(x1)，所以ln  −1，即lnx2− x x x 1 2 1 1 1 所以t(4)=ln4−(4− )2− −5+ =(2−5)+ ( −2)0 4 2 3 2  所以存在x (4,r)，满足t(x)=0； ................................................................... 11分 1 1 1 1 1 1 1 又因为t( )=ln −( −x)=−lnx+(x− )=−t(x) x x x x 1 故存在x = ，满足t(x )=0； 3 x 3 1 1 1 故当且仅当0 时，lnx=(x− )存在三个不等实根， ........................... 13分 2 x 1 且满足x x =1x ，且x = 1 2 3 1 x 3 3x2+6x 由（2）可知，当x0时，ln(1+x) x2+6x+6 3x2−3 因此，lnx (x1)................................................................................ 15分 x2+4x+1 1 3x2−3 故lnx =(x − ) 3 ，化简可得： 3 3 x x2+4x +1 3 3 3 3 x2+4x +1 1  3 3 =x +4+ =x +x +x +3  x 3 x 1 2 3 3 3 x +x +x 1 因此 1 2 3  −1，命题得证． ..................................................................... 17分 3  {#{QQABCYQAgggAQJIAARgCQQFQCgMQkBGAACoOwBAMMAIACQNABCA=}#}