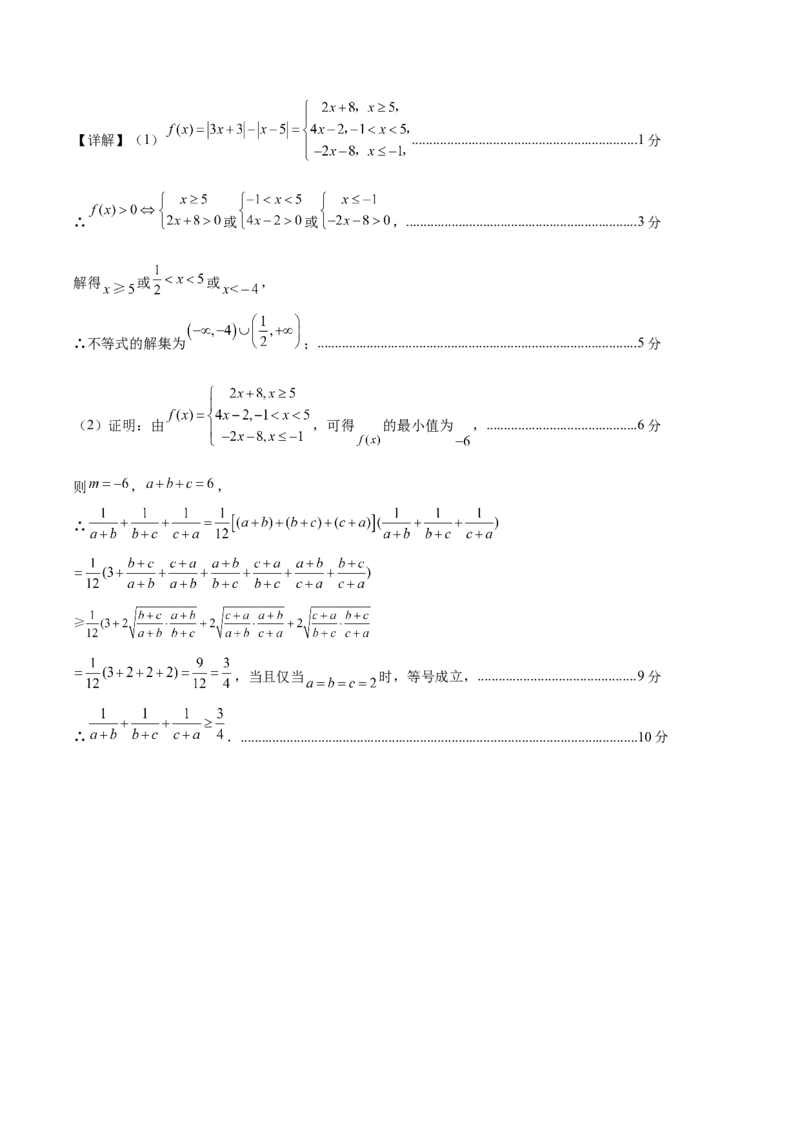文档内容
【赢在高考·黄金8卷】备战2024年高考数学模拟卷(全国卷专用)
黄金卷02(文科)
(考试时间:120分钟 试卷满分:150分)
第 I 卷(选择题)
一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题
目要求的.
1 2 3 4 5 6 7 8 9 10 11 12
D A B C C B D C B C D D
第 II 卷(非选择题)
二、填空题:本大题共4小题,每小题5分,共20分
13.3 14.14 15. 16.
三、解答题:本大题共70分.解答应写出文字说明、证明过程或演算步骤.第17~21题为必考题,每个试
题考生都必须作答.第22、23题为选考题,考生根据要求作答.
(一)必考题:共60分.
17.【答案】(1) , , (2) .
【详解】(1) 中位数为 75 , ,
,.........................................................................................................................................2分
又 ,
,...........................................................................................................................................3分
则平均数为: ..............................................5分
(2)第四组与第五组人数的比为 ,
从第四组抽选4人,记为1,2,3,4,
从第五组抽选2人,记为 ,..........................................................................................................7分
所有基本事件为: ,
共15种,............................................................9分来自同一组的有: ,共7种情况,................................10分
故恰好来自同一组的概率 .........................................................................................................12分
18.【答案】(1) (2)
【详解】(1)由已知 ,根据正弦定理可得 ,................1分
因为 ,所以 ,故有 ,
则有 ,..................................................................................................................3分
因为 ,即 ,可知 ,可得 ,................................................5分
所以 ,则 .....................................................................................................................6分
(2)在 中,根据余弦定理可得 ,
即 ,解得 或 (舍去),.............................................................................8分
由题意可知: ,
由面积关系可得 ,
则 ,.........................................................................10分
即 ,可得 ...........................................................................................................12分
19.【答案】(1)证明见解析(2) .
【详解】(1) ,
, .........................................................................................................1分
平面 平面 ,且交线为 , 平面 ,平面 ,
平面 , .......................................................................................................2分
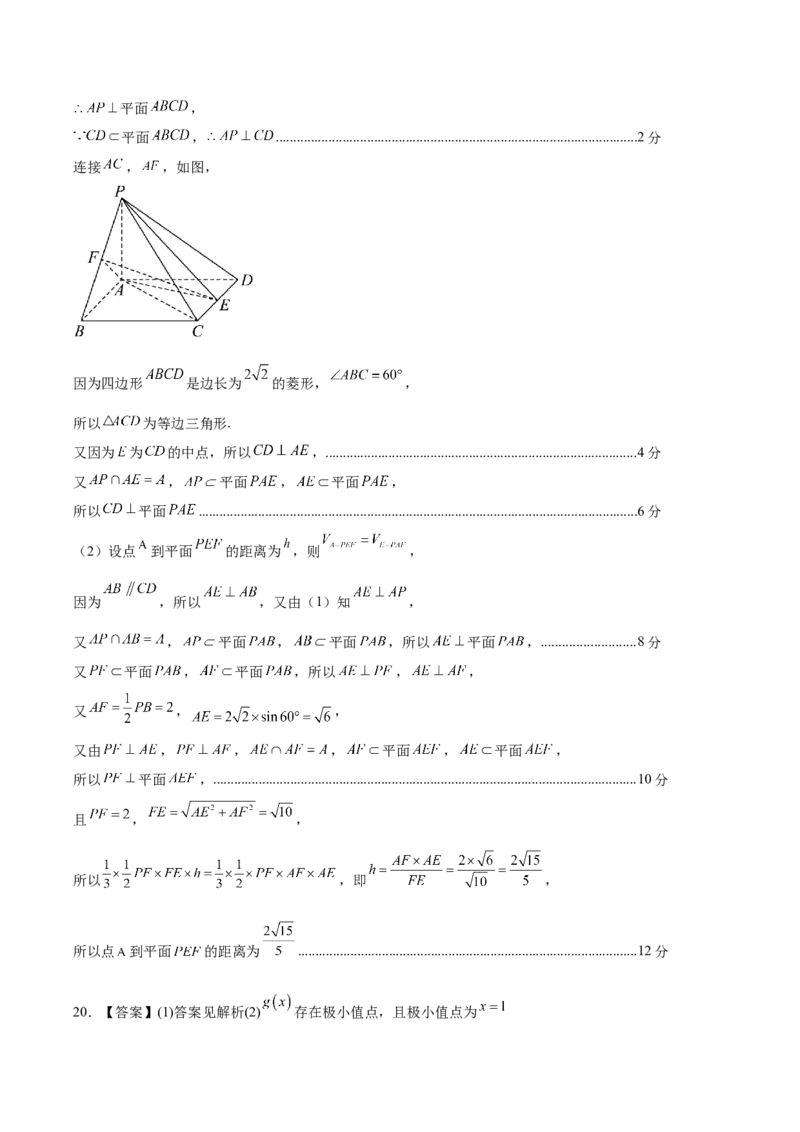
连接 , ,如图,
因为四边形 是边长为 的菱形, ,
所以 为等边三角形.
又因为 为 的中点,所以 ,.........................................................................................4分
又 , 平面 , 平面 ,
所以 平面 .............................................................................................................................6分
(2)设点 到平面 的距离为 ,则 ,
因为 ,所以 ,又由(1)知 ,
又 , 平面 , 平面 ,所以 平面 ,...........................8分
又 平面 , 平面 ,所以 , ,
又 , ,
又由 , , , 平面 , 平面 ,
所以 平面 ,.........................................................................................................................10分
且 , ,
所以 ,即 ,
所以点 到平面 的距离为 .................................................................................................12分
20.【答案】(1)答案见解析(2) 存在极小值点,且极小值点为【详解】(1) , , ,...................................................................1分
当 时, , 在区间 上单调递增;...........................................................2分
当 ,且 时, , 单调递减;
当 时, , 单调递增.................................................................................4分
综上,当 时, 在区间 上单调递增;
当 时, 在区间 上单调递减,在区间 上单调递增..................................5分
(2)当 时, , ,故 .
令 , ,所以 ,........................................................................6分
当 时, , 单调递减;
当 时, , 单调递增...................................................................................8分
又 , , ,
故 ,使得 .
当 时, , , 单调递增;
当 时, , , 单调递减;................................................................10分
当 时, , , 单调递增,
故 存在极小值点,且极小值点为 ......................................................................................12分21.【答案】(1) (2)存在,
【详解】(1)因为 ,所以 .
所以椭圆 的方程为 .......................................................................................................2分
因为点 在椭圆 上,所以 ,解得 ,
所以 ............................................................................................................................................4分
所以椭圆 的标准方程为 .................................................................................................5分
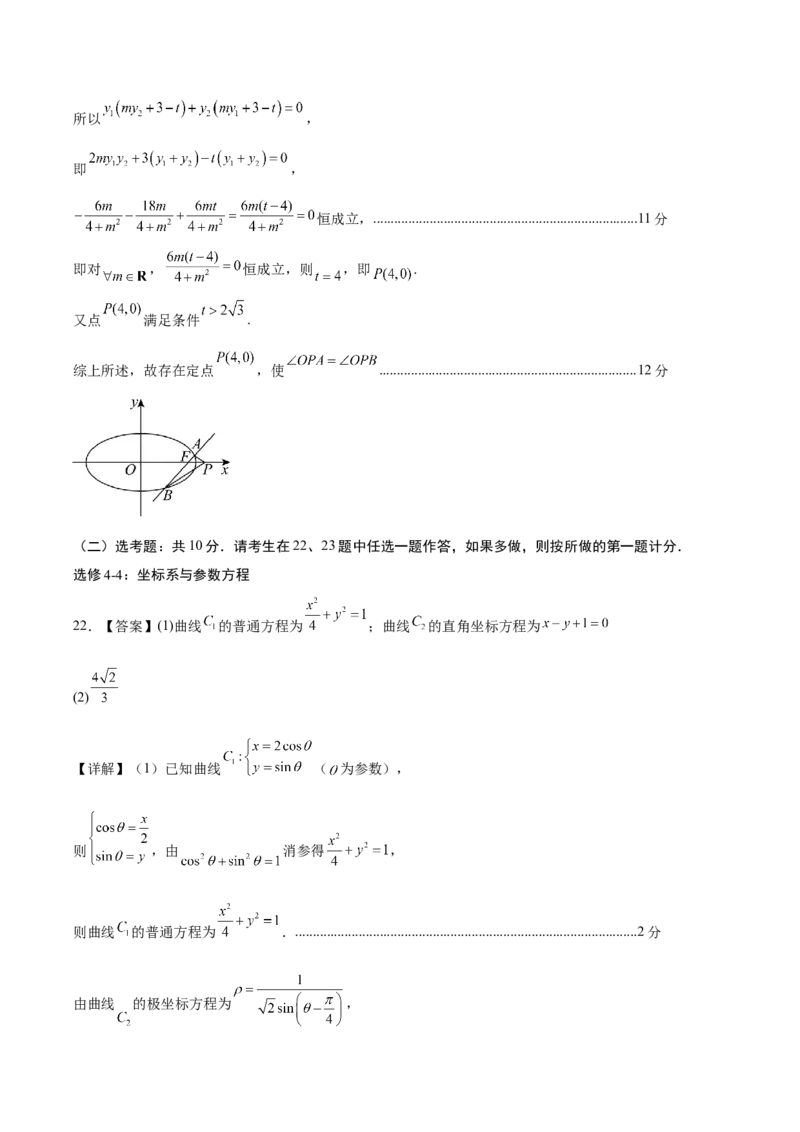
(2)存在定点 ,使 .理由如下:
由(1)知, ,则点 .
设在 轴上存在定点 ,使 成立......................................................................6分
当直线 斜率为 时,直线右焦点 的直线 即 轴与 交于长轴两端点,
若 ,则 ,或 .....................................................................................7分
当直线 斜率不为 时,设直线 的方程为 ,.
由 消去 并整理,得 ,
则 ....................................................................................................9分
因为 ,所以 ,
所以 ,即 .所以 ,
即 ,
恒成立,...........................................................................11分
即对 , 恒成立,则 ,即 .
又点 满足条件 .
综上所述,故存在定点 ,使 .........................................................................12分
(二)选考题:共10分.请考生在22、23题中任选一题作答,如果多做,则按所做的第一题计分.
选修4-4:坐标系与参数方程
22.【答案】(1)曲线 的普通方程为 ;曲线 的直角坐标方程为
(2)
【详解】(1)已知曲线 ( 为参数),
则 ,由 消参得 ,
则曲线 的普通方程为 ..................................................................................................2分
由曲线 的极坐标方程为 ,变形得 ,............................................................................................3分
即 ,且满足 ,
由互化公式 ,得 ,即 .
故曲线 的直角坐标方程为 ........................................................................................5分
(2)由于 在直线l上,
可设直线l的参数方程的标准形式为 (t为参数),
代入曲线 ,
化简得 , ,............................................................................................7分
设A,B对应的参数分别为 , ,
则 , ,................................................................................................................8分
由于 ,故 ,
所以 .
故 的值为 .....................................................................................................................10分
选修4-5:不等式选讲
23.【答案】(1)
(2)证明见解析【详解】(1) ................................................................1分
∴ 或 或 ,..................................................................3分
解得 或 或 ,
∴不等式的解集为 ;...........................................................................................5分
(2)证明:由 ,可得 的最小值为 ,...........................................6分
则 , ,
∴
,当且仅当 时,等号成立,.............................................9分
∴ ..................................................................................................................10分