文档内容
【赢在高考·黄金8卷】备战2024年高考数学模拟卷(全国卷专用)
黄金卷02(文科)
(考试时间:120分钟 试卷满分:150分)
第 I 卷(选择题)
一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题
目要求的.
1.设集合 , ,则 ( )
A. B. C. D.
2.设复数 ,其共扼复数为 ,则 ( )
A. B. C.2 D.
3.已知 , 是两条不同直线, 是平面,且 , ,“ ”是“ ”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
4.( 2023·四川泸州·统考一模)若 , ,则 ( )
A. B. C. D.
5.已知正方形 的边长为 , 在边 上,则 的最大值为( )
A.1 B. C.2 D.
6.我国数学家陈景润在哥德巴赫猜想的研究中取得了世界领先的成果.哥德巴赫猜想是“每个大于2的偶
数可以表示为两个素数的和”,如 .在不超过30的素数中,随机选取两个不同的数,其和等于30的概率是( )
A. B. C. D.
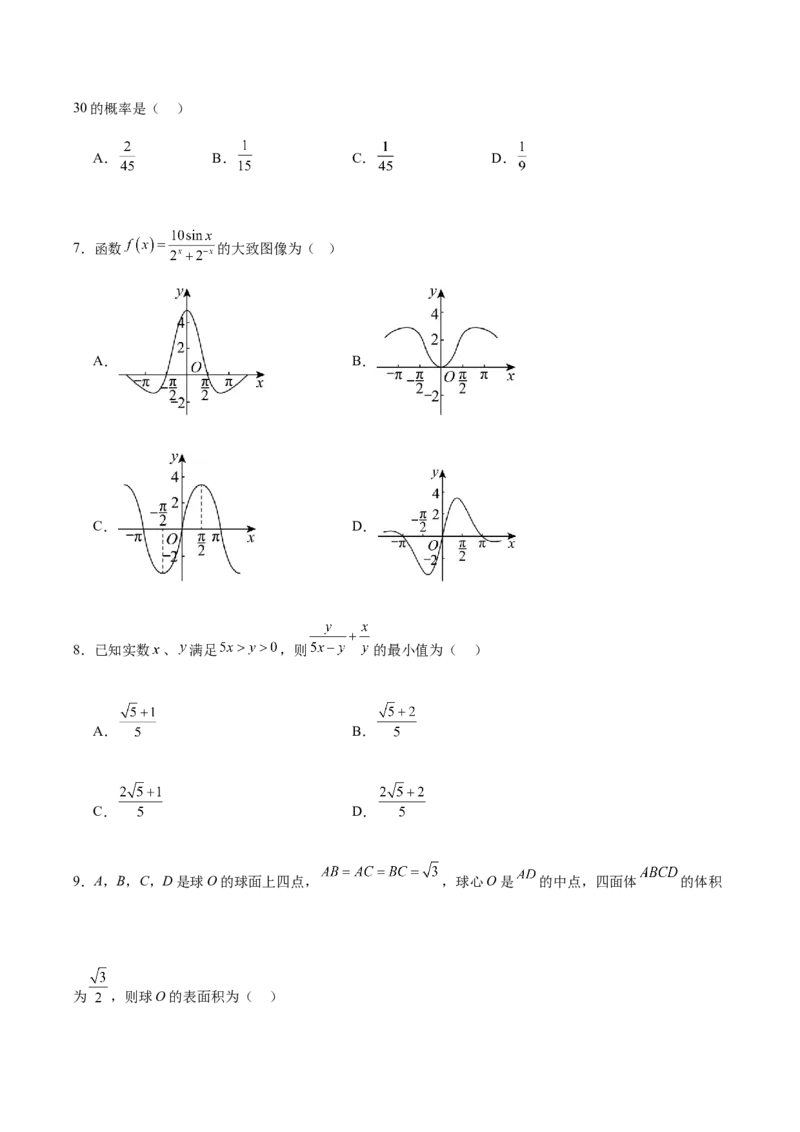
7.函数 的大致图像为( )
A. B.
C. D.
8.已知实数 、 满足 ,则 的最小值为( )
A. B.
C. D.
9.A,B,C,D是球O的球面上四点, ,球心O是 的中点,四面体 的体积
为 ,则球O的表面积为( )A. B. C. D.
10.已知 分别为双曲线 的左、右焦点,过 与双曲线的一条渐近线平行的直线
交双曲线于点 ,若 ,则双曲线的离心率为( )
A.3 B. C. D.2
11.设首项为 的数列 的前n项和为 , ,且 ,则数列 的前23项
和为( )
A. B. C. D.
12.若曲线 存在与直线 垂直的切线,则k的取值范围是( )
A. B.
C. D.
第 II 卷(非选择题)
二、填空题:本大题共4小题,每小题5分,共20分
13.已知 中, ,且 ,则 的面积是 .14.若实数 满足约束条件 ,则 的最大值为 .
15.若直线l: 与圆C: 相交于A,B两点, ,则直线l的斜率的
取值范围为 .
16.已知 为偶函数,且当 时, ,其中 为 的导数,则不等式
的解集为 .
三、解答题:本大题共70分.解答应写出文字说明、证明过程或演算步骤.第17~21题为必考题,每个试
题考生都必须作答.第22、23题为选考题,考生根据要求作答.
(一)必考题:共60分.
17.(12分)某校为了宣传垃圾分类知识,面向该校学生开展了“垃圾分类知识”网络问卷调查,每位学
生仅有一次参与机会,通过抽样,得到 100 人的得分情况,将样本数据分成
五组,并整理得到如下频率分布直方图;已知成绩的中位数为 75
(1)求 的值,并求出成绩的平均数(同一组中的每个数据可用该组区间中点值代替);
(2)现用分层抽样从第四组和第五组按照比例抽选出 6 人进行垃圾分类知识竞答活动,再从中选出两人进
行一对一 ,求抽出的两人恰好来自同一组的概率.18.(12分)记 的内角A, , 所对的边分别是 , , ,已知 .
(1)求角 的大小;
(2)若点 在边 上, 平分 , , ,求线段 长.
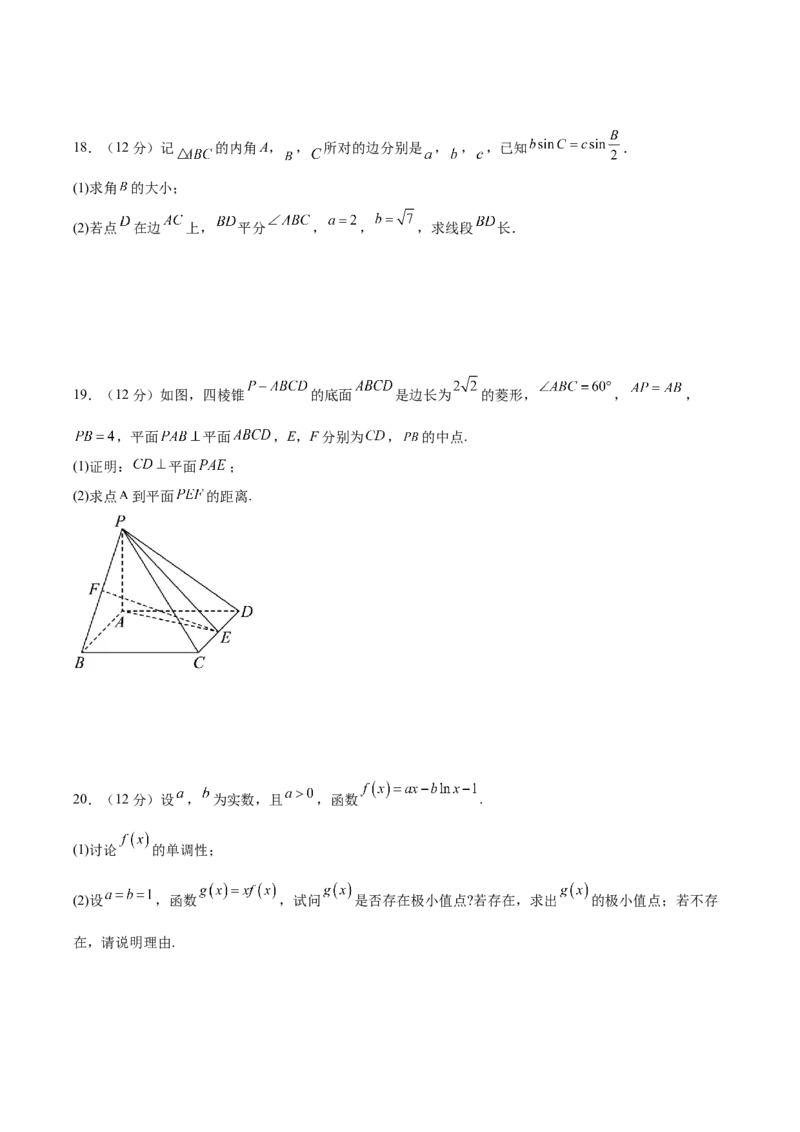
19.(12分)如图,四棱锥 的底面 是边长为 的菱形, , ,
,平面 平面 ,E,F分别为 , 的中点.
(1)证明: 平面 ;
(2)求点 到平面 的距离.
20.(12分)设 , 为实数,且 ,函数 .
(1)讨论 的单调性;
(2)设 ,函数 ,试问 是否存在极小值点?若存在,求出 的极小值点;若不存
在,请说明理由.21.(12分)已知椭圆 的离心率为 ,且过点 .
(1)求椭圆 的标准方程.
(2)已知过右焦点 的直线 与 交于 两点,在 轴上是否存在一个定点 ,使 ?若存在,
求出定点 的坐标;若不存在,请说明理由.
(二)选考题:共10分.请考生在22、23题中任选一题作答,如果多做,则按所做的第一题计分.
选修4-4:坐标系与参数方程
22.(10分)平面直角坐标系 中,曲线 的参数方程为 ( 为参数).以原点O为极点,x
轴的正半轴为极轴建立极坐标系,曲线 的极坐标方程为 .
(1)求曲线 的普通方程和曲线 的直角坐标方程;
(2)已知点 ,记 和 交于 两点,求 的值.
选修4-5:不等式选讲
23.(10分)已知函数 .
(1)求不等式 的解集 ;(2)若 是 的最小值,且正数 满足 ,证明: .