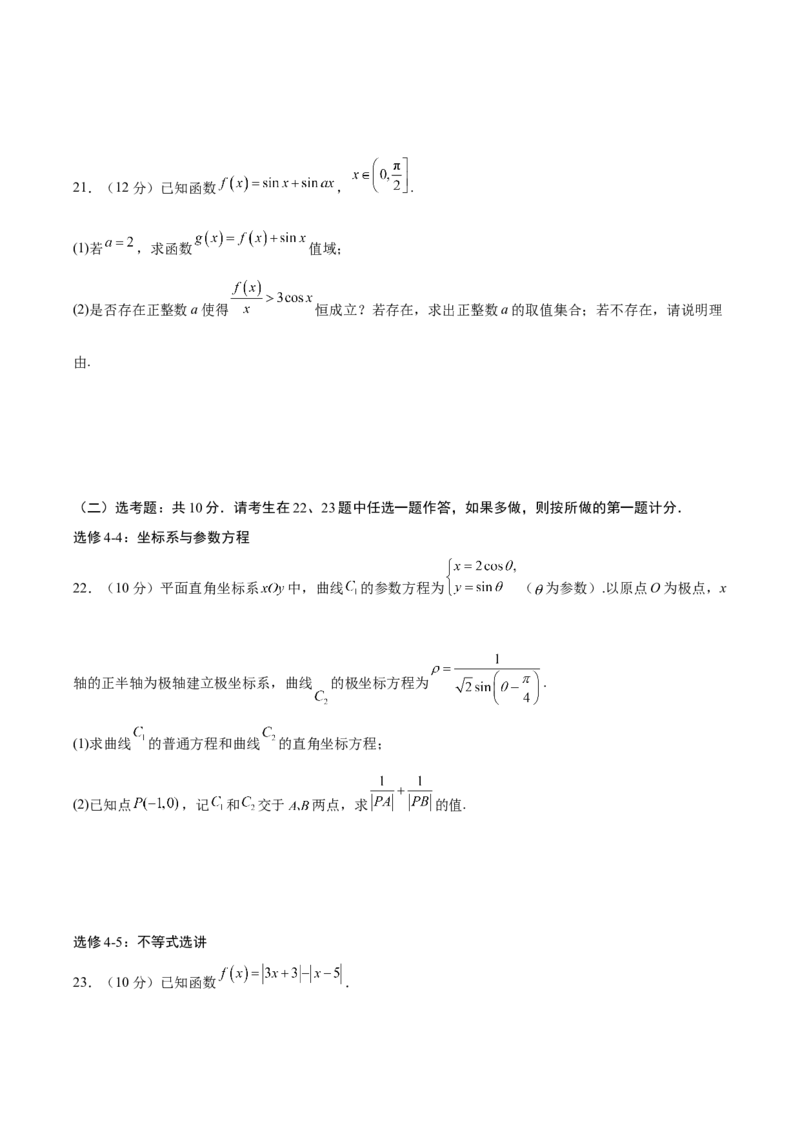文档内容
【赢在高考·黄金8卷】备战2024年高考数学模拟卷(全国卷专用)
黄金卷02
(考试时间:120分钟 试卷满分:150分)
第 I 卷(选择题)
一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题
目要求的.
1.设集合 ,则 ( )
A. B. C. D.
2.设复数 满足 ,则 ( )
A. B. C. D.
3.命题 :函数 的最大值为 ,函数 的最小值为 ;命题 : 的最大
值为 ,则 是 的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分又不必要条件
4.函数 的图像大致为( )
A. B.
C. D.
5.已知向量 ,且 ,则实数 构成的集合是( )
A. B.C. D.
6.若两个正实数 满足 ,且不等式 有解,则实数 的取值范围是( )
A. B. C. D.
7.为落实立德树人的根本任务,践行五育并举,某学校开设 三门劳动教育校本课程,现有甲、乙、
丙、丁、戊五位同学报名参加该校劳动教育校本课程的学习,每位同学仅报一门,每门至少有一位同学参
加,则不同的报名方法有( )
A.60种 B.150种 C.180种 D.300种
8.已知 其中 则 ( )
A. B. C. D.
9.已知三棱锥 的四个顶点在球 的球面上,点 分别是 的中点, ,
,则( )
A.三棱锥 的体积为16 B.三棱锥 的表面积为
C.球 的表面积为 D.球 的体积为
10.已知双曲线 : ( , )的右焦点为 , 、 两点在双曲线的左、右两支上,
且 , , ,且点 在双曲线上,则双曲线的离心率为( )
A. B. C. D.
11.已知定义在 上的函数 满足 , 为 的导函数,当时, ,则不等式 的解集为( )
A. B.
C. D.
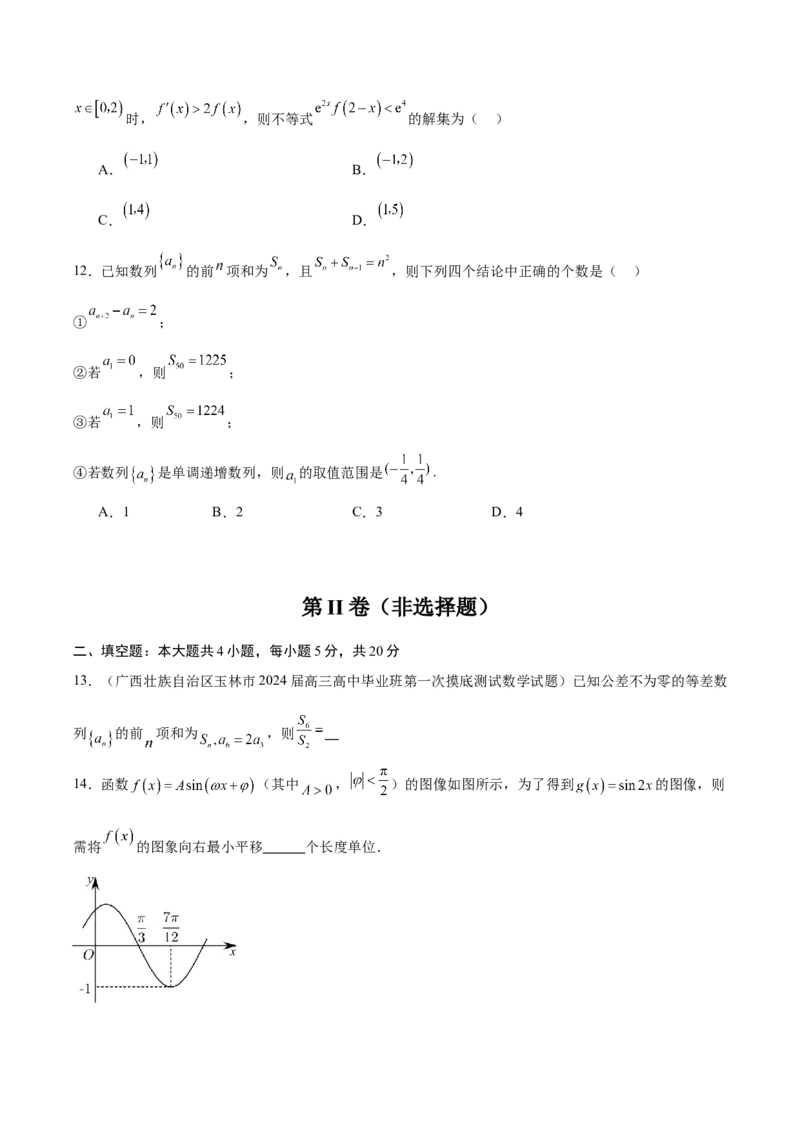
12.已知数列 的前 项和为 ,且 ,则下列四个结论中正确的个数是( )
① ;
②若 ,则 ;
③若 ,则 ;
④若数列 是单调递增数列,则 的取值范围是 .
A.1 B.2 C.3 D.4
第 II 卷(非选择题)
二、填空题:本大题共4小题,每小题5分,共20分
13.(广西壮族自治区玉林市2024届高三高中毕业班第一次摸底测试数学试题)已知公差不为零的等差数
列 的前 项和为 ,则
14.函数 (其中 , )的图像如图所示,为了得到 的图像,则
需将 的图象向右最小平移 个长度单位.15.米斗是称量粮食的量器,是古代官仓、粮栈、米行的必备的用具.为使坚固耐用,米斗多用上好的木
料制成.米斗有着吉祥的寓意,是丰饶富足的象征,带有浓郁的民间文化韵味,如今也成为了一种颇具意
趣的藏品.如图的米斗可以看作一个正四棱台,已知该米斗的侧棱长为10,两个底边长分别为8和6,则
该米斗的外接球的表面积是 .
16.已知关于 的方程 在 上有两个不相等的实根,则实数 的取值范围是
三、解答题:本大题共70分.解答应写出文字说明、证明过程或演算步骤.第17~21题为必考题,每个试
题考生都必须作答.第22、23题为选考题,考生根据要求作答.
(一)必考题:共60分.
17.(12分)目前,教师职业越来越受青睐,考取教师资格证成为不少人的就业规划之一.当前,中小学教师资
格考试分笔试和面试两部分,笔试通过后才能进入面试环节.已知某市 年共有 名考生参加了中小
学教师资格考试的笔试,笔试成绩 ,只有笔试成绩高于 分的学生才能进入面试环节.
(1)从报考中小学教师资格考试的考生中随机抽取 人,求这 人中至少有一人进入面试的概率;
(2)现有甲、乙、丙 名学生进入了面试,且他们通过面试的概率分别为 ,设这 名学生中通过面试的
人数为 ,求随机变量 的分布列和数学期望.
参考数据:若 ,则 , ,
, , .
18.(12分)在 中,角 , , 所对的边分别为 , , .已知 .(1)求角 的大小;
(2)设 ,求 的取值范围.
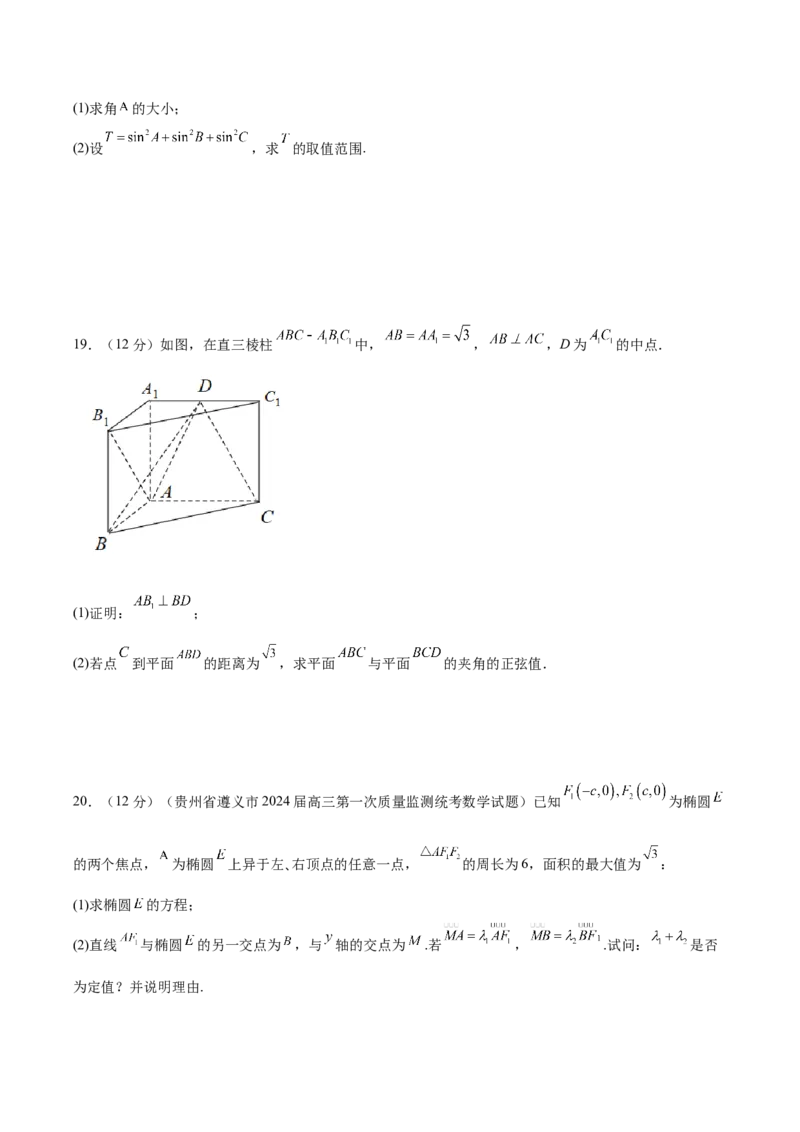
19.(12分)如图,在直三棱柱 中, , ,D为 的中点.
(1)证明: ;
(2)若点 到平面 的距离为 ,求平面 与平面 的夹角的正弦值.
20.(12分)(贵州省遵义市2024届高三第一次质量监测统考数学试题)已知 为椭圆
的两个焦点, 为椭圆 上异于左、右顶点的任意一点, 的周长为6,面积的最大值为 :
(1)求椭圆 的方程;
(2)直线 与椭圆 的另一交点为 ,与 轴的交点为 .若 , .试问: 是否
为定值?并说明理由.21.(12分)已知函数 , .
(1)若 ,求函数 值域;
(2)是否存在正整数a使得 恒成立?若存在,求出正整数a的取值集合;若不存在,请说明理
由.
(二)选考题:共10分.请考生在22、23题中任选一题作答,如果多做,则按所做的第一题计分.
选修4-4:坐标系与参数方程
22.(10分)平面直角坐标系 中,曲线 的参数方程为 ( 为参数).以原点O为极点,x
轴的正半轴为极轴建立极坐标系,曲线 的极坐标方程为 .
(1)求曲线 的普通方程和曲线 的直角坐标方程;
(2)已知点 ,记 和 交于 两点,求 的值.
选修4-5:不等式选讲
23.(10分)已知函数 .(1)求不等式 的解集 ;
(2)若 是 的最小值,且正数 满足 ,证明: .