文档内容
【赢在高考·黄金8卷】备战2024年高考数学模拟卷(全国卷专用)
黄金卷03
(考试时间:120分钟 试卷满分:150分)
第 I 卷(选择题)
一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题
目要求的.
1.设集合 ,集合 , ,则 ( )
A. B. C. D.
【答案】B
【分析】先求得集合 ,结合集合的运算法则,逐项判定,即可求解.
【详解】由集合 , ,
可得 或 , ,
对于A中,可得 ,不符合题意;
对于B中,可得 ,符合题意;
对于C中,可得 ,不符合题意;
对于D中,可得 ,不符合题意.
故选:B.
2.已知 为虚数单位,且 ,则 ( )
A.3 B. C.5 D.
【答案】C
【分析】依题意先对原式进行化简,可求得 ,利用共轭复数的定义可得 ,再利用复数的运算可求得答
案.【详解】由题意得: ,则 ,
.
故选:C.
3.已知 , , 为三条不同的直线, , 为两个不同的平面,则下列命题错误的是( )
A.若 , , ,则 B.若 , , , ,则
C.若 , , ,则 D.若 , , ,则
【答案】B
【分析】根据线面平行的判定定理可判断A;根据线面垂直的判定定理可判断B;根据线面平行的性质定
理可判断C;根据面面平行以及线面垂直的性质可判断D.
【详解】对于A, ,则 内必存在直线,设为s,使得 ,
又 ,则 ,而 ,则 ,A正确;
B中,若 ,此时有可能是 或 或 或m和 相交不垂直,
未必一定是 ,则B的说法不正确.
对于C,若 , , ,则 ,
根据线面平行的性质定理可知 ,C正确,
对于D,若 , ,则 ,又 ,故 ,D正确,
故选:B.
4.函数 的大致图象是( )
A. B.
C. D.
【答案】A
【分析】根据函数为奇函数排除BD,再根据函数值的符号排除选项C.【详解】易知函数 的定义域为R,且 ,
所以函数 为奇函数,其图象关于原点对称,故选项BD不符合.
当 时,函数值为 ,故选项C不符合,选项A符合.
故选:A.
5.已知向量 ,若 ,则 ( )
A. B. C. D.
【答案】A
【分析】根据两个向量垂直则数量积为0运算即可.
【详解】 ,
又 ,所以 ,
即 ,解得 ,所以 ,所以 ,
故选:A
6.已知函数 ,若对任意的正数 、 ,满足 ,则 的最小值为( )
A. B. C. D.
【答案】B
【分析】分析函数 的单调性和奇偶性,可得出 ,将代数式 与 相乘,展开后
利用基本不等式可求得 的最小值.
【详解】对任意的 , ,所以,函数 的定义域为 ,
因为 ,即函数 为奇函数,又因为 ,且函数 在 上为增函数,
所以,函数 在 上为增函数,
对任意的正数 、 ,满足 ,则 ,
所以, ,即 ,
所以, ,
当且仅当 时,即当 时,等号成立,故 的最小值为 .
故选:B.
7.2022年10月16日至10月22日,中国共产党第二十次全国人民代表大会在北京召开.会议圆满结束后,
某市为了宣传好二十大会议精神,市宣传部决定组织 去甲、乙、丙、丁4个村开展二十大宣讲
工作,每村至少1人,其中 不去甲村,且 不去同一个村,则宣讲的分配方案种数为( )
A.216 B.198 C.180 D.162
【答案】D
【分析】分 单独去一个村和 与除 以外的另外一人去一个村两种情况讨论,即可得解.
【详解】当 单独去一个村时,有 种,
当 与除 以外的另外一人去一个村时,有 种,
所以共有 种分配方案.
故选:D
8.若 ,则 ( )
A. B. C. D.【答案】A
【分析】利用余弦的二倍角公式和诱导公式结合已知求解即可.
【详解】因为 ,
所以
.
故选:A.
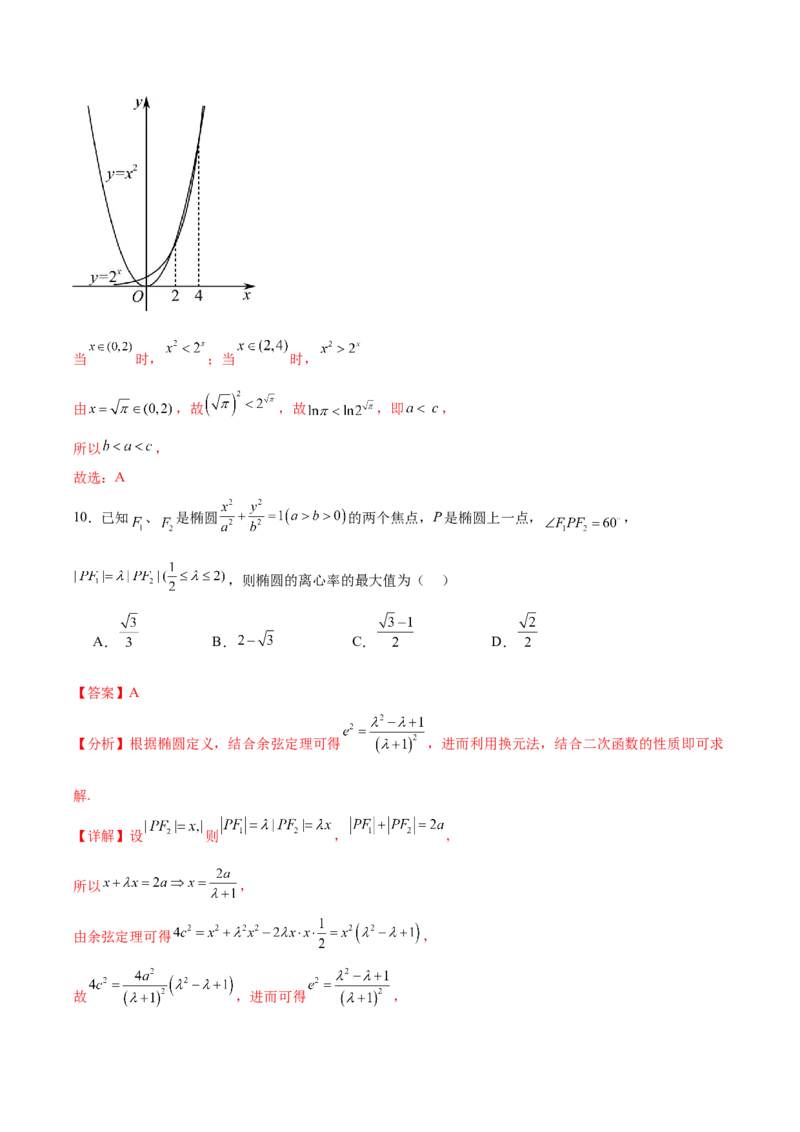
9.已知 ,则 的大小关系是( )
A. B. C. D.
【答案】A
【分析】利用对数函数和指数函数,幂函数的性质求解.
【详解】 , ,即 ,
,
下面比较 与 的大小,构造函数 与 ,
由指数函数 与幂函数 的图像与单调性可知,当 时, ;当 时,
由 ,故 ,故 ,即 ,
所以 ,
故选:A
10.已知 、 是椭圆 的两个焦点,P是椭圆上一点, ,
,则椭圆的离心率的最大值为( )
A. B. C. D.
【答案】A
【分析】根据椭圆定义,结合余弦定理可得 ,进而利用换元法,结合二次函数的性质即可求
解.
【详解】设 则 , ,
所以 ,
由余弦定理可得 ,
故 ,进而可得 ,令 ,则 , ,
令 ,所以 ,对称轴为 ,
所以 在 单调递减,在 单调递增,
故当 和 时, ,
故 的最大值为 ,
所以 ,故 的最大值为 ,
故选:A
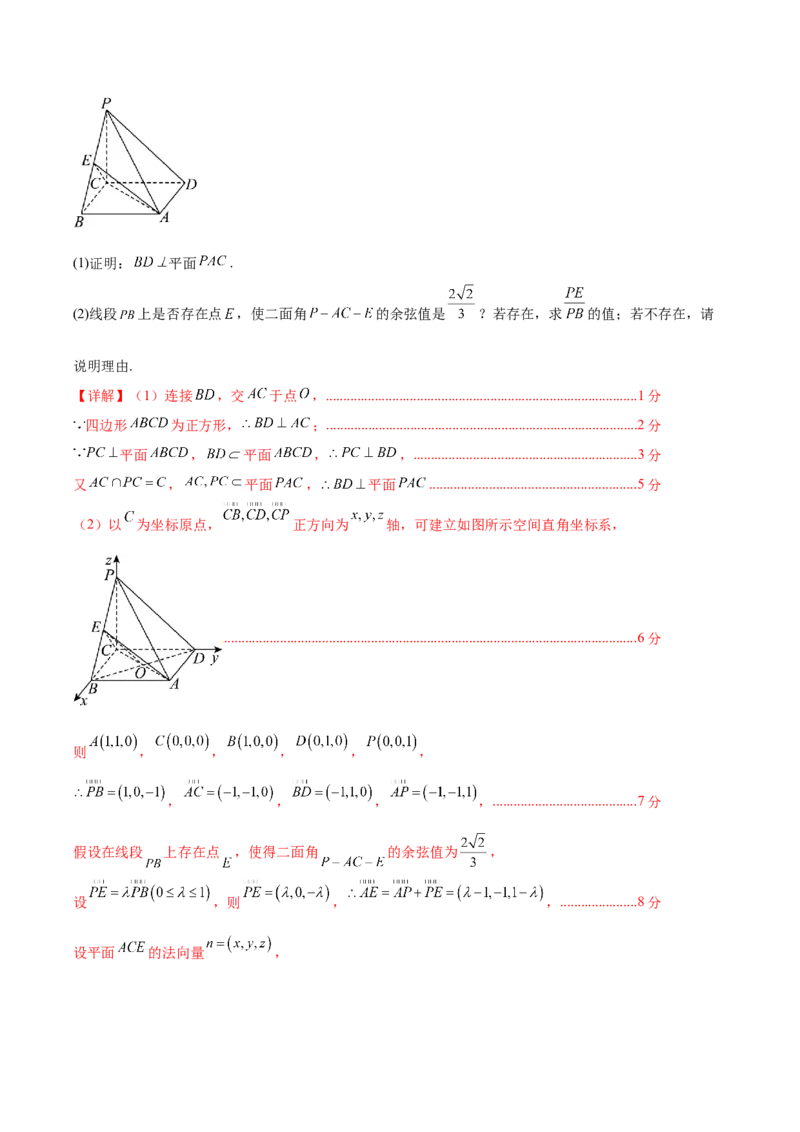
11.如图,正方体 的棱长为3,点P是平面 内的动点,M,N分别为 , 的中
点,若直线BP与MN所成的角为 ,且 ,则动点P的轨迹所围成的图形的面积为( )
A. B. C. D.【答案】A
【分析】连接 , ,得到 ,把BP与MN所成的角就是直线BP与 所成的角,在正方体
中,证得 平面 ,得到 ,设 与平面 的交点为G,连接PG,
结合题意,得到点P的轨迹是以G为圆心, 为半径的圆,根据圆的面积公式,即可求解.
【详解】如图所示,连接 , ,则N为 的中点,又M为 的中点,所以 ,
因此直线BP与MN所成的角就是直线BP与 所成的角,
在正方体 中,可得 ,
因为 平面 , 平面 ,可得 ,
又因为 且 平面 ,所以 平面 ,
因为 平面 ,所以 ,同理可得 ,
因为 ,且 平面 ,所以 平面 ,则 .
设 与平面 的交点为G,连接PG,所以 ,
在直角 中, ,因为 ,所以 ,
又由 ,所以 ,
所以点P的轨迹是以G为圆心, 为半径的圆,其面积为 .
故选:A.12.已知函数 有两个极值点 , ( ),函数 有两个极
值点 , ( ),设 ,则( )
A. B.
C. D.
【答案】C
【分析】解法一:求出函数的导函数,则 , 是方程 的两个实数根, , 是方程 ,
即 的两个实数根,设 ,利用导数求出函数的单调区间,即可得到 ,
, ,从而得到 ,最后根据对勾函数的性质计算可得;
解法二:求导可得 , 是 与 图象交点的横坐标; , 是 与 图象的交点
的横坐标,结合反函数的性质得到 , ,从而求出 的取值范围.
【详解】解法一:由 可得 ,则 , 是方程 的两个实数根,
由 可得 ,则 , 是方程 ,
即 的两个实数根.设 ,则 ,
当 时 ,当 时 ,
故 在 上单调递减,在 上单调递增,则 在 处取得极小值 ,
因为 , 是方程 的两个实数根, , 是方程 的两个实数根,
且 , ,所以 , , ,
则 , , ,
所以 ,
又 在 上单调递增,所以 .
解法二 第一步:对函数求导,将问题进行转化;
由 可得 ,则 , 是方程 的两个实数根,即 与 图象
交点的横坐标.
由 可得 ,则 , 是方程 的两个实数,即 与
图象的交点的横坐标.
第二步:构造函数,求得 的取值范围;
由 可得 ,设 ,则 ,
易得 在 处取得极小值,且 ,当 时, ,当 时, ,
所以由方程 有两个实数根可得 ,即 .
(点拨:因为 与 互为反函数,且 与 互为反函数,所以当 与 的图象有两个交点时, 与 的图象也有两个交点)
第三步:利用反函数的概念对变量进行代换,即可得解;
设 , , , ,
由 与 互为反函数,且 与 互为反函数,
可得 与 , 与 分别关于直线 对称,则 , ,
则 ,
又 在 上单调递增,所以 .
故选:C
【点睛】关键点睛:本题数量关系比较多,关键是得到 , 是方程 的两个实数根, , 是方
程 的两个实数根,从而构造函数.
第 II 卷(非选择题)
二、填空题:本大题共4小题,每小题5分,共20分
13.定义“等和数列”:在一个数列中,如果每一项与它后一项的和都为同一个常数,那么这个数列叫做
等和数列,这个常数叫做该数列的公和.已知数列 是等和数列,且 ,公和为1,那么这个数列的
前2023项和 .
【答案】1010
【分析】根据等和数列的性质可以求出奇数项都相等,偶数项也都相等,最后求和即可.
【详解】由等和数列概念可得 ,
所以 ,
故答案为:101014.将函数 图象上所有点的横坐标变为原来的 ,再向左平移 个单位
长度,得到函数 的图象,若对任意的 ,均有 成立,则 的最小值为 .
【答案】
【分析】先由二倍角公式与两角和与差的正弦公式得 ,再结合三角函数的平移变换得
,由 恒成立可知 , 取最大值,则可求 的表达式,结
合 的条件可得答案.
【详解】由题意得 ,
则 ,因为对任意的 ,均有 成立,所以
,即 ,又 ,所以当 时, 的最小值为 ,
故答案为: .
15.已知 是球 的球面上的三点, ,且三棱锥 的体积为 ,
则球 的体积为 .
【答案】
【分析】判断 的形状并求出其外接圆的半径 ,利用锥体的体积公式求出球心到截面 的距离,
进而求出球半径即可求解.
【详解】在 中, ,由余弦定理得 ,即 ,整理得 ,而 ,解得 ,
显然 ,即 ,则 外接圆的半径 ,
令球心 到平面 的距离为 ,而 的面积为 ,
由棱锥 的体积为 ,得 ,解得 ,
球 的半径 ,则有 , ,
所以球 的体积 .
故答案为:
16.已知关于 的不等式 恰有3个不同的正整数解,则实数 的取值范围是 .
【答案】
【分析】由题意知,关于x的不等式 恰有3个不同的正整数解.设函数 ,
,作出函数图象,由图象观察,可得实数的k取值范围.
【详解】当 时,不等式 有无数个正整数解,不满足题意;
当 时,当 时,不等式 恒成立,有无数个不同的正整数解,不满足题意;
当 时,不等式 等价于 ,
令 ,所以 ,当 时, ,函数 单调递减,当 时, ,函数 单调递增,当 时,
,函数 单调递减,
又 ,结合单调性可知,当 时, 恒成立,
而 表示经过点 的直线,
由图像可知,关于 的不等式 恰有3个不同的正整数解,故只需满足以下条件:
解得 .则实数 的取值范围是 ,
故答案为: .
【点睛】用数形结合思想解决不等式解的问题一般有以下几类:
(1)解含参不等式:在解决含有参数不等式时,由于涉及参数,往往需要讨论,导致演算过程复杂,若
利用数形结合的方法,问题将简单化;
(2)确定参数范围:在确定不等式参数的范围时,几何图形更能使问题直观;
(3)证明不等式:把证明的不等式赋予一定的几何意义,将复杂的证明问题明快解决.
三、解答题:本大题共70分.解答应写出文字说明、证明过程或演算步骤.第17~21题为必考题,每个试
题考生都必须作答.第22、23题为选考题,考生根据要求作答.(一)必考题:共60分.
17.(12分)在 中, ,D为 中点.
(1)若 ,求 ;
(2)若 ,求 的值.
【详解】(1)如图所示:
因为 ,所以 ,
所以 ,所以 ,...................1分
在 中,由余弦定理的推论得: ,
在 中,由余弦定理的推论得: ,........................................3分
所以 ,..............................................................................4分
因为 是边 的中点,所以 ,代入上式整理得 ,
因为 ,所以 ,
解得 或 (舍去),所以 ;.................................................................6分
(2)在 中,由正弦定理得: ,
又 , , ,..........................................................................8分
所以 ,即 ,.............................................................................9分
在 中,由正弦定理得: , , ,所以 .................................................................................................12分
18.(12分)为了让观赏游玩更便捷舒适,常州恐龙园推出了代步工具租用服务.已知有脚踏自行车 与
电动自行车 两种车型,采用分段计费的方式租用. 型车每 分钟收费 元(不足 分钟的部分按 分
钟计算), 型车每 分钟收费 元(不足 分钟的部分按 分钟计算),现有甲乙丙丁四人,分别相
互独立地到租车点租车骑行(各租一车一次),设甲乙丙丁不超过 分钟还车的概率分别为 ,
并且四个人每人租车都不会超过 分钟,甲乙丙均租用 型车,丁租用 型车.
(1)求甲乙丙丁四人所付的费用之和为25元的概率;
(2)求甲乙丙三人所付的费用之和等于丁所付的费用的概率;
(3)设甲乙丙丁四人所付费用之和为随机变量 ,求 的概率分布和数学期望.
【详解】(1)记“甲乙丙丁四人所付的费用之和为25元”为事件 ,即4人均不超过30分钟,
则 .
答:求甲乙丙丁四人所付的费用之和为25元的概率是 ...................................................2分
(2)由题意,甲乙丙丁在 分钟以上且不超过 分钟还车的概率分别为 ,
设“甲乙丙三人所付费用之和等于丁所付费用”为事件 ,
则
答:甲乙丙三人所付的费用之和等于丁所付的费用的概率是 . ...................................5分
(3)①若“4人均不超过30分钟”此时随机变量 的值为25,即为事件 ,由(1)所以 .6分
②记“4人中仅有一人超过30分钟”为事件 ,事件 又分成两种情况“超过30分钟的这一人是甲乙丙
中的一个”和“超过30分钟的这一人是丁”,分别将上述两种情况记为
事件 和 .
i.事件 对应的 的值为30,此时 ;
ii.事件 对应的 的值为35,此时 ............................................................7分③记“4人中仅有两人超过30分钟”为事件 ,事件 又分成两种情况“超过30分钟的两人是甲乙丙中
的两个”和“超过30分钟的两人是甲乙丙中的一个和丁”,分别将上述两种情况记为事件 和 .
i.事件 对应的 的值为35,此时 ;
i.事件 对应的 的值为40,此时 ..................8分
④记“4人中仅有三人超过30分钟”为事件 ,事件 又分成两种情况“超过30分钟的三人是甲乙丙”
和“超过30分钟的三人是甲乙丙中的两个和丁”,分别将上述两种情况记为事件 和 .
i.事件 对应的 的值为40,此时 ;
i.事件 对应的 的值为45,此时 .................9分
⑤记“4人均超过30分钟”为事件 ,则随机变量 的值为50,
此时 ;....................................................10分
所以甲乙丙丁四人所付费用之和的分别为
25 30 35 40 45 50
.................................................................................................................................................................11分
所以 .
答:甲乙丙丁四人所付费用之和 的数学期望为 ...................................................................12分
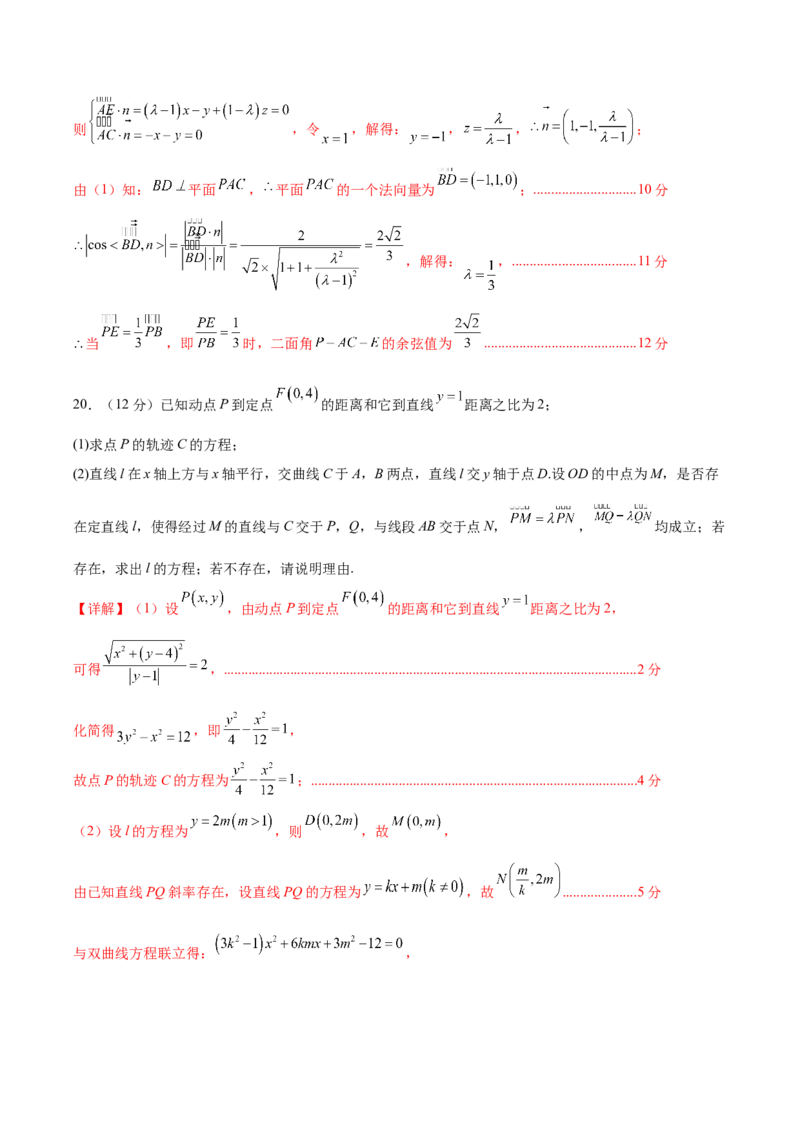
19.(12分)如图,在四棱锥 中,已知底面 是正方形, 底面 ,且
, 是棱 上动点.(1)证明: 平面 .
(2)线段 上是否存在点 ,使二面角 的余弦值是 ?若存在,求 的值;若不存在,请
说明理由.
【详解】(1)连接 ,交 于点 ,.........................................................................................1分
四边形 为正方形, ;.........................................................................................2分
平面 , 平面 , ,................................................................3分
又 , 平面 , 平面 ...........................................................5分
(2)以 为坐标原点, 正方向为 轴,可建立如图所示空间直角坐标系,
......................................................................................................................6分
则 , , , , ,
, , , ,.........................................7分
假设在线段 上存在点 ,使得二面角 的余弦值为 ,
设 ,则 , ,......................8分
设平面 的法向量 ,则 ,令 ,解得: , , ;
由(1)知: 平面 , 平面 的一个法向量为 ;.............................10分
,解得: ,...................................11分
当 ,即 时,二面角 的余弦值为 ...........................................12分
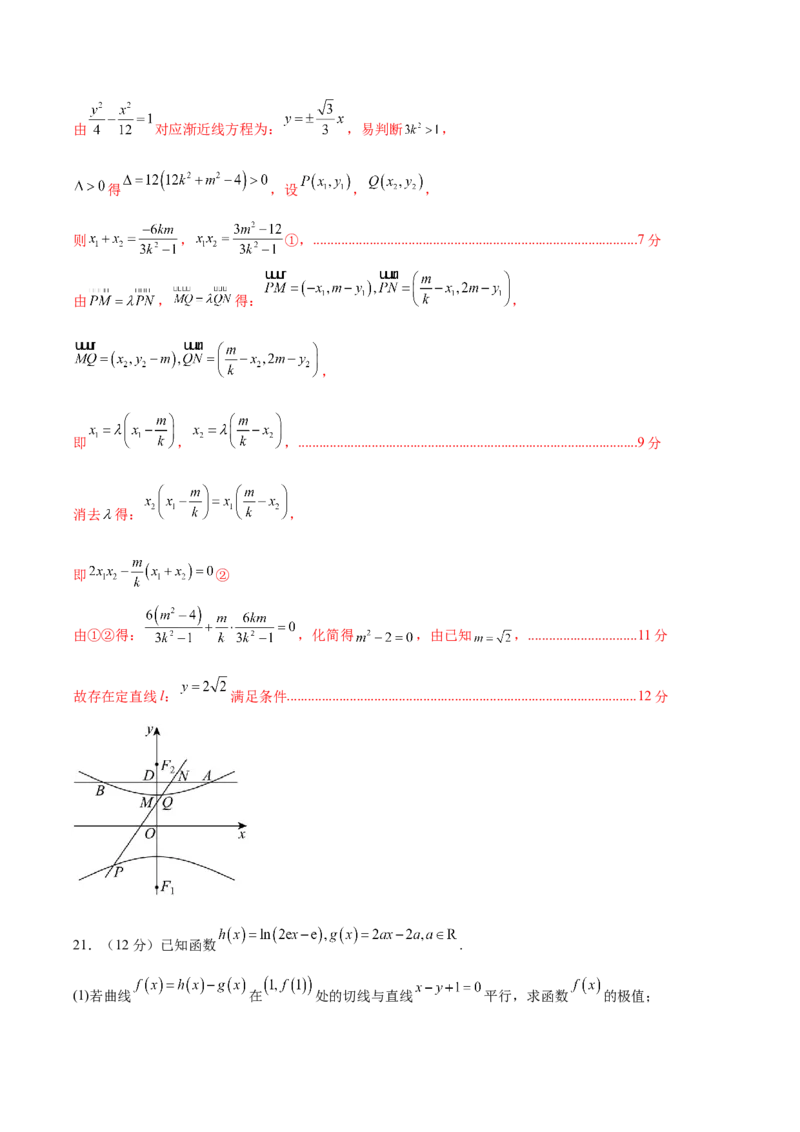
20.(12分)已知动点P到定点 的距离和它到直线 距离之比为2;
(1)求点P的轨迹C的方程;
(2)直线l在x轴上方与x轴平行,交曲线C于A,B两点,直线l交y轴于点D.设OD的中点为M,是否存
在定直线l,使得经过M的直线与C交于P,Q,与线段AB交于点N, , 均成立;若
存在,求出l的方程;若不存在,请说明理由.
【详解】(1)设 ,由动点P到定点 的距离和它到直线 距离之比为2,
可得 ,......................................................................................................................2分
化简得 ,即 ,
故点P的轨迹C的方程为 ;.............................................................................................4分
(2)设l的方程为 ,则 ,故 ,
由已知直线PQ斜率存在,设直线PQ的方程为 ,故 .....................5分
与双曲线方程联立得: ,由 对应渐近线方程为: ,易判断 ,
得 ,设 , ,
则 , ①,............................................................................................7分
由 , 得: ,
,
即 , ,.................................................................................................9分
消去 得: ,
即 ②
由①②得: ,化简得 ,由已知 ,...............................11分
故存在定直线l: 满足条件....................................................................................................12分
21.(12分)已知函数 .
(1)若曲线 在 处的切线与直线 平行,求函数 的极值;(2)已知 ,若 恒成立.求证:对任意正整数 ,都有 .
【详解】(1)由 ,可得 ,.................................1分
由条件可得 ,即 .............................................................................................2分
则 ,
令 可得 ,当 时, ,当 时, .
在 上单调递减,在 上单调递增,................................................................4分
的极大值为 ,无极小值...........................................................5分
(2) ,即 对任意的 恒成立,
即 ,其中 ,...............................................................................................6分
令 ,则 ,即 ,........................................................................7分
构造函数 ,则 ,令 ,得 ,列表如下:
+ 0 -
极大值
所以,函数 的单调递增区间为 ,单调递减区间为 ,
所以, ,....................................................................................................9分
即 时, 恒成立,取 ,则 对任意的 恒成立,............................................................10分
令 ,则 ,
所以 ,
所以 ,即 ....................................................................................12分
(二)选考题:共10分.请考生在22、23题中任选一题作答,如果多做,则按所做的第一题计分.
选修4-4:坐标系与参数方程
22.(10分)在直角坐标系 中,已知直线 的方程为 .以 为极点, 轴正半轴为极轴
建立极坐标系,曲线 的极坐标方程为 .
(1)求直线 的极坐标方程和曲线 的直角坐标方程;
(2)射线 与曲线 和直线 分别交于点 ,点 是曲线 上一点,求 面积的最大
值.
【详解】(1)将 , 代入 得: ,
,即 ,
直线 的极坐标方程为 ;......................................................................................2分
,
,即 , 曲线 的直角坐标方程为 ........................................4分
(2)由 得: ;由 得: ;
;.........................................................................................................6分
由 知:射线 所在直线方程为: ,即 ,...........................................7分
设 ,
点 到直线 的距离 ,其中 ,..9分
面积的最大值为 ....................................................................10分
选修4-5:不等式选讲
23.(10分)已知函数 .
(1)求不等式 的解集;
(2)若 恒成立,求 的取值范围.
【详解】(1)当 时,不等式化为 ,解得 ;............................................1分
当 时,不等式化为 ,恒成立;................................................................................2分
当 时,不等式化为 ,解得 ,.........................................................3分
综上所述,原不等式的解集为 ...........................................................................................5分
(2)因为 ,....................................................7分
所以 恒成立等价于 ,解得 或 ,...................................9分故 的取值范围为 ..................................................................................................10分