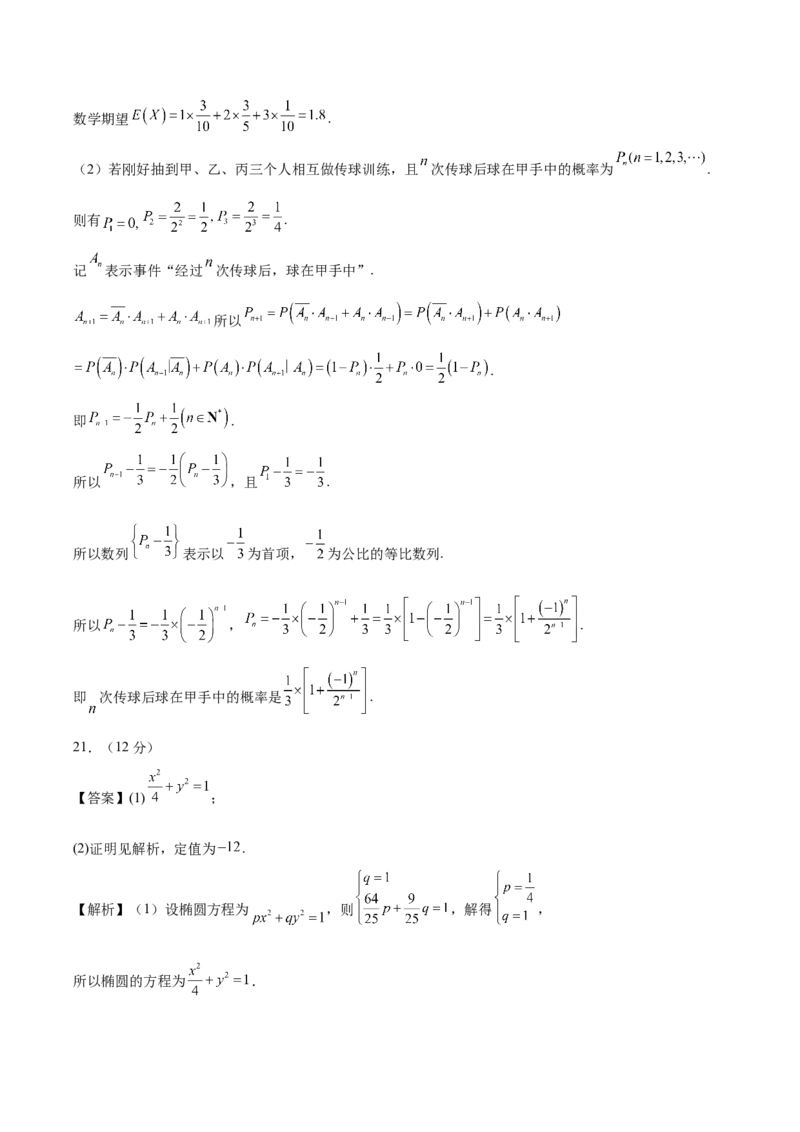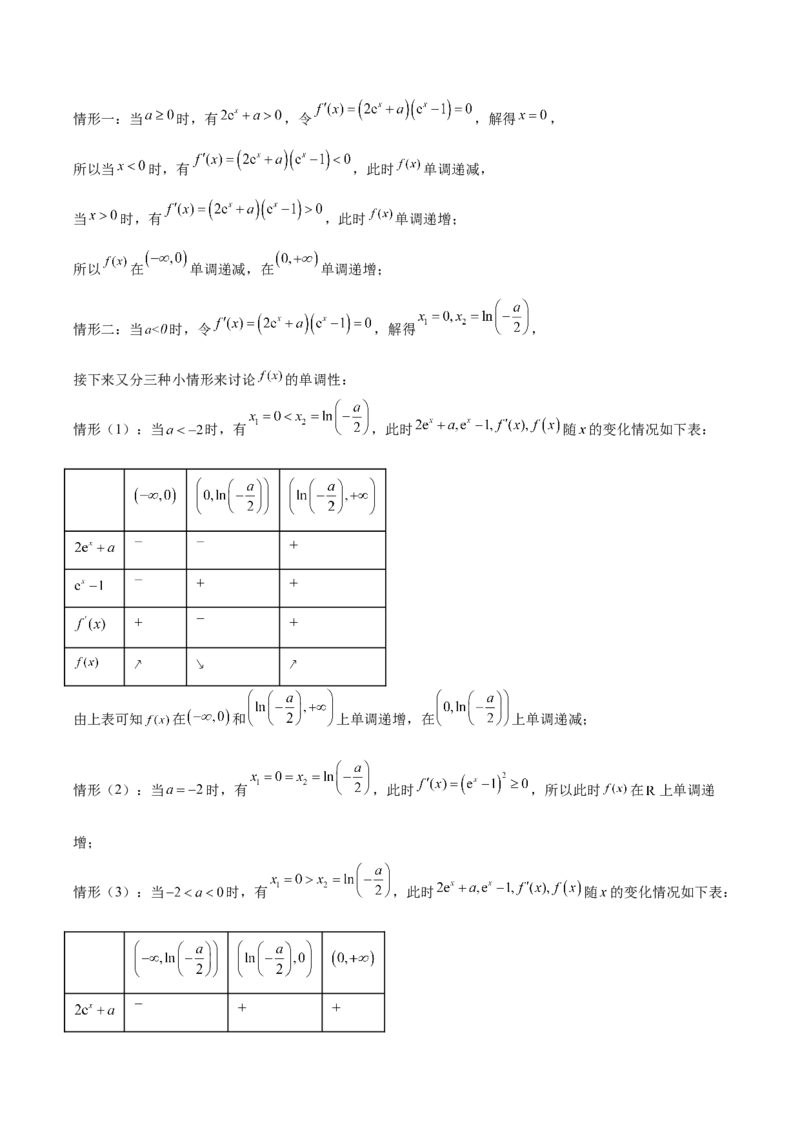文档内容
【赢在高考·黄金8卷】备战2024年高考数学模拟卷(新高考七省专用)
黄金卷02·参考答案
(考试时间:120分钟 试卷满分:150分)
第 I 卷(选择题)
一、单项选择题:本题共8小题,每小题5分,共40分,在每小题给出的四个选项中,只有一项是符合要
求的。
1 2 3 4 5 6 7 8
A D C C D B C C
二、多项选择题:本题共4小题,每小题5分,共20分,在每小题给出的四个选项中,有多项符合题目的
要求,全部选对的得5分,部分选对的得2分,有选错的得0分。
9 10 11 12
BCD ABD AC AC
第 II 卷(非选择题)
三、填空题:本题共4小题,每小题5分,共20分。
13.112 14. 15. 16.
四、解答题:本题共6小题,共70分,解答应写出必要的文字说明、证明过程及验算步骤。
17.(10分)
【答案】(1)
(2)
【解析】(1)因为 ,所以由正弦定理可得 .
又 ,所以 .
因为 ,所以 .
又 ,所以 , .(2) 的面积 ,则 .
由余弦定理: ,得 ,
所以 ,故 的周长为 .
18.(12分)
【答案】(1)证明见解析
(2) ,
【解析】(1)由 可得 ,
又 ,可得 为定值,
所以数列 是以3为首项,3为公比的等比数列.
(2)由(1)可知, ,可得 ,
即数列 的通项公式为
所以数列 的前 项和为
.
即 .
19.(12分)
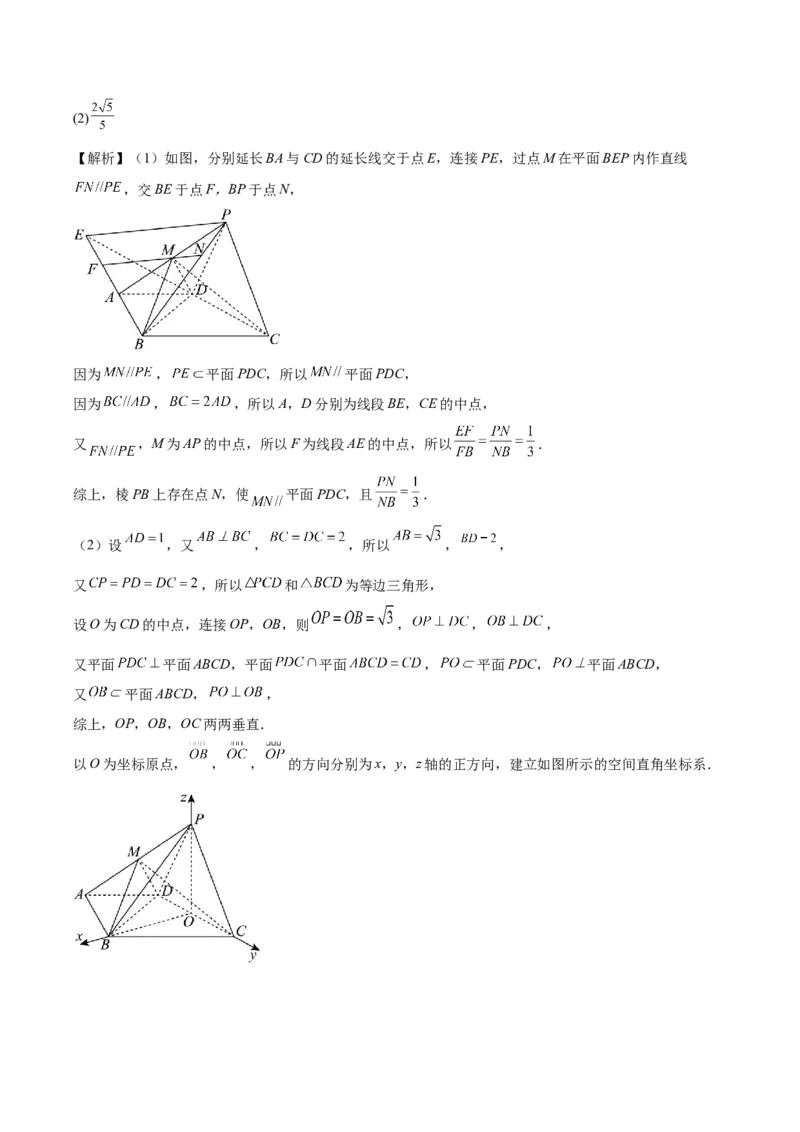
【答案】(1)棱PB上存在点N, ;(2)
【解析】(1)如图,分别延长BA与CD的延长线交于点E,连接PE,过点M在平面BEP内作直线
,交BE于点F,BP于点N,
因为 , 平面PDC,所以 平面PDC,
因为 , ,所以A,D分别为线段BE,CE的中点,
又 ,M为AP的中点,所以F为线段AE的中点,所以 .
综上,棱PB上存在点N,使 平面PDC,且 .
(2)设 ,又 , ,所以 , ,
又 ,所以 和 为等边三角形,
设O为CD的中点,连接OP,OB,则 , , ,
又平面 平面ABCD,平面 平面 , 平面PDC, 平面ABCD,
又 平面ABCD, ,
综上,OP,OB,OC两两垂直.
以O为坐标原点, , , 的方向分别为x,y,z轴的正方向,建立如图所示的空间直角坐标系.则 , , , , , ,
, , ,
设平面MDC的法向量为 ,
则 即 可取 ,
设平面MDB的法向量为 ,
则 即 可取 ,
所以 ,
故二面角 的正弦值为 .
20.(12分)
【答案】(1)分布列见解析,数学期望为
(2)① , , ;② ,
【解析】(1) 的所有可能取值为1,2,3.则
; ; .
所以随机变量 的分布列为:
1 2 3数学期望 .
(2)若刚好抽到甲、乙、丙三个人相互做传球训练,且 次传球后球在甲手中的概率为 .
则有 .
记 表示事件“经过 次传球后,球在甲手中”.
所以
.
即 .
所以 ,且 .
所以数列 表示以 为首项, 为公比的等比数列.
所以 , .
即 次传球后球在甲手中的概率是 .
21.(12分)
【答案】(1) ;
(2)证明见解析,定值为 .
【解析】(1)设椭圆方程为 ,则 ,解得 ,
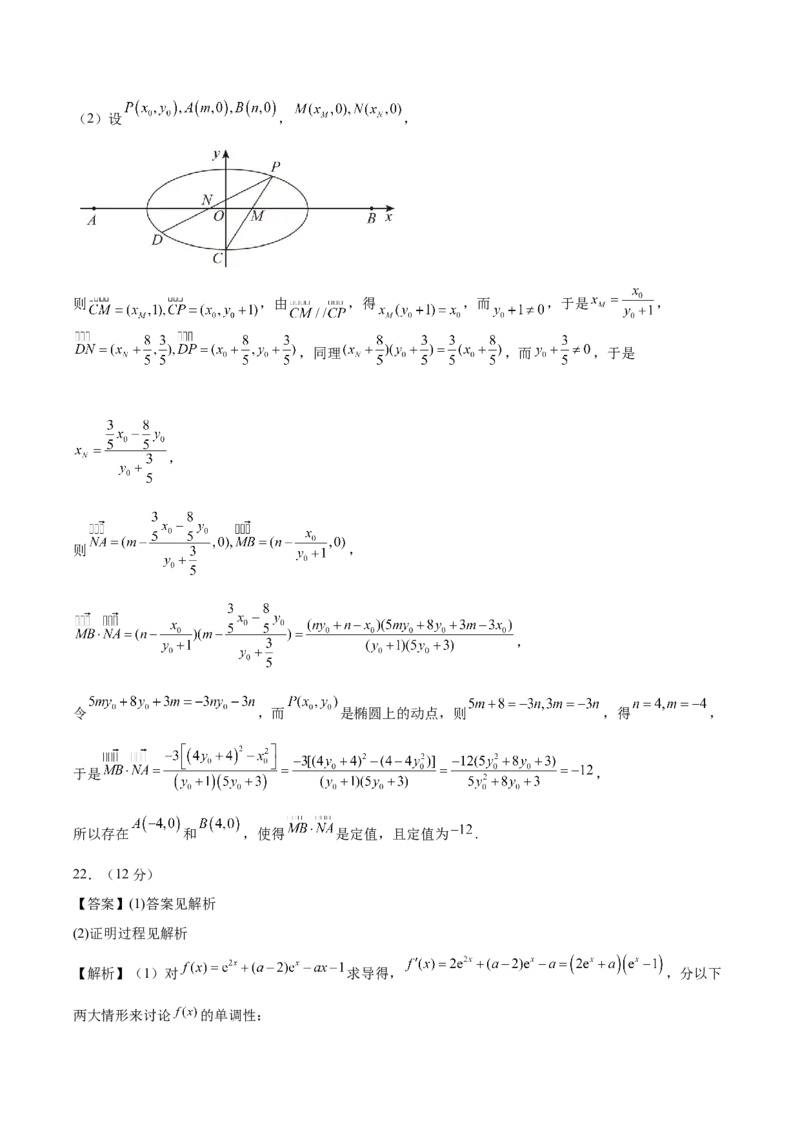
所以椭圆的方程为 .(2)设 , ,
则 ,由 ,得 ,而 ,于是 ,
,同理 ,而 ,于是
,
则 ,
,
令 ,而 是椭圆上的动点,则 ,得 ,
于是 ,
所以存在 和 ,使得 是定值,且定值为 .
22.(12分)
【答案】(1)答案见解析
(2)证明过程见解析
【解析】(1)对 求导得, ,分以下
两大情形来讨论 的单调性:情形一:当 时,有 ,令 ,解得 ,
所以当 时,有 ,此时 单调递减,
当 时,有 ,此时 单调递增;
所以 在 单调递减,在 单调递增;
情形二:当 时,令 ,解得 ,
接下来又分三种小情形来讨论 的单调性:
情形(1):当 时,有 ,此时 随 的变化情况如下表:
由上表可知 在 和 上单调递增,在 上单调递减;
情形(2):当 时,有 ,此时 ,所以此时 在 上单调递
增;
情形(3):当 时,有 ,此时 随 的变化情况如下表:由上表可知 在 和 上单调递增,在 上单调递减.
综上所述:当 时, 在 和 上单调递增,在 上单调递减;
当 时, 在 上单调递增;
当 时, 在 和 上单调递增,在 上单调递减;
当 时, 在 上单调递减,在 上单调递增.
(2)因为 ,所以由题意 ,
又因为 在区间 上存在唯一零点 ,
所以存在唯一的 ,有 ,化简得 ,
若要证明 ,则只需 ,即只需 ,
不妨设 ,求导得 ,
令 ,继续求导得 ,
所以当 时, 单调递增,
所以 ,
所以当 时, 单调递增,所以 ,
即当 时,有不等式 成立,
综上所述:若 在区间 上存在唯一零点 ,则 .