文档内容
2024 年全国高考名校名师联席命制
数学(文)押题卷(一)
题号 1 2 3 4 5 6 7 8 9 10
答案 A D D D A C B B C D
题号 11 12 13 14 15 16
答案 C D y2 x
6 3 = 3
一、整体情况
本套试卷覆盖了高中数学的主干内容,重视对数学思想方法的考查,试题稳定,主要
体现在试卷的题量、布局上. 从布局上看,具有起点低、结尾高,入手容易、深入难等特
点,梯度非常明显.整套试卷做题顺畅度较高,难度系数为 . ,平均得分 . 分,得分
0 6 112 7
分及以上占 %, 分占 %, 分占 . %.各题型内部得分基本呈按
130 5 120~130 21 110~120 37 6
题号增大不断递减的趋势.
二、选填题部分
注重基础,难度适中.选择题平均得分 . 分,失分较严重的情况主要集中在第 、
48 9 9
、 题.第 题考查三角函数的图像与性质;第 题考查双曲线的几何性质,是热门考
11 12 9 11
点;第 题考查三棱锥的外接球.填空题平均得分 . 分,第 题为解三角形与向量的
12 15 3 16
结合,关系转化难度较大,综合性较强.
三、解答题部分
每道解答题都是分层设问,难易搭配适当,控制了较难题的比例,整体上不偏难.试卷
注重基础,但完全答对则需具备扎实的功底.第 题考查函数极值、极值点以及利用导数
21
判断函数的单调性、不等式的证明,难度较大.
1.A 【押考点】复数的模及四则运算 共轭复数的概念
,
【深度解析】因为z 2 所以z 1-i 1-i 1 1 所以z 1 1 所以
(1+i) =1-i, = 2 = =- - i, =- + i,
(1+i) 2i 2 2 2 2
( ) ( )
2 2
z 1 1 2.故选A.
| |= - + =
2 2 2
一题多解
z z |1-i| |1-i| 2.故选 .
| |=| |= ( )2 = = A
| 1+i | |2i| 2
2.D 【押考点】集合的交集运算及真子集的个数
【深度解析】因为A x N x B 所以A B 所以集
={ ∈ |3- ≥0}={0,1,2,3}, ={0,1}, ∩ ={0,1},
合A B的真子集的个数为 2 .故选D.
∩ 2 -1=3
方法速记 若一个集合中有n个元素,则这个集合有 n 个子集, n 个真子集, n
2 2 -1 2 -1
个非空子集, n 个非空真子集.
2 -2
3.D 【押考点】古典概型的概率计算
【深度解析】用 甲 乙 表示甲 乙两同学的选择结果 记体操 跳水 羽毛球分别为A B
( , ) 、 , 、 、 , ,
C 则两人选择比赛项目的情况有 A B A C B B B C C B C C 共
, ( , ),( , ),( , ),( , ),( , ),( , ), 6
种 其中甲 乙所选的比赛项目相同的情况有 B B C C 共 种 故所求概率P 2
, 、 ( , ),( , ), 2 , = =
6
1 .故选D.
3
4.D 【押考点】根据函数零点求参数取值范围m x2 x m
【深度解析】因为f x x -2 + 且f x 有两个零点 所以方程 x2 x m
( )= + x -2= x , ( ) , -2 + =0
{m
在 上有两个不同的解 所以 >0, 解得 m .故选D.
(0,+∞) , Δ m 0< <1
=4-4 >0,
一题多解 由f(x) 得m x x2 (x )2 ,因为 f(x)有两个零点,所以直线
=0 =2 - =- -1 +1
y m与函数y (x )2 ,x 的图像有两个交点.函数y (x )2 ,x 的图像如
= =- -1 +1 >0 =- -1 +1 >0
图,由图可知 m .故选 .
0< <1 D
5.A 【押考点】三角恒等变换
5π α
( ) tan -tan
【深度解析】因为 5π α 4 1 解得 α 所以 α
tan - = = - , tan = 2, sin 2 =
4 5π α 3
1+tan tan
4
α α α
2sin cos 2tan 4 .故选A.
2α 2α= 2α=
cos +sin 1+tan 5
6.C 【押题型】线面 面面位置关系的判定
、
【深度解析】对于 只能得到n垂直于平面α内与m平行的直线 故A错误
A, , ;
对于 由面面垂直的性质定理得当 m α 时 m β 当 m α 时 m 与 β 不垂直 故 B
B, ⊂ , ⊥ , ⊄ , ,
错误
;
对于 由线面平行的性质定理知C正确
C, ;
对于 只有当m n为异面直线时 α β 故D错误.故选C.
D, , , ∥ ,
7.B 【押考点】导数的几何意义
a ( a )
【深度解析】由f 得切点为M 代入x y 解得a 所以f x x2
(1)= , 1, , +2 -3=0, =2, ( )= +
2 2
b
b x 所以f′ x x 所以f′ b 1 解得b 5 .所以a b .故选B.
ln , ( )=2 + x , (1)=2+ =- , =- +2 =-3
2 2
8.B 【押考点】平面向量数量积的应用
【深度解析】因为a b c 0 所以a b c 所以a2 b2 c2 b c.又a b c是单位
-2 +2 = , =2 -2 , =4 +4 -8 · , ,
向量 则a2 b2 c2 故b c 7 .所以 b c 2 b2 b c c2 7 3 所以 b
, = = =1, · = | -2 | = -4 · +4 =1- +4= , | -
8 2 2
c 6.因为a b c b c b c b2 c2 b c 21 3 所以
2 |= ·( -2 )= (2 -2 )·( -2 )= 2 +4 -6 · =6- = ,
2 4 4
a b c
a b c ·( -2 ) 6.故选B.
cos〈 , -2 〉= a b c =
| || -2 | 4
一题多解 因为a b c 0,所以 a b c. 因为 a,b,c 是单位向量,所以设 a
-2 +2 = =2 -2 =
( , ),b (x ,y ),c (x ,y ),则x2 y2 ,x2 y2 ,( , ) ( x x , y y ),解得
1 0 = 1 1 = 2 2 1+ 1=1 2+ 2=1 1 0 = 2 1-2 2 2 1-2 2
( ) ( )
x 1 ,x 1 ,y y 15,取 b 1 , 15 ,c 1 , 15 ,则 b c
1= 2=- 1 = 2 =± = = - -2 =
4 4 4 4 4 4 4
( ) ( )
3 , 15 . 因为 a·(b c) ( , )· 3 , 15 3 , b c 6,所以
- -2 = 1 0 - = | -2 | =
4 4 4 4 4 2
3
a·(b c)
〈a,b c〉 -2 4 6.故选 .
cos -2 = a b c = = B
| || -2 | 6 4
1×
29.C 【押考点】三角函数的图像与性质 三角函数的图像变换
,
( )
【深度解析】因为f x ωx ωx ωx π 所以将f x 的图像向左平移π个
( )=sin -cos = 2sin - , ( )
4 4
[ ( ) ] ( ω )
单位长度后 得到函数h x ω x π π ωx π π 的图像 再把
, ( )= 2sin + - = 2sin + - ,
4 4 4 4
( ω )
所得图像上点的横坐标缩短为原来的一半 得到函数g x ωx π π 的图
, ( )= 2sin 2 + -
4 4
( ) ω
像.因为点 π 是g x 图像的一个对称中心 所以 ω π π k k Z 解得ω
,0 ( ) , π + - = π, ∈ , =
2 4 4
4 k 1 k Z 又ω 所以ω的最小值为 1 .故选C.
+ , ∈ , >0,
5 5 5
本题错选率为 . %,易错选项均匀分布,出错的原因在于学生对于三
33 8
角函数的图像变换不熟练,导致失分.
10.D 【押题型】构造函数比较指数式 对数式的大小
、
x
【深度解析】因为 a 1 ln e b 3ln2 ln8 c 2ln3 ln9 所以令g x ln 则 a
= 2 = 2 , = = 2 , = = 2 , ( )= x2 , =
e e 64 8 81 9
x
g b g c g .g′ x 1-2ln 当x 时 g′ x 所以函数g x
(e), = (8), = (9) ( )= x3 , ∈( e,+∞) , ( )<0, ( )
在 上单调递减.又 所以g g g 即c b a.故选D.
( e,+∞) e (8)> (9), < <
11.C 【押考点】双曲线的定义及余弦定理
【深度解析】由双曲线的对称性 设点 P 在第一象限 如图. 因为
, ,
PQF 是等边三角形 所以 PQ PF QF 所以 PF PF
△ 2 , | |=| 2|=| 2|, | 1|-| 2|=
QF a QF QF a
提示:双曲线的定义
则
QF
| 1|=2 ,| 2|-| 1| =2 ( ), | 2| =
a 则 PF a PF a. 在 PF F 中 由余弦定理可得
4 , | 1 | =6 ,| 2 | =4 △ 1 2 ,
F PF |
PF
1|
2
+|
PF
2|
2
-|
F
1
F
2|
2
36
a2
+16
a2
-4
c2
1 整理得
cos∠ 1 2= PF PF = a2 = ,
2| 1|| 2| 48 2
c2 a2 所以b2 c2 a2 a2 解得a 所以实轴长为 .故选C.
=7 , = - =6 =6, =1, 2
本题错选率为 . %,易错选项均匀分布,在解题时需要根据题设作
41 2
图,找出三角形的边长及角度关系,利用余弦定理解三角形,部分学生未能利用双曲线
定义找到QF 的长度,所以失分.
2
12.D 【押题型】线面垂直的判定和性质 三棱锥的外接球
,
【深度解析】如图 设 BCD的中心为O′ 取BD的中点
, △ ,
F 连接AF CF OB O′B AO OO′ 则AF BD CF BD 而
, , , , , , , ⊥ , ⊥ ,
AF CF F 所以 BD 平面 ACF 易求得 AF CF .
∩ = , ⊥ , = = 3
因为AC 所以 AFC 3+3-9 1 则 AFC
=3, cos∠ = =- , ∠ =
2× 3× 3 2
°.在平面AFC 中 过点 A 作 CF 的垂线 与 CF 的延长线交于点 E 由 BD 平面
120 , , , ⊥
ACF 得BD AE 又 CF AE CF BD F 则 AE 平面 BCD 过点 O 作 OG AE 于点
, ⊥ , ⊥ , ∩ = , ⊥ , ⊥
G 则四边形O′EGO是矩形.因为 AFC ° 所以 AFE °.因为AF 所以AE
, ∠ =120 , ∠ =60 = 3, =
3 EF 3.又O′B BC ° 2 2 3 所以O′F 1 O′B 3.设球O的半径为R
, = = sin60 × = , = = ,
2 2 3 3 2 3
( ) 2 ( ) 2
OO′ x 则由OO′2 O′B2 OB2 OA2 AG2 GO2 得x2 4 R2 3 x 3 3
= , + = , = + , + = , - + + =
3 2 3 2R2 解得R2 7 所以球O的半径为 21.故选D.
, = ,
3 3
本题错选率为 . %,易错选项为 ,几何体的外接球为考试热点,同时
43 1 A
也是重难点,学生在解题时难以找到有效信息确定球心位置,造成错选.
13. 【押题型】简单的线性规划问题
6
【深度解析】作出约束条件表示的可行域 如图阴影部分 包含边界 所示.作出直线x
, ( ) -
y 并平移 由图可知 当直线经过点 时 z取得最大值 z .
3 =0 , , (0,-2) , , max=0-3×(-2)=6
14. 【押题型】对数的运算性质及换底公式的应用
3
【深度解析】由题知x y z
=log26, =log36, =log46,
则 1 3 1 1 3 1 .
x + y + z = + + =log62+3log63+log64=log6216=3
log26 log36 log46
15.y2 x 【押考点】抛物线的方程 直线与抛物线的位置关系
= ,
( p )
【深度解析】设过 F 的直线 l 的方程为 x my
,0 = +
2
p
m 与y2 px联立 可得y2 pmy p2 .
( ≠0), =2 , -2 - =0
2
设A x y B x y y y
( 1, 1), ( 2, 2), 1>0, 2<0,
则y y pm y y p2
1+ 2=2 , 1 2=- ,
y2 y2 p2m2 p2
则 AB x x p 1 2 p 4 +2 p pm2 p .
| |= 1+ 2+ = p+ p+ = p + =2 +2 =3
2 2 2
如图 过点A作AH x轴于点H
, ⊥ ,
根据抛物线的定义可得 MH AF
| |=| |,
AH AH
则 AMF | | | | AFH 3 AFH 6 AFH 2
tan∠ = MH = AF =sin∠ = ,∴ cos∠ = ,tan∠ = ,
| | | | 3 3 2
1 2 m2 .由 pm2 p 得p 1 故C的方程为y2 x.
∴ m = , =2 2 +2 =3 = , =
2 2
快解 如图,过点A作AH x轴于点H,根据抛物线的定义可得 MH AF ,
⊥ | |=| |
AH AH p
则 AMF | | | | AFH 3, AB 2 p ,
tan∠ = MH = AF =sin∠ = ∴ | |= 2 AFH=6 =3
| | | | 3 sin ∠
p 1 ,故C的方程为y2 x.
∴ = =
2
16.
3
思路导引
正弦定理
→AB·→AC
=
2
A
a
cos
B
=
b(
2-cos
A)
→
b 与 c 的关系 tan
→
b2
=
1
A
sin
辅助角公式
余弦定理 A →
a2
sin
A+
4cos
A=
5 →
a的最小值
→
a2
=
5-4c o
A
s
→
三角恒等变换 + 基本不等式
→
a的最小值
sin 数形结合
转化为两点连线斜率 a的最小值
→ →【押考点】两角和的正弦公式 利用正弦 余弦定理解三角形
, 、
【深度解析】因为a B b A 所以由正弦定理得 A B B A
cos = (2-cos ), sin cos =sin (2-cos ),
所以 A B B A B 即 A B B C 所以由正弦定理得
sin cos +sin cos =2sin , sin( + )= 2sin =sin ,
c b.
=2
A
由→AB
·
→AC
=
2
A
可得bc
cos
A
=
2cos
A ,
代入c
=2
b
,
可得b2
=
1
A
.由余弦定理可得a2
=
tan sin sin
A
b2
+
c2
-2
bc
cos
A
=
b2
+(2
b
)
2
-2
b
×2
b
cos
A
=5
b2
-4
b2
cos
A
=
5-4c o
A
s .
sin
A
解法一:由a2
=
5-4c o
A
s 得a2
sin
A
+4cos
A
=5,
sin
a4 A θ 其中 θ 4 当 A θ 时 a4取最小值 提示:
16+ sin( + )=5, tan = a2, sin( + )= 1 , 16+ 5(
a4 (A θ)为定值,且 a4 ,所以当 (A θ)最大时, a4最小 此时a
16+ sin + 16+ >0 sin + 16+ ),
取得最小值 a4 a 所以a的最小值为 .
, =9, = 3, 3
A ( ) A
解法 二: a2
=
5-4c o
A
s
,
设 A
= 2
α
∈ (0, π),
则 α
∈ 0,
π
,
则 5-4c o
A
s
=
sin 2 sin
2α 2α 2α 2α 2α 2α α α α α
5sin +5cos -(4cos -4sin ) 9sin +cos 9sin cos 9sin cos
α α = α α = α+ α≥2 α· α =
2sin cos 2sin cos 2cos 2sin 2cos 2sin
α α
3,
当且仅当9sin
α=
cos
α,
即
cos
2α
=9sin
2α时
,
等号成立
,
所以a的最小值为
3
.
2cos 2sin
A A
解法三:设m sin 1 sin 其中A
= A =- × , ∈(0,π),
-4cos +5 4 A 5
cos -
4
A A ( )
因为 sin sin -0 表示点P 5 与点 A A 连
= ,0 (cos ,sin )
A 5 A 5 4
cos - cos -
4 4
线的斜率 如图所示 当过点 P 的直线与半圆相切时 斜率最
, , ,
小 设切点为A 在 OAP中 OA OP 5 可得PA 3 所
, , Rt△ , =1, = , = ,
4 4
( )
以斜率的最小值为k APO 4 所以 m的最大值为 1 4 1 所以
PA=-tan∠ =- , - × - = ,
3 4 3 3
a2 所以a 即a的最小值为 .
≥3, ≥ 3, 3
本题错误率为 . %,涉及解三角形与平面向量的结合,题目中包含对
59 3
三角恒等变换、正余弦定理解三角形以及三角函数求最值的考查,综合性较强,难度
较大.
17.【押素材】数据的平均数 频率的计算 独立性检验的应用
, ,
【解】 由题意 甲公司平均月薪的估计值x . . . . . 千元
(1) , 甲=0 2×5+0 4×7+0 3×9+0 1×11=7 6( ),
乙公司平均月薪的估计值 x . . . . . .
乙=0 1×3+0 2×5+0 3×7+0 2×9+0 15×11+0 05×13=
. 千元
7 5( ),
因为x x 所以从平均月薪收入更高的角度,应选择甲公司. 分
乙< 甲, …………………… 4
(本题也可以从其他统计数据特征进行分析,只要利用统计思想分析合理,都视为正确)
设甲公司有n 人 则300 . 解得n .
(2) 1 , n =0 3, 1=1000
1
设乙公司有n 人 则400 . 解得n .
2 , n =0 2, 2=2000
2
则两公司员工月薪不低于 元的总人数为 . .
10000 1000×0 1+2000×0 2=500,1
故甲 乙两公司所有员工中 月薪不低于 元的频率为 500 . 分
、 , 10000 = 6 …………… 8
3000
2
由题意 K2 1000×(200×350-250×200) 2000 . . 分
(3) , = = ≈6 734>6 635, …………… 10
450×550×400×600 297
故有99%的把握认为 就业意愿与年龄结构有关 . 分
“ ” ………………………………… 12
18.【押考点】线面平行的判定 面面垂直的性质及等体积法
,
【证明】如图 取BB 的中点P 连接PE PF.
(1) , 1 , ,
E P分别为AB BB 的中点 EP AB .
∵ , , 1 ,∴ ∥ 1
EP 平面AB C AB 平面AB C EP 平面AB C . 分
∵ ⊄ 1 1, 1⊂ 1 1,∴ ∥ 1 1 ………………………… 2
又P F分别为BB CC 的中点 PF B C .
, 1, 1 ,∴ ∥ 1 1
PF 平面AB C B C 平面AB C PF 平面AB C .
∵ ⊄ 1 1, 1 1⊂ 1 1,∴ ∥ 1 1
EP PF P 平面EPF 平面AB C . 分
∵ ∩ = ,∴ ∥ 1 1 ……………………………………………… 4
又 EF 平面EPF EF 平面AB C . 分
∵ ⊂ ,∴ ∥ 1 1 ……………………………………………… 5
【解】连接CE. ABC为正三角形 CE AB.
(2) ∵ △ ,∴ ⊥
AA 平面ABC AA 平面A ABB 平面A ABB 平面ABC.
∵ 1⊥ , 1⊂ 1 1,∴ 1 1⊥
平面A ABB 平面ABC AB CE 平面ABC CE 平面A ABB . 分
∵ 1 1∩ = , ⊂ ,∴ ⊥ 1 1 ……………… 8
AB CE .又CC 平面A ABB 点F到平面A ABB 的距离为 . 分
∵ =2,∴ = 3 1∥ 1 1,∴ 1 1 3 … 10
又 S 1 V V 1 3.
∵ △ AEB 1 = 2 ×1×2=1,∴ 三棱锥B 1- AEF= 三棱锥F - AEB 1 = 3 ×1× 3= 3
3
故三棱锥B AEF的体积为 . 分
1- 3 ……………………………………………………… 12
19.【押考点】数列通项公式的求解 错位相减法求和
,
S
【解】 由a 2 n得 S na n.
(1) n+1= n 2 n- n=
因为
2
S
n-
na
n=
n
,
n
∈
N∗
,
所以
2
S
n +1-(
n
+1)
a
n +1=
n
+1,
两式相减并化简得 na
n=(
n
-
a 所以 n a na 两式相减得a a a
1) n +1+1, ( +1) n +1= n +2+1, n+ n +2=2 n +1,
所以数列 a 为等差数列. 分
{ n} …………………………………………………………… 4
当n 时 S a 所以a .
=1 ,2 1- 1=1, 1=1
设等差数列 a 的公差为d 因为a a d 所以d
{ n} , 5= 1+4 =9, =2,
所以a n 2n-1. 分
n=1+2( -1)= …………………………………………………………… 6
因为 b a a n 所以 b n n 所以b n n 分
(2) 4 n=( n+ n +1)·2 , 4 n=4 ·2 , n= ·2 ,…………………… 8
则T n=1×2+2×2 2 +…+ n ·2 n ,2 T n=1×2 2 +2×2 3 +…+ n ·2 n +1 ,
n
所以 - T n=2+2 2 +2 3 +…+2 n - n ·2 n +1 = 2-2
+1
- n ·2 n +1 =(1- n )·2 n +1 -2,
1-2
所以T (n-1)·2n+1+2. 分
n= ……………………………………………………………… 12
20. 思路导引 ( )根据题意设出直线l的方程,点A,B的坐标 椭圆E在点A,B处的切
2 →
联立方程
线方程 点M的坐标 根据直线l的斜率是否存在进行分类讨论 MF 与AB
→ → → 1
垂直【押题型】椭圆的标准方程 切线 双曲线的实轴及直线垂直问题
、 ,
ì ï a {
ï2 =2 2, a
【解】由题意得í 解得 = 2,
(1) ïï1 1 b
îa2 + b2 =1, =1,
2
x2
所以椭圆E的标准方程为 +y2=1. 分
2 ………………………………………………… 4
【证明】 (先依据题目条件判断直线l的倾斜情况,为设直线方程作准备)
(2)
当直线l的斜率为 时 A B分别为椭圆E的左 右顶点 此时切线平行无交点 故不符合
0 , , 、 , ,
题意.
由 知F 设直线l x ty A x y B x y
(1) 1(-1,0), : = -1, ( 1, 1), ( 2, 2),
x x x x
则椭圆E在点A处的切线方程为 1 y y 在点B处的切线方程为 2 y y . 分
+ 1 =1, + 2 =1 ……… 6
2 2
ìx x
ï
1 y y
ï + 1 =1,① y y y y y y
由í 2 得x 2( 2- 1) 2( 2- 1) 2( 2- 1)
ï ï x 2 x y y M=x 1 y 2- x 2 y 1 = ( ty 1-1) y 2-( ty 2-1) y 1 = y 1- y 2 =-2,
î + 2 =1,②
2
x ty
代入 得y 1+ 1 1+( 1-1) t 所以M t . 分
① M= y = y = , (-2,) ………………………………… 9
1 1
当t 时 直线AB的斜率不存在 直线MF 的斜率为 MF AB
=0 , , 1 0, 1⊥ ;
t
当t 时 直线AB的斜率为 1 直线MF 的斜率为 0- t 所以MF AB.
≠0 , t , 1 =-, 1⊥
-1-(-2)
综上 MF AB. 分
, 1⊥ ………………………………………………………………………… 12
本题平均得分 . 分,第一问考查椭圆的标准方程,第二问考查直线与
6 21
椭圆的位置关系,证明两条直线的位置关系,综合性较强.
21. 思路导引 ( )对f(x)求导 f′(x)的正负 f(x)的单调性
1 → →
( )对f(x)求导 x ,x 为f′(x) 的两根 x x ,x x 用x 表示x ,x 的取值范围
2 → 1 2 =0 → 1+ 2 1 2→ 2 1 2
f(x ) f(x ) 的表达式 利用导数求出 f(x ) f(x ) 对应函数的单调性 证得
→2 1 - 2 +3 → 2 1 - 2 +3 →
结论
【押题型】利用导数研究函数的单调性 极值点及不等式的证明
、
【解】当a 5 时 f x x2 x x 定义域为
(1) = ,( )= -5 +2ln , (0,+∞),
2
x2 x x x
则f′ x x 2 2 -5 +2 (2 -1)( -2). 分
( )=2 -5+ x = x = x …………………………………… 2
令f′ x 得x 1 或x
( )=0, = =2,
2
( 1 )
当x 0, 或x (2,+∞)时,f′(x)>0,所以f(x)单调递增;
∈ 2 ∈
( 1 )
当x ,2 时,f′(x)<0,所以f(x)单调递减. 分
∈ 2 …………………………………… 5
x2 ax
【证明】函数f x 的定义域为 f′ x 2( - +1) x .
(2) ( ) (0,+∞), ( )= x , >0
因为x x 是f x 的两个极值点 所以x x 是方程x2 ax 的两个不等的正实根
1, 2 ( ) , 1, 2 - +1=0 ,
{x x a
所以
1+ 2= ,
所以a 2 x x x 1 . 分
x 1 x 2=1,
>2,
2
< 1<1< 2< 2, 1=x
2
………………………………… 7( ) ( a )
所以 f x f x f 1 f x 1 2 1 x2 ax x
2( 1)-( 2)+3=2 x - ( 2)+3=2 x2 - x +2ln x -( 2-2 2+2ln 2)+3=
2 2 2 2
( ) ( )( )
2 x2 a x 2 x 2 x2 x 1 x 2 x 2 x2 x2 .
x2 - 2+2 2- x -6ln 2+3=x2 - 2+2 2+ x 2- x -6ln 2+3=- x2 + 2-3ln 2+1
2 2 2 2 2 2
分
………………………………………………………………………………………… 9
(原式对应函数求导比较复杂,所以利用换元法简化运算)
令t x2 g t 2 t t t
= 2, ( )=- t + -3ln +1(1< <2),
则g′ t 2 3
t2
-3
t
+2 (
t
-1)(
t
-2)
( )= t2 +1- t = t2 = t2 <0,
所以g t 在 上单调递减.
( ) (1,2)
又当t 时 g t 所以g t .
→1 , ( )→0, ( )<0
故 f x f x . 分
2( 1)-( 2)+3<0 ………………………………………………………………… 12
本题平均得分 . 分,第一问考查函数的单调性,大部分学生可以
5 57
拿分;第二问是证明不等式成立,需要通过换元、构造函数简化计算,部分学生想不清换
元法,导致丢分.
22.【押考点】极坐标方程与直角坐标方程 参数方程与普通方程的互化及参数的几何意义
、
【解】 因为曲线C的极坐标方程为ρ 2θ θ 所以ρ2 2θ ρ θ.
(1) sin =4cos , sin =4 cos
又x ρ θ y ρ θ 所以曲线C的直角坐标方程为y2 x.
= cos , = sin , =4
因为直线l的倾斜角为π且过点
(1,0),
3
ì
ïx 1 t
ï =1+ ,
2
所以直线l的参数方程为í t为参数 .
ï ( )
ïy 3t
î =
2
代入y2 x 得 t2 t . 分
=4 , 3 -8 -16=0 ………………………………………………………… 3
设点A B对应的参数分别为t t 则t t 8
, 1,2, 1+ 2= ,
3
t t
所以线段AB的中点M对应的参数为 1+ 2 4
= ,
2 3
( )
5 2 3
代入直线l的参数方程 得点M的直角坐标为 , . 分
, 3 3 ………………………… 5
一题多解 ( )因为曲线C的极坐标方程为ρ 2θ θ,所以ρ2 2θ ρ θ.
1 sin =4cos sin =4 cos
又x ρ θ,y ρ θ,所以曲线C的直角坐标方程为y2 x.
= cos = sin =4
因为直线l的倾斜角为π且过点( , ),所以直线l的方程为y (x ).
1 0 = 3 -1
3
{y2 x,
=4
由 消去y,化简得 x2 x . ……………………………………… 分
3 -10 +3=0 3
y (x ),
= 3 -1
x x
解得x ,x 1 ,所以M的横坐标x 1+ 2 5 ,
1=3 2= M= =
3 2 3
代入直线l的方程,得点M的纵坐标y 2 3,
M=
3
( )
所以点M的直角坐标为 5 ,2 3 . …………………………………………………… 分
5
3 3{x α
曲线C 的参数方程 =4+cos , α为参数 化成普通方程为 x 2 y2
(2) 1 y α ( ) ( -4) + =1,
=sin
所以曲线C 是以 为圆心 为半径的圆.
1 (4,0) ,1
因为O→N O→M 所以N
=3 =(5,2 3), (5,2 3),
则直线l 的方程为y k x . 分
1 = ( -5)+2 3 ………………………………………………… 8
因为直线l 与曲线C 有两个交点
1 1 ,
k
所以圆心 到直线l 的距离d |2 3- | 解得k 11 3.
(4,0) 1 = k2
+1
<1, >
12
( )
11 3
故直线l 的斜率k的取值范围是 ,+∞ . 分
1 12 …………………………………… 10
23.【押题型】绝对值不等式的解法 绝对值三角不等式的性质及基本不等式的应用
,
【解】由题知f x f x x x .
(1) ( )+(2 -1)= | +1|+|2 |-7
当x 时 原不等式可化为 x x 解得x 则 x
<-1 , -3 -8< , >-2, -2< <-1;
当 x 时 原不等式可化为 x x 解得x 则 x
-1≤ ≤0 , - -6< , >-3, -1≤ ≤0;
当x 时 原不等式可化为 x x 解得x 则 x .
>0 , 3 -6< , <3, 0< <3
综上 不等式f x f x x的解集是{x|-21
-1
( ) ( n m) ( p m) ( p n )
所以m n p m n p 1 1 1
+ + =( + + ) m+ n + p =3+ m+ n + m+ p + n + p ≥9,
当且仅当m n p 时取等号
= = =3 ,
此时 x m x n p x x 即 x
( +1+ )( +1- - )=( +4)( -5)≤0, -4≤ ≤5,
所以f x m f x n p 当且仅当m n p 且 x 时取等号. 分
( + )+( - - )≥2, = = =3 -4≤ ≤5 ……… 102024 年全国高考名校名师联席命制
数学(文)押题卷(二)
题号 1 2 3 4 5 6 7 8 9 10
答案 A B B B D A A D C C
题号 11 12 13 14 15 16
( ] [ ]
答案 B A x y 5 5 11
4 5 - +1=0 0, ∪ ,
12 6 12
一、整体情况
整体来看,试卷做题顺畅度较高,难度系数为 . ,平均得分 . 分,得分 分及
0 6 113 5 130
以上占 %, 分占 %, 分占 . %.各题型内部得分基本呈按题号增大
2 120~130 33 110~120 27 5
不断递减的趋势.
二、选填题部分
选择题平均得分 . 分,失分较严重的情况主要集中在第 、 、 题.第 题考查
49 6 10 11 12 10
求三棱锥外接球的表面积,几何体的外接球问题是学生的痛点;第 题考查求数列的前n
11
项和,思路是根据题设求解数列的通项公式,进而求和,但部分学生对其分析不清;第 题
12
中涉及函数图像的交点,需要分类讨论.填空题平均得分 . 分,失分主要集中在第 和
14 4 15
题,第 题考查曲线的公切线,第 题主要涉及三角函数中参数范围的求解,需要注
16 15 16
意端点值的取到问题.
三、解答题部分
此部分普遍反馈前 道题难度不大,但从得分情况来看,细节上扣分较多,运算要求比较
4
高,例如第 题,学生找不到化简方法,导致失分;第 题第二问,大部分学生得不到分数.
19 21
1.A 【押考点】集合的交集运算
【深度解析】因为A x Z x2 x x Z x B
={ ∈ | + -2≤0}={ ∈ |-2≤ ≤1}={-2,-1,0,1}, =(0,
所以A B .故选A.
+∞), ∩ ={1}
2.B 【押考点】复数的四则运算及模
【深度解析】因为z 2 2(1+i) 所以 z .故选B.
= = =1+i, | |= 2
1-i (1-i)(1+i)
一题多解
因为z 2 ,所以 z 2 |2| 2 .故选 .
= | |= = = = 2 B
1-i 1-i |1-i| 2
3.B 【押考点】平面向量平行的定义以及坐标运算
【深度解析】因为a b λ 所以a b λ .因为 a b a 所以 λ
=(2,1), =(-1, ), + =(1, +1) ( + )∥ , 1=2 +
解得λ 1 .故选B.
2, =-
2
4.B 【押风向】直线与圆的位置关系 充分 必要条件的判断
, 、
【深度解析】圆C的一般方程x2 y2 x y 化成标准方程为 x 2 y 2 所以圆
+ -2 -4 =0 ( -1) +( -2) =5,
C的圆心为C 半径r .若直线l x y a 与圆C有公共点 则圆心到直线的距
(1,2), = 5 : +2 + =0 ,
a
离d | +5| 解得 a .所以 a 是 直线l x y a 与圆C x2 y2
= ≤ 5, -10≤ ≤0 “-12≤ ≤0” “ : +2 + =0 : + -
5
x y 有公共点 的必要不充分条件.故选B.
2 -4 =0 ”5.D 【押题型】根据三视图求 阳马 的侧棱长
“ ”
【深度解析】设 阳马 为四棱锥 A BCDE 如图所示.由三视图得
“ ” - ,
AB BC CD BE AB 平面 BCDE 四边形 BCDE 是矩
=1, =1, = =2, ⊥ ,
形.因为BC BE 平面 BCDE 所以 AB BC AB BE 则 AC
, ⊂ , ⊥ , ⊥ , =
2 2 AE 2 2 AD 2 2 2 .故最长的
1 +1 = 2, = 1 +2 = 5, = 1 +1 +2 = 6
侧棱长为 .故选D.
6
6.A 【押考点】三角恒等变换
θ θ θ θ θ
θ cos
2
-sin
2
cos -sin 1-tan
【深度解析】因为 cos 2 2 2 2 2 1 解得
1+sin θ= ( θ θ ) 2 = θ θ = θ = 3 ,
cos +sin cos +sin 1+tan
2 2 2 2 2
θ
θ 2tan ( ) θ
1 所以 θ 2 4 所以 θ π tan +1 .故选A.
tan = , tan = θ = , tan + = θ=-7
2 2 2 3 4 1-tan
1-tan
2
一题多解 由题知 θ θ ,结合 2θ 2θ 可得 2θ θ ,解得
sin =3cos -1 sin +cos =1 5cos -3cos =0
( ) θ
θ 3 ( θ 舍去),则 θ 4 , θ 4 , θ π tan +1 .故选 .
cos = cos =0 sin = tan = tan + = θ=-7 A
5 5 3 4 1-tan
7.A 【押考点】古典概型
【深度解析】由题意 设 件正品的编号分别为a b c d 件次品的编号分别为A B 则从
, 4 , , , ,2 , ,
这 件产品中随机抽取 件的所有情况为 a A a B b A b B c A c
6 2 ( , ),( , ),( , ),( , ),( , ),( ,
B d A d B a b a c a d b c b d c d A B 共 种.设恰好
),( , ),( , ),( , ),( , ),( , ),( , ),( , ),( , ),( , ), 15
有 件正品为事件C 则事件C包含的情况有 a A a B b A b B c A c
1 , ( , ),( , ),( , ),( , ),( , ),( ,
B d A d B 共 种 则P C 8 .故选A.
),( , ),( , ), 8 , ( )=
15
8.D 【押题型】对数函数的单调性 不等式的性质
,
【深度解析】因为 b 所以 b a 当 a 时 得 b a 当a 时 得 a
loga >1, loga >loga , 0< <1 , 0< < <1; >1 , 1< <
b.故A错误.所以 a b 即ab a b 故B错误.当a b 时 a 1 b
( -1)( -1)>0, > + -1, =2, =3 , + b < +
1 故C错误.因为函数y x 1 在 上单调递减 在 上单调递增 所以a
a , = + x (0,1) , (1,+∞) , +
1 b 1 即a 1 b 1 故D正确.故选D.
a < + b , - b < - a ,
9.C 【押考点】双曲线的离心率
【深度解析】由题意得 矩形ABCD的宽为 c c 则长为 c 矩形
, 2 ( >0), 4 ,
ABCD与双曲线 E 如图所示 则 C c c .连接 CF 则 CF c
, ( ,2 ) 1, | 2| =2 ,
CF CF 2 F F 2 c.由双曲线的定义知 CF CF
| 1|= | 2| +| 1 2| =2 2 | 1|-| 2| =
a 即 c c c a 所以 c a 所以离心率 e
2 , 2 2 -2 =2( 2-1) =2 , ( 2-1) = , =
c
1 .故选C.
a = =1+ 2
2-1一题多解 由题意得,矩形ABCD的宽为 c(c ),则长为 c,矩
2 >0 4
形ABCD与双曲线 E 如图所示,则 C(c, c). 代入双曲线 E 的方
2
c2 c2
程,得 4 ,所以 c2(b2 a2) a2b2. 又因为 c2 a2 b2,所
a2 - b2 =1 -4 = = +
以(a2 b2)(b2 a2) a2b2,即 a4 b4 a2b2 ,等式两边同时除
+ -4 = -4 + -4 =0
a2 b2 b2
以a2b2,得 .设 t ,则 1 t ,即t2 t
-4 b2 +a2 -4=0 a2 = >0 -4 t + -4=0 -4 -
b2 c
,解得t 或t (不合题意,舍去),即 ,所以离心率e
4=0 =2+2 2 =2-2 2 a2 =2+2 2 = a =
b2
.故选 .
1+a2 = 1+2+2 2 =1+ 2 C
10.C 【押题型】正三棱锥的外接球的表面积
【深度解析】如图 取正三角形 BCD 的中心 P 连接 AP CP 则
, , , ,
AP 平面BCD 三棱锥A BCD的外接球球心O在AP上 连接
⊥ , - ,
OC.在正三棱锥 A BCD 中 因为 BC CD DB 所以 PC
- , = = =2, =
2 3.因为 AC 所以 AP AC2 PC2 4 15. 设
= 3, = - = 3- =
3 3 3
( )
2
OP h 由OC2 OA2 得 4 h2 15 h 解得h 1 .设球
= , = , + = - , =
3 3 2 15
O的半径为R 则R2 4 h2 27 所以三棱锥A BCD的外接球表面积S R2 27π.故
, = + = , - =4π =
3 20 5
选C.
11.B 【押考点】数列的通项公式 分组求和法
,
【深度解析】 a a n 当n 时 a a n 得当
∵ n +1+ n=4 +3 ①,∴ ≥2 , n+ n -1=4( -1)+3 ②,①-②
n 时 a a a 中奇数项成等差数列 偶数项成等差数列 公差均为 .
≥2 , n +1- n -1=4,∴ { n} , , 4 ∵
n
a 当n为奇数时 a a -1 n 当 n 为偶数时 a n a n .
1=1,∴ , n= 1+ ×4=2 -1; , n=4 +3- n +1=2 +2
2
S a a a a a a a a a a 5×(1+17) 5×(6+22) .故选B.
∴ 10=( 1+ 3+ 5+ 7+ 9)+( 2+ 4+ 6+ 8+ 10)= + =115
2 2
一题多解 a a n , a a (n ) ,a a , 数列{ a a }是
∵ n+ n +1=4 +3 ∴ n +2+ n +3=4 +2 +3 1+ 2=7 ∴ 2 n -1+ 2 n
以 为首项, 为公差的等差数列. S a a a a … a a 5×4 .
7 8 ∴ 10= 1+ 2+ 3+ 4+ + 9+ 10=5×7+ ×8=115
2
本题错选率为 . %,易错选项均匀分布,本题部分学生容易想到求解
43 1
数列的通项公式,而导致解题步骤烦琐,且对于数列的分类不清晰,导致失分.
12.A
思路导引 函数与方程的关系 {x,x a,
两函数的图像有两个交点 方程 4 ≥ 有两
等式的性质 → x +3= x a,x a
- +2 <
函数与方程的关系 {x,x a,
个不相等的实数根 函数y 4 与y ≥ 的图像有两个交
→ = x +3 = x a,x a
- +2 <
数形结合
点 两函数的图像 两函数的图像有两个交点时,a的值
→ →
【押题型】函数的图像及性质
{x x a
【深度解析】由题意得方程 x a 4 a 即 4 x a a , ≥ , 有两个不相
| - |-3= x - , x +3=| - |+ =
x a x a
- +2 , <
等的实数根.解x 4 得x 或x 因此一组斜率为 和斜率为 的直线组成的
= x +3 =4 =-1, -1 1折线与曲线y 4 有两个交点.在同一直角坐标系中 作出曲线y 4 和折线y
= x +3 , = x +3 =
{x x a
, ≥ , 如图.由图易得
x a x a
- +2 , <
当直线y x a与曲线y 4 相切时 两函数图像
① =- +2 = x +3 ,
有两个交点.由 4 x a得x2 a x 由判
x +3=- +2 +(3-2 ) +4=0,
别式Δ a 2 得a 1 或a 7 .
=(3-2 ) -16=0, =- =
2 2
当直线y x a过点A 时 两函数图像有两个交
② =- +2 (4,4) ,
点.由 a 得a .
-4+2 =4, =4
当直线y x a过点B 时 两函数图像有三个交点 由 a 得a .
③ =- +2 (-1,-1) , , 1+2 =-1, =-1
所以当两函数图像有两个交点时 a的值不可能是 故选A.
, -1,
本题错选率为 . %,学生易误选 ,题中涉及函数图像的交点,需要分
33 8 B
类讨论,利用数形结合的思想,但部分学生不能有机结合两种方法,导致题目解不出.
13. 【押题型】线性规划
4
【深度解析】根据约束条件画出可行域 如图中阴影部分 含边界 所示.画出直线 x
, ( ) 2 +
y 并平移 由图可知 当目标函数表示的直线经过点A 时 z取最小值 z
3 =0 , , (2,0) , , min=2×
.
2+3×0=4
14. 【押考点】直线与抛物线的位置关系以及抛物线的切线问题
5
【深度解析】由题意知 切线PM PN的斜率均存在 且不为 .
, , , 0
设切线PM的方程为x m y 将其代入y2 x 得y2 m y m
= 1( -1)-1, =4 , -4 1 +4 1+4=0,
由Δ m2 m 得m2 m 且点M的纵坐标为 m 则点M的横坐标
=16 1-4(4 1+4)=0, 1- 1-1=0, 2 1,
为m2 故M m2 m .
1, ( 1,2 1)
设切线PN的方程为x m y 同理可得m2 m N m2 m .
= 2( -1)-1, 2- 2-1=0, ( 2,2 2)
{m m
则m m 是方程m2 m 的两根 所以
1+ 2=1,
1, 2 - -1=0 , m m
1 2=-1,
所以 MN m2 m2 2 m m 2 m m 2 m m .
| |= ( 1- 2) +(2 1-2 2) = 5 ( 1+ 2) -4 1 2 =5
15.x y 【押考点】导数的几何意义以及利用导数求曲线的公切线
- +1=0
【深度解析】设曲线f x x上的切点为A x x x 曲线g x x上的
( )=2 ( 1,2 1)( 1>0), ( )=2+ln
切点为B x x x .因为 f′ x 1 g′ x 1 则公切线的斜率 k 1
( 2,2+ln 2)( 2>0) ( )= x, ( )= x , = x =
11 所以x x .因为公切线的方程为y x 1 x x 即y 1 x x
x , 2= 1 -(2+ln 2)= x ( - 2), = x +ln 2+1,
2 2 2
x
将 x x 代入公切线方程得 x 1 x 由 x x 得 x x
( 1,2 1) 2 1 = x +ln 2+1, 2= 1, ln 1- 1+1=
2
.令h x x x x 则h′ x 1 当 x 时 h′ x 当x 时 h′ x
0 ( )=ln - +1, >0, ( )= x -1, 0< <1 , ( )>0; >1 , ( )<
故函数h x 在 上单调递增 在 上单调递减 h x h 所以x
0, ( ) (0,1) , (1,+∞) , ( )max= (1)=0, 1=
x 故公切线方程为y x 即x y .
1, 2=1, = +1, - +1=0
本题错误率为 . %,本题考查曲线的公切线,学生对未给出切点的切
42 6
线类型的求解不熟练.
( ] [ ]
16. 5 5 11 【押考点】三角恒等变换 三角函数的图像及性质
0, ∪ , 、
12 6 12
( ) ( )
【深度解析】因为函数f x 3 ωx 1 ωx ωx π 在 内没有零
( )=2 sin + cos =2sin + (π,2π)
2 2 6
ì
ïω π k
( ) ï π+ ≥ π,
6
点 所以ωx π ω π ω π k k k Z 即í 解得 k
, + ∈ π+ ,2 π+ ⊆[ π, π+π], ∈ , ï -
6 6 6
ï ω π k
î2 π+ ≤ π+π,
6
k k
1 ω 5 k Z .由k 1 5 得k 7 又ω k Z 故k只可取 当k
≤ ≤ + ( ∈ ) - ≤ + , ≤ , >0, ∈ , 0,1, =
6 2 12 6 2 12 6
( ] [ ]
时 ω 5 当k 时 5 ω 11 故ω的取值范围为 5 5 11 .
0 ,0< ≤ ; =1 , ≤ ≤ , 0, ∪ ,
12 6 12 12 6 12
一题多解 ( ) ( )
f(x) 3 ωx 1 ωx ωx π ,令 f(x) ,得 ωx
= 2 sin + cos = 2sin + = 0 +
2 2 6
( k )
π k ,k Z,所以x 6 -1 π,k Z.设f(x)的最小正周期为T.因为f(x)在( , )
= π ∈ = ω ∈ π 2π
6 6
T ( k )
内没有零点,所以 π,解得 ω . 对 x 6 -1 π,k Z,取 k ,则 x
π≤ = ω 0< ≤1 = ω ∈ =1 =
2 6
5π,则5π 或5π ,解得ω 5 或ω 5 ;取k ,则x 11π,则11π ,解得
ω ω≤π ω≥2π ≥ ≤ =2 = ω ω ≥2π
6 6 6 6 12 6 6
( ] [ ]
ω 11.故 ω 5 或 5 ω 11,即ω的取值范围为 ,5 5 ,11 .
≤ 0< ≤ ≤ ≤ 0 ∪
12 12 6 12 12 6 12
17.【押素材】概率的计算 独立性检验
、
【解】 根据题目及表中数据 样本中男生近视的频率为30 3 所以估计这所学校男
(1) , = ,
70 7
3
生近视的概率为 . 分
7 …………………………………………………………………… 3
样本中 近视的女生有 名 女生近视的频率为10 1 所以估计这所学校女生近视的
, 10 , = ,
50 5
1
概率为 . 分
5 ……………………………………………………………………………… 6
因为抽取的男生有 人 女生有 人 列联表如下
(2) 70 , 50 ,2×2 :视力情况
性别 合计
近视 不近视
男生
30 40 70
女生
10 40 50
合计
40 80 120 分
………………8
2
根据列联表中的数据得K2 120×(30×40-40×10) . . 分
= ≈6 857>6 635, ……………… 10
70×50×40×80
所以有 %的把握认为近视与性别有关. 分
99 …………………………………………… 12
18.【押考点】空间中面面垂直的证明 三棱锥体积的计算
、
【证明】设AC与BD交于点N 连接PN 如图.
(1) , ,
四边形ABCD是菱形 N是BD的中点.
∵ ,∴
PB PD PN BD.
∵ = ,∴ ⊥
四边形ABCD是菱形 AC BD. 分
∵ ,∴ ⊥ ……………………… 2
PN AC N PN AC 平面PAC BD 平面PAC.
∵ ∩ = , , ⊂ ,∴ ⊥
又BD 平面PBD 平面PBD 平面PAC. 分
⊂ ,∴ ⊥ …………… 5
【解】在菱形ABCD中 BC BAD °
(2) ,∵ =2,∠ =120 ,
ABC和 ADC是等边三角形 AC .
∴ △ △ ,∴ =2
PC PA PC PA
∵ = 2 =2 2,∴ =2 2, =2,
PC2 PA2 AC2 PA AC.
∴ = + ,∴ ⊥
又 BD 平面PAC PA 平面PAC BD PA. 分
∵ ⊥ , ⊂ ,∴ ⊥ ……………………………………… 7
又 BD AC N BD AC 平面ABCD PA 平面ABCD.
∵ ∩ = , , ⊂ ,∴ ⊥
PA 平面PAD 平面PAD 平面ABCD.
∵ ⊂ ,∴ ⊥
平面PAD 平面ABCD AD 点C到AD的距离即为点C到平面PAD的距离.
∵ ∩ = ,∴
又 ADC是等边三角形 点C到平面PAD的距离为
∵ △ ,∴ 3,
M到平面PAD的距离h 3. 分
∴ = ……………………………………………………… 10
2
3
三棱锥M PAD的体积V 1 S h 1 1 AD PA 3 . 分
∴ - = · △ PAD· = × × × × = 3 ………… 12
3 3 2 2
19.【押题型】等差数列的证明 通项公式的求法以及与数列有关的恒成立问题
,
(1)
【证明】当n
≥2,
n
∈
N∗时
,
a
n=
S
n-
S
n -1,
则
2
S2n-2 S
n(
S
n-
S
n -1)+
S
n-
S
n -1=0, …… 2
分
化简得S S S S . 又S 等式 两边同除S S 得 1 1
n -1- n=2 n n -1 ① n≠0, ① n n -1, S
n
-S
n
=2,
-1
{ }
又 1 所以 1 是以 为首项 为公差的等差数列. 分
S =1, S 1 ,2 …………………………… 4
n
1
【解】由 得 1 n n 则S 1 分
(2) (1) S =1+( -1)×2=2 -1, n= n , …………………………… 6
n 2 -1
{ n
1, =1,
故a 分
n= 1 1 n . …………………………………………………………… 8
n - n , ≥2
2 -1 2 -3
a 1 1 2 由 na
λ
得λ 2
n +1
. 分
n +1= n - n =- n n , 2 n +1+ n <0, < n ……………… 9
2 +1 2 -1 (2 +1)(2 -1) 2 -1 2 +1
n
+1
令c 2
n= n ,
2 +1
n +2 n +1 n +1 n
则c c 2 2 2 (2 -1) 所以数列 c 单调递增. 分
n +1- n= n - n = n n >0, { n} …………… 11
2 +3 2 +1 (2 +1)(2 +3)
( 4 )
又c 4 故λ 4 所以实数λ的取值范围是 -∞, . 分
1= , < , 3 ………………………… 12
3 320. 思路导引 ( )四边形OABC为矩形 邻边垂直且对角线相互平分 直线OA,OC方
2 → →
与椭圆方程联立 中点坐标公式 点B在椭圆上
程 点A,C的坐标 点B的坐标 直线OA斜
→ → →
率k的方程 k OA , OC S
→ →| | | |→ 矩形OABC
【押考点】椭圆的标准方程 直线与椭圆的位置关系
,
ì ïc
6
ïa = ,
ï 3
【解】 由题知íc2 a2 b2 分
(1) ï = - , ………………………………………………………… 2
ï
ï1 8
îa2 + b2 =1,
3
解得
{a2
=9,
所以椭圆E的方程为
x2
+
y2
=1. 分
9 3 ………………………………………… 4
b2
=3,
由题意知 当直线OA的斜率为 或不存在时 矩形OABC不存在 不符合题意.
(2) , 0 , ,
分
……………………………………………………………………………………… 5
设直线OA的斜率为 k 则直线 OC 的斜率为 1 . 由椭圆的对称性 只需考虑 k 的
, - k , >0
情况.
不妨设点A x y 在第一象限 则点C x y 在第四象限.
( 1, 1) , ( 2, 2)
ìy kx
ïï = ,
k
由í
ïï x2 y2
消去y整理得
(1+3
k2
)
x2
=9,
解得x
1=
3
k2 ,
所以y
1=
3
k2
.
î + =1, 1+3 1+3
9 3
分
……………………………………………………………………………………… 7
ì
ïy 1 x
ï =- k , ( ) k
由í 消去y整理得 3 x2 解得x 3 所以y 3 .
ïx2 y2 1+k2 =9, 2= k2 , 2=- k2
ï 3+ 3+
î + =1,
9 3
(x x y y )
因为四边形OABC是矩形 线段AC的中点坐标为 1+ 2 1+ 2 所以线段OB的中点坐
, , ,
2 2
(x x y y )
标为 1+ 2 1+ 2 所以B x x y y .
, , ( 1+ 2, 1+ 2)
2 2
x x 2 y y 2
又因为点B在椭圆E上 所以( 1+ 2) ( 1+ 2)
, + =1,
9 3
即x2 x2 x x y2 y2 y y . 分
1+ 2+2 1 2+3( 1+ 2+2 1 2)=9 ………………………………………………… 9
又x2 y2 x2 y2 所以 x x y y .
1+3 1=9, 2+3 2=9, 2 1 2+6 1 2+9=0
k k
将x y x y 的值代入 得 18 54
1, 1, 2, 2 , k2 k2 - k2 k2 +9=0,
(1+3 )(3+ ) (1+3 )(3+ )
k
即 4 整理得k4 k2 解得k2 又k 所以k 分
k2 k2 =1, -2 +1=0, =1, >0, =1, …… 11
(1+3 )(3+ )
( ) ( )
此时A 3 3 C 3 3 B OA 3 2 OC 3 2 所以四边形OABC的面
, , ,- , (3,0),| |= ,| |= ,
2 2 2 2 2 2
9
积S OA OC . 分
=| |·| |= 2 ……………………………………………………………… 1221. 思路导引 对a分类讨论
( )导函数f′(x) 解f′(x) 得f(x)的单调递减区间,解
1 → <0
f′(x) 得f(x)的单调递增区间;
>0
( )思路一:
2
x -
x x - 令 x 2 - 1 = t
x ,x 是f(x) 的零点 a = e 1 , x 2 -x 1 = 2 1 1 1 用t表示x
1 2 → x - e x - → 1
1 1 1 1
→
x - x t的取值范围
3 1 2 ≤2→
x 的取值范围 a的取值范围
1 →
令x x p
思路二:x ,x 是 f(x)的零点 a(x x ) x 2 x 1 2- 1= 用 p 表示 x ,x ,a
1 2 → 2- 1 = e -e → 1 2
x x
3 1- 2≤2 p的取值范围 a的取值范围
→ →
【押题型】利用导数研究函数的单调性 求解参数取值范围
,
【解】 f x x ax a x 所以f′ x x a. 分
(1) ( )=e - + , ∈(-∞,+∞), ( )=e - ………………………… 2
当a 时 f′ x 恒成立 此时f x 在R上单调递增. 分
① ≤0 , ( )>0 , ( ) ………………………… 3
当a 时 令f′ x 得x a 令f′ x 得x a
② >0 , ( )<0, 0, >ln ,
所以f x 在 a 上单调递减 在 a 上单调递增. 分
( ) (-∞,ln ) , (ln ,+∞) …………………… 4
由题意及 可知 a 且f a ln a a a a a a
(2) (1) , >0, (ln )=e - ln + = (2-ln )<0,
所以 a 即a 2.又f f 2 a 所以 x x .
ln >2, >e (1)=e>0,(2)=e - <0, 1< 1<2, 2>2
x x x
由f x 1 ax a 得 1 a x 同理 2 a x
( 1)=e - 1+ =0, e = ( 1-1), e = ( 2-1),
x
两式相除得 x 2- x 1 2-1.
e =x
1-1
x
令t 2-1 t 则 t ( x 1-1)-( x 1-1) t 即 ( t -1)( x 1-1) t.
=x ( >1), e = , e =
1-1
t
等号两边同取自然对数 得 t x t 则x ln . 分
, ( -1)( 1-1)=ln , 1=1+t ……………………… 6
-1
x
又 x x 所以 x x 故t 2-1 .
3 1- 2≤2, 3( 1-1)≤ 2-1, =x ≥3
1-1
1 t
t 1- t -ln
令g t ln t 则g′ t 则g t 在 上单调递减.
( )=1+t -1 ( ≥3), ( )= ( t -1) 2 <0, ( ) [3,+∞)
因为g ln3 当t 时 g t 故 g t ln3 即 x ln3.
(3)=1+ , →+∞ , ( )→1, 1< ( )≤1+ , 1< 1≤1+
2 2 2
分
……………………………………………………………………………………… 8
x 1 x x x ( ]
又a e 令h x e x h′ x e( -2) 在 ln3 上恒成立 所以h x 在
=x
1-1
, ( )=x
-1
, >1, ( )=
(
x
-1)
2<0 1,1+
2
, ( )
( ]
ln3 上单调递减. 分
1,1+ ……………………………………………………………… 10
2
( ) é2 3e )
因为h ln3 2 3e 当x 时 h x 所以a的取值范围为êê ,+∞ .
1+ = , →1 , ( )→+∞, ëln 3
2 ln3
分
……………………………………………………………………………………… 12一题多解 ( )由题意可得a , x 1 ax x 2 ax ,即a(x x ) x 2 x 1.
2 >0 e - 1=e - 2 2- 1 =e -e
令x x p,则p ,x p x ,所以 x 1 ap ,等号两边同取自然对数,得x ap ,
2- 1= >0 2= + 1 e = p 1=ln p
e -1 e -1
ap
则x p.
2=ln p +
e -1
ap
又a e x 1 ,所以a e p -1 ,化简得 ap p ( p ) .
=x = ap ln = p +1+ln e -1 ①
1-1 e -1
ln p -1
e -1
p
因为 x x ,所以 ap p ( p ),代入 得 2 p,解得p .
3 1- 2≤2 2ln ≤2+ +2ln e -1 ① p ≤ ≥ln3
e -1
…………………………………………………………………………………… 分
6
p p p
又 a ( p ) p e -1,
ln = p +1+ln e -1 -ln = p +1+ln p
e -1 e -1
p (p ) p
令u(p) e -1,p ,则u′(p) -1 e +1 ,故u(p)在[ , )上单调递增,
= p ≥ln3 = p2 >0 ln3 +∞
[ )
则u(p) 2 , . ……………………………………………………………… 分
∈ +∞ 8
ln3
p [ )
令u e -1,则 a 1 u.令m(u) 1 u,u 2 , ,
= p ln = u +1+ln = u +1+ln ∈ +∞
ln3
u [ )
则m′(u) 1 1 -1 ,所以m(u)在 2 , 上单调递增,
=-u2 + u = u2 >0 +∞
ln3
[ )
则m(u) ln3+2 2 , ,则 a ln3+2 2 ,故a 2 3e.
∈ +ln +∞ ln ≥ +ln ≥
2 ln3 2 ln3 ln3
é )
所以a的取值范围为êê2 3e, . ………………………………………………… 分
ë +∞ 12
ln3
学生第一问可以拿分,在第二问中,可以将题设中两根代入得到等式关
系,但不会处理得到的式子,导致失分.
22.【押考点】直角坐标方程与极坐标方程的互化 线段长的最值
、
{x ρ θ ( )
【解】 因为x y 又 = cos ,所以ρ θ ρ θ 即 ρ θ π
(1) + -4=0, y ρ θ cos + sin -4=0, 2 sin + =4,
= sin , 4
( π)
故直线l的极坐标方程为ρsin θ+ =2 2. 分
4 ………………………………………… 5
由ρ2 2 得ρ2 ρ2 2θ
(2) = 2θ, + sin =2,
1+sin
又 {x = ρ cos θ ,ρ2 x2 y2 所以x2 y2 故曲线C的直角坐标方程是 x2 y2 . 分
y ρ θ = + , +2 =2, + =1 … 7
= sin , 2
φ φ φ α
设点Q φ φ 则点Q到直线l的距离d | 2cos +sin -4| | 6sin( + )-4 2|
( 2cos ,sin ), = = =
2 2
φ α
4 2- 6sin( + ) 其中 α .
, tan = 2
2
当φ α k π k Z时 d取得最小值4 2- 6.
+ =2 π+ , ∈ ,
2 2
4 2- 6
因为点P为直线l上的动点 所以 PQ 的最小值为 . 分
, | | 2 ……………………… 1023.【押考点】绝对值不等式的解法
【解】 当a 时 函数f x x x
(1) =2 , ( )= |2 -1|+| +1|,
{ {
{x x 1 x 1
所以f x 等价于 <-1, 或 -1≤ ≤ , 或 > ,
( )<8 x x 2 2
(1-2 )-( +1)<8 x x x x
(1-2 )+( +1)<8 (2 -1)+( +1)<8,
解得 8 x 或 x 1 或 1 x 8
- < <-1 -1≤ ≤ < < ,
3 2 2 3
( 8 8 )
所以不等式f x 的解集为 - , . 分
( )<8 3 3 …………………………………………… 5
当x 时 不等式显然成立 a R. 分
(2) =0 , , ∈ ……………………………………………… 6
当x 时 不等式f x x 即 1 a 1 .
≠0 , ( )≥| |, x - + x +1 ≥1
( ) ( ) ( )( )
又 1 a 1 1 a 1 a 当且仅当 1 a 1
x - + x +1 ≥ x - - x +1 = | +1|, x - x +1 ≤0
时 取得等号 分
, , …………………………………………………………………………… 8
所以 a 解得a . 分
| +1|≥1, ∈(-∞,-2]∪[0,+∞) ……………………………………… 9
综上 a的取值范围是(-∞,-2] [0,+∞). 分
, ∪ ………………………………………… 102024 年全国高考名校名师联席命制
数学(文)押题卷(三)
题号 1 2 3 4 5 6 7 8 9 10
答案 A D B C A C C D D A
题号 11 12 13 14 15 16
[ ]
答案 D B 2 16 5 8
-5 ,
2 3 2 3
1.A 【押考点】集合的交集运算
【深度解析】因为A x x B x x 所以A B x x .故选A.
={ |0< ≤1}, ={ |0≤ ≤2}, ∩ ={ |0< ≤1}
2.D 【押考点】诱导公式 同角三角函数的基本关系
、
【深度解析】因为 α α 1 所以 α 1 .又因为 α 所以 α
cos(π+ )=-cos = , cos =- sin <0, sin =
3 3
- 1-cos
2α
=- 1-
(
-
1
) 2
=-
2 2
,
所以
tan
α
=
sin
α
α=2 2
.故选D.
3 3 cos
一题多解
因为 α ,所以 ( α) α . 因为 ( α) 1 ,所以
sin <0 sin π+ = -sin >0 cos π+ =
3
( α) 2( α)
(
1
) 2
2 2.所以 α ( α) sin
(
π+
α)
sin π+ = 1-cos π+ = 1- = tan =tan π+ = ( α)=
3 3 cos π+
.故选 .
2 2 D
3.B 【押考点】共轭复数 复数的运算 模
, 、
【深度解析】因为z 所以z .因为z 所以z z
2=1-2i, 2=1+2i 1=4+3i, 1+ 2=(4+3i)+(1+2i)=5+
则 z z 2 2 .故选B.
5i, | 1+ 2|= 5 +5 =5 2
4.C 【押考点】平行直线间的距离
【深度解析】因为l l 直线l 的斜率为 所以b 2 1 -5 解得b 1 则
1∥2, 1 -2, ≠0, = b≠ , =- ,
1 - 5 2
l x y .所以两平行直线l l 间的距离d |10-(-5)| .故选C.
2:2 + +10=0 1,2 = =3 5
4+1
5.A 【押考点】根据三视图求组合体的体积
【深度解析】由几何体的三视图知 该几何体为圆锥和半球构成的组合体 其中上半部分圆
, ,
锥的高为 底面直径为 下半部分半球的直径为 .圆锥的体积V 1 2
3, 2, 2 1= ×(π×1 )× 3=
3
( )
3 半球的体积V 1 4 3 2 故该几何体的体积 V V V 2+ 3 .故
π, 2= × ×π×1 = π, = 1+ 2= π
3 2 3 3 3
选A.
6.C 【押题型】根据抽象函数的周期性求函数值
【深度解析】因为f x f x 所以f x f x .又因为f x f x 所以
( )= (- -4), (- )= ( -4) (- )+ ( -2)= 0,
f x f x 所以f x f x 即f x f x 所以f x f x
( -4)+( -2)=0, ( -2)+( )=0, ( -2)=- ( ), ( -4)=- ( -2)=
f x 所以函数f x 是周期为 的函数.在f x f x 中令x 得 f 即
( ), ( ) 4 (- )+( -2)=0 =1, 2 (-1)=0,
f 所以f f f .故选C.
(-1)=0, (2023)= (506×4-1)= (-1)=0
7.C 【押题型】几何概型 直线与双曲线的位置关系
、ìy kx
ïï = +1,
【深度解析】由
î
í
ïïx2
-
y2
=1,
消去y
,
得
(4-
k2
)
x2
-2
kx
-5=0
.由直线l与双曲线E的两支相
4
ì
ï4-
k2
≠0,
ïïΔ
k2
交 得í =80-16 >0,解得 k .因为k为区间 内的实数 所以由几何概型的概
, ï -2< <2 (0,4) ,
ï -5
î k2<0,
4-
率计算公式 得所求事件发生的概率P 2 1 .故选C.
, = =
4 2
8.D 【押题型】函数图像的判断
【深度解析】由题可知 函数f x 的定义域为 x x 关于原点对称 因为f x x
, ( ) { | ≠0}, , ( )=(e -
- x x 所以f x - x x x x - x x f x 所以函数f x
e )·ln | |, (- )=(e -e )·ln |- |=-(e -e )·ln | |=- ( ), ( )
( ) ( )
为奇函数 则其图像关于原点对称 排除选项 A,C 由于 f f 1 1
, , ; (1)= 0, = e- ·
2 e
1 排除选项B 另解:当 x 时, x , x - x ,所以f(x) ,排除选项 .故
ln <0, ( 0< <1 ln <0 e -e >0 <0 B)
2
选D.
9.D 【押考点】平面向量的线性运算 模的取值范围
、
【深度解析】设C为弦AB的中点 则 M→A M→B M→C .由于A B两点不重合 则点C在
, | + |=2| | , ,
圆O内.因为 MO 所以 M→C 提示:圆外一点 P 与圆上一点 Q 的距离
| | =2, | |∈(1,3)(
PQ [d r,d r],其中 d 为点 P 与圆心的距离,r 为圆的半径 则 M→A M→B
| |∈ - + ), | + | =
M→C .故选D.
2| |∈(2,6)
10.A 【押题型】等比数列的性质 前n项和
、
{ }
【深度解析】因为数列 a 是等比数列 设其公比为q 由题意得q 所以数列 1 是
{ n} , , ≠1, a
n
首项为 1 公比为 1 的等比数列 提示:等比数列的性质 .
a , q ( )
1
aq2
023
aq
2 023
S
2 023=
1(1-
q
)
=
1(
q
-1)
=200,
a
1 012=
a
1
q1 011
=10
.
1- -1
[ ( ) ]
{ } a
1
1-
1
q
2023
a q
1
2 022(
q2 023
-1)
设数列 1 的前 n 项和为 T 则 T 1 1 1
a n n, 2 023 = 1 = q -1 =a2 1 012 ·
1- q
a
1(
q2 023
-1)
S
2 023 200 .故选A.
q
-1
=a2
1 012
=
100
=2
一题多解 { }
设数列 1 的前 n 项和为 T ,则 T 1 1 1 1 … 1
a n n 2 023 = a + a + a + a + +a +
1 2 3 4 2022
( ) ( ) ( ) ( ) ( )
1 , T 1 1 1 1 1 1 … 1 1 1 1
a 2 2 023= a +a + a +a + a +a + + a + a + a +a =
2023 1 2023 2 2022 3 2021 2022 2 2023 1
(a a a a … a a ) S
2 1+ 2+ 3+ 4+ + 2 022+ 2 023 2 2 023 400 ,所以T .故选 .
a
1
a
2 023
= a2
1 012
=
100
=4 2 023=2 A
11.D 【押考点】导数的几何意义 利用导数求参数的取值范围
,
【深度解析】由题意得f′ x x2 ax b 设切点的坐标为 x f x 则切线的斜率为
( )= +2 + , ( 0, ( 0)),
f′ x 切线方程为 y f x f′ x x x . 因为切线过点 P 所以 f x
( 0), - ( 0)= ( 0)( - 0) (1,0), - ( 0)=
f′ x x 整理得 2 x3 a x2 ax 4 .
( 0)(1- 0), 0+( -1) 0-2 0- =0
3 3构造函数g x 2 x3 a x2 ax 4 则函数g x 有三个不同的零点.由三次函数
( )= +( -1) -2 - , ( )
3 3
的图像易知 函数g x 既存在极大值也存在极小值 且极大值与极小值异号.
, ( ) ,
g′ x x2 a x a x x a 则a 且g g a .
( )=2 +2( -1) -2 =2( -1)( + ), ≠-1, (1)· (- )<0
( )( ) ( )
5 a 1 a3 a2 4 所以 a 5 a a 2 .
- - + - <0, + ( -1)( +2) >0
3 3 3 3
又因为点P 在曲线y f x 的下方 所以f 即a 5 解得a .故选D.
(1,0) = ( ) , (1)>0, >- , >1
3
12.B
思路导引 椭圆的定义
P→F ·P→F F PF PF , PF ,a,b,c之间的关系
1 2=0→Rt△ 1 2 →| 1| | 2|
PF
结合| 1| [ , ]
PF ∈ 1 3
| 2| a,b之间的关系 离心率e
→ →
【押题型】椭圆的几何性质
【深度解析】因为P→F P→F 所以PF PF .设 PF m PF n 则m n a 提
1· 2=0, 1⊥ 2 | 1|= ,| 2|= , + =2 (
示:椭圆的定义 .在 F PF 中 m2 n2 c2 所以 mn m n 2 m2 n2 a2
) Rt△ 1 2 , + =4 , 2 =( + ) -( + )= 4 -
c2 b2 即mn b2.则
m n m2
+
n2
2
c2
.令
m
t 由|
PF
1| 得t 则
4 =4 , =2 n + m = mn = b2 n = , PF ∈[1,3], ∈[1,3],
| 2|
c2 c2 [ ] c2
t 1 2 .由于函数y t 1 在 上单调递增 则2 t 1 10 所以
+ t = b2 = + t [1,3] , b2 = + t ∈ 2, , b2 ∈
3
[ ] a2 a2 b2 c2 [ ] a2 [ ] b2 [ ]
5 即 - 5 所以 8 3 1 故离心率
1, , b2 -1= b2 = b2∈ 1, , b2 ∈ 2, ,a2∈ , ,
3 3 3 8 2
c b2 [ ]
e 2 10 .故选B.
= a = 1-a2 ∈ ,
2 4
13. 2 【押题型】分段函数求函数值
2
( ) ( ) ( )
【深度解析】由题意得f 7 f 3 f 1 - 2 1 2.
= = - =2 =
2 2 2 2
14. 【押考点】线性规划
-5
【深度解析】画出不等式组所表示的平面区域 如图中阴影部分 含边界 所示.令z x
, ( ) =2 -
y 则y x z.由图可知 当直线y x z经过点A时 其在y轴上的截距 z最大 则z最
, =2 - , =2 - , - ,
{x y {x
小 即z x y取得最小值 解 + -2=0,得 =-1,所以z .
, =2 - , x y y min=2×(-1)-3=-5
2 + -1=0 =3,
15.16 【押题型】三棱柱的外接球 三棱柱体积的最值
、
3【深度解析】由题知 直三棱柱ABC A B C 的底面是直角三角形 且
, - 1 1 1 ,
在 ABC中 BC AB.如图 将直三棱柱ABC A B C 补成长方
Rt△ , = 3 , - 1 1 1
体ABCD A B C D 则长方体ABCD A B C D 的外接球即为直三棱
- 1 1 1 1, - 1 1 1 1
柱ABC A B C 的外接球 且长方体的体对角线AC 的长为外接球的
- 1 1 1 , 1
直径.设AA h AB l 则 AC l BC l 所以 l 2 h2 即
1= , = , =2, = 3 , (2) + =4,
h2
l2 .所以直三棱柱 ABC A B C 的体积 V 1 l l h
=4- - 1 1 1 = · · 3 · =
4 2
( h2 ) ( h3 )
3l2h 3 h 3 h 其中h .
= 4- = 4 - , ∈(0,4)
2 2 4 2 4
解法一:设f h 3
(
h
h3 )
h 则 f′ h 3
(
3
h2 )
当 h 4 3时 f′
( )= 4 - , ∈(0,4), ( )= 4- , = ,
2 4 2 4 3
( ) ( )
h 当 h 4 3 时 f ′ h 当 h 4 3 时 f ′ h . 所以 f h 在
( )= 0; ∈ 0, , ( )>0; ∈ ,4 , ( )<0 ( )
3 3
( ) ( )
4 3 上单调递增 在 4 3 上单调递减 故当h 4 3时 f h 取得极大值也是最大
0, , ,4 , = ,( )
3 3 3
值16 即直三棱柱ABC A B C 体积的最大值为16.
, - 1 1 1
3 3
解 法 二: V2 3 ( h2 ) 2 h2 3 ( h2 ) ( h2 ) h2
= 4- · = 4- · 4- · ≤
4 4 2 4 4 2
é ê ( h2 ) ( h2 ) h2ù ú 3 ( ) 2 h2 h2
3 4- + 4- + 16 当且仅当 即h 4 3时取等号 所以
êê 4 4 2 úú = , 4- = , = ,
2 ë û 3 4 2 3
3
V 16 即直三棱柱ABC A B C 体积的最大值为16.
max= , - 1 1 1
3 3
[ ]
16. 5 8 【押考点】正弦型三角函数的性质
,
2 3
ω
【深度解析】因为ω 所以当 x π时 π ωx π π π.因为函数f x 在区间
>0, 0< < , - < - < - ( )
3 6 6 3 6
( ) ω ω
π 上不单调 所以 π π π 解得 ω .因为当2π x 时 2π π ωx π
0, , - > , >2 < <π , - < - <
3 3 6 2 3 3 6 6
( ) ( ω ) (
ω π 函数 f x 在区间 2π 上单调 所以 2π π ω π k π k
π - , ( ) ,π , - ,π - ⊆ π- , π+
6 3 3 6 6 2
ì ω
ï2π π k π
) ï - ≥ π- ,
π k Z 即í 3 6 2 其中k Z 解得 3 k 1 ω k 2 k Z 所以
( ∈ ), ï ∈ , - ≤ ≤ + ( ∈ ),
2 ï ω π k π 2 2 3
îπ - ≤ π+ ,
6 2
3 k 1 k 2 解得k 7 .又因为ω 所以k .当k 时 ω 2 当k
- ≤ + , ≤ >0, ∈{0,1,2} =0 ,0< ≤ ; =
2 2 3 3 3
[ ]
时 ω 5 当k 时 5 ω 8 .又因为ω 所以ω的取值范围是 5 8 .
1 ,1≤ ≤ ; =2 , ≤ ≤ >2, ,
3 2 3 2 3
17.【押题型】样本数据的中位数 平均数 方差在决策中的应用
、 、
【解】 A系列的综合打分结果从小到大排列为
(1) 76,79,81,84,86,86,88,92,93,95,
所以A系列综合打分的中位数为86+86 86 分
= ; ………………………………………… 2
2
B系列的综合打分结果从小到大排列为
75,80,80,83,85,87,90,92,93,95,
所以B系列综合打分的中位数为85+87 86. 分
= ………………………………………… 4
2A系列综合打分的平均数x 76+79+81+84+86+86+88+92+93+95 86
(2) A= = ,
10
方差s2A= 1
×[(-10)
2
+(-7)
2
+(-5)
2
+(-2)
2
+0
2
+0
2
+2
2
+6
2
+7
2
+9
2
]=
34.8.
……… 7
分
10
B系列综合打分的平均数x 75+80+80+83+85+87+90+92+93+95 86
B= = ,
10
方差s2B= 1
×[(-11)
2
+(-6)
2
+(-6)
2
+(-3)
2
+(-1)
2
+1
2
+4
2
+6
2
+7
2
+9
2
]=
38.6.
……… 10
分
10
由于A B两个系列综合打分的中位数相等 平均数相等 A系列综合打分的极差比B系
, , ,
列小
,
且s2A< s2B, 所以推广A系列种植更合适.
……………………………………… 12
分
18.【押题型】线线垂直的证明 线面垂直的证明 棱锥的体积
, ,
【证明】因为PA 平面ABCD AD 平面ABCD 所以PA AD.
(1) ⊥ , ⊂ , ⊥
因为DE PA PA DE AD
∥ , =2 =2 =4,
所以四边形ADEP为直角梯形 所以PE EA . 分
, =2 2, =2 2 …………………………… 3
在 PEA中 PE2 EA2 PA2 则PE EA
△ , + = , ⊥ ,
故 PEA °. 分
∠ =90 …………………………………………………………………………… 4
【证明】因为PA 平面ABCD AB 平面ABCD 所以PA AB.
(2) ⊥ , ⊂ , ⊥
在 PAB中 PB PA2 AB2 .
Rt△ , = + =2 5
在 PEB中 BE PE2 BE2 PB2 所以PE EB. 分
△ , =2 3, + = , ⊥ ……………………………… 6
由 知PE EA 又EA EB E EA EB 平面ABE 所以PE 平面ABE. 分
(1) ⊥ , ∩ = , , ⊂ , ⊥ ……… 8
一题多解 ( )因为PA 平面ABCD,PA 平面ADEP,所以平面ADEP 平面ABCD.
2 ⊥ ⊂ ⊥
因为四边形ABCD是正方形,所以AB AD.
⊥
因为平面ADEP 平面ABCD AD,AB 平面ABCD,所以AB 平面ADEP.
∩ = ⊂ ⊥
因为PE 平面ADEP,所以AB PE. ………………………………………………… 分
⊂ ⊥ 6
由( )知PE EA,又EA AB A,EA,AB 平面ABE,所以PE 平面ABE.………… 分
1 ⊥ ∩ = ⊂ ⊥ 8
【解】设三棱锥P ABE的高为h 则V 1 S h.
(3) - , 三棱锥P - ABE= × △ ABE×
3
由 得 PE 平面ABE 所以三棱锥P ABE的高即为PE.由 得 PE . 分
(2) , ⊥ , - (1) , =2 2 ……… 9
又在 ABE中 EA2 AB2 BE2 所以EA AB. 分
△ , + = , ⊥ ……………………………………… 10
8
S 1 AE AB 1 所以V 1 . 分
△ ABE= × × = ×2 2×2=2 2, 三棱锥P - ABE= ×2 2×2 2= 3 ……… 12
2 2 3
19.【押考点】正弦定理 余弦定理解三角形 基本不等式求最值
、 ,
b c
【解】 解法一:由题意及正弦定理得 C 2 +
(1) ,2cos = a ;
由余弦定理得
a2
+
b2
-
c2
2
b
+
c
整理得b2 c2 a2 bc 所以 A
b2
+
c2
-
a2
1 .
,2× ab = a , + - =- , cos = bc =-
2 2 2
2π
又 A 故A . 分
0< <π, = 3 …………………………………………………………………… 5
解法二:由题设可得 A C B C A C C 提示:三角形内角
,2sin cos =2sin +sin =2sin( + )+sin (
和 即 A C A C A C C 整理得 A C .
), 2sin cos =2sin cos +2cos sin +sin , (2cos +1)sin =0
2π
又因为 C 所以 A 1 .又 A 故A . 分
sin >0, cos =- 0< <π, = 3 ……………………………… 5
2
b c
解法三:由题意及正弦定理得 C 2 + 所以 a C b c a C c A c
,2cos = a , 2 cos =2 + =2 cos +2 cos + ,整理得 A c .
(2cos +1) =0
2π
又因为c 所以 A 1 .又 A 故A . 分
>0, cos =- 0< <π, = 3 ………………………………… 5
2
c c b c
解法一:因为B→D D→C 则A→D →AB B→D →AB B→C →AB →AC
(2) = b , = + = +c b =c b +c b ,
+ + +
( b c ) 2 b2 c2 bc
所以A→D2 →AB →AC →AB2 →AC2 →AB →AC.
= c + b +c + b = ( c + b ) 2 + ( c + b ) 2 +2 ( c + b ) 2 ·
因为 A→D →AB c →AC b BAC 2π 所以
b2c2 b2c2
2
b2c2
2π 整
| |=2,| |= ,| |= ,∠ = , 4= b c 2 + b c 2 + b c 2cos ,
3 ( + ) ( + ) ( + ) 3
理得b2c2 b c 2. 分
=4( + ) …………………………………………………………………… 9
因为b c 所以b c 1 bc 即 1 1 1 .
>0, >0, + = , b + c =
2 2
( ) ( c b ) c b
故b c 1 1 b c 当且仅当 b c
+ =2 b + c ( + )= 2 2+ b + c ≥4+2×2 b · c =8, = =4
时 等号成立.
,
故b c的最小值是8. 分
+ ………………………………………………………………… 12
c
解法二:因为B→D D→C 所以设BD kc CD kb k .
= b , = , = , >0
设 ADB θ
∠ = ,
在 ADB中 由余弦定理得c2 c2k2 ck θ
△ , =4+ -4 cos ①;
在 ADC中 由余弦定理得b2 b2k2 bk θ 即b2 b2k2 bk θ .
△ , =4+ -4 cos(π- ), =4+ +4 cos ②
b c 得bc2 cb2 b c bck2 b c .因为b c 所以bc bck2 .
①× +②× , + =4( + )+ ( + ) >0, >0, =4+ (∗)
在 ABC中 由余弦定理得 b c 2k2 b2 c2 bc 2π
△ , ( + ) = + -2 cos ,
3
bc
即 b c 2k2 b2 c2 bc 则k2 代入 整理得b2c2 b c 2. 分
( + ) = + + , =1- b c 2, (∗) =4( + ) ………… 9
( + )
所以b c 1 bc 即 1 1 1 .
+ = , b + c =
2 2
( ) ( c b ) ( c b ) c b
则b c 1 1 b c 当且
+ =2 b + c ( + )=2 2+ b + c =4+2 b + c ≥4+2×2 b · c =8,
仅当b c 时 等号成立.
= =4 ,
故b c的最小值是8. 分
+ ………………………………………………………………… 12
20.【押题型】抛物线的标准方程 几何性质 直线与抛物线的位置关系
、 ,
( λ ) λ
【解】 因为抛物线C y2 λx λ 的焦点为F 由题意得 解得λ
(1) : = ( >0) ,0 , -0=1, =
4 4
故抛物线C的标准方程为y2=4x. 分
4, ………………………………………………… 3
由 知F 由题意知直线l的倾斜角不为 .
(2) (1) (1,0), 0
因为M→F →AB 所以直线l 直线MF.
· =0, ⊥
当直线l的斜率不存在时 直线l的方程为x 点M为坐标原点O 此时直线MA MB的
, =1, , ,
斜率分别为 不满足 AMB ° 所以直线l的斜率存在. 分
±2, ∠ =90 , ……………………… 5
设直线l的方程为x my m 则直线MF的方程为x 1 y m .
= +1( ≠0), =- m +1( ≠0)设A x y B x y M x y 如图.
( 1, 1), ( 2, 2), ( 3, 3),
{x my
由 = +1,消去x得 y2 my
y2 x , -4 -4=0,
=4 ,
则Δ m2 y y m y y .
=16( +1)>0, 1+ 2=4 , 1 2=-4
{
x 1 y
由 =- m +1,消去x得 y2 4 y
, + m -4=0,
y2 x
=4 ,
所以y2 4 y .
3+ m 3-4=0 ①
y y y y
直线AM 的斜率为 3- 1 3- 1 4 同理可得直线 BM 的斜率为 4 提示:
x
3-
x
1
= y2
3
y2
1
=y
3+
y
1
, y
3+
y
2
(
-
4 4
AMB°,所以直线AM,BM的斜率都存在.
∠ =90 )
因为 AMB ° 所以 4 4 y2 y y y y y
∠ =90 , y y ·y y =-1, 3+( 1+ 2) 3+ 1 2=-16,
3+ 1 3+ 2
即y2 my .
3+4 3+12=0 ②
{ {
m m m
由 得y 4 代入 得 m2 m2 m2 2 解得 = 3, 或 =- 3,
①② 3=
1-
m2, ① ,4 +4(1- )-(1- ) =0,
y
3=-2 3
y
3=2 3
.
分
………………………………………………………………………………………… 9
{
m
当 = 3, 时 直线AB的方程为x y M MF
, = 3 +1, (3,-2 3),| |=4,
y
3=-2 3
y y y y .
1+ 2=4 3, 1 2=-4
所以 AB m2 y y y y 2 y y
| |= 1+ | 1- 2|=2 ( 1+ 2) -4 1 2 =2 48+16=16,
所以S 1 AB MF 1 .
△ MAB= ×| |×| |= ×16×4=32
2 2
{
m
当 =- 3,时 直线AB的方程为x y M MF
, =- 3 +1, (3,2 3),| |=4,
y
3=2 3
y y y y .
1+ 2=-4 3, 1 2=-4
所以 AB m2 y y y y 2 y y
| |= 1+ 1- 2 =2 ( 1+ 2) -4 1 2 =2 48+16=16,
所以S 1 AB MF 1 .
△ MAB= ×| |×| |= ×16×4=32
2 2
综上 MAB的面积为32. 分
,△ …………………………………………………………… 12
21. 思路导引 对a分类讨论
( )不等式同解变形 函数 φ(x) af(x) g(x) 求导
2 → = - → →
φ(x)的单调性 参数a的取值范围
→
【押题型】导数的几何意义 导数与函数的单调性 由不等式恒成立求参数的取值范围
, ,
【解】 因为g x x x 所以g g′ x x x x x x 则g′
(1) ( )=( -1)e +1, (1)= 1, ( )=e +( -1)e = e , (1)=
故函数g x 的图像在点M g 处的切线方程为y x 即ex-y-e+1=0.
e, ( ) (1, (1)) -1=e( -1),
分
………………………………………………………………………………………… 4
由题设 不等式ax x x x 对 x 恒成立 即不等式ax x
(2) , (e -1)≥( -1)e +1 ∀ ∈(-∞,0] , (e -
x x 对 x 恒成立.
1)+(1- )e -1≥0 ∀ ∈(-∞,0]
令φ x ax x x x x 则φ φ′ x a x x a x x.
( )= (e -1)+(1- )e -1, ∈(-∞,0], (0)=0, ( )= ( +1)e - - e
(导函数的正负不易判断,对导函数进行求导)
令h x φ′ x 则h′ x a x x x a x a x. 分
( )= ( ), ( )=[ ( +2)-( +1)]e =[( -1) +2 -1]e …………… 7
若a 则φ′ x x 当且仅当x 时 等号成立 故φ x 在 上单调递
① =1, ( )=e -1≤0, =0 , , ( ) (-∞,0]
减 所以φ x φ 满足题意. 分
, ( )≥ (0)=0, ………………………………………………… 8a
若a 令h′ x 得x 1-2 .
② ≠1, ( 0)=0, 0= a
-1
{a
当a 时
-1>0,
所以当x x 时 h′ x 则h x φ′ x 单调递减
1) >1 ,
x
∈(-∞, 0) , ( )<0, ( )= ( ) ;
0<0,
当x x 时 h′ x 则h x φ′ x 单调递增.
∈( 0,0] , ( )>0, ( )= ( )
所以在区间 x 上 φ′ x φ′ 所以 φ x 单调递减 则 φ x φ x
( 0,0] , ( )≤ (0)= 0, ( ) , ( 0)> ( )≥
φ .
(0)=0
在区间 x 上 当x 时 x φ′ x a 且 φ′ x 所以 φ x 单调递
(-∞, 0) , →-∞ ,e →0, ( )→- , ( 0)<0, ( )
减 则φ x φ x .所以在区间 上 有φ x 满足题意.
, ( )> ( 0)>0 (-∞,0] , ( )≥0,
当 1 a 时 x 所以当x 时 h′ x 故h x φ′ x 单调递增
2) ≤ <1 , 0≥0, ∈(-∞,0] , ( )≥0, ( )= ( ) ,
2
所以φ′ x φ′ 所以φ x 单调递减 则φ x φ 满足题意.
( )≤ (0)=0, ( ) , ( )≥ (0)=0,
{a
当a 1 时
-1<0,
所以当 x x 时 h′ x h x φ′ x 单调递增 当
3) <
2
,
x
∈(-∞, 0) , ( )>0, ( )= ( ) ;
0<0,
x x 时 h′ x h x φ′ x 单调递减.此时在区间 x 上 φ′ x φ′
∈( 0,0] , ( )<0, ( )= ( ) ( 0,0] , ( )≥ (0)=
所以φ x 单调递增 则φ x φ 不满足题意.
0, ( ) , ( )≤ (0)=0,
[ 1 )
综上 实数a的取值范围为 ,+∞ . 分
, 2 ……………………………………………… 12
22.【押题型】参数方程与普通方程 极坐标方程与直角坐标方程间的互化 参数的应用
、 ,
ì
ï
x 2t
ïï =1+ ,
【解】 由直线l的参数方程í 2 消去参数得 x y
(1) ï , - =2,
ïy 2t
î =-1+ ,
2
故直线l的普通方程为x-y-2=0. 分
…………………………………………………… 2
由ρ 6 θ θ得ρ2 ρ θ ρ θ .
+ ρ =6cos +2sin -6 cos -2 sin +6=0
又x ρ θ y ρ θ x2 y2 ρ2 所以x2 y2 x y
= cos , = sin , + = , + -6 -2 +6=0,
所以曲线C的直角坐标方程为x2+y2-6x-2y+6=0. 分
………………………………… 5
ì
ï
x 2t
ïï =1+ ,
将直线l的参数方程í 2 t为参数 代入方程x2 y2 x y
(2) ï ( ) + -6 -2 +6=0,
ïy 2t
î =-1+
2
整理得t2 t Δ . 分
-4 2 +4=0, =16>0 ……………………………………………………… 7
由题知点Q在直线l上 设点A B对应的参数分别为t t
, , 1,2,
则 QA t QB t 则t t t t 即t t 为正数
| |=| 1|,| |=| 2|, 1+ 2=4 2>0,1 2=4>0, 1,2 ,
故 ( 1 1 ) 2 ( 1 1 ) 2 ( 1 1 ) 2 ( t 1+ t 2) 2 -4 t 1 t 2 (4 2) 2 -16 1.
QA - QB = t - t = t - t = t t 2 = =
| | | | | 1| | 2| 1 2 ( 1 2) 16
分
………………………………………………………………………………………… 10
23.【押题型】绝对值不等式的解法 绝对值三角不等式 由不等式恒成立求参数的取值范围
, ,
【解】 当m 时 f x x x .
(1) =-4 ,( )=2| +1|+2| -2|-2
当x 时 f x x x x 解 x 得x
>2 ,( )=2 +2+2 -4-2=4 -4, 4 -4≥8 ≥3;
当 x 时 f x x x 不等式无解
-1≤ ≤2 ,( )=2 +2+4-2 -2=4<8, ;当x 时 f x x x x 解 x 得x . 分
<-1 ,( )=-2 -2+4-2 -2=-4 , -4 ≥8 ≤-2 ……………………… 4
综上 不等式f x 的解集为{x|x -2或x 3}. 分
, ( )≥8 ≤ ≥ ………………………………… 5
对 x R x R 使不等式f x g x 成立 即f x g x . 分
(2) ∀ 1∈ ,∃ 2∈ , ( 1)≥ ( 2) , ( )min≥ ( )min ……… 6
因为g x x 2 所以g x .
( )=( -2) , ( )min=0
因为f x x x m x x m x x m m
( )=2| +1|+|2 + |-2=|2 +2|+|2 + |-2≥|2 +2-(2 + )|-2=| -2|-2,
当且仅当 x x m 时 等号成立 所以f x m . 分
(2 +2)(2 + )≤0 , , ( )min=| -2|-2 ……………… 9
所以 m 解得m 或m
| -2|-2≥0, ≤0 ≥4,
故实数m的取值范围为(-∞,0] [4,+∞). 分
∪ ……………………………………… 102024 年全国高考名校名师联席命制
数学(文)押题卷(四)
题号 1 2 3 4 5 6 7 8 9 10
答案 B A C D D C B D D B
题号 11 12 13 14 15 16
答案 C D 1 1 答案不唯一
2 2 - ( )
2 2
1.B 【押考点】集合的并集运算 集合元素的特征
,
【深度解析】因为A B 所以 a a 所以a Z.解
∪ ={1,2,3,4,5,6}, { +2,2 +1}⊆{2,3,4,5,6}, ∈
a a 得a 解a a 得a 解a a 得a
提示:需分
+2≤6,2 +1≤6 ≤2; +2≥2,2 +1≥2 ≥1; +2≠2 +1 ≠1(
情况讨论
a
的值
所以
a
.
故选
B.
), =2
2.A 【押考点】复数的四则运算及模
【深度解析】z 2 2 2 提示:平方差
=(2+i) -(1+2i) =(3+3i)(1-i)=3(1+i)(1-i)=3(1-i )=6(
公式 所以 z 2 2 .故选A.
), | +8i|=|6+8i|= 6 +8 =10
一题多解 z ( )2 ( )2 ( 2) ( 2) ,所以 z
= 2+i - 1+2i = 4+4i+i - 1+4i+4i = 6 | +8i| =|6+8i| =
2 2 .故选 .
6 +8 =10 A
3.C 【押考点】向量数量积的坐标运算及夹角
【深度解析】因为b c x b c 易错:向量的数量积公式易混淆 即 x
=(2,1), =(1, ), · =4( ), 2+ =
b c
解得x 所以c 所以 b c · 4 4 .故选C.
4, =2, =(1,2), cos〈 , 〉= b c = =
| || | 5× 5 5
4.D 【押题型】三视图与体积计算
【深度解析】由三视图知 该几何体是底面直径为 高为 的圆柱 上接一个
, 2, 2 ,
底面直径为 2, 高为 3 的圆锥构成的组合体 , 如图.V 圆锥= 1 ×π×1 2 × 3= 3 π,
3 3
( )
V 圆柱=π×1 2 ×2=2π, 故几何体的体积为V 圆柱+ V 圆锥= 2+ 3 π .故选D.
3
5.D 【押考点】等差数列的定义 等差中项
,
【深度解析】因为a a 所以数列 a 是公差为 的等差数列 则原式 a
n +1- n=-2, { n} -2 , =5( 5+
a 提示:等差中项 .故选D.
6)=5×(18+16)=170( )
6.C【押考点】古典概型
【深度解析】不超过 的素数有 共 个 随机选取两个不同的
25 2,3,5,7,11,13,17,19,23, 9 ,
数有
(2,3),(2,5),(2,7),(2,11),(2,13),(2,17),(2,19),(2,23),(3,5),(3,7),(3,
11),(3,13),(3,17),(3,19),(3,23),(5,7),(5,11),(5,13),(5,17),(5,19),(5,23),
(7,11),(7,13),(7,17),(7,19),(7,23),(11,13),(11,17),(11,19),(11,23),(13,
共 种 其中和等于 的有
17),(13,19),(13,23),(17,19),(17,23),(19,23), 36 , 20 (3,
和 这 种情况 所以在不超过 的素数中 随机选取两个不同的数 其和等于
17) (7,13) 2 , 25 , ,
的概率是 2 1 .故选C.
20 =
36 18
7.B 【押考点】三角恒等变换
( ) ( )
【深度解析】由 2π θ π 得 π θ π π 又 θ π 3 所以 θ π
- ≤ ≤ , - ≤ + ≤ , sin + = , cos + =
3 3 2 6 2 6 3 6
( ) ( ) ( ) ( )
6 故 θ π θ π π θ π π θ π π 3 3 6
, sin + =sin + + =sin + cos +cos + sin = × + ×
3 3 6 6 6 6 6 6 3 2 3
1 3+ 6.故选B.
=
2 68.D 【押题型】利用导数研究函数的极值
x2 x x x
【深度解析】函数f x 的定义域为 f′ x 2 3 -3 +2 ( -1)( -2).
( ) (0,+∞), ( )= 1+ x2 - x = x2 = x2
当x 时 f′ x 当x 时 f′ x 当x 或x 时 f′ x
∈(0,1)∪(2,+∞) , ( )>0; ∈(1,2) , ( )<0; =1 =2 , ( )=
( )
x x . f x f x x x 1 1 x x .故
0,∴ 1=2, 2=1 ∴ ( 1)+ ( 2)= 1+ 2-2 x + x -3ln( 1 2)= 3-3-3ln 2=-3ln 2
1 2
选D.
9.D 【押考点】直线与双曲线的位置关系
【深度解析】由双曲线的对称性 不妨设点M的纵坐标y 如图.
, M≥0,
x2 x2
依题意 F .设P x y 则x 所以 PR x 3 .由 0 y2 得y2 0 所
, (2,0) ( 0, 0), 0≥ 3, | |= 0- - 0=1 0= -1,
2 3 3
PR
以 PF x 2 y2 x2 x y2 4 x2 x 2 3x 所以| | 3.故
| |= ( 0-2) + 0 = 0-4 0+4+ 0 = 0-4 0+3= 0- 3, PF =
3 3 | | 2
选D.
10.B 【押题型】根据分段函数的单调性求参数取值范围
【深度解析】因为函数y ax a a 是减函数 所以a .又因为函数y x2 a
=1- ( >0, ≠1) , >1 = +( -
a ( a)
x 图像的对称轴是直线x 5- 所以函数y x2 a x 在 5- 上单调递
5) +1 = , = +( -5) +1 -∞,
2 2
( a ) a
减 在 5- 上单调递增.又函数f x 是R上的减函数 所以a 5- 且a a
, ,+∞ ( ) , >1, ≥1, -3≥1- ,
2 2
解得 a 所以a的取值范围是 .故选B.
2≤ ≤3, [2,3]
11.C 【押素材】函数模型的应用 指对互化
、
TR TR
【深度解析】由题意 , W ( T R)=10 -6W 0, 即 e -τ =10 -6 , 等号两边同时取自然对数得 ln e -τ =
T
ln 10 -6 , 即 - τ R =-6ln 10, 所以T R= τ ×6ln 10= τ ×6×(ln 2+ln 5)≈13 . 8 τ.故选C.
12.D
思路导引 正四棱锥P ABCD与其外接球球O的位置关系 用球O的半径R表示正
- →
POE
四棱锥P ABCD的高和底面边长 用R表示正四棱锥P ABCD的体积 R Rt△
- → - → →
OE 点E的轨迹 点E的轨迹长度
→ →
【押考点】正四棱锥与球 动点轨迹
,
【深度解析】由题意 正四棱锥P ABCD内接于球O 且PO为四棱锥
, - ,
的高.设球O的半径为 R 如图所示 连接 AC BD 交于点 O 连接
, , , ,
PO
,
则AO
=
BO
=
PO
=
R.易得AB
= 2
R
,
所以V
四棱锥P - ABCD=
1
·
AB2
·
3
PO 1 R2 R 4 2 解得R .在 POE中 因为 EPO
= ·2 · = , = 2 Rt△ , ∠ =
3 3
π PO 所以OE PO EPO 6. 因为点 O 到正方形 ABCD 四边的距离为
, = 2, = ·tan∠ =
6 31 AB 6 所以点E的轨迹为底面ABCD内以O为圆心 半径r 6的圆.故点E的轨
=1> , , =
2 3 3
迹长度为 r 2 6π.故选D.
2π =
3
13. 【押考点】线性规划
2
【深度解析】根据约束条件作出可行域 如图中阴影部分 含边
, (
界 所示.作出直线 x y 并平移 由图可知 当直线过点 A
) + =0 , ,
{x y
时 z x y取得最大值 解 +2 -2=0,得x y 所以z x
, = + , x y =2, =0, = +
- -2=0,
y的最大值为 .
2
14. 【押考点】圆锥中的线面角
2
【深度解析】设该圆锥的底面圆半径和母线长分别为r l 母线与底面所成角为θ 由题意
,, ,
可得 rl r2 l r 易错:圆锥的侧面积公式 由勾股定理可得圆锥的高 h
π = 5π ⇒ = 5 ( ), =
h
r2 r2 r 所以圆锥的母线与底面所成角的正切值 θ .
5 - =2 , tan = r =2
15. 1 【押考点】直线与椭圆的位置关系
-
2
y
【深度解析】设点P x y 由题意可得A a A a 则k 0 1 k
( 0, 0), 1(- ,0), 2( ,0), PA
1
=x
0+
a=
3
①, PO=
ì
ïx 1 a
y ï 0= , y
0 联立 解得í 5 所以k 0 1 .
x 0 =2②, ①②, ï ïy 2 a PA 2 =x 0- a=- 2
î 0= ,
5
16. 1 答案不唯一
( )
2
思路导引 M→A·M→B 点M在以AB为直径的圆(记为圆C)上 点M在直线kx
=0→ → -
y k 上 直线与圆C有公共点 k的取值范围 k的值
+8 -2=0 → → →
【押题型】直线与圆的位置关系
【深度解析】因为 M→A M→B 所以点 M 在以 AB 为直径的圆 C 上.因为 A
· =0, (-6,-2),
AB
B 所以圆心C 半径r | | 所以圆C的方程为 x 2 y 2
(4,-2), (-1,-2), = =5, ( +1) +( +2) =
2
.因为点M在直线kx y k 上 所以直线与圆C相交或相切 即圆心C
25 - +8 -2=0 , , (-1,-2)
k k
到直线kx y k 的距离|- +2+8 -2| 化简得k2 25 解得 5 6 k 5 6
- +8 -2=0 ≤5, ≤ , - ≤ ≤ ,
1+
k2
24 12 12
( )
故k的一个可能取值为 1 答案不唯一 满足 5 6 k 5 6即可 .
, - ≤ ≤
2 12 12
17.【押素材】样本的数字特征
【解】因为甲研究员试验耗材量的极差为 且最小值为 所以n .
21, 15, =6
因为乙研究员试验耗材量的第 百分位数为 . 且 %
70 28 5, 10×70 =7,
m
所以20+ +30 . 即m . 分
=28 5, =7 ………………………………………………………… 3
2
甲研究员试验耗材量的平均数为
x 1
1= ×(15+18+20+24+25+25+26+29+32+36)=25,
10
乙研究员试验耗材量的平均数为
x 1 分
2= ×(15+20+20+23+25+25+27+30+30+35)=25, ……………………………… 7
10甲研究员试验耗材量的方差为
s2 1 2 2 2 2 2 2 2 2 .
1= ×[(-10) +(-7) +(-5) +(-1) +1 +4 +7 +11 ]=36 2,
10
乙研究员试验耗材量的方差为
s2 1 2 2 2 2 2 2 2 2 .
2= ×[(-10) +(-5) +(-5) +(-2) +2 +5 +5 +10 ]=30 8,
10
所以x x s2 s2 分
1= 2, 2< 1,……………………………………………………………………… 11
所以乙研究员试验耗材量的方差小于甲研究员试验耗材量的方差 说明乙研究员试验耗
,
材量相对于甲研究员试验耗材量更稳定. 分
…………………………………………… 12
18.【押题型】面面垂直的证明 点到平面的距离 棱锥的体积
, ,
【证明】在等腰梯形 ABCD 中 因为 AB CD AD 所以 ADC BCD °
(1) , =2 =2 =2, ∠ =∠ =120 ,
DAB ABC ° 所以 CAB ° 所以 ACB ° AC BC. 分
∠ =∠ =60 , ∠ =30 , ∠ =90 , ⊥ ………………… 2
因为平面PAB 平面ABCD 平面PAB 平面ABCD AB PA AB PA 平面PAB
⊥ , ∩ = , ⊥ , ⊂ ,
所以PA 平面ABCD.又BC 平面ABCD 所以PA BC. 分
⊥ ⊂ , ⊥ …………………………… 4
又PA AC A PA AC 平面PAC 所以BC 平面PAC.
∩ = , , ⊂ , ⊥
又BC 平面PBC 所以平面PAC 平面PBC. 分
⊂ , ⊥ ……………………………………… 6
【解】如图 过点A作AE PC于点E 由 可知平面PAC 平
(2) , ⊥ , (1) ⊥
面PBC
,
又平面PAC 平面 PBC PC AE 平面 PAC 所以 AE 平面
∩ = , ⊂ , ⊥
PBC 故AE 3. 分
, = ……………………………………………… 8
2
在 ADC中 ADC ° AD DC 所以AC .
△ ,∠ =120 , = =1, = 3
在 ACE中 AE 3 AC 所以 ACE °.
Rt△ , = , = 3, ∠ =30
2
PA
又PA AC ACP 3 所以PA 即四棱锥P ABCD的高为 . 分
⊥ ,tan∠ =AC= , =1, - 1 ……… 10
3
由题意知 梯形ABCD的高为 3 所以梯形ABCD的面积为 1 3 3 3
, , ×(1+2)× = ,
2 2 2 4
3
所以四棱锥P ABCD的体积为 1 3 3 . 分
- × ×1= 4 …………………………………… 12
3 4
19.【押考点】利用正余弦定理解三角形及基本不等式的应用
a b a b c2
【解】由a ( - )( + )+ 化简得a2 b2 c2 ab
(1) = a b , + - = ,
2 -
所以由余弦定理得 C
a2
+
b2
-
c2
1 . 分
cos = ab = ……………………………………………… 3
2 2
π
又因为 C 所以C . 分
0< <π, = 3 …………………………………………………………… 5
【证明】由 得a2 b2 c2 ab 由正弦定理得 2A 2B 3 A B 分
(2) (1) + - = , sin +sin - =sin sin , …… 7
4
由基本不等式得 A B 1 2A 2B 当且仅当 A B时 等号成立
sin sin ≤ (sin +sin ), sin =sin , ,
2
分
……………………………………………………………………………………… 9
所以 2A 2B 3 1 2A 2B
sin +sin - ≤ (sin +sin ),
4 2
当且仅当 A B 即 ABC为等边三角形时 等号成立 分
sin =sin , △ , , ……………………… 10
3
解得 2A 2B 3 所以 2A 2B的最大值为 . 分
sin +sin ≤ , sin +sin 2 …………………………… 12
220.【押题型】利用导数研究函数的单调性 零点个数 不等式的证明
、 ,
【解】由题可得 函数f x 的定义域为 .
(1) , ( ) (0,+∞)
由f x 得m 2 x. 分
( )=0 = x +ln ……………………………………………………………… 2
x
令g x 2 x x 则g′ x 2 1 -2.
( )= x +ln , >0, ( )=- x2 + x = x2
令g′ x 解得 x 令g′ x 解得x
( )<0, 0< <2, ( )>0, >2,
g x 在 上单调递减 在 上单调递增. 分
∴ ( ) (0,2) , (2,+∞) ……………………………… 4
当x 时 g x 取得极小值 也是最小值 最小值为g .
∴ =2 , ( ) , , (2)=1+ln2
作出g x 的大致图像 如图.
( ) ,
由图可知 当m 时 直线y m与函数 g x 的图像无交
, <1+ln 2 , = ( )
点 函数f x 的零点个数为 当m 时 直线y m与函
,∴ ( ) 0; =1+ln 2 , =
数g x 的图像有 个交点 函数f x 的零点个数为 当m
( ) 1 ,∴ ( ) 1; >1+ln2
时 直线y m与函数g x 的图像有 个交点 函数f x 的零点个
, = ( ) 2 ,∴ ( )
数为 . 分
2 …………………………………………………………………………………… 6
【证明】设f x 的两个零点分别为x x
(2) ( ) 1, 2,
由 知m 不妨令x x 则x x 且 2 x 2 x m.
(1) >1+ln2, 1< 2, 1<2< 2, x +ln 1=x +ln 2=
1 2
要证明两个零点之和大于 即x x 只需证x x
4, 1+ 2>4, 2>4- 1,
又x x 只需证g x g x 即g x g x . 分
2>2,4- 1>2, ( 2)> (4- 1), ( 1)- (4- 1)>0 …………………… 8
令F x g x g x x
( )= ( )- (4- ), ∈(0,2],
x x é ù
则F′ x -2 2- x êê 1 1 úú 在 上恒成立 分
( )= x2 + x 2 =(2- )·ë x 2 - x2 û<0 (0,2) , ………… 10
(4- ) (4- )
F x 在 上单调递减 当x 时 F x F
∴ ( ) (0,2) ,∴ ∈(0,2) , ( )> (2)=0,
g x g x 成立 x x 得证. 分
∴ ( 1)> (4- 1) ,∴ 1+ 2>4, …………………………………………… 12
21. 思路导引 ( )点A( t2, t) AB 2 导数与函数的最值 AB 的最小值;
1 4 4 →| | → →| |
和差角公式
( ) ACB 与 ACO, OCB 的关系 OCB, ACO ACB
2 ∠ ∠ ∠ →tan∠ tan∠ →tan∠ →
ACB的取值范围;
tan∠
( ) ACB与 ACO的范围 ACB与 ACO的大小关系 ACB与 ACO的
3 ∠ ∠ →tan∠ tan∠ →∠ ∠
大小关系
【押考点】与抛物线有关的弦长与角
【解】设A t2 t t 则 AB 2 t2 2 t 2 t4 t2 t .
(1) (4 ,4),≠0, | | =(4 +1) +(4 -4) =16 +24 -32 +17
设f t t4 t2 t t R 则f′ t t3 t t t2 t .
( )=16 +24 -32 +17,∈ , ( )=16(4 +3 -2)=16(2 -1)(2 + +2)
( ) ( )
2
因为 t2 t t 1 15 所以令f′ t 得t 1 f t 在 1 上单调递
2 + +2=2 + + >0, ( )= 0 = , ( ) -∞,
4 8 2 2
( )
减 在 1 上单调递增
, ,+∞ ,
2
( )
所以f t 的最小值为f 1 故 AB 的最小值为2 2. 分
( ) =8, | | …………………………… 4
2
t ( ]
【解】由题可知 OCB 4 ACO | | 1 提示:点A可能在x轴上
(2) tan∠ = ,tan∠ =t2 ∈ 0, (
3 +1 2
方,也可能在x轴下方,所以要分类讨论
.
)
25
ACO
当t 时 ACB OCB ACO 所以 ACB 4-3tan∠ 3 4 .
>0 ,∠ =∠ -∠ , tan∠ = ACO=- + ACO
3+4tan∠ 4 3+4tan∠( ]
因为 ACO 1 所以 1 ACB 4 分
tan∠ ∈ 0, , ≤tan∠ < ; ………………………………… 6
2 2 3
25
ACO
当t 时 ACB OCB ACO 所以 ACB 4+3tan∠ 3 4 .
<0 ,∠ =∠ +∠ , tan∠ = ACO=- + ACO
3-4tan∠ 4 3-4tan∠
( ]
因为 ACO 1 所以 4 ACB 11. 分
tan∠ ∈ 0, , 0 , ≥2;
当 1 x 时 f x x x x 解f x 得 3 x 分
- ≤ <2 ,( )=2 +1+2 -4=4 -3, ( )>0, < <2; ………………… 2
2 4
当x 1 时 f x f x 不成立 则x . 分
<- ,( )=-5,( )>0 , ∈⌀ …………………………………… 4
2
( 3 )
综上 不等式f x 的解集为 ,+∞ . 分
, ( )>0 4 …………………………………………… 5
令g x f x x 则g x x x x x 分
(2) ( )= ( )+4| -2|, ( )= |2 +1|+|2 -4|≥|2 +1-(2 -4)|=5, …… 7
当且仅当 x x 即 1 x 时等号成立 所以g x 的值域为 .
(2 +1)(2 -4)≤0, - ≤ ≤2 , ( ) [5,+∞)
2
由题意原不等式转化为 m2 m 恒成立 即 m2 m 分
2 -3 <5 , 2 -3 -5<0, ……………………… 9
( 5 )
解得 m 5 即实数m的取值范围为 -1, . 分
-1< < , 2 ………………………………… 10
22024 年全国高考名校名师联席命制
数学(文)押题卷(五)
题号 1 2 3 4 5 6 7 8 9 10
答案 C A B D D A D A D C
题号 11 12 13 14 15 16
答案 D D 3 38
9 55 (-2,- 3] ±
38
1.C 【押考点】集合的交集运算及对数不等式的解法
【深度解析】因为 A x x x x B 所以 A B
={ |log2 ≤1}={ |0< ≤2}, ={-1,0,1,2,3}, ∩ ={1,
.故选C.
2}
2.A 【押考点】复数的四则运算及模
2
【深度解析】由 2 2 及 2z 得 z 2+i 2i+i 1 所以 z
(1+i) =1+2i+i =2i (1+i) =2+i = = 2 = -i, | | =
2i 2i 2
1 5.故选A.
+1=
4 2
一题多解
因为( )2z ,所以z 2+i 2+i ,所以 z |2+i|
1+i =2+i =(
1+i
)2 =(
1+i
)(
1+i
) | | =
|1+i||1+i|
=
5 5.故选 .
= A
2× 2 2
3.B 【押考点】等比数列的通项公式 前n项和公式
、
【深度解析】设等比数列
{
a
n}
的公比为q
(
q
≠0)
.
∵
a
5=27
a
2,
即a
2
q3
=27
a
2,∴
q
=3
.
∵
S
3=
6
a q q2 a S 2(1-3 ) 6 .故选B.
26,∴ 1(1+ + )=26,∴ 1=2,∴ 6= =3 -1=728
1-3
一题多解 设等比数列{a
n
}的公比为 q(q
≠0
).
∵
a
5=27
a
2
,即 a
2
q3
=27
a
2
,解得 q
=
, S ,S S ,S S 是公比为 的等比数列. S , S S S S
3 ∴ 3 6- 3 9- 6 27 ∵ 3=26 ∴ 6= 6- 3+ 3=26×27+26=
.故选 .
728 B
4.D 【押考点】几何体的三视图和体积
【深度解析】根据几何体的三视图可得该几何体为上底面边长为 下底面边长为 高为
2, 4, 3
的正四棱台 故该几何体的体积V 1 .故选D.
, = ×3×(4+ 4×16+16)=28
3
5.D 【押素材】线性回归方程的应用
【深度解析】因为x 1 y 1 所以回归直
= ×(20+25+30+35+40)=30, = ×(5+7+8+9+11)=8,
5 5
线过点 故 . a^ 解得 a^ . 所以 y^ . x . . 将 x 代入 y^
(30,8), 8=0 25×30+ , =0 5, =0 25 +0 5 =45 =
. x . 得y^ . . . .故选D.
0 25 +0 5, =0 25×45+0 5=11 75
6.A 【押题型】利用函数的奇偶性 单调性解不等式
、
( ) x ( ) x
|-| | |
【深度解析】由题意可知f x 的定义域为R 且f x 1 1 f x
( ) , (- )= = = ( ),
2 2
( )x
所以f x 为偶函数.当x 时 函数f x 1 f x 单调递减.
( ) >0 , ( )= , ( )
2
若f a f a 成立 则 a a 解得a 或a 1 .
(2 )<( -1) , |2 |>| -1|, <-1 >
3
( )
又a 所以正实数a的取值范围是 1 .故选A.
>0, ,+∞
37.D 【押考点】直线与椭圆的位置关系 三角形的面积
,
x2 y2
【深度解析】如图 不妨设点A在x轴上方.在椭圆C
, : + =1
9 5
中 F F a . 由 AF 及椭圆定义得
,| 1 2| =2 9-5 =4,2 =6 | 2 | =4
AF 因此 AF F 为等腰三角形 底边上的高 h
| 1|= 2, △ 1 2 , =
( )
2
AF 2 1 AF 2 2 所以 AF F 的面
| 2| - | 1| = 4 -1 = 15, △ 1 2
2
积S 1 AF h .故选D.
△ AF 1 F 2 = 2 | 1|· = 15
8.A 【押题型】圆的方程 直线与圆的位置关系 点到直线的距离公式
, ,
y
【深度解析】由题可得 圆C的圆心为C 半径为 的几何
, (-2,5), 2, x
意义为圆C上的点 P x y 与坐标原点 O 连线的斜率 如
( , ) (0,0) ,
图.过原点O作圆C的切线 当切线的斜率存在时 设切线方程为
, ,
y kx 即kx y 所以圆心C 到直线 kx y 的距离 d
= , - =0, (-2,5) - =0 =
k y
|2 +5| 解得k 21.故由图可知 的最大值是 21 故选A.
=2, =- x - ,
k2
+1 20 20
9.D 【押考点】平面向量的坐标运算与夹角
【深度解析】 a b k a b k 解得k b .
∵ =(1,-1), =(2, ), ⊥ ,∴2- =0, =2,∴ =(2,2)
c a tb c t t c 0.
∵ = - ,∴ =(1-2,-1-2), ≠
a c b c a c b c
∵ 〈 , 〉=〈 , 〉,∴ cos〈 , 〉=cos〈 , 〉,
a c b c
即 · · t 解得t 1 .故选D.
a c = b c ,∴2=-4, =-
| || | | || | 2
10.C 【押考点】异面直线所成角
【深度解析】如图 连接AC 与BD交于点O 则O为AC的中点 取PC
, , , ,
的中点E 连接OE DE 则OE AP EOD为异面直线AP与BD所
, , , ∥ ,∴ ∠
成的角或其补角.
PD 平面ABCD CD 平面ABCD PD CD.
∵ ⊥ , ⊂ ,∴ ⊥
PC DE 5.又OE 1 PA 5 OD 1 BD
∵ = 5,∴ = = = , = = 2,
2 2 2 2
5 5
OD2 OE2 DE2 2+ -
在 ODE中 根据余弦定理可得 EOD + - 4 4 10.故选C.
△ , cos∠ = OD OE = =
2 · 5 5
2× 2×
2
11.D
思路导引 函数f(x)有两个零点 函数g(x) x x的图像与直线y a有两个交
→ =e - =2-
点 对函数g(x)求导 判断单调性,求得最值 a的取值范围
→ → →
【押考点】函数的零点问题 利用导数研究函数的单调性及参数的取值范围
,
【深度解析】设g x x x 则函数f x 有两个零点转化为函数g x x x的图像与直
( )=e - , ( ) ( )=e -
线y a有两个交点.因为g′ x x 当x 时 g′ x 当x 时 g′ x 所
=2- ( )=e -1, <0 , ( )<0; >0 , ( )>0,
以g x 在区间 上单调递减 在区间 上单调递增 则g x g 0
( ) (-∞,0) , (0,+∞) , ( )≥ (0)=e -
当x 时 g x 当x 时 g x 则 a 解得a 即实数a
0=1, →-∞ , ( )→+∞; →+∞ , ( )→+∞, 2- >1, <1,
的取值范围是 .故选D.
(-∞,1)一题多解 函数f(x) x x a 有两个零点可转化为函数h(x) x 的图像与直线
=e - + -2 =e
y x a有两个交点.因为函数h(x)的图像与y轴交于点( , ),直线y x a与y轴
= +2- 0 1 = +2-
交于点( , a),所以点( , a)在点( , )上方,即 a ,解得a ,即实数a的取值
0 2- 0 2- 0 1 2- >1 <1
范围是( , ).故选 .
-∞ 1 D
12.D
思路导引 思路一:令 x y f( ) 令 y x 函数 f(x) 的奇偶性
= = 0→ 0 → = - → →
当x 时,f(x)
<0 <0 函数f(x)的单调性 f(x)在区间[ , ]上的最大值 关于m的一元
f(x)的奇偶性→ → -2 2 →
二次不等式 实数m的取值范围
→
当x 时,f(x)
思路二:令y <0 <0 x y x,f(x y) f(x) 函数f(x)的单调性 f(x)在区
<0 → + < + < → →
间[ , ]上的最大值 关于m的一元二次不等式 实数m的取值范围
-2 2 → →
【押风向】抽象函数的单调性 图像的对称性 不等式有解问题
、 ,
【深度解析】令x y 得 f f f f 所以 f 令 y x 则有
=0, =0, (0)= (0)+ (0)= 2 (0), (0)= 0; =- ,
f f x f x 即f x f x 则f x f x 故f x 是定义在R上的奇函
(0)= ( )+(- ), ( )+ (- )= 0, (- )= - ( ), ( )
数.设x x 则x x 又当x 时 f x 则有f x x 即f x x f x
1< 2, 1- 2<0, <0 , ( )<0, ( 1- 2)<0, ( 1- 2)= ( 1)+
f x f x f x 则 f x f x 故f x 在 上单调递增. 所以当
(- 2)= ( 1)- ( 2)<0, ( 1)< ( 2), ( ) (-∞,+∞)
x 时 f x f . 又因为存在 x 使得 f x m2 m 成立 所
∈[-2,2] ,( )≤ (2)= 3 ∈[-2,2], ( )> -2 ,
以m2 m 解得 m .故选D.
-2 -3<0, -1< <3
快解 令y ,则x y x.因为f(x y) f(x) f(y),当x 时,f(x) ,所以f(x y)
<0 + < + = + <0 <0 + <
f(x),即函数f(x)在R上单调递增.因为存在x [ , ],使得f(x) m2 m成立,所以
∈ -2 2 > -2
m2 m f(x) ,f(x) 为 f(x)在区间[ , ]上的最大值.因为 f(x)在 R 上单调递
-2 < max max -2 2
增,f( ) ,所以 f(x) ,所以m2 m . 解得 m ,即实数 m 的取值范围为
2 =3 max=3 -2 <3 -1< <3
( , ).故选 .
-1 3 D
13. 【押风向】等差数列的性质 对数的运算
9 ,
【深度解析】 数列 a 的首项a 且数列 a 是以 为公差的等差数列
∵ { n} 1=1, {log2 n} 1 ,
a a n n a a .
∴ log2 1=0,log2 n=0+( -1)×1= -1,∴ log2 3+log2 8=(3-1)+(8-1)=9
14. 【押考点】循环结构的程序框图
55
【深度解析】初始值i S 第一次循环 S 2 i 不满足退出循环条件 继
=1, =0, , =0+1 =1, =1<5, ,
续循环
;
第二次循环 i S 2 i 不满足退出循环条件 继续循环
, =2, =1+2 =5, =2<5, , ;
第三次循环 i S 2 i 不满足退出循环条件 继续循环
, =3, =5+3 =14, =3<5, , ;
第四次循环 i S 2 i 不满足退出循环条件 继续循环
, =4, =14+4 =30, =4<5, , ;
第五次循环 i S 2 i 满足退出循环条件 输出S .
, =5, =30+5 =55, =5, , =55
15. 【押题型】三角函数的图像变换 正弦型函数的图像与性质
(-2,- 3] ,
【深度解析】根据f x 的部分图像 可得A .
( ) , =1
( ) ( ) ( )
由题图可知点 2 10 1 在 f x 的图像上 则 ω 2 φ
,1 , ,- ( ) , sin × + = 1,
3 3 2 3
( )
ω 10 φ 1 根据五点作图法可得ω 2 φ π ω 10 φ π 解得ω
sin × + =- , × + = , × + =2π- , =
3 2 3 2 3 6( )
π φ π 则f x πx π .将函数 f x 图像上所有点的横坐标缩短为原来的
, = , ( )=sin + ( )
2 6 2 6
( )
π 纵坐标伸长到原来的 倍得到y x π 的图像 再把得到的图像向左平移π
, 2 =2sin 2 + ,
4 6 12
( )
个单位长度 可得到g x x π 的图像.
, ( )=2sin 2 +
3
作出函数g x 的部分图像如图所示
( ) ,
根据函数g x 的图像知 当 m 时 直线y m与
( ) , -2< ≤- 3 , =
[ ]
函数 g x 在 π 上的图像有两个交点 即方
( ) - ,0 ,
2
[ ]
程g x m在 π 上有两个不相等的实数根.
( )= - ,0
2
16. 3 38
±
38
思路导引 联立
直线l的方程,双曲线C的方程 点A,B坐标间的关系, PQ 点A,B
→ | |→
解方程
到直线l的距离 S S k的值
→ 1 2 →
【押考点】双曲线的方程和性质 直线与双曲线的位置关系
、
x2
【深度解析】由题意 得双曲线C的方程为 y2 A B 直线l的方程为
, - =1, (-2,0), (2,0),
4
y kx .
= -1
{x2
y2
由
4
- =1,消去y整理得
(1-4
k2
)
x2
+8
kx
-8=0,
y kx
= -1,
则Δ k2 解得k2 1 .
=32(1-2 )>0, <
2
k
设P x y Q x y 则x x -8 x x -8
( 1, 1), ( 2, 2), 1+ 2= k2, 1 2= k2,
1-4 1-4
由直线l与双曲线C的左 右两支相交可得x x -8
、 1 2= k2<0,
1-4
所以 k2 解得k2 1
1-4 >0, < ,
4
k2 k2
所以 PQ k2 x x k2 x x 2 x x 4 2 1+ 1-2 .
| |= 1+ | 1- 2|= 1+ ( 1+ 2) -4 1 2 = k2
1-4
k
又点A 到直线l y kx 的距离d |-2 -1|
(-2,0) : = -1 1= k2 ,
+1
k
点B 到直线l y kx 的距离d |2 -1|
(2,0) : = -1 2= k2 ,
+1
k2
所以d d 1-4 .
1 2= k2
+1
k2
所以S S 1 PQ d 1 PQ d 8(1-2 )
1 2= | | 1· | | 2= k2 =80,
2 2 1-4
所以k2 9 满足k2 1 解得k 3 38.
= , < , =±
38 4 38
17.【押题型】利用正弦 余弦定理解三角形及三角形面积公式
、
A A
【解】 因为a B b 2 所以由正弦定理可得 B A B 2 .
(1) sin =2 3 sin , sin sin =2 3sin sin
2 2A ( ) A
因为 A B 所以 B π
0< <π,0< <π, sin >0, ∈ 0, ,sin >0,
2 2 2
A A A A A π
所以 2 所以 3 所以 π A . 分
2sin cos =2 3sin , tan = , = , = 3 …………… 5
2 2 2 2 3 2 6
根据已知条件有a A 3 A 1 ABC的面积为9 3
(2) =2 6,sin = ,cos = ,△ ,
2 2 4
所以 1 bc A 3bc 9 3 即bc
sin = = , =9,
2 4 4
所以由余弦定理a2 b2 c2 bc A得 b2 c2 bc 所以b2 c2 . 分
= + -2 cos 24= + - , + =33 ……………… 6
如图 取BC的中点D 连接AD.
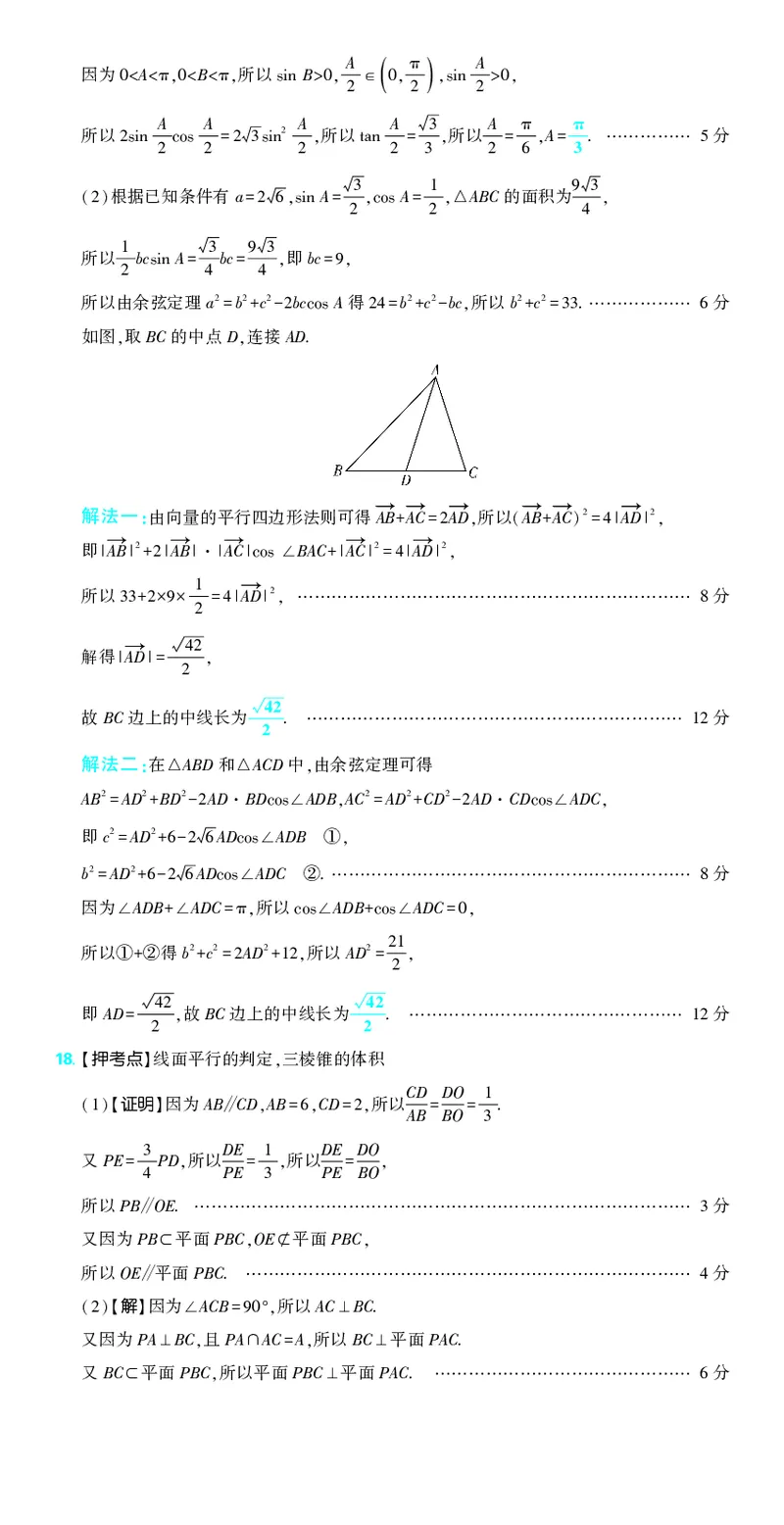
, ,
解法一:由向量的平行四边形法则可得→AB →AC A→D 所以 →AB →AC 2 A→D 2
+ =2 , ( + ) =4| | ,
即 →AB 2 →AB →AC BAC →AC 2 A→D 2
| | +2| |·| |cos ∠ +| | =4| | ,
所以 1 A→D 2 分
33+2×9× =4| | , …………………………………………………………… 8
2
解得 A→D 42
| |= ,
2
42
故BC边上的中线长为 . 分
2 ………………………………………………………… 12
解法二:在 ABD和 ACD中 由余弦定理可得
△ △ ,
AB2 AD2 BD2 AD BD ADB AC2 AD2 CD2 AD CD ADC
= + -2 · cos∠ , = + -2 · cos∠ ,
即c2 AD2 AD ADB
= +6-2 6 cos∠ ①,
b2 AD2 AD ADC . 分
= +6-2 6 cos∠ ② ……………………………………………………… 8
因为 ADB ADC 所以 ADB ADC
∠ +∠ =π, cos∠ +cos∠ =0,
所以 得b2 c2 AD2 所以AD2 21
①+② + =2 +12, = ,
2
42
即AD 42 故BC边上的中线长为 . 分
= , 2 ………………………………………… 12
2
18.【押考点】线面平行的判定 三棱锥的体积
,
CD DO
【证明】因为AB CD AB CD 所以 1 .
(1) ∥ , =6, =2, AB=BO=
3
DE DE DO
又PE 3 PD 所以 1 所以
= , PE= , PE=BO,
4 3
所以PB OE. 分
∥ …………………………………………………………………………… 3
又因为PB 平面PBC OE 平面PBC
⊂ , ⊄ ,
所以OE 平面PBC. 分
∥ …………………………………………………………………… 4
【解】因为 ACB ° 所以AC BC.
(2) ∠ =90 , ⊥
又因为PA BC 且PA AC A 所以BC 平面PAC.
⊥ , ∩ = , ⊥
又BC 平面PBC 所以平面PBC 平面PAC. 分
⊂ , ⊥ ……………………………………… 6如图 作AH PC 垂足为H.因为平面PBC 平面PAC PC AH
, ⊥ , ∩ = , ⊂
平面PAC 所以AH 平面PBC.
, ⊥
在 PAC中 PA AC PC 所以AH .
△ , =2 3, =2 3, =4, =2 2
又BF 2 AB 所以点F到平面PBC的距离d 4 2. 分
= , = ……… 10
3 3
在 ABC中 AC AB 所以BC .
Rt△ , =2 3, =6, =2 6
又BC 平面PAC PC 平面PAC 所以BC PC.
⊥ , ⊂ , ⊥
又PC 所以S 1PC BC
=4, △ PBC= · =4 6,
2
32 3
所以V 1 S d 1 4 2 . 分
三棱锥F - PBC= △ PBC· = ×4 6× = 9 ……………………………… 12
3 3 3
一题多解 ( )因为 ACB °,所以AC BC.
2 ∠ =90 ⊥
又因为PA BC,PA AC A,所以BC 平面PAC.
⊥ ∩ = ⊥
又因为BC 平面ABC,所以平面ABC 平面PAC. ………… 分
⊂ ⊥ 6
在 PAC中,作PG AC于G,因为平面ABC 平面PAC AC,
△ ⊥ ∩ =
所以PG 平面ABC.
⊥
在 PAC中,PA ,AC ,PC ,所以PG 4 6. …… 分
△ =2 3 =2 3 =4 = 8
3
因为AF 1 AB CD且AF CD,所以四边形ADCF为平行四边形,
= = ∥
3
所以AD CF,所以 CFB °.
∥ ∠ =90
在 ACD中,由勾股定理得AD CF,
△ =2 2=
又BF 2 AB ,所以S 1 CF·BF .
= =4 △ CFB= =4 2
3 2
所以V V 1 S ·PG 32 3. …………………………………… 分
三棱锥F - PBC= 三棱锥P - CFB= △ CFB = 12
3 9
19.【押素材】频率分布直方图 中位数及古典概型的应用
、
【解】 由频率分布直方图 得 . . . a . .
(1) , 10×(0 004+0 008+0 012+ +0 026+0 032)=1,
解得a 0.018. 分
= …………………………………………………………………………… 3
由频率分布直方图 得 . . . . .
(2) , 10×(0 004+0 008+0 012)=0 24<0 5,
. . . . .
10×(0 004+0 008+0 012+0 026)=0 5,
则估计这 名学生成绩的中位数为80. 分
600 …………………………………………… 4
由题意得 成绩在 的频率为 . . 成绩在 的频率为
(3) , [40,60) 0 012×10=0 12, [90,100]
. . 频率之比为
0 018×10=0 18, 2 ∶ 3,
所以按分层抽样的方法从中选取 人 成绩在 的学生有 人 分别记为a a 成
5 , [40,60) 2 , 1, 2,
绩在 的学生有 人 分别记为b b b . 分
[90,100] 3 , 1, 2, 3 …………………………………… 7
从这 人中任意选取 人 有a a a b a b a b a b a b a b b b b b b b 共
5 2 , 1 2, 1 1, 1 2, 1 3, 2 1, 2 2, 2 3, 1 2, 1 3, 2 3, 10
种选法 分
, ………………………………………………………………………………… 10
其中至少有 人成绩不低于 分的选法有 a b a b a b a b a b a b b b b b
1 90 1 1, 1 2, 1 3, 2 1, 2 2, 2 3, 1 2, 1 3,
b b 共 种
2 3, 9 ,
9
所以这 人中至少有 人成绩不低于 分的概率P . 分
2 1 90 =10 ………………………… 12
20. 思路导引 联立抛物线方程
( )直线l 的方程 设出直线l 的方程 化简求出P,Q两点坐
2 1 → 2 →
标关系 联立直线PB与直线l 的方程求出x 同理可得x x x x AM AN
→ 1 M→ N→ M+ N=2 A→| |=| |【押题型】抛物线的定义 标准方程及直线与抛物线的综合问题
、
p
【解】因为抛物线C y2 px上一点 y 到其准线x 的距离为
(1) : =2 (2, 0) =- 3,
2
p
所以 解得p 分
+2=3, =2, ……………………………………………………………… 3
2
所以抛物线C的标准方程为y2=4x. 分
…………………………………………………… 4
【证明】直线l x y 令x 得y 所以点B .
(2) :2 - +4=0, =0 =4, (0,4)
因为直线l 平行于直线l 且过点A
1 , (2,1),
所以直线l x y . 分
1:2 - -3=0 ……………………………………… 6
由题知直线l 的斜率不为 所以设直线l x t y t .
2 0, 2: -2= ( -1),≠2
{x t y
由 -2= ( -1),消去x得y2 ty t
-4 +4 -8=0,
y2 x
=4 ,
则Δ t2 t .
=16( - +2)>0
设P x y Q x y 则y y t y y t .
( 1, 1), ( 2, 2), 1+ 2=4, 1 2=4 -8
y y
直线PB的方程为y 1-4x 直线QB的方程为y 2-4x . 分
= x +4, = x +4 …………………… 8
1 2
ì y
ï ïy 1-4x x ty t
解í = x +4,得x 7 1 7( 1+2-)
î
ïï
x y
1 M=
2
x
1-
y
1+4
=
(2
t
-1)
y
1+8-2
t,
2 - -3=0,
ty t
同理可得x 7( 2+2-) 分
N= t y t, ………………………………………………………… 9
(2 -1) 2+8-2
ty t ty t
所以x x 7( 1+2-) 7( 2+2-)
M+ N= t y t+ t y t
(2 -1) 1+8-2 (2 -1) 2+8-2
t t y y t t t t y y t t
2(2 -1) 1 2+[(8-2) +(2 -1)(2-)]( 1+ 2)+2(2-)(8-2)
= t 2y y t t y y t 2 ×7
(2 -1) 1 2+(2 -1)(8-2)( 1+ 2)+(8-2)
t2 t
4 -4 +8 . 分
= t2 t =4 ………………………………………………………………………… 10
- +2
因为x 所以x x x 即A是线段MN的中点 所以 AM AN . 分
A=2, M+ N=2 A, , | |=| | ………… 12
21. 思路导引 ( )对f(x)求导 判断f′(x)的正负 f(x)的单调性;
1 → →
( )将原不等式转化为 x [ , ), x x2 ax x 恒成立 构造函数F(x)
2 ∀ ∈ 0 +∞ e - -2 -cos ≥0 → =
x x2 ax x,x [ , ) 对F′(x)求导 对a分类讨论 F′(x)的正负 F(x)
e - -2 -cos ∈ 0 +∞ → → → →
的单调性 a的取值范围
→
【押考点】利用导数判断函数单调性 根据不等式恒成立求参数取值范围
,
【解】 当a 时 f x x x2 所以f′ x x x
(1) =1 ,( )=e - +2, ( )=e -2 ,
令m x x x 所以m′ x x
( )=e -2 , ( )=e -2,
当x 时 m′ x
ln2 , ( )>0,
所以m x m 即f′ x
( )≥ (ln2)=2-2ln2>0, ( )>0,
从而函数f(x)在(-∞,+∞)上单调递增. 分
…………………………………………… 5
因为f x x ax2 所以f′ x x ax
(2) ( )=e - +2, ( )=e -2 ,
又g x x2 x
( )= +cos ,
x f′ x g x 恒成立等价于 x x x2 ax x 恒成立.
∀ ∈[0,+∞), ( )≥ ( ) ∀ ∈[0,+∞),e - -2 -cos ≥0
分
……………………………………………………………………………………… 7
记F x x x2 ax x x 所以F′ x x x a x.
( )=e - -2 -cos , ∈[0,+∞), ( )=e -2 -2 +sin令h x x x a x x 所以h′ x x x .
( )=e -2 -2 +sin , ∈[0,+∞), ( )=e +cos -2
设r x x x x 从而r′ x x x
( )=e +cos -2, ∈[0,+∞), ( )=e -sin >0,
则r x 在 上单调递增
( ) [0,+∞) ,
故有r x r 则h x 在 上单调递增
( )≥ (0)=0, ( ) [0,+∞) ,
即F′ x 在 上单调递增 故有F′ x F′ a. 分
( ) [0,+∞) , ( )≥ (0)=1-2 ……………………… 8
当a 1 时 F′ x F′ a 此时F x 单调递增
≤ , ( )≥ (0)=1-2 ≥0, ( ) ,
2
从而F x F 满足题意.
( )≥ (0)=0,
当a 1 时 F′ a 且F′ x 在 上单调递增
> , (0)=1-2 <0, ( ) (0,+∞) ,
2
故存在x 满足F′ x
0∈(0,+∞) ( )=0,
则F x 在 x 上单调递减 所以当x x 时 F x F 不满足题意.
( ) (0, 0) , ∈[0, 0) , ( )≤ (0)=0,
( 1 ]
综上 a的取值范围为 -∞, . 分
, 2 …………………………………………………… 12
22.【押题型】参数方程与普通方程 直角坐标方程与极坐标方程的互化
、
{x α
【解】 因为曲线C 的参数方程为 =2+2cos , α为参数 消去参数可得曲线C 的
(1) 1 y α ( ), 1
=2sin
普通方程为(x-2)2+y2=4. 分
……………………………………………………………… 2
由题可知曲线C 的直角坐标方程为y x 即x y .
2 = -1, - -1=0
将x ρ θ y ρ θ代入
= cos , = sin ,
得ρ θ ρ θ
cos - sin -1=0,
( π) 2
则曲线C 的极坐标方程为ρcos θ+ = . 分
2 4 2 ……………………………………… 4
曲线C 的极坐标方程为θ π ρ R 则曲线C 的直角坐标方程为x
(2) 3 = ( ∈ ), 3 =0,
2
则C 与C 的交点M C 与C 的交点N 分
3 1 (0,0), 3 2 (0,-1), …………………………… 8
所以 MN 1. 分
| |= ………………………………………………………………………… 10
一题多解 ( )由( )可知C 的普通方程为(x )2 y2 ,即x2 y2 x,故极坐标方
2 1 1 -2 + =4 + =4
程为ρ θ. ………………………………………………………………………… 分
=4cos 6
{ρ θ,
=4cos
曲线C 的极坐标方程为θ π(ρ R),由 解得ρ ;
3 = ∈ θ π, M=0
2 =
2
ì ( )
ï
ρ θ π 2,
ï cos + =
由í 4 2 解得ρ ,
ï
N=-1
ïθ π,
î =
2
所以 MN ρ ρ . ……………………………………………………………… 分
| |=| M- N|=1 10
23.【押题型】绝对值三角不等式的性质 基本不等式的应用
,
【解】 x R f x m恒成立
(1)∵ ∀ ∈ ,( )≥ ,
m x x 在x R上恒成立
∴ ≤| -2|+| +2| ∈ ,
m x x . 分
∴ ≤(| -2|+| +2|)min ……………………………………………………………… 2
又 x x x x 当且仅当 x x 即 x
∵ | -2|+| +2|≥|( -2)-( +2)| =4, ( -2)( +2)≤0, ∈[-2,2]
时 等号成立
, ,
m 即实数m的取值范围为(-∞,4]. 分
∴ ≤4, …………………………………………… 4由 可知函数f x 的最小值k b a 1 a a.
(2) (1) ( ) =4,∴ ( -1)= ×4+2 =2+2
2
a
a b a b 2 +2. 分
∵ >0, >0,∴ >1, = a …………………………………………………………… 7
-1
a
a b a 2 +2 a 4 a 4
∴ + = + a = -1+a +3≥2 ( -1)·a +3=7,
-1 -1 -1
当且仅当a 4 即a 时 等号成立
-1=a , =3 , ,
-1
a b的最小值为7. 分
∴ + …………………………………………………………………… 102024 年全国高考名校名师联席命制
数学(文)押题卷(六)
题号 1 2 3 4 5 6 7 8 9 10
答案 B B C A A B A D C D
题号 11 12 13 14 15 16
[ )
答案 B C 1 2 2022
-8 ,+∞ -1
2 5
1.B 【押考点】集合的并集运算
【深度解析】 A x x B x x A B x x .故选B.
∵ ={ |0< <1}, ={ |-1< <2},∴ ∪ ={ |-1< <2}
2.B 【押考点】复数的运算 共轭复数
、
【深度解析】由题知 复数z 2+i z .故选B.
, = =1-2i,∴ =1+2i
i
3.C 【押考点】中位数 众数 平均数 极差的概念
、 、 、
【深度解析】由题意 数据从小到大排列为 这组数据的
, 95,96,96,96,97,97,98,98,99,100,
中位数是 1 故A正确 在这组数据中 出现的次数最多 故众数是 故
×(97+97)=97, ; 96 , 96,
2
B正确 这组数据的平均数是 1 . 故C不
; ×(95+96+96+96+97+97+98+98+99+100)=97 2,
10
正确 这组数据的极差是 故D正确.故选C.
; 100-95=5,
4.A 【押风向】空间线面的位置关系 充分条件与必要条件的判断
、
【深度解析】因为m n是两条相交直线 α β是两个互相平行的平面 且n β m α 则可设
, , , , ∥ , ∥ ,
直线m n所在平面为 γ 则 α β γ 故 m β 即充分性成立 因为 m n 是两条相交直
, , ∥ ∥ , ∥ , ; ,
线 α β是两个互相平行的平面 且n β m β 则m α 或者m α 故必要性不成立.综
, , , ∥ , ∥ , ∥ , ⊂ ,
上 m α 是 m β 的充分不必要条件.故选A.
,“ ∥ ” “ ∥ ”
5.A 【押考点】双曲线的方程与性质
ì c
ï2 =4, ìa
ïïb ï ï =1, y2
【深度解析】由题意知í 解得íb 故双曲线 C 的标准方程为 x2 .故
ïa = 3, ï = 3, - =1
ï 3
ï îc
îa2 b2 c2 =2,
+ = ,
选A.
6.B 【押题型】程序框图 等比数列求和
、
【深度解析】该算法的功能是计算a 1 2 3 2 022 1-2
2023
2 023.故选B.
=2+2 +2 +2 +…+2 =1+ =2
1-2
7.A 【押考点】等差数列的前n项和的最值
【深度解析】因为a a 即a a 所以 a 为等差数列 且公差为 .又a
n +1= n-3, n +1- n=-3, { n} , -3 1=
所以a n 所以 a a a a a 所以 S 最大 且 S
20, n =23-3 , 1> 2>…> 7>0> 8> 9>…, 7 , 7 =7×20+
7×6 .故选A.
×(-3)=77
2
8.D 【押考点】直线与圆的位置关系
【深度解析】由题知 直线l x y 圆C x 2 y 2 m m 令 m r2.因
, : +2 -1=0, :( -1) +( -2) =5- ( <5), 5- =
为圆C被直线l所截得的弧长之比为 所以两段弧所对圆心角之比为 .设圆C与
1 ∶ 2, 1 ∶ 2
直线l的交点分别为A B 则劣弧所对的圆心角 ACB ° 又CA CB r 所以圆心C到
, , ∠ =120 , = = ,r
直线l的距离为|1+2×2-1| 故r 8 5 所以 m 64 解得m 39.故选D.
= , = , 5- = , =-
1 2 +2 2 2 5 5 5
9.C 【押考点】向量的线性运算与数量积运算
【深度解析】如图 在 ACD中 记→CA a C→D b 则A→D C→D →CA b a.
, △ , = , = , = - = -
B→D A→D 0 D→B A→D b a C→B C→D D→B b a. 又 a b a b
∵ +2 = ,∴ =2 =2 -2 , = + =3 -2 | | =3,| | = 2,〈 , 〉=
π C→B b2 a2 a b 2 .故选C.
,∴ | |= 9 +4 -12 · = 18+36-12×3× 2× =3 2
4 2
一题多解
在 ACD 中, →CA , C→D , ACD π, 由余弦定理得AD
∵ △ | | =3 | | = 2 ∠ = ∴ =
4
AC2 CD2 AC·CD· ACD . B→D A→D 0, A,D,B 三点共线,且 BD
+ -2 cos∠ = 5 ∵ +2 = ∴ =
AD , AB .在 ACD中,由余弦定理得 CAD 9+5-2 2 5.在 ABC
2 =2 5 ∴ =3 5 △ cos∠ = = △
2×3× 5 5
中,由余弦定理得BC2 2 5 , BC ,即 C→B ,故选 .
=9+45-2×3×3 5× =18 ∴ =3 2 | |=3 2 C
5
10.D 【押考点】正弦函数的图像与性质 三角函数图像的平移变换
、
( ) ( ) ( )
【深度解析】 函数f x 的图像关于点 π 中心对称 f π 2π φ 又
∵ ( ) ,0 ,∴ =2sin + =0,
3 3 3
( )
π φ π φ π 则f x x π .将函数f x 的图像向右平移π个单位长
- < < ,∴ = , ( )=2sin 2 + ( )
2 2 3 3 3
( )
度得到函数g x x π 的图像 提示:三角函数图像的左右平移遵循“左加右
( )=2sin 2 - (
3
k
减”的原则 .令 x π k k Z 得x π π k Z 函数g x 在区间 内的
) 2 - = π, ∈ , = + , ∈ ,∴ ( ) [-π,π]
3 6 2
零点有x 5π x π x π x 2π 共 个 故选D.
=- , =- , = , = , 4 ,
6 3 6 3
方法总结 已知函数f(x) (ωx φ)(ω ),若求函数f(x)的单调递增区间,则令
=sin + >0
π k ωx φ π k ,k Z;若求函数f(x)的单调递减区间,则令π k ωx
- +2 π≤ + ≤ +2 π ∈ +2 π≤ +
2 2 2
φ 3π k ,k Z;若求函数f(x)的极值点或图像的对称轴,则令ωx φ π k ,k Z;
≤ +2 π ∈ + = + π ∈
2 2
若求函数f(x)的零点或图像的对称中心,则令ωx φ k ,k Z.
+ = π ∈
11.B 【押风向】函数与数列的综合应用
【深度解析】易知函数f
(
x
)=
x5
+2
x3
+3
x是奇函数
,
且在R上单调递增.
∵
a
n +3 =
a
n(
n
∈
N∗
),∴
a
1=
a
2 023=1,
a
2=
a
2 024,
a
3=
a
2 025,∴
f
(
a
1)+
f
(
a
2+
a
3)=
f
(
a
2 023)+
f
(
a
2 024+
a
2 025)=
f a f a a f a a a a a 即a a a 数列 a 的前
0,∴ ( 1)=- ( 2+ 3)= (- 2- 3),∴ 1=- 2- 3, 1+ 2+ 3=0,∴ { n}
项和为 a a a a a .故选B.
2023 674×( 1+ 2+ 3)+ 2 023=0+ 1=1
12.C
思路导引 正四棱台的几何性质 勾股定理
已知条件 棱台的高 外接球的球心 M 外
→ → →
球的体积公式
接球的半径 解题
→【押考点】正四棱台的外接球
【深度解析】如图 令O O分别是正四棱台ABCD A B C D 的上 下底面的中心 连接
, 1, - 1 1 1 1 、 ,
OO A O OA 则上底面外接圆半径r A O 下底面外接圆半径r AO 则该
1, 1 1, , 1= 1 1= 2, = =2 2,
棱台的高为 2 2 .设外接球的半径为R 显然球心M在OO 所在的直线
( 3) -( 2) =1 , 1
上.如图 当棱台两底面在球心异侧时 即球心M在线段OO 上 设OM x x 则
①, , 1 , = ,0< <1,
O M x 由MA MA R 得 2 x2 2 x 2 解得x 5 舍去 则
1 =1- , = 1= , (2 2) + = ( 2) +(1- ) , =- <0, ;
2
棱台两底面在球心同侧 显然球心 M 在 O O 的延长线上 如图 . 设 OM x x 则
, 1 , ② = , >0,
O M x 由 MC MA R 得 2 x2 2 x 2 解得 x 5 R
1 =1+ , = 1 = , (2 2) + = ( 2) +(1+ ) , = ,∴ =
2
( ) 2 ( ) 3
2 5 57 该正四棱台的外接球的体积为4πR3 4π 57
(2 2) + = ,∴ = × =
2 2 3 3 2
19 57π.故选C.
2
图 图
① ②
13. 【押题型】简单的线性规划问题
-8
【深度解析】作出可行域如图中阴影部分 含边界 所示 作出直线 x y 并平移.由图
( ) , 5 -3 =0
知 当目标函数表示的直线经过点A 时 目标函数取得最小值 且z .
, (-1,1) , , min=-5-3=-8
[ )
14. 1 【押考点】利用导数研究函数的单调性 不等式恒成立求参数的取值范围
,+∞ 、
2
m
【深度解析】 f x x2 x m x在定义域内单调递增 f′ x x 在 上
∵ ( )= -2 + ln ,∴ ( )=2 -2+ x ≥0 (0,+∞)
( )
2
恒成立 即m x2 x在 上恒成立.令g x x2 x x 1 1 x
, ≥-2 +2 (0,+∞) ( )=-2 +2 =-2 - + ( >
2 2
( )
g x g 1 1 提示:二次函数的性质 m 1 即实数 m的取值范围
0),∴ ( )max= = ( ),∴ ≥ ,
2 2 2
[ )
为 1 .
,+∞
2
2022
15.2
5思路导引 等比数列的求和公式 等比数列的通项公式
已知条件 公比、首项 a
→ → 2 023
【押考点】等比数列的通项公式与求和公式
【深度解析】 设正项等比数列 a 的公比为 q 由题意知 q 且 q 则
{ n} , > 0 ≠1,
a q4
1(1- )
S q a q4
S
4
8
=a
1(
1
1
-
-
q8
)
=
1+
1
q4 =
1
1
7
,∴
q
=2,
则S
4=
1(
1
1
-
-
q
)
=15
a
1=3,∴
a
1=
5
1
,∴
a
2 023=
a
1
q2 022
=
q
1-
1 2 022 2
2022
.
×2 =
5 5
一题多解 设正项等比数列{a }的公比为q.根据等比数列的性质知S ,S S ,S S
n 4 8- 4 12- 8
S S
成公比为 q4 的等比数列,
∴
q4
=
8
S
- 4
=
51-3
=16
. 又
∵
等比数列{a
n
}的各项均为正
4 3
数,
∴
q
=2
.
∵
S
4=
a
1
(
1-
q
q4)
=15
a
1=3
,
∴
a
1=
1 ,
∴
a
2 023=
a
1
q2 022
=
1
×2
2 022
=
2 2 022 .
1- 5 5 5
16.
-1
思路导引 抛物线的定义
已知条件 p 抛物线 C 点 P 设 PA:y k (x )
→ → → → = 1 -1 +2
联立方程
点A 点B k
→ → → AB
【押考点】抛物线的方程与性质 直线与抛物线的位置关系
、
p p
【深度解析】抛物线C y2 px p 的准线方程为x PF 提示:抛
: =2 ( >0) =- ,∴ | |= +1=2(
2 2
物线上的点到焦点的距离等于其到准线的距离 解得 p 抛物线 C y2 x P
), =2,∴ : =4 , (1,
.设直线PA y k x 代入抛物线方程y2 x 消去y 并整理得k2x2 k k2
2) : = 1( -1)+2, =4 , 1 +(4 1-2 1-
k2 k k
4)
x
+(
k2
1-4
k
1+4)= 0
.
∵
P
(1,2),∴
x
A=
1-4
k2
1+4
,
代入 y
=
k
1(
x
-1)+2,
得 y
A=
4-
k
2 1
,
1 1
( )
k2 k k
A 1-4 1+4 4-2 1 .设直线 PB 的斜率为 k 直线 PA PB 关于直线 x 对称
∴ k2 , k 2,∵ , =1 ,
1 1
( )
k2 k k
k k 直线PB y k x 同理可得B 1+4 1+4 -4-2 1 则直线AB的
∴ 1+ 2=0,∴ : =- 1( -1)+2, k2 , k ,
1 1
y y
斜率k B- A .
AB=x x =-1
B- A
17.【押考点】解三角形 正弦定理和余弦定理的应用 三角形的面积公式 三角恒等变换
、 、 、
【解】 在 ABC中 A b C c B a
(1) ∵ △ ,5cos ( cos + cos )=3 ,
由正弦定理可得 A B C C B A
∴ 5cos (sin cos +sin cos )=3sin ,
即 A B C A A A.
5cos sin( + )=5cos sin =3sin
A A A 3 分
∵ ∈(0,π),sin >0,∴ cos = , …………………………………………………… 3
5
A 9 4
∴ sin = 1- = ,
25 5
ABC的面积为 1 bc A 1 4 2. 分
∴ △ sin = ×5× = ………………………………………… 6
2 2 5
【证明】由余弦定理得 A
b2
+
c2
-
a2
(
b
+
c
)
2
-2
bc
-
a2
(
b
+
c
)
2
-10-(2 5)
2
3
(2) cos = bc = bc = = ,
2 2 10 5b c . 分
∴ + =6 ………………………………………………………………………………… 8
{b {b
又 bc
=1,或 =5,
分
∵ =5,∴ c c . …………………………………………………………… 9
=5 =1
当a b c 时 C
a2
+
b2
-
c2
5 C为钝角 此时 ABC是钝角三角
=2 5, =1, =5 ,cos = ab =- <0,∴ , △
2 5
形 分
; ……………………………………………………………………………………… 10
当a b c 时 同理可得B为钝角 此时 ABC是钝角三角形. 分
=2 5, =5, =1 , , △ ………… 11
综上 ABC是钝角三角形. 分
,△ …………………………………………………………… 12
18.【押考点】线面垂直的判定定理 点到平面的距离
、
【证明】 在直四棱柱 ABCD A B C D 中 BB 底面 ABCD BC 底面 ABCD
(1) ∵ - 1 1 1 1 , 1⊥ , ⊂ ,
BB BC.
∴ 1⊥
又AB BC BB AB B BB AB 平面ABB A BC 平面ABB A . 分
⊥ , 1∩ = , 1, ⊂ 1 1,∴ ⊥ 1 1 …………… 2
AB 平面ABB A BC AB . 分
∵ 1⊂ 1 1,∴ ⊥ 1 …………………………………………………… 3
易知四边形ABB A 是正方形 A B AB
1 1 ,∴ 1 ⊥ 1,
又A B BC B AB 平面A BC. 分
1 ∩ = ,∴ 1⊥ 1 …………………………………………………… 5
( )
【解】V V 1 1 4 . 分
(2) 三棱锥A 1- BCD= 三棱锥B - A 1 CD= 3 × 2 ×2×2 ×2= 3 ………………………… 7
A D CD A C
∵ 1 = 5, = 5, 1 =2 3,
S 1 . 分
∴ △ A 1 CD= 2 ×2 3× 5-3= 6 ……………………………………………………… 9
设点B到平面A CD的距离为h
1 ,
1 S h 6h 4 解得h 2 6
∴ 3 × △ A 1 CD× = 3 = 3 , = 3 ,
2 6
点B到平面A CD的距离为 . 分
∴ 1 3 …………………………………………………… 12
19.【押素材】线性回归方程 古典概型
、
【解】 x . y 1
(1)∵ =5 5, = ×(2+8+9+12+10+13+15+16+17+18)=12,
10
∑i
10x
i
y
i=787,∑i
10x2i
=385,
=1 =1
10xy x y
∴ b ^=
∑i
=
∑i
1 10
i
x2i
i
-
-
1
1
0
0
x2 = 78 3 7 8 - 5- 10 1 × 0× 5
.
5 5 . × 5 2 12 ≈1 . 54, ………………………………………… 2 分
=1
a^ . . . 分
∴ =12-1 54×5 5=3 53,……………………………………………………………… 3
线性回归方程为y^ . x . . 分
∴ =1 54 +3 53 …………………………………………………… 4
当x 时 y^ . . .
=11 , =1 54×11+3 53=20 47,
在不改变经营状态的情况下 预测该小卖部 年的年利润为20.47万元. 分
∴ , 2023 …… 6
年的年利润中低于 万元的有 个 不低于 万元的有 个
(2)2013~2022 12 4 , 12 6 ,
按照分层抽样从 年的年利润中随机抽取 个 则年利润低于 万元的有
2013~2022 5 , 12 2
个 记为A B 不低于 万元的有 个 记为C D E.
, , , 12 3 , , ,
从这 个数据中随机抽取 个 所有等可能结果有 AB AC AD AE BC BD BE CD
5 2 , , , , , , , , ,
CE DE 共 种
, , 10 ,
其中 抽取的 个数据至少有 个低于 万元的结果有AB AC AD AE BC BD BE 共 种
, 2 1 12 , , , , , , , 7 ,分
………………………………………………………………………………………… 10
7
故所求概率为 . 分
10 ……………………………………………………………………… 12
20. 思路导引 联立方程
( )已知条件 a Δ b k y S b 椭圆Γ的
1 → → 1=0→ =2 3 → P→ △ PA 1 A 2 → →
标准方程;
直线的方程与性质 BE
( )联立方程 Δ ,x x ,x x BE , BF BE BF | |
2 → 2>0 1+ 2 1 2 →| | | |→| |-| |=0→ BF
| |
是定值
1
【押题型】椭圆的方程与性质 直线与椭圆的位置关系
、
【解】由题知B A A a 解得a
(1) (4,0),| 1 2|=2 =4, =2,
x2 y2
椭圆Γ b .
∴ : + b2 =1(0< <2)
4
ì
ïï
x2 y2
b
由í + b2 =1(0< <2),
4
ïï
îy kx k k
= -4 ( >0),
b2 k2 b2
消去x并整理得 +4 y2 8 y b2 b k
k2 + k +12 =0(0< <2, >0),
b4 b2 b2 k2 b2 b2 k2
Δ 64 48 ( +4 ) 16 ( -12 )
1= k2 - k2 = k2 =0,
b2 k2 即b k. 分
∴ =12 , =2 3 ………………………………………………………………… 3
b2
8
k
y 3b
∴ P=- b2 k2 =- ,
2( +4 ) 2
k2
PA A 的面积为 1 3b 解得b 分
∴ △ 1 2 ×4× =3, = 3,……………………………………… 5
2 2
x2 y2
椭圆Γ的标准方程为 + =1. 分
∴ 4 3 …………………………………………………… 6
{x2 y2
【证明】由 + =1,
4 3
(2)
y kx k k
= -4 ( >0),
消去y并整理得 k2 x2 k2x k2
(3+4 ) -32 +64 -12=0,
Δ k2 解得 k 1 .
2=144(1-4 )>0, 0< <
2
设C x y D x y
( 1, 1), ( 2, 2),
k2 k2
则x x 32 x x 64 -12. 分
1+ 2= k2, 1 2= k2 ……………………………………………………… 8
3+4 3+4
由k 得 x x y y .
>0, -2< 1, 2<2, 1<0, 2<0
A A
∵ 1(-2,0), 2(2,0),
y
直线A C的方程为y 1 x
∴ 1 =x ( +2),
1+2
y y y
令x 解得y 6 1 BE 6 1 6 1 .
=4, E=x ,∴ | |= x =-x
1+2 1+2 1+2
y
同理 直线A D的方程为y 2 x
, 2 =x ( -2),
2-2y y y
令x 解得y 2 2 BF 2 2 2 2 . 分
=4, F=x ,∴ | |= x =x …………………………………… 10
2-2 2-2 2-2
y y k x k x x x x x
BE BF 6 1 2 2 6 ( 1-4) 2 ( 2-4) k 4 1 2-10( 1+ 2)+16
∴ | |-| | =-x -x =- x - x =-2 · x x =
1+2 2-2 1+2 2-2 ( 1+2)( 2-2)
k2 k2
64 -12 320
4× k2 - k2 +16
k 3+4 3+4 则 BE BF
-2 · x x =0, | |=| |,
( 1+2)( 2-2)
BE
| |是定值1. 分
∴ BF ……………………………………………………………………… 12
| |
21. 思路导引 导数的几何意义
( )已知条件 f(x) f( ),f′(x) f′( ) 切线的方程
1 → → 1 → 1 →
求导
( )已知条件 f(x)的定义域 当a 时,设h(x) xf(x) h(x)
2 → → =1 = 零点存在定理→ ≤0→
不等式的性质
x x x x x ax x x 结论成立
ln + +1≤ e →ln + +1≤ e →
【押考点】导数的几何意义 利用导数研究函数的单调性与最值 不等式恒成立问题
、 、
x
【解】当a 时 f x x ln 1 x
(1) =e ,( )=-e + x + x +e( >0),
x x
f f′ x x 1-ln 1 x ln f′ 分
∴ (1)=1, ( )=-e + x2 - x2 =-e - x2 , (1)=-e, ………………………… 3
当a 时 曲线y f x 在点 f 处的切线方程为y x 即ex+y-1-e=0.
∴ =e , = ( ) (1,(1)) -1=-e( -1),
分
………………………………………………………………………………………… 4
x
【证明】由题知 函数f x x ln 1 a的定义域为
(2) , ( )=-e + x + x + (0,+∞),
当a 时 设h x xf x x x x x x
=1 , ( )= ( )=ln + - e +1, ∈(0,+∞),
( )
则h′ x 1 x x x 1 x .
( )= x +1-( +1)e =( +1) x -e
令t x 1 x x
( )= x -e , ∈(0,+∞),
则t′ x 1 x 对任意x 恒成立 t x 在 上单调递减
( )=- x2 -e <0 ∈(0,+∞) ,∴ ( ) (0,+∞) ,
( )
又t 1 t
=2- e>0,(1)=1-e<0,
2
( )
x 1 使得t x 即 1
x
0 则 x x . 分
∴ ∃ 0∈ ,1 , ( 0)=0, x =e , -ln 0= 0 …………………………… 7
2 0
当 x x 时 t x 则h′ x h x 单调递增
∴ 0< < 0 ,( )>0, ( )>0, ( ) ;
当x x 时 t x 则h′ x h x 单调递减
> 0 ,( )<0, ( )<0, ( ) ,
h x h x x x x
x
0
∴ ( )≤ ( 0)=ln 0+ 0- 0e +1=0-1+1=0,
即 x x x x. 分
ln + +1≤ e ……………………………………………………………………… 10
又 a x x ax x x x x
∵ ≤1, >0,∴ ln + +1≤ln + +1≤ e ,
x ax x x
∴ ln + +1≤ e ,
当a 时 xf x 在定义域内恒成立. 分
∴ ≤1 , ( )≤0 ………………………………………… 12
22.【押考点】参数方程与普通方程 极坐标方程与直角坐标方程间的相互转化 参数的几何
、 ,
意义ì
ï
x 2t
ïï = ,
【解】 直线l的参数方程为í 2 t为参数
(1)∵ ï ( ),
ïy 2t
î = -3
2
直线l的普通方程为x-y-3=0. 分
∴ …………………………………………………… 2
曲线C的极坐标方程为ρ2 ρ θ
∵ -4 cos -4=0,
且x ρ θ y ρ θ x2 y2 ρ2
= cos , = sin , + = ,
曲线C的直角坐标方程为(x-2)2+y2=8. 分
∴ ………………………………………… 5
易知点P 在直线l上 分
(2) (0,-3) , ……………………………………………………… 6
ì
ï
x 2t
ïï = ,
将í 2 代入 x 2 y2 整理得t2 t .
ï ( -2) + =8, -5 2 +5=0
ïy 2t
î = -3
2
设点E F对应的参数分别为t t 则t t t t 分
, 1,2, 1+ 2=5 2,1 2=5,…………………………… 8
PE PF t t t t 2 t t 2 30. 分
∴ || |-| ||=| 1- 2|= ( 1+ 2) -41 2 = (5 2) -4×5= …………… 10
一题多解 由题知点P在直线l上且在圆C外.
圆心C( , )到直线l:x y 的距离d |2-3| 2,
∵ 2 0 - -3=0 = =
1 2 +1 2 2
( )
2
PE PF EF ( )2 2 . ……………………………… 分
∴ || |-| ||=| |=2 2 2 - = 30 10
2
23.【押考点】绝对值不等式的解法 不等式恒成立求参数的取值范围
,
【解】 f x x x
(1)∵ ( )= | +1|+| -3|,
当x 时 f x x x x 解 x 得x
∴ ≤-1 ,( )=- -1- +3=-2 +2, -2 +2≥6, ≤-2;
当 x 时 f x x x 无解
-1< <3 ,( )= +1- +3=4,4≥6, ;
当x 时 f x x x x 解 x 得x .
≥3 ,( )= +1+ -3=2 -2, 2 -2≥6, ≥4
综上 不等式f x 的解集为(-∞,-2] [4,+∞). 分
, ( )≥6 ∪ ……………………………… 5
f x a2 a的解集为R f x a2 a.
(2)∵ ( )≥2 +2 ,∴ ( )min≥2 +2
ì x x
ï-2 +2, ≤-1,
ï
由 可得f x í x f x . 分
(1) ( )=ï4,-1< <3, ∴ ( )min=4 ……………………………………… 8
ï
î x x
2 -2, ≥3,
a2 a 解得 a 实数a的取值范围为[-2,1]. 分
∴2 +2 ≤4, -2≤ ≤1,∴ …………………… 10