文档内容
2024 届高考新结构数学-选择填空强化训练(8)
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有
一项是符合题目要求的.
1.某地有8个快递收件点,在某天接收到的快递个数分别为360,284,290,300,188,240,260,
288,则这组数据的百分位数为75的快递个数为( )
A. 290 B. 295 C. 300 D. 330
【答案】B
【解析】将数据从小到大排序为:188,240,260,284,288, 290,300,360,
,所以 分位数为 .
故选:B
2.若集合 , ,则 ( )
A. B. C. D.
【答案】D
【解析】因为 ,所以 定义域为 ,
所以 ,即 ,
所以 .
故选:D.
3.设函数 ,数列 , 满足 , ,则 ( )
A. B. C. D.
【答案】B
【解析】因为 ,所以 ,
又因为 ,所以 ,
令 ,解得 ,
故选:B.
4.抛物线 的焦点为F,且抛物线C与椭圆 在第一象限的交点为A,若
轴,则 ( )
A. 2 B. 1 C. D.
【答案】C
【解析】由题设 ,且 在第一象限, 轴,则 ,又 在椭圆上,故 ,而 ,故 .
故选:C
5.某单位计划从5人中选4人值班,每人值班一天,其中第一、二天各安排一人,第三天安排两人,
则安排方法数为( )
A. 30 B. 60 C. 120 D. 180
【答案】B
【解析】先从5人中选出4人值班,
再从4人中选出2人值第三天,剩余2人分别值第一、二天,
所以安排方法数为 .
故选:B.
6.已知 是 的重心, 是空间中的一点,满足 ,
,则 ( )
A. B. C. D.
【答案】C
【解析】由题意知 是 的重心,则 ,即
所以 ,
又因为 ,
所以 .
故选:C.
7.已知 , ,则
( )
A. B. C. D.
【答案】A
【解析】 ,
.,
, ,
, ,
又因为 ,所以 ,
则 ,所以
.
.
故选:A
8.已知O为坐标原点,双曲线C: 的左、右焦点分别是F,F,离心率为 ,
1 2
点 是C的右支上异于顶点的一点,过F作 的平分线的垂线,垂足是M, ,
2
若双曲线C上一点T满足 ,则点T到双曲线C的两条渐近线距离之和为( )
A. B. C. D.
【答案】A
【解析】
设半焦距为c,延长 交 于点N,由于PM是 的平分线, ,
所以 是等腰三角形,所以 ,且M是NF的中点.
2
根据双曲线的定义可知 ,即 ,由于 是 的中点,
所以MO是 的中位线,所以 ,又双曲线的离心率为 ,所以 , ,所以双曲线C的方程为 .
所以 , ,双曲线C的渐近线方程为 ,
设 ,T到两渐近线的距离之和为S,则 ,
由 ,即 ,
又T在 上,则 ,即 ,解得 , ,
由 ,故 ,即距离之和为 .
.
故选:A
二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合
题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.
9.下列命题正确的是( )
A. 若 两组成对数据的样本相关系数分别为 ,则 组数据比 组数据的相关
性较强
B. 若样本数据 的方差为2,则数据 的方差为8
C. 已知互不相同的30个样本数据,若去掉其中最大和最小的数据,剩下28个数据的22%分位数不等
于原样本数据的22%分位数
D. 某人解答5个问题,答对题数为 ,若 ,则
【答案】BCD
【解析】对于A,因为 ,即 组数据比 组数据的相关性较弱,故A错误;
对于B,若样本数据 方的差为 ,则数据 的方差为
,故B正确;
对于C,将这原来的30个数从小大大排列为 ,则 ,所以原来的22%分位
数为 ,
若去掉其中最大和最小的数据,剩下28个数据为 ,则 ,所以剩下28个数
据的22%分位数为 ,
由于 互不相同,所以C正确;
对于D,某人解答5个问题,答对题数为 ,若 ,则 ,故D正确.
故选:BCD.
10.设复数 的共轭复数为 , 为虚数单位,则下列命题正确的是( )
A.若 ,则 B.若 ,则
C.若 ,则 D.若 ,则 的最小值是
【答案】ABD【解析】设 ,
对于选项A: ,所以 ,所以 ,故选项A正确;
对于选项B: ,所以 ,即 ,故选项B正确;
对于选项C: ,则 ,故选项C不正确;
对于选项D: 即 表示点 到点
和到点 的距离相等,所以复数 对应的点的轨迹为线段 的垂直平分线,
因为 中点为 , ,
所以 的中垂线为 ,整理可得: ,
所以 表示点 到 的距离,
所以 ,故选项D正确,
故选:ABD.
11.设函数 的定义域为 ,若存在 ,使得 ,则称 是函数 的二阶不
动点.下列各函数中,有且仅有一个二阶不动点的函数是( )
A. B.
C. D.
【答案】ACD
【解析】若 ,称 为一阶不动点,
显然若 ,则满足 ,故一阶不动点显然也是二阶不动点,
若 ,则有 ,即 都在函数 的图象上,
即 上存在两点关于 对称,此时这两点的横坐标也为二阶不动点,
下证:当 单调递增时,一阶不动点和二阶不动点等价,
因为 ,若 ,因为 单调递增,所以 ,
即 ,矛盾,
若 ,因为 单调递增,所以 ,即 ,矛盾,
综上:当 单调递增时,一阶不动点和二阶不动点等价;由题意得:只需 与直线 的交点个数为1,
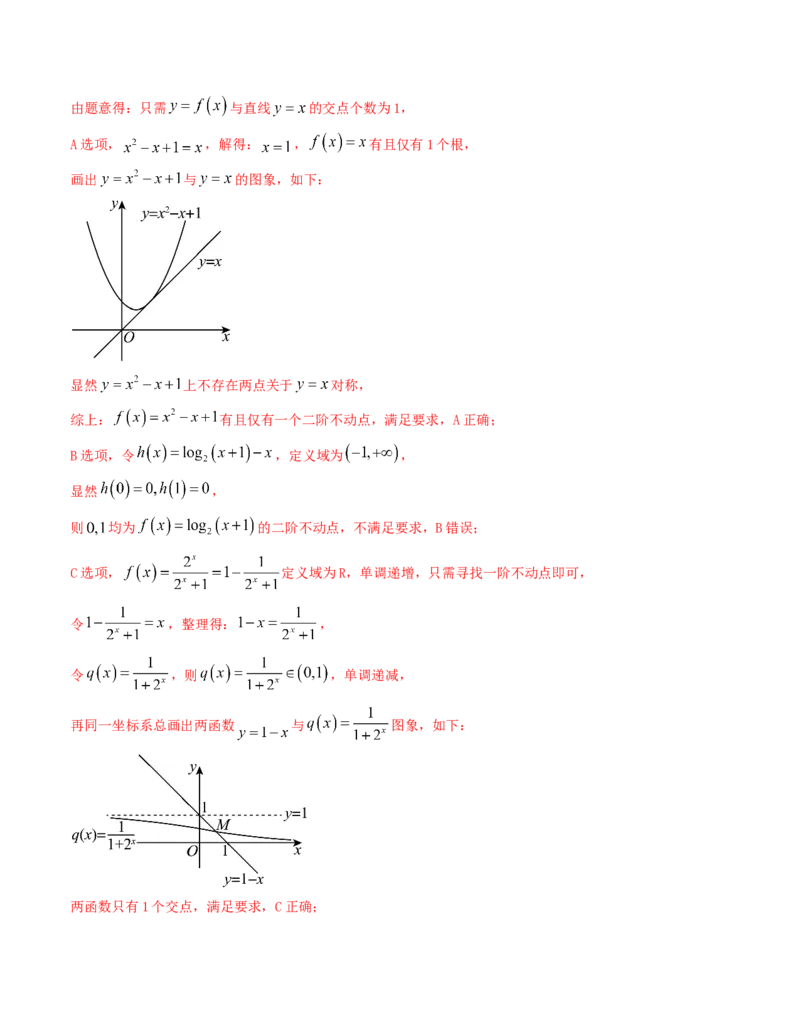
A选项, ,解得: , 有且仅有1个根,
画出 与 的图象,如下:
显然 上不存在两点关于 对称,
综上: 有且仅有一个二阶不动点,满足要求,A正确;
B选项,令 ,定义域为 ,
显然 ,
则 均为 的二阶不动点,不满足要求,B错误;
C选项, 定义域为R,单调递增,只需寻找一阶不动点即可,
令 ,整理得: ,
令 ,则 ,单调递减,
再同一坐标系总画出两函数 与 图象,如下:
两函数只有1个交点,满足要求,C正确;D选项,令 ,
作出函数 的图象,
由图可知,点 与点 关于直线 对称,
故函数满足题意,故D正确.
故选:ACD.
三、填空题:本题共3小题,每小题5分,共15分.
12.已知 的展开式中 的系数为240,则实数 ______.
【答案】
【解析】 ,
二项式 通项公式为 ,
的
其中 的展开式中无含 项,含 的项为 ,
∴ 中含 的项为 ,则 .解得 .
故答案为:
13.已知四面体 ,其中 , , , 为 的中
点,则直线 与 所成角的余弦值为__________;四面体 外接球的表面积为__________.
【答案】 ①. ## ②.
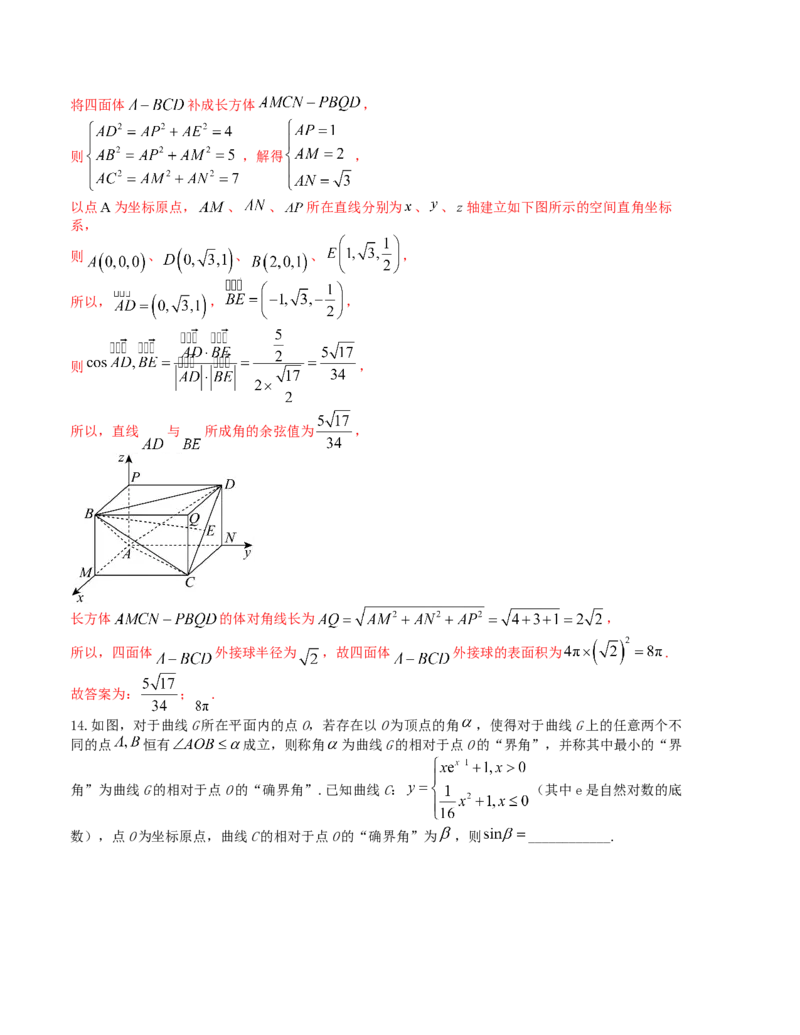
【解析】在四面体 中, , , ,将四面体 补成长方体 ,
则 ,解得 ,
以点 为坐标原点, 、 、 所在直线分别为 、 、 轴建立如下图所示的空间直角坐标
系,
则 、 、 、 ,
所以, , ,
则 ,
所以,直线 与 所成角的余弦值为 ,
长方体 的体对角线长为 ,
所以,四面体 外接球半径为 ,故四面体 外接球的表面积为 .
故答案为: ; .
14.如图,对于曲线G所在平面内的点O,若存在以O为顶点的角 ,使得对于曲线G上的任意两个不
同的点 恒有 成立,则称角 为曲线G的相对于点O的“界角”,并称其中最小的“界
角”为曲线G的相对于点O的“确界角”.已知曲线C: (其中e是自然对数的底
数),点O为坐标原点,曲线C的相对于点O的“确界角”为 ,则 ____________.【答案】1
【解析】函数 ,
因为 ,
所以该函数在 单调递减,在 单调递增.
过原点作 的切线,设切点 ,
由 ,则切线 的斜率为 ,
直线 过 ,
∴ ,∴ ,
即 ,由函数 与 的图象在 有且只有一个交点,
且当 时满足方程,故方程有唯一解 ,则 ;
过原点作 的切线,设切点 ,
由 ,得切线 的斜率 ,
则切线 过原点 ,
则有 ,∴ ,则 ,则有 ,
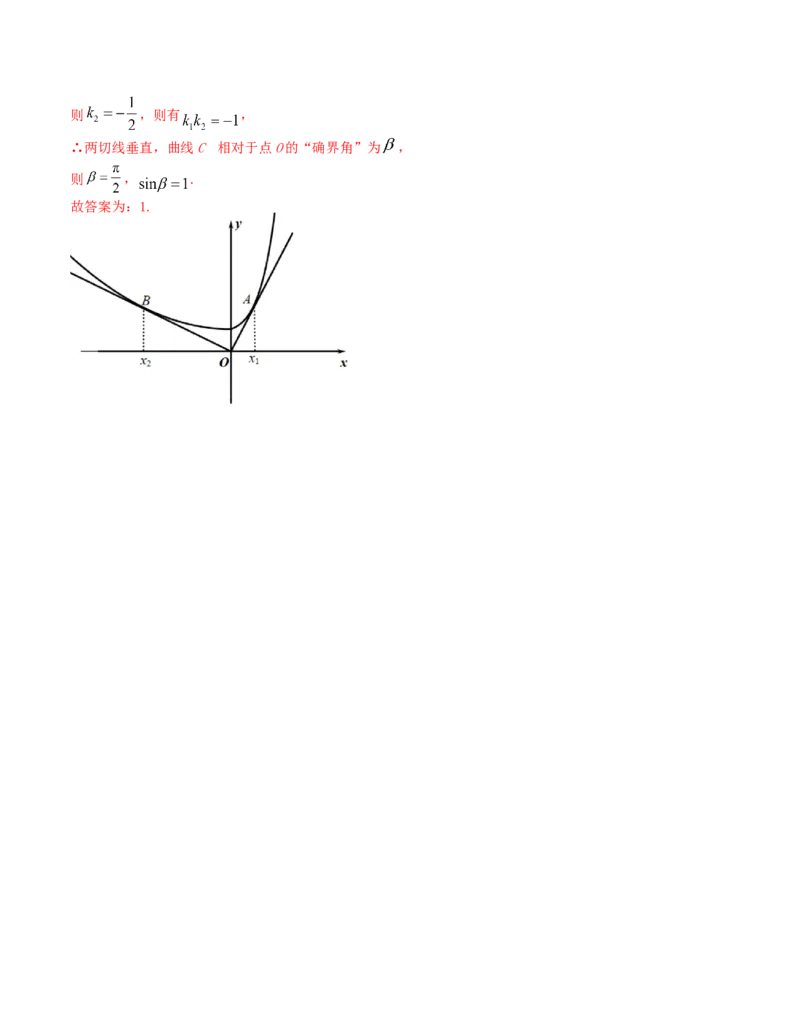
∴两切线垂直,曲线C 的相对于点O的“确界角”为 ,
则 , .
故答案为:1.