文档内容
高三年级 10 月考试数学试题
考试时间:120分钟 试卷满分:150分 命题、审题:高三数学备课组
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一个
选项是正确的.
1. 在复平面内, 的共轭复数对应的点位于( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
2. 集合 ,则满足 的集合 的个数为( )
A. 4 B. 7 C. 15 D. 16
3. 若双曲线 的两条渐近线的夹角为 ,则该双曲线的离心率为( )
A. B. 2 C. 2或 D. 或
4. 将函数 的图象向左平移 个单位长度后,所得的图象关于原点对称,则 的
最小值为( )
A. B. C. D.
5. 已知定义在 上的偶函数 ,且当 时, 单调递减,则关于 的不
等式 的解集是( )
A. B.
C. D.
6. 如图,一条河两岸平行,河的宽度为 ,一艘船从河岸边的 地出发,向河对岸航行.已知船在静
第1页/共6页
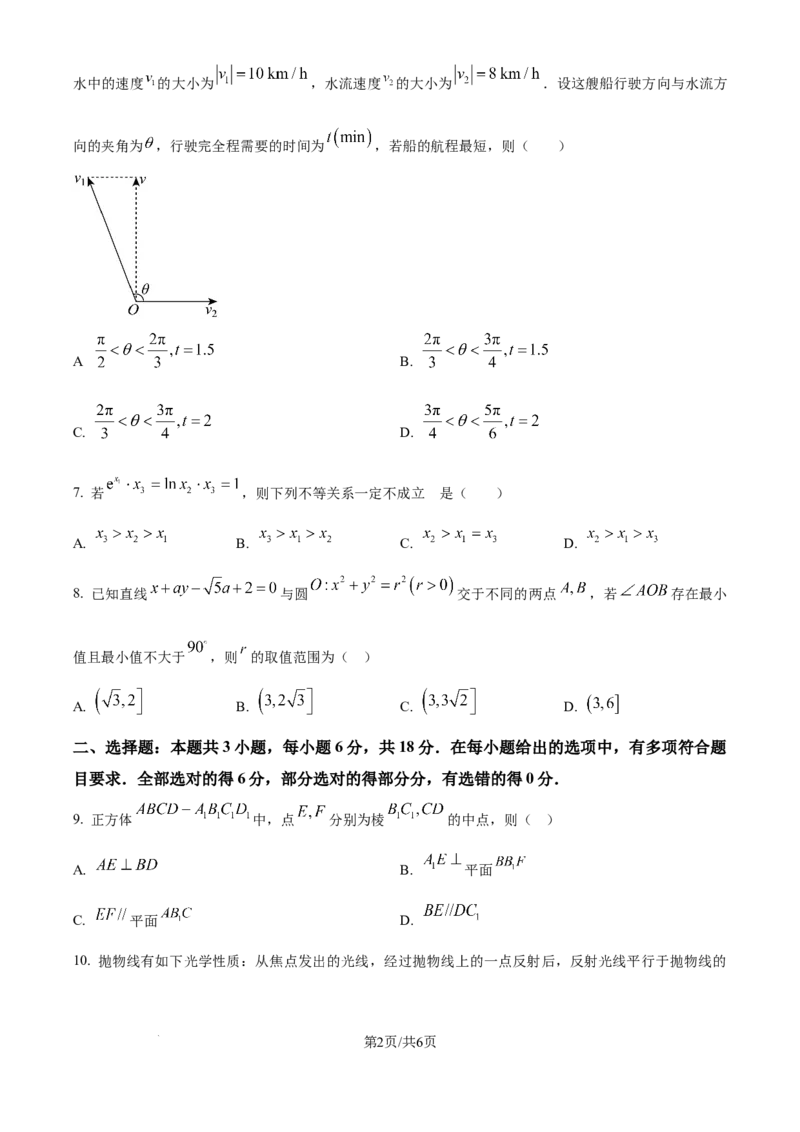
学科网(北京)股份有限公司水中的速度 的大小为 ,水流速度 的大小为 .设这艘船行驶方向与水流方
向的夹角为 ,行驶完全程需要的时间为 ,若船的航程最短,则( )
.
A B.
C. D.
的
7. 若 ,则下列不等关系一定不成立 是( )
A. B. C. D.
8. 已知直线 与圆 交于不同的两点 ,若 存在最小
值且最小值不大于 ,则 的取值范围为( )
A. B. C. D.
二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题
目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.
9. 正方体 中,点 分别为棱 的中点,则( )
A. B. 平面
C. 平面 D.
10. 抛物线有如下光学性质:从焦点发出的光线,经过抛物线上的一点反射后,反射光线平行于抛物线的
第2页/共6页
学科网(北京)股份有限公司轴;一束平行于抛物线的轴的光线,经过抛物线的反射集中于它的焦点.已知抛物线 为坐
标原点,一条平行于 轴的光线 从点 射入,经过 上的点 反射,再经过 上的另一点 反射
后沿直线 射出,则( )
.
A
B. 是一个钝角三角形
C. 若延长 交直线 于点 ,则点 在直线 上
D. 抛物线 在点 处的切线分别与直线 、 所成的角相等
11. 在 中, 是角 的对应边,满足 ,下列说法正确的
是( )
A.
B. 的最小值为2
C. 的面积最大值为
D. 若 ,则
三、填空题:本大题共3小题,每小题5分,共15分.
12. 若曲线 在点 处的切线也是曲线 的切线,则 _____.
13. 已知等差数列 的前 项和为 ,且 ,等比数列 的首项为 ,若 ,则
的值为_____.
14. 抛掷一枚质地均匀的正四面体骰子(四个面上分别标有数字1,2,3,4),底面的点数为1记为事件
第3页/共6页
学科网(北京)股份有限公司,抛掷 次后事件 发生奇数次的概率记为 ,则 _____, _____.
四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.
15. 某种疾病分为甲、乙两种类型,为研究该疾病的类型与患者性别是否有关,随机抽取了 名患者进行
调查,得到如下列联表:
疾病类型
性别 合计
甲型病 乙型病
男
女
合计
(1)根据小概率值 的独立性检验,得出了“所患疾病的类型与性别有关”的结论,求 的最小
值;
(2)现对部分人群接种预防甲型疾病的疫苗,要求每人至多安排2个周期接种疫苗,每人每周期必须接种
3次,每次接种后,产生抗体的概率为0.8.如果一个周期内至少2次产生抗体,那么该周期结束后终止接
种,否则进入第二个周期.已知每人每周期接种费用为30元,试估计1000人接种疫苗总费用的期望.附
,
.
001 0.005 0.001
6.635 7.879 10.828
16. 设数列 的前 项和为 ,且 .
(1)证明: 为等差数列;
第4页/共6页
学科网(北京)股份有限公司(2)数列 满足 ,当 ,且 时,求 的最小值.
的
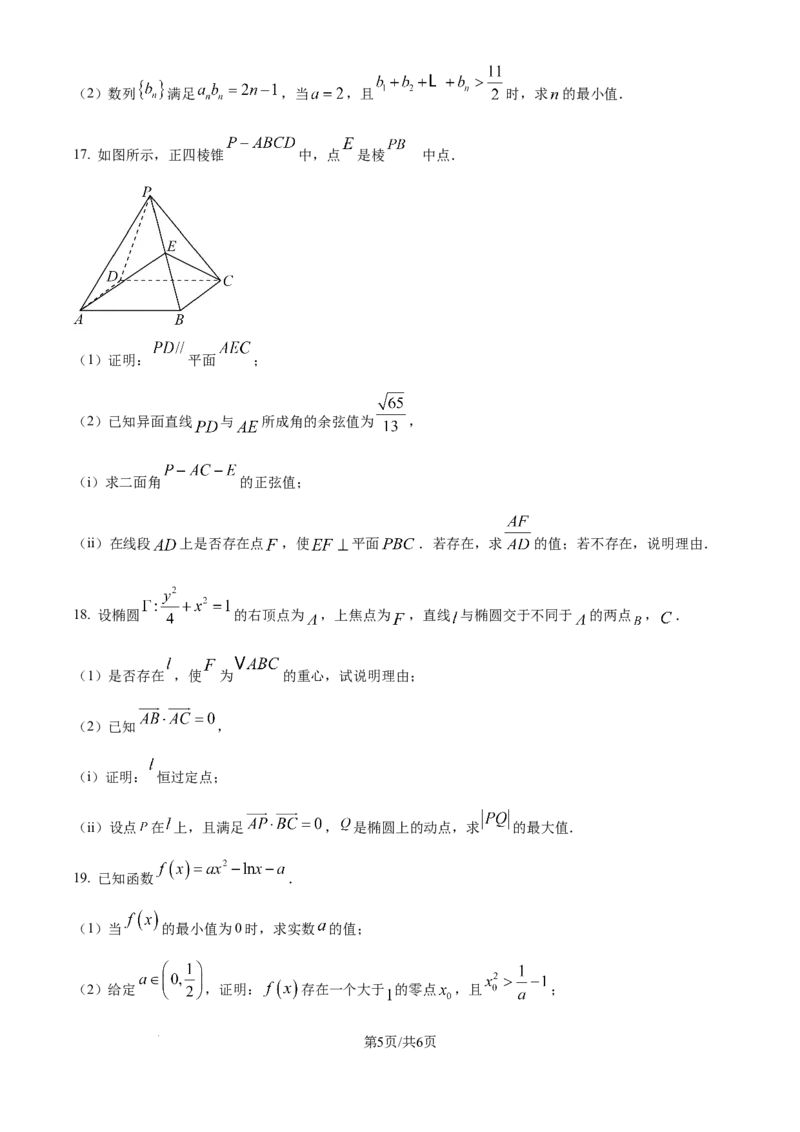
17. 如图所示,正四棱锥 中,点 是棱 中点.
(1)证明: 平面 ;
(2)已知异面直线 与 所成角的余弦值为 ,
(i)求二面角 的正弦值;
(ii)在线段 上是否存在点 ,使 平面 .若存在,求 的值;若不存在,说明理由.
18. 设椭圆 的右顶点为 ,上焦点为 ,直线 与椭圆交于不同于 的两点 , .
(1)是否存在 ,使 为 的重心,试说明理由;
(2)已知 ,
(i)证明: 恒过定点;
(ii)设点 在 上,且满足 , 是椭圆上的动点,求 的最大值.
19. 已知函数 .
(1)当 的最小值为0时,求实数 的值;
(2)给定 ,证明: 存在一个大于 的零点 ,且 ;
第5页/共6页
学科网(北京)股份有限公司(3)若对任意 ,都有 ,求实数 的取值范围.
第6页/共6页
学科网(北京)股份有限公司