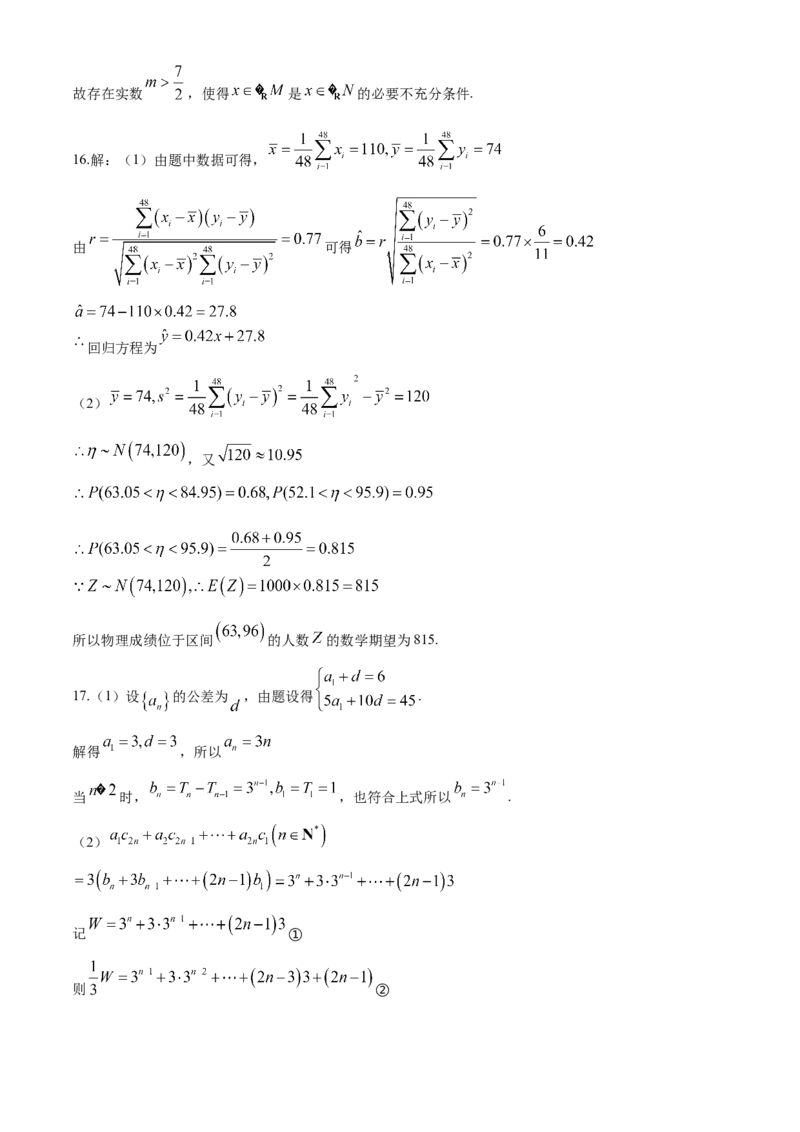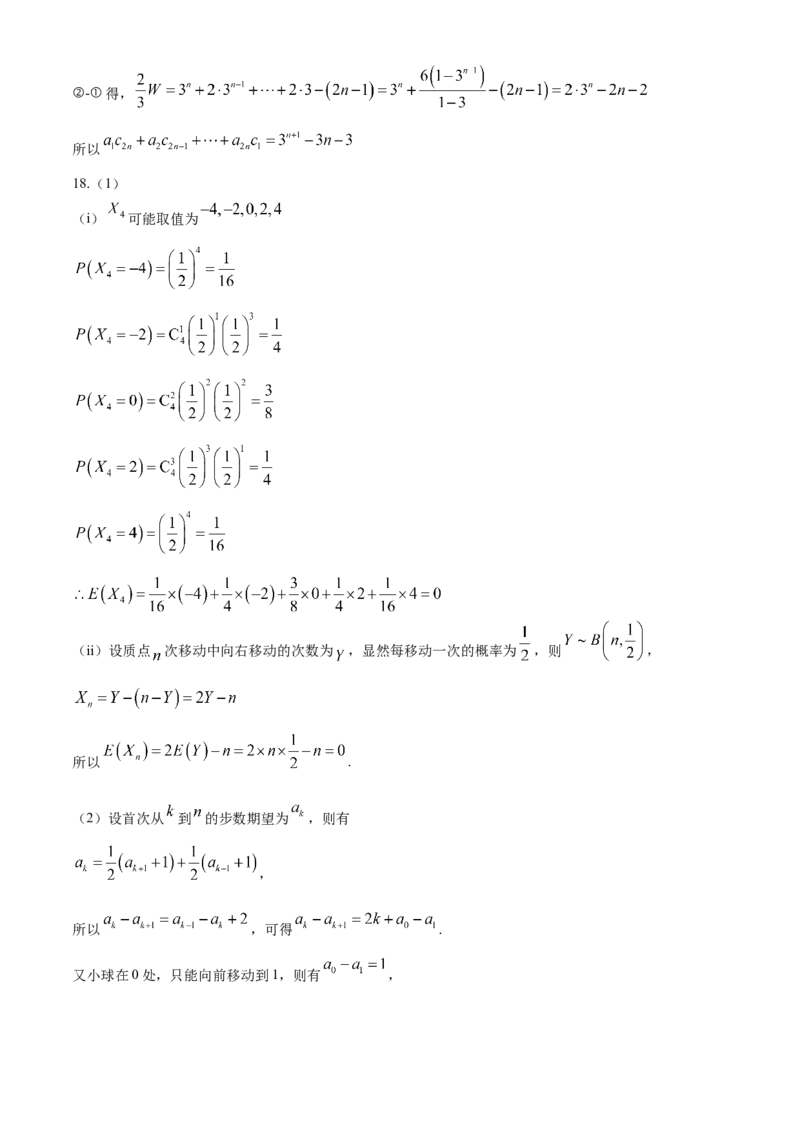文档内容
2023~2024 学年度第二学期期末质量检测
高二数学试卷
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是
符合题目要求的.
1.已知集合 ,则 ( )
A. B.
C. D.
2.设 ,则“ ”是“ ”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
3.若随机变量 ,且 ,则 的值为( )
A. B. C. D.
4.某人研究中学生的性别与成绩、视力、智商、阅读量这四个变量的关系,随机抽查32名中学生,得到如下4
个列联表,则与性别有关联的可能性最大的变量是( )
成绩
性别 合计
及格 不及格
男 14 6 20
女 22 10 32
合计 36 16 52
视力
性别 合计
及格 不及格
男 4 16 20
女 12 20 32
合计 16 36 52
智商
性别 合计
及格 不及格男 8 12 20
女 8 24 32
合计 16 36 52
阅读量
性别 合计
及格 不及格
男 14 6 20
女 2 30 32
合计 16 36 52
A.成绩 B.视力 C.智商 D.阅读量
5.已知 ,且满足 ,则( )
A. 的最小值为48 B. 的最小值为
C. 的最大值为48 D. 的最大值为
6.定义“等方差数列”:如果一个数列从第二项起,每一项的平方与它的前一项的平方的差都等于同一个
常数,那么这个数列就叫做等方差数列,这个常数叫做该数列的方公差.设数列 是由正数组成的等方
差数列,且方公差为 ,则数列 的前 项和为( )
A. B. C. D.
7.某医院要派2名男医生和4名女医生去 三个地方义诊,每位医生都必须选择1个地方义诊,要求
每个地方至少有一名医生,且都要有女医生,同时男医生甲不去 地,则不同的安排方案为(
)
A.120种 B.144种 C.168种 D.216种
8.已知定义在 上的函数 ,设 的极大值和极小值分别为 ,则 的取
值范围是( )A. B. C. D.
二、多选题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目
要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.
9.已知变量 和变量 的一组成对样本数据 的散点落在一条直线附近,
,相关系数 ,线性回归方程为
,则( )
A.当 越大时,成对数据样本相关性越强
B.当 时,
C.当 时,成对样本数据 的相关系数 满足
D.当 时,成对样本数据 的线性回归方程 满足
10.已知 ,且 ,则( )
A. B. 使得
C. 可能大于0 D.
11.冒泡排序是一种计算机科学领域的较简单的排序算法,其基本思想是:通过对待排序序列
从左往右,依次对相邻两个元素 比较大小,若 ,则交
换两个数的位置,使值较大的元素逐渐从左移向右,就如水底下的气泡一样逐渐向上冒,重复以上过程直
到序列中所有数都是按照从小到大排列为止.例如:对于序列 进行冒泡排序,首先比较 ,需要交换1次位置,得到新序列 ,然后比较 ,无需交换位置,最后比较 ,又需要交换
1次位置,得到新序列 最终完成了冒泡排序,同样地,序列 需要依次交换
完成冒泡排序.因此, 和 均是交换2次的序列.现在对任一个包含 个不等实数的序列进
行冒泡排序 ,设在冒泡排序中序列需要交换的最大次数为 ,只需要交换1次的序列个数为 ,
只需要交换2次的序列个数为 ,则( )
A.序列 是需要交换3次的序列 B.
C. D.
三、填空题:本题共3小题,每小题5分,共15分.
12.若函数 为 的导函数,则 的值为__________.
13. 的展开式中 的系数为__________.(用数字作答)
14.设 是一个随机试验中的两个事件,且 ,则
__________.
四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.
15.(13分)
已知集合 ,非空集合 ,
(1)若 时,求 ;
(2)是否存在实数 ,使得 是 的必要不充分条件?若存在,求实数 的取值范围;若
不恶在,请说朋理由.
16.(15分)
树人中学对某次高三学生的期末考试成绩进行统计,从全体考生中随机抽取48名学生的数学
成绩 和物理成绩 ,得到一些统计数据: ,其中分别表示这48名同学的数学成绩和物理成绩, 与 的相关系数 .
(1)求 关于 的线性回归方程;
(2)从概率统计规律看,本次考试该校高三学生的物理成绩 服从正态分布 ,用样本平均数
作为 的估计值,用样本方差 作为 的估计值.试求该校高三共1000名考生中,物理成绩位于区间
的人数 的数学期望.
附:①回归方程 中:
②相关系数
③若 ,则
④
17.(15分)
已知等差数列 的前 项利为 ,数列 的前 项利为 .
(1)求数列 和 的通项公式;
(2)设数列 满足 求 .
18.(17分)
(1)如图,在一条无限长的轨道上,一个质点在随机外力的作用下,从位置0出发,每次向左或向右移动
一个单位的概率都为 ,设移动 次后质点位于位置 .( 求随机变量 的概率分布列及 ;
(ii)求 ;
(2)若轨道上只有 这 个位置.质点向左或右移动一个单位的概率都为 ,若在0处,则只
能向右移动.现有一个质点从0出发,求它首次移动到 的次数价期望.
19.(17分)
已知函数 .
(1)求函数 的单调区间;
(2)证明 时, ;
(3)若对于任意的 ,关于 的不等式 恒成立,求实数 的取值范围.2023~2024 学年度第二学期期末质量检测高二数学试卷
参考答案
1.C 2.B 3.B 4.D 5.A 6.A 7.D 8.B 9.BCD 10.AD 11.BCD
12. 13. 14.
15.解:(1)集合
当 时,非空集合
(2)假设存在实数 ,使得 是 的必要不充分条件,则 ⫋ ,即 ⫋ ,则
,解得 .故存在实数 ,使得 是 的必要不充分条件.
16.解:(1)由题中数据可得,
由 可得
回归方程为
(2)
,又
所以物理成绩位于区间 的人数 的数学期望为815.
17.(1)设 的公差为 ,由题设得 .
解得 ,所以
当 时, ,也符合上式所以 .
(2)
记 ①
则 ②②-①得,
所以
18.(1)
(i) 可能取值为
(ii)设质点 次移动中向右移动的次数为 ,显然每移动一次的概率为 ,则 ,
所以 .
(2)设首次从 到 的步数期望为 ,则有
,
所以 ,可得 .
又小球在0处,只能向前移动到1,则有 ,所以 .又有 ,则 .
19.解:(1)
当 时, ;当 时,
的增区间为 ,减区间为 .
(2)令
当 时, ;当 时,
当 时, 即
原不等式等价于
为 上的减函数,
只需证明 即
令
当 时, ,当 时,
原不等式成立.
(3)当 时,由(2)知 又原不等式在 上恒成立.
当 时,令 .
在 内必有零点,设为 ,则
而
综上所述实数 的取值范围是 .