2024届黑龙江省牡丹江协同发展共同体高三下第一次模拟数学(1)_2024年4月_024月合集_2024届黑龙江省牡丹江协同发展共同体高三下第一次模拟

高三学年考试 数 学 试 题 考试时间：120分钟 分值：150分 一、单项选择题：本大题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项 是符合题目要求的.  1 1. 已知集合A{sin ,eln3},B {3，1，0，，1},则 AB （ ） 2 3 1 1 A．{3，1} B. { ，1} C. {3，0} D．{0，} 3 3 2. 5名应届毕业生报考3所不同院校，每人报考且仅报考1所院校，则不同的报名方法种数是( ) A. 35 B. 53 C. A3 D. C3 5 5 3. 一份新高考数学试卷中有8道单项选择题，小李对其中5道题有思路，3道题完全没有思路。有 思路的题做对的概率是0.9，没有思路的题只能猜一个答案，猜对答案的概率为0.25，则小李从 这8道题目中随机抽取1道做对的概率为（ ） 79 3 21 5 A． B． C． D． 160 5 32 8 4. 已知i为虚数单位，复数z abi,a,bR且满足 zi  2 ，求点Z(a,b)到直线y  x3距 离的最大值为（ ） A. 0 B. 2 22 C. 2 D. 2 2 5. 酒驾是严重危害交通安全的违法行为，为了保障交通安全，根据国家有关规定：100mL血液中 酒精含量达到20～79mg的驾驶员即为酒后驾车，80mg及以上认定为醉酒驾车．假设某驾驶员 喝了一定量的酒后，其血液中的酒精含量上升到了0.6mg/mL．如果停止喝酒以后，他血液中酒 精含量会以每小时30%的速度减少，那么他至少经过几个小时才能驾驶？（结果取整数，参考数 据：lg30.48，lg70.85）（ ） A．2 B．3 C．4 D．5            6. 已知a,b,c为不共线的平面向量，b  c ，若abc 0，则b 在a方向上的投影向量为（ ） 1  1  1  1  A.  a B.  a C. a D. a 3 2 2 4 7. 已知g(x)=x3f(x)是定义在R 上的奇函数，且 f(x)在区间（，0]上单调递减，若关于实数 m的不等式 f(log m)+ f(log m)  2f(3)恒成立，则m的取值范围是（ ） 2 0.51 1 1 A. (0，] B. [8,) C. (0，]  [8,) D. (0，]  [8,) 3 3 8  x1ex,x1 8. 已知函数 f x ，gx2  f x2 af x1a．若gx有5个零点，则实 x24x3,x1 数a的取值范围为（ ） 3 3 3 3 A．( ，1) B．( ，1] C．[ ,1] D．[ ,1) 2 2 2 2 二、多项选择题：本大题共3小题，每小题6分，共18分.在每小题给出的四个选项中，有多项符 合题目要求. 全部选对的得6分，部分选对的得部分分，有选错误的得0分. 9. 下列说法中正确的是（ ） A.某射击运动员在一次训练中10次射击成绩（单位：环）如下： 6，5，7，9，6，8，9，9，7，5, 这组数据的下四分位数为9 B.若随机变量X ~ B (100, p )，且E(X) 20，则D(X) 16 1 C.若随机变量X ~ N (  ,2 )，且P(X 4)  P(X 2)  p，则P(2 X 1)   p 2 D.对一组样本数据(x ,y ),(x ,y ), (x ,y ),进行分析，由此得到的线性回归方程为： 1 1 2 2 n n yˆ b ˆ xaˆ，至少有一个数据点在回归直线上  10. 已知( ,0)为函数 f(x)asin2xcos2x的一个对称中心，则（ ） 6  A. a  3 B. 函数 y  f(x )为奇函数 6 7 5  C. 曲线 y  f(x)关于x 对称 D. 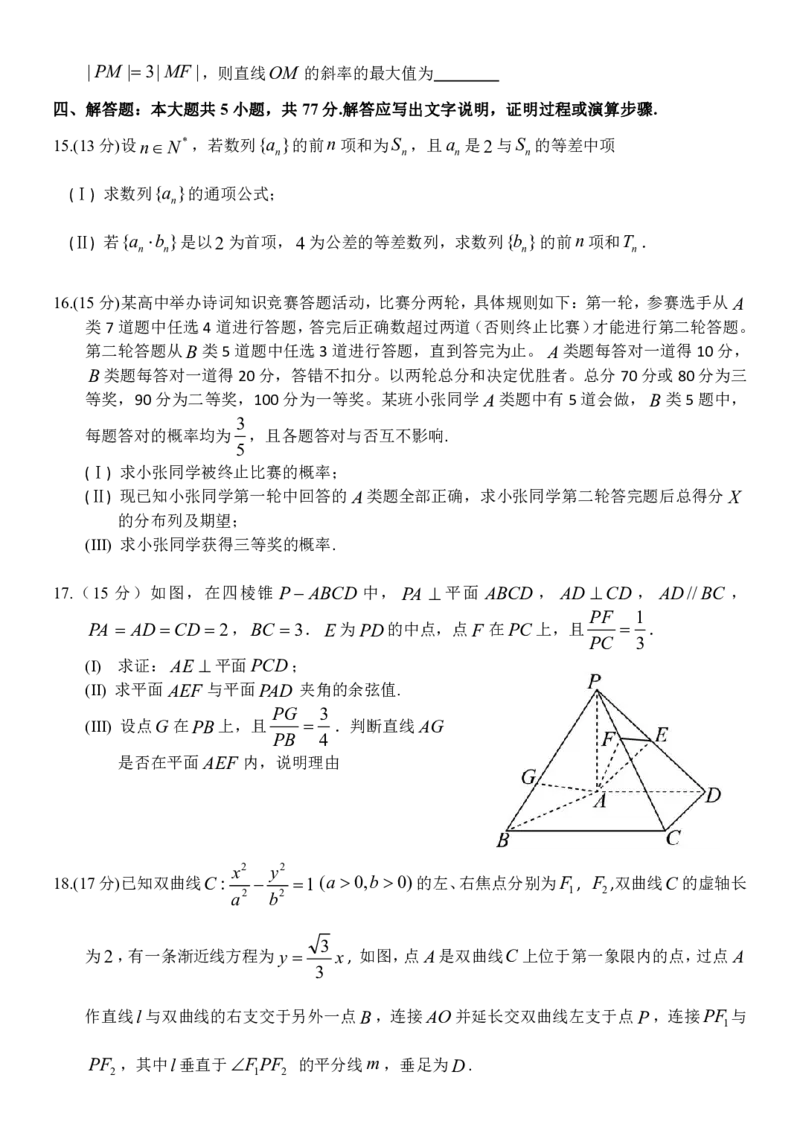函数 y  f(x)在( , )单调递增 12 12 12 11.如图，已知正方体ABCD ABC D 的棱长为2，P为底面ABCD内(包括边界)的动点，则下 1 1 1 1 列结论正确的是（ ） A.三棱锥B C D P的体积为定值 1 1 1 B．存在点P，使得D P  AC 1 1 C.若D P  B D，则P点在正方形底面ABCD内的运动轨迹长为 2 1 1 D.若点P是AD的中点，点Q是BB 的中点，过P，Q作平面平 1 面ACC A ，则平面截正方体ABCD ABC D 的截面面积为3 3 1 1 1 1 1 1 三、填空题：本大题共3小题，每小题5分，共15分. 12. 已知角的顶点与坐标原点重合，始边与x轴的非负半轴重合，点P(2,1)在终边上，则 cos2_____ 13. 已知(12x)5 a a xa x2 a x5,则a  (用数字作答) 0 1 2 5 3 14. 设O为坐标原点，P是以F 为焦点的抛物线 y2 4x上任意一点，M 是线段PF 上的点，且|PM |3|MF |，则直线OM 的斜率的最大值为 四、解答题：本大题共5小题，共77分.解答应写出文字说明，证明过程或演算步骤. 15.(13分)设nN*，若数列{a }的前n项和为S ，且a 是2与S 的等差中项 n n n n (Ⅰ) 求数列{a }的通项公式； n (Ⅱ) 若{a b }是以2为首项，4为公差的等差数列，求数列{b }的前n项和T ． n n n n 16.(15分)某高中举办诗词知识竞赛答题活动，比赛分两轮，具体规则如下：第一轮，参赛选手从A 类7道题中任选4道进行答题，答完后正确数超过两道（否则终止比赛）才能进行第二轮答题。 第二轮答题从B类5道题中任选3道进行答题，直到答完为止。A类题每答对一道得10分， B类题每答对一道得20分，答错不扣分。以两轮总分和决定优胜者。总分70分或80分为三 等奖，90分为二等奖，100分为一等奖。某班小张同学A类题中有5道会做，B类5题中， 3 每题答对的概率均为 ，且各题答对与否互不影响. 5 (Ⅰ) 求小张同学被终止比赛的概率； (Ⅱ) 现已知小张同学第一轮中回答的A类题全部正确，求小张同学第二轮答完题后总得分X 的分布列及期望； (Ⅲ) 求小张同学获得三等奖的概率. 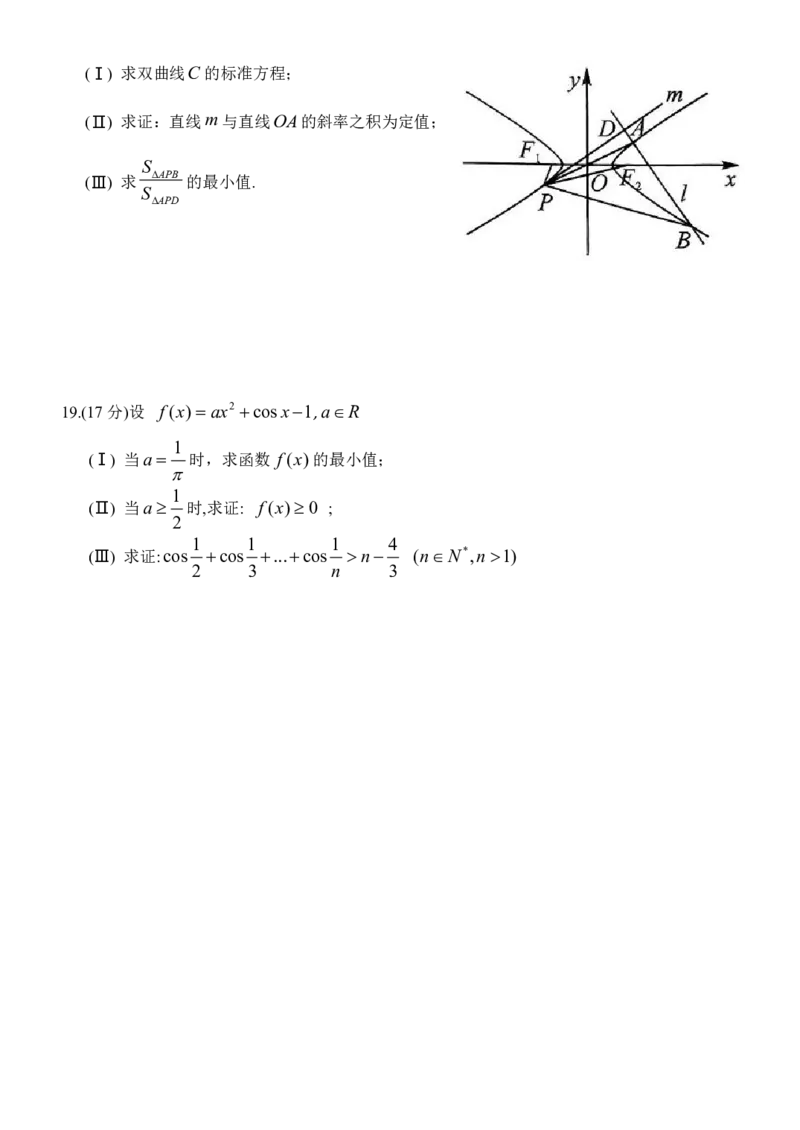17.（15 分）如图，在四棱锥 P ABCD 中， PA 平面 ABCD ， AD CD ， AD//BC ， PF 1 PA  AD CD 2，BC 3．E为PD的中点，点F 在PC上，且  ． PC 3 (Ⅰ) 求证：AE 平面PCD； (Ⅱ) 求平面AEF 与平面PAD 夹角的余弦值. 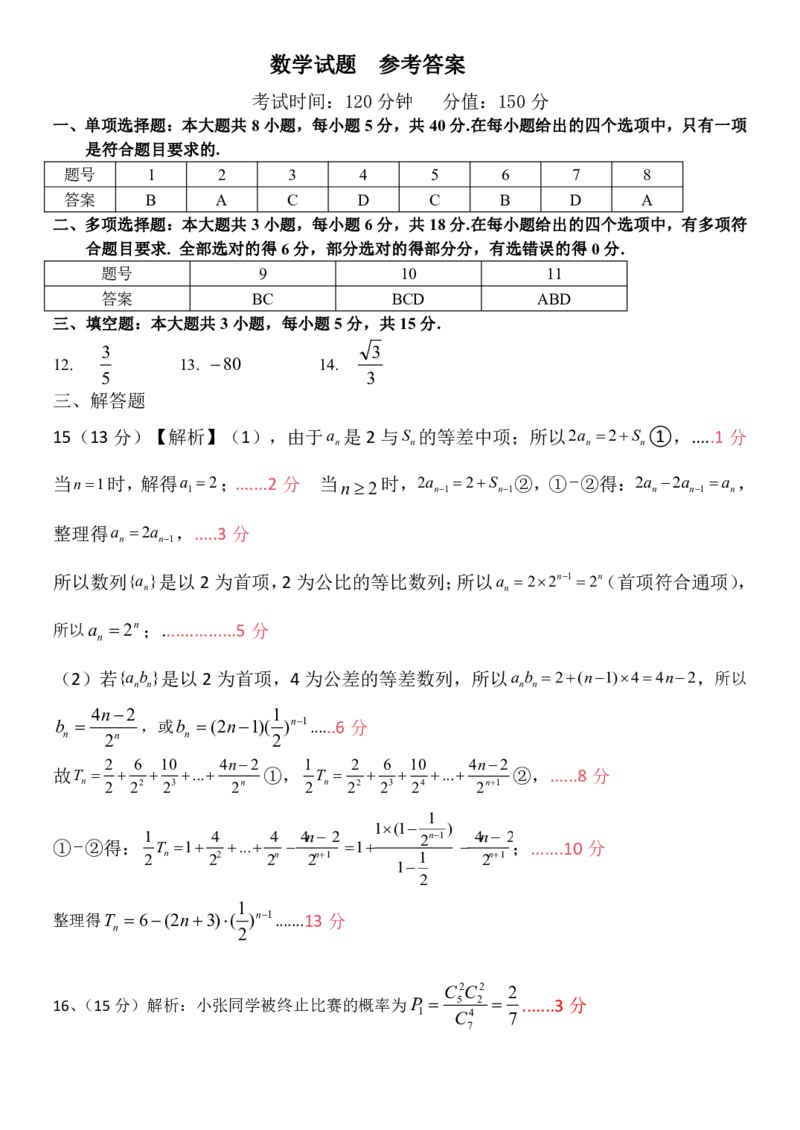PG 3 (Ⅲ) 设点G在PB上，且  ．判断直线AG PB 4 是否在平面AEF 内，说明理由 x2 y2 18.(17分)已知双曲线C:  1(a 0,b0)的左、右焦点分别为F , F ,双曲线C的虚轴长 a2 b2 1 2 3 为2，有一条渐近线方程为y  x, 如图，点A是双曲线C上位于第一象限内的点，过点A 3 作直线l与双曲线的右支交于另外一点B，连接AO并延长交双曲线左支于点P，连接PF 与 1 PF ，其中l垂直于FPF 的平分线m，垂足为D. 2 1 2(Ⅰ) 求双曲线C的标准方程； (Ⅱ) 求证：直线m与直线OA的斜率之积为定值； S (Ⅲ) 求 APB 的最小值. S APD 19.(17分)设 f(x)ax2 cosx1 aR 1 , (Ⅰ) 当a  时，求函数 f(x)的最小值；  1 (Ⅱ) 当a 时,求证: f(x)0 ; 2 1 1 1 4 (Ⅲ) 求证:cos cos ...cos n (nN*,n1) 2 3 n 3数学试题 参考答案 考试时间：120分钟 分值：150分 一、单项选择题：本大题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项 是符合题目要求的. 题号 1 2 3 4 5 6 7 8 答案 B A C D C B D A 二、多项选择题：本大题共3小题，每小题6分，共18分.在每小题给出的四个选项中，有多项符 合题目要求. 全部选对的得6分，部分选对的得部分分，有选错误的得0分. 题号 9 10 11 答案 BC BCD ABD 三、填空题：本大题共3小题，每小题5分，共15分. 3 3 12. 13. 80 14. 5 3 三、解答题 15（13分）【解析】（1），由于a 是2与S 的等差中项；所以2a 2S ①，.....1分 n n n n 当n1时，解得a 1 2；.......2 分 当 n2 时，2a n1 2S n1 ②，①②得：2a n 2a n1 a n ， 整理得a 2a ，.....3 分 n n1 所以数列{a }是以2为首项，2为公比的等比数列；所以a 22n1 2n（首项符合通项）， n n 所以a 2n；................5 分 n （2）若{a b }是以2 为首项，4 为公差的等差数列，所以a b 2(n1)44n2，所以 n n n n 4n2 1 b  ，或b (2n1)( )n1 ......6 分 n 2n n 2 2 6 10 4n2 1 2 6 10 4n2 故T    ... ①， T    ... ②，......8 分 n 2 22 23 2n 2 n 22 23 24 2n1 1 1(1 ) ①②得： 1 T 1 4 ... 4  4n 2 1 2n1  4n 2 ；.......10 分 2 n 22 2n 2n1 1 2n1 1 2 1 整理得T 6(2n3)( )n1 .......13分 n 2 C2C2 2 16、（15分）解析：小张同学被终止比赛的概率为P  5 2  .......3 分 1 C4 7 7(2)X的所有可能取值分别为40,60,80,100 2 8 3 2 36 P(X 40)C0( )3  ,P(X 60)C1( )( )2  3 5 125 3 5 5 125 3 2 54 3 27 P(X 80)C2( )2( ) ,P(X 100)C3( )3  3 5 5 125 3 5 125 ......8 分 分布列如下 X 40 60 80 100 8 36 54 27 P 125 125 125 125 8 36 54 27 E(X)40 60 80 100 76 125 125 125 125 .........10 分 (3)设小张张同学获得三等奖概率为P 2 C3C1 3 2 C4 3 2 54 P  5 2 C2( )2  5 C2( )2  2 C4 3 5 5 C4 3 5 5 175 7 7 .......... 15 分 17、（15分）（1）因为PA平面ABCD，又CD平面ABCD，则PACD， 又ADCD，且PAAD A，PA，AD平面PAD，故CD平面PAD； 又AE 面PAD,CD  AE,PA  AD,E为PD中点，AE  PD CDPD  D,CD,PD面PCD,AE 面PCD......5分 （2）过点 A 作AD的垂线交BC于点M ， 因为PA平面ABCD，且AM ，AD平面ABCD，所以PA AM ， PA AD， 故以点 为坐标原点，建立空间直角坐标系如图所示，..6分 A 则A0,0,0,B2,1,0,C2,2,0,D0,2,0,P0,0,2，    因为E为PD的中点，则E0,1,1，所以AE (0,1,1),PC (2,2,2),AP(0,0,2) ， PF 1  1 2 2 2    2 2 4 又  ，所以PF  PC ( , , )，故AF  APPF ( , , )， PC 3 3 3 3 3 3 3 3   yz0   nAE 0  设平面AEF 的法向量为n (x,y,z)，则   ，即2 2 4 ， nAF 0  x y z 0 3 3 3  令z1，则y1，x=1，故n(1,1,1)，....8分 又因为平面PAD的法向量为p(1,0,0)，     |n p| 3 所以cos|cosn, p |     ， |n|| p| 3 3 面AEF与面PAD夹角的余弦值为 ......10分 3 （3）直线AG不在平面AEF 内，....11分 PG 3   3 3 3 3 因为点G在 PB 上，且  ，又PB(2,1,2)，故PG PB( , , )， PB 4 4 2 4 2    3 3 3 3 3 1  则AGAPPG(0,0,2)( , , )( , , ) ，由（2）可知，平面AEF 的法向量为n(1,1,1)， 2 4 2 2 4 2   3 3 1 所以AGn   0，所以直线AG不在平面AEF 内．....15分 2 4 2 （第三问，通过共面向量基本定理且有一个公共点的证明方法，同样给分） 18.（17 分）解析 (1)因为虚轴长为2, 即: 所以 2 = 23, = 1. 又因为有一条渐近线方程为 y  x，所以a  3 3 x2 所以双曲线C的标准方程为  y2 1. ...3’ 3 (2)由题意，点 A 与点 P 关于原点对称. 设A(x ,y ) 则 P(x ,y ) 0 0 0 0 由题意可知直线m的斜率存在，设直线 m的斜率为k, ,    PF a PF a 记a (1,k)，又直线m为 的平分线，则 1  2 ...6 |PF | |PF | 1 2 ∠ ₁ ₂ ’ x2 因为 0  y2 1 ，所以x  3 3 0 0 所以 2 2 2 2 0 2 3 同理 | 1| = −2+ 0 + 0 = −2+ 0 ...9 + 3 −1 = 3 0 − 3, 2 3 | 2| = 3 0 + 3. ’  PF a PF a 又PF (x 2,y )，PF (x 2,y )，代入 1  2 得, 1 0 0 2 0 0 |PF | |PF | 1 2 (x 2,y )(1,k) (x 2,y )(1,k) 0 0 0 0 2 3  2 3 ， 化简得x 3ky x  3 x  3 0 0 3 0 3 0 y 1 所以k k  0 k  ，即直线 OA与直线m 的斜率之积为定值. ...11 OA x 3 0 ’ (3)由(2)可知 又 所以 , 将 代₀入= 3 ₀. ₀ > 0, ₀ >得0, , > 0 2 0 2 3 1 所以 ₀ = 3 ₀ 3 − 0 = 1, 0 > 3 0 = 3 2 −1, 0 = 3 2 −1, 3 1 3 1 3 设直线 m的3 2 方−1程3为 2 −1 , (− 2,将 2 −1,− 3 2 −1), > 3 . 代 入 得 n 3 1 2 所以直线m的方程 为 = + − 3 2 −1− 3由 2 点−1到直线距离公 = 式得 3 ， −1, 3 2 3k2 1 = + 3 −1, > 3 . |  3k2 1| 3k2 1 2 3k2 1 | AD|   ...13 k2 1 k2 1 ’ 又直线 AB 的斜率为 设直线 AB 的方程为 , 1 将 代 − 入 得 , 所以直线 A = B − 的 方 + 程 为 3 1 4 4 将其 与 3 2 −1 3 2 −1 联立 得 = 3 2 −1, = 。 − + 3 2 −1. 2 2 2 2 8 7 +3 设 3 − = 1 0)则 ²−3 ²− 3 2 −1 +3 2 −1 = 0 ...15 2 2 8 7 +3 由 ₁ ₁ 得 , ₂ ₂ , ₁+ ₂ = 2 −3 3 2 −1, 1 2 = 2 −3 3 2 −1 . ’ 2 1 ₁ ₂ < 0 ∈ 3 3 , 所以 3 2 2 6 +1 2 2 2 | | = 1+ | 1 − 2| = 1+ 1 + 2 −4 1 2 = 3− 2 3 2 −1. 所以 2 2 2 2 | | 3 +1 3 +1 当且仅 当 = | | = 3− 2 3 2 −即1 ≥ 2 +1 时 2 等=号3,成立， 所以当且仅3当− ² = 3 时²,−1, 的最 ²小=值1为3. ...17 = 1 ’19. （17分）解析(1)因为 的定义域为 R, 且 ( ) ，所以 为偶函数, 下面 取− = 。−当 ²+ 时 ,− −1 = ²+ 则−1 = ( ) ( ) 2 1 ' 2 当 时≥ , 0 = = +cos 可−知1, 在 = −上sin单 ,调递增， ' 2 > 2 时 ，令 = −sin > 当 1 则 −sin ≥ 0, ( ) 可知2+∞ 在 上单调递增. ' ' 2 ' 因 0 为 ≤ ≤ 2 则∃ = , 使得 = − 当 cos , 时 , 02 2 2 ' 当 0 < < 时 1, , 0 ∈ 0 所2以 , 在 cos 0 = 上 . 单调 递 ∈ 减 0 ,在 ₀ 上 < 单 0 调 ; 递增，且 ' ∈ 0 2 > 0; ( ) [0,x₀) 0 2 则 0 = 2 = 0, 在 内恒成立，可知 在 上单调递减. ' 综上 所 述 = , 在 ≤ 0 上 0 单2调递减，在 ( 上 ) 单调 0 递2 增， 所以 在 ( [ 0, ) +∞)上 0 的2 最小值为 2+∞ 又因为 ( ) 为偶函数，所以 在 R 2 内=的4−最1小. 值为 ...5 (2)由(1) 可( 知) 是定义在 (上 )的偶函数,下面取 4,−1. ’ 可知 令 ( ) x ≥ 0 ' ' 因为 =则2 − , = = 2 −则 . 在[ 上单调递增，可得 1 ' ≥ 2, 即 = 2 − 在 ≥ 1− 上 恒 成≥立0,， ( ) 0+∞ ' 可知 ≥ 在 0 [= 0, 上 单调 ≥ 递 0 增， 0+∞ 所以 ( ) 在 0+∞ 上的最小值为 结合偶函数性质可知 ...11 (3)由( 2() 可) 得0,当+∞ 时, 0 = 0, -1≥0,当且仅当 x= 0 时≥,0等. 号成立’,即 1 1 2 = 2 = 2 +cos 1 2 c 令 os ≥ 1−2 . 则 1 ∗ 1 1 2 = , ≥ 2, ∈ , cos > 1−2 ,当 时, 1 1 2 2 1 1 2 2 2 即 n ≥ 2 cos > 1−2 = 1−4 > 1− 4 −1 = 1− 2 −1−2 +1 , 1 1 1 则 cos > 1− 2 −1−2 +1 , 1 1 1 1 1 1 1 1 1 相加 co 可 s 得2 > 1− 3−5 ,cos3 > 1− 5−7 ,⋯,cos > 1− 2 −1−2 +1 , 1 1 1 1 1 4 1 因为 co则s2+cos3+⋯所+以c c o o s s 1> co s −1  1 ... − co 3 s −1 2 + n 1 4= −3+2 +1. 2 3 n 3 1 ≥ 2, 2 +1 > 0, 1 1 1 4 即 cos cos ...cos n (nN*,n1) ...17 2 3 n 3 ， ’