江苏省常州市第一中学2023-2024学年高二下学期6月月考试题数学Word版含解析_6月_240619江苏省常州市第一中学2023-2024学年高二下学期6月月考

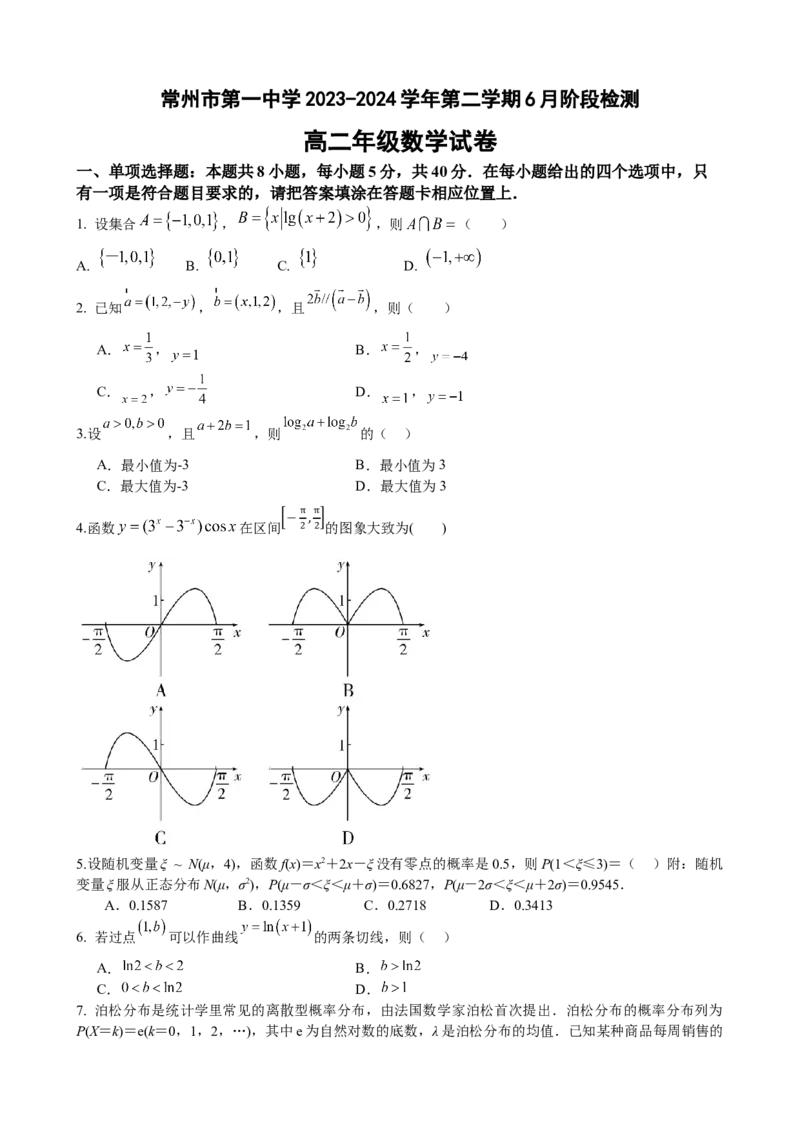
常州市第一中学2023-2024学年第二学期6月阶段检测 高二年级数学试卷 一、单项选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只 有一项是符合题目要求的，请把答案填涂在答题卡相应位置上． 1. 设集合 ， ，则 （ ） A. B. C. D. 2. 已知 ， ，且 ，则（ ） A． ， B． ， C． ， D． ， 3.设 ，且 ，则 的（ ） A．最小值为-3 B．最小值为3 C．最大值为-3 D．最大值为3 4.函数 在区间 的图象大致为( ) 5.设随机变量ξ ~ N(μ，4)，函数f(x)＝x2＋2x－ξ没有零点的概率是0.5，则P(1＜ξ≤3)＝（ ）附：随机 变量ξ服从正态分布N(μ，σ2)，P(μ－σ＜ξ＜μ＋σ)＝0.6827，P(μ－2σ＜ξ＜μ＋2σ)＝0.9545． A．0.1587 B．0.1359 C．0.2718 D．0.3413 6. 若过点 可以作曲线 的两条切线，则（ ） A． B． C． D． 7. 泊松分布是统计学里常见的离散型概率分布，由法国数学家泊松首次提出．泊松分布的概率分布列为 P(X＝k)＝e(k＝0，1，2，…)，其中e为自然对数的底数，λ是泊松分布的均值．已知某种商品每周销售的件数相互独立，且服从参数为λ(λ＞0)的泊松分布．若每周销售1件该商品与每周销售2件该商品的概率 相等，则两周共销售2件该商品的概率为（ ） A． B． C． D． 8. 已知函数 的定义域为 ，且满足 ， 的导函数为 ，函数 为奇函数，则 =（ ） A．-3 B．3 C．-1 D．1 二、多项选择题：本题共3小题，每小题6分，共18分，在每小题给出的选项中，有多项 符合题目要求．全部选对的得6分，部分选对的得部分分，有选错的得0分，请把答案填涂 在答题卡相应位置上． 9.下列说法正确的是 （ ） A．“x>2”是“<”的充分不必要条件 B．命题“ ” 的否定是 C．已知幂函数 的图象过点 ，则 = D．已知随机变量 服从两点分布，且 ， ，令 ，则 10. 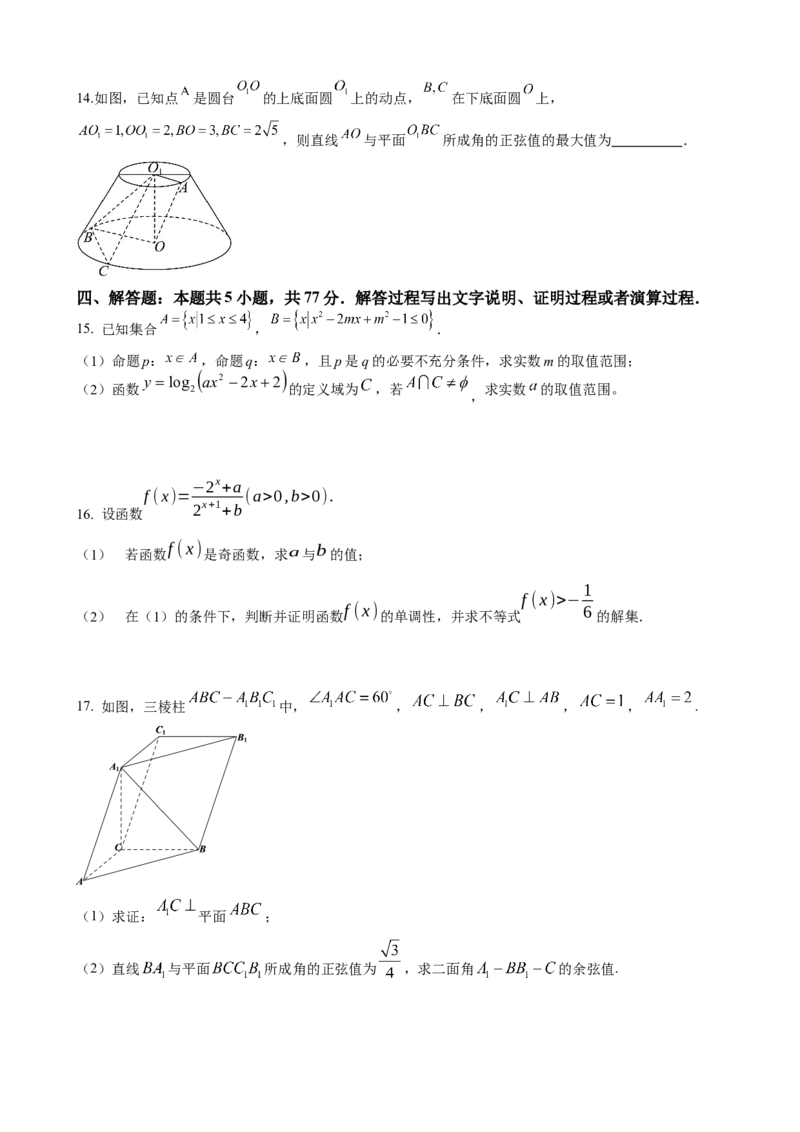如图，已知斜三棱柱 中， ， ， ， ， ，点 是 与 的交点.下列选项中正确的有 ( ) A． B． C．直线 与 所成的角的余弦值为 D．平面 与平面 不垂直 11.在一个有限样本空间中，假设 ，且A与B相互独立，A与C互斥，则（ ） A． B． C． D．若 ，则 三、填空题：本题共3小题，每小题5分，共15分． 12.某保险公司将其公司的被保险人分为三类：“谨慎的”“一般的”“冒失的”．统计资料表明，这三 类人在一年内发生事故的概率依次为0.05,0.15,0.30.若该保险公司的被保险人中“谨慎的”被保险人占 20%，“一般的”被保险人占50%，“冒失的”被保险人占30%，则该保险公司的一个被保险人在一年内 发生事故的概率是 ． 13.若不等式 ＋ ≥ 在x∈( ，2)上恒成立，则实数 的取值范围为 ．14.如图，已知点 是圆台 的上底面圆 上的动点， 在下底面圆 上， ，则直线 与平面 所成角的正弦值的最大值为 ． 四、解答题：本题共5小题，共77分．解答过程写出文字说明、证明过程或者演算过程． 15. 已知集合 ， ． （1）命题p： ，命题q： ，且p是q的必要不充分条件，求实数m的取值范围；   y log ax2 2x2 （2）函数 2 的定义域为 ，若 求实数 的取值范围。 ， −2x +a f (x)= (a>0,b>0). 16. 设函数 2x+1 +b （1） 若函数 f (x) 是奇函数，求a与 b 的值； 1 f (x)>− f (x) 6 （2） 在（1）的条件下，判断并证明函数 的单调性，并求不等式 的解集． 17. 如图，三棱柱 中， ， ， ， ， . （1）求证： 平面 ； （2）直线 与平面 所成角的正弦值为 ，求二面角 的余弦值.18.在某数字通信中，信号的传输包含发送与接收两个环节．每次信号只发送0和1中的某个数字，由于 随机因素干扰，接收到的信号数字有可能出现错误，已知发送信号0时，接收为0和1的概率分别为 ， ；发送信号1时，接收为1和0的概率分别为 ．假设每次信号的传输 相互独立． (1)当连续三次发送信号均为0时，设其相应三次接收到的信号数字均相同的概率为 ，求 的最 小值； (2)当连续四次发送信号均为1时，设其相应四次接收到的信号数字依次为 ，记其中连续出现相 同数字的次数的最大值为随机变量 （ 中任意相邻的数字均不相同时，令 ），若 ， 求 的分布列和数学期望． 19. 已知函数 ， ． （1）若函数 依次在 处取到极值． ①求 的取值范围； ②若 ，求 的值． （2）若存在实数 ，使对任意的 ，不等式 恒成立．求正整数 的最大值．常州市第一中学2023-2024学年第二学期6月阶段检测 高二数学答案与解析 一、单项选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只 有一项是符合题目要求的，请把答案填涂在答题卡相应位置上． 1. 设集合 ， ，则 （ ） A. B. C. D. 【答案】B 3. 已知 ， ，且 ，则（ ） A． ， B． ， C． ， D． ， 【答案】B 【分析】利用向量平行的充要条件列出关于x、y的方程组，解之即可求得x、y的值. 【详解】因为 ， ， 所以 ， 由 ，可得 ，解之得 故选：B 3.设 ，且 ，则 的（ ） A．最小值为-3 B．最小值为3 C．最大值为-3 D．最大值为3 【答案】C 【分析】由已知结合基本不等式先求 的范围，然后结合对数的运算性质即可求解. 【详解】因为 ，且 ， 所以 ，即 ， 当且仅当 时取等号， 所以 ，即 . 故选：C. 4.函数 在区间 的图象大致为( ) 答案 A 5.设随机变量ξ ~ N(μ，4)，函数f(x)＝x2＋2x－ξ没有零点的概率是0.5，则P(1＜ξ≤3)＝（ ）附：随机 变量ξ服从正态分布N(μ，σ2)，P(μ－σ＜ξ＜μ＋σ)＝0.6827，P(μ－2σ＜ξ＜μ＋2σ)＝0.9545． A．0.1587 B．0.1359 C．0.2718 D．0.3413 【答案】B 9. 若过点 可以作曲线 的两条切线，则（ ） A． B． C． D． 【答案】B 【分析】设切点点 ，写出切线方程，将点 代入切线方程得 ，此方程 有两个不同的解，利用导数求b的范围. 【详解】在曲线 上任取一点 ， ， 所以曲线 在点 处的切线方程为 . 由题意可知，点 在直线 上，可得 ， 令函数 ，令 10. 泊松分布是统计学里常见的离散型概率分布，由法国数学家泊松首次提出．泊松分布的概率分布列为 P(X＝k)＝e(k＝0，1，2，…)，其中e为自然对数的底数，λ是泊松分布的均值．已知某种商品每周销售的 件数相互独立，且服从参数为λ(λ＞0)的泊松分布．若每周销售1件该商品与每周销售2件该商品的概率 相等，则两周共销售2件该商品的概率为（ ） A． B． C． D． 【答案】D 【解析】由题意可知，P(X＝1)＝P(X＝2)，即e＝e，解得λ＝2，所以P(X＝k)＝e，所以两周共销售2件该 商品的概率2P(X＝0)P(X＝2)＋P(X＝1)P(X＝1)＝2ee＋ee＝，故答案选D． 11. 已知函数 的定义域为 ，且满足 ， 的导函数为 ，函数 为奇函数，则 =（ ） B A．-3 B．3 C．-1 D．1 二、多项选择题：本题共3小题，每小题6分，共18分，在每小题给出的选项中，有多项 符合题目要求．全部选对的得6分，部分选对的得部分分，有选错的得0分，请把答案填涂 在答题卡相应位置上． 9.下列说法正确的是 （ ） A．“x>2”是“<”的充分不必要条件 B．命题“ ” 的否定是 C．已知幂函数 的图象过点 ，则 = D．已知随机变量 服从两点分布，且 ， ，令 ，则 【答案】ACD 11. 如图，已知斜三棱柱 中， ， ， ， ， ，点 是 与 的交点.下列选项中正确的有( AC ) A． B． C．直线 与 所成的角的余弦值为 D．平面 与平面 不垂直11.在一个有限样本空间中，假设 ，且A与B相互独立，A与C互斥，则（ ） A． B． C． D．若 ，则 【答案】BCD 【分析】A与B相互独立，则 ,又因为 可判断A选项； 由条件概率的运算 判断B选项 ；因为A与C互斥，即A发生则C一定不发生，故 可判断C选项； ，即B与C互斥判断D. 【详解】对于A，A与B相互独立，则 , ，A错误； 对于B，因为A与C互斥，所以 ,所以 , , 所以 ,B正确； 对于C， ,因为A与C互斥，即A发生则C一定不发生， 所以 ,所以 ，C正确； 对于D，显然 ，即 ， 由 ，得 ， 解得 ，所以B与C互斥，D正确. 故选：BCD. 五、填空题：本题共3小题，每小题5分，共15分．12.某保险公司将其公司的被保险人分为三类：“谨慎的”“一般的”“冒失的”．统计资料表明，这三 类人在一年内发生事故的概率依次为0.05,0.15,0.30.若该保险公司的被保险人中“谨慎的”被保险人占 20%，“一般的”被保险人占50%，“冒失的”被保险人占30%，则该保险公司的一个被保险人在一年内 发生事故的概率是 0.175 ． 解：设事件B 表示“被保险人是‘谨慎的’”，事件B 表示“被保险人是‘一般的’”，事件B 表示 1 2 3 “被保险人是‘冒失的’”，则P(B)＝20%，P(B)＝50%，P(B)＝30%.设事件A表示“被保险人在一年 1 2 3 内发生事故”，则P(A|B)＝0.05，P(A|B)＝0.15，P(A|B)＝0.30.由全概率公式，得P(A)＝(B)P(A|B)＝ 1 2 3 i i 0.05×20%＋0.15×50%＋0.30×30%＝0.175. 13.若不等式 ＋ ≥ 在x∈( ，2)上恒成立，则实数 的取值范围为 ． 14.如图，已知点 是圆台 的上底面圆 上的动点， 在下底面圆 上， ，则直线 与平面 所成角的正弦值的最大值为 ． 【答案】 【分析】以 为坐标原点，建立空间直角坐标系，求得对应点的坐标，设出未知点的坐标，利用向量法求 线面角正弦值的最大值，再求余弦值的最小值即可. 【详解】连接 ，过 作 垂直于 的延长线于点 ，以 为坐标原点，建立空间直角坐标系如下所示： 在三角形 中，因为 ， 故 ，则 ， 则 ， ，故点 ； 又 ，设点 ，由 ，则可得 ；， 设平面 的法向量 ， 则 ，即 ，取 ，则 ， 故平面 的法向量 ，又 ， 设直线 与平面 所成角为 ， 则 因为 ，且 ，故令 ， 则 又 ，故 ， ，也即 ， 故 的最大值为 六、解答题：本题共5小题，共77分．解答过程写出文字说明、证明过程或者演算过程． 18. 已知集合 ， ． （1）命题p： ，命题q： ，且p是q的必要不充分条件，求实数m的取值范围；   y log ax2 2x2 （2）函数 2 的定义域为 ，若 求实数 的取值范围。 ， 【详解】（1）解不等式 ，即 ，解得 ， 所以， ． 由于p是q的必要非充分条件，则 是 的真子集，所以 ，解得 ， 因此，实数 的取值范围是 ； ┄ ┄ 6分 2 2 a    （2）因为 ， ax2 2x2 0 在 内有有解 x2 x令 ，则 ，所以 ┄ ┄ 13分 19. 设函数 （3） 若函数 是奇函数，求 与 的值； （4） 在（1）的条件下，判断并证明函数 的单调性，并求不等式 的解集． 解析： （1）由函数 是奇函数，得 ， −2−x +a =− 即 2−x+1 +b 对定义域内任意实数 都成立，化简整理得 ，它对定义域内任意实数 都成立， 所以 所以 或 经检验 符合题意． ………………………7分 （3）由（2）可知 由 易判断 为 上的减函数。证明略（定义法或导数法） 由 ，不等式 即为 ，由 为 上的减函数 可得 或者由 即 ， 所以 所以 ………………………15分 20. 如图，三棱柱 中， ， ， ， ， .（1）求证： 平面 ； （2）直线 与平面 所成角的正弦值为 ，求二面角 的余弦值. （1）证明：在 中， ， ， ， 由余弦定理可得 ， ， ， 又 ， ， 平面 ； ……………… 5分 （2）由（1）知： 、 、 两两垂直， 以 为原点， 、 、 所在直线分别为 、 、 轴建立如下图所示的空间直角坐标系， 则 、 、 ，设点 ，其中 ， 设平面 法向量为 ， ， ， ，取 ，则 ， ，得 ， ，由已知 ， 解得： ，可得点 ， 设 为平面 的法向量， ，由 ，取 ，则 ， ，可得 ， ， 由图可知，二面角 为锐角，所以，二面角 的余弦值为 . ………………………15分 18.在某数字通信中，信号的传输包含发送与接收两个环节．每次信号只发送0和1中的某个数字，由于 随机因素干扰，接收到的信号数字有可能出现错误，已知发送信号0时，接收为0和1的概率分别为 ， ；发送信号1时，接收为1和0的概率分别为 ．假设每次信号的传 输相互独立． (1)当连续三次发送信号均为0时，设其相应三次接收到的信号数字均相同的概率为 ，求 的最 小值； (2)当连续四次发送信号均为1时，设其相应四次接收到的信号数字依次为 ，记其中连续出现 相同数字的次数的最大值为随机变量 （ 中任意相邻的数字均不相同时，令 ），若 ， 求 的分布列和数学期望． 【答案】(1) (2)分布列见解析；期望为 【分析】（1）由独立乘法、互斥加法得函数 表达式，进一步即可求解最小值； （2） 的可能取值为1，2，3，4．有独立乘法、互斥加法公式求出对应的概率，进而得分布列以及数学 期望. 【详解】（1）由题可知 ， 因为 ，所以当 时， 的最小值为 ． …………5分 （2）由题设知， 的可能取值为1，2，3，4．①当 时，相应四次接收到的信号数字依次为0101或1010． 因此， ， ②当 时，相应四次接收到的信号数字依次为0010，或0100，或1101，或1011，或1001，或0110， 或1100，或0011． 因此， ， ③当 时，相应四次接收到的信号数字依次为1110，或0111，或0001，或1000． 因此， ， ④当 时，相应四次接收到的信号数字依次为0000，或1111． 因此， ． 所以 的分布列为 1 2 3 4 的数学期望 ． 答： 的数学期望为 …………17分 20. 已知函数 ， ． （1）若函数 依次在 处取到极值． ①求 的取值范围； ②若 ，求 的值． （2）若存在实数 ，使对任意的 ，不等式 恒成立．求正整数 的最大值． 解：（1）①…………5分 ② …………10分 （2）不等式 ，即 ，即 ． 转化为存在实数 ，使对任意的 ，不等式 恒成立． 即不等式 在 上恒成立． 即不等式 在 上恒成立． 设 ，则 ． 设 ，则 ，因为 ，有 ． 故 在区间 上是减函数． 又 故存在 ，使得 ． 当 时，有 ，当 时，有 ． 从而 在区间 上递增，在区间 上递减． 又 所以当 时，恒有 ；当 时，恒有 ； 故使命题成立的正整数 的最大值为5． …………17分