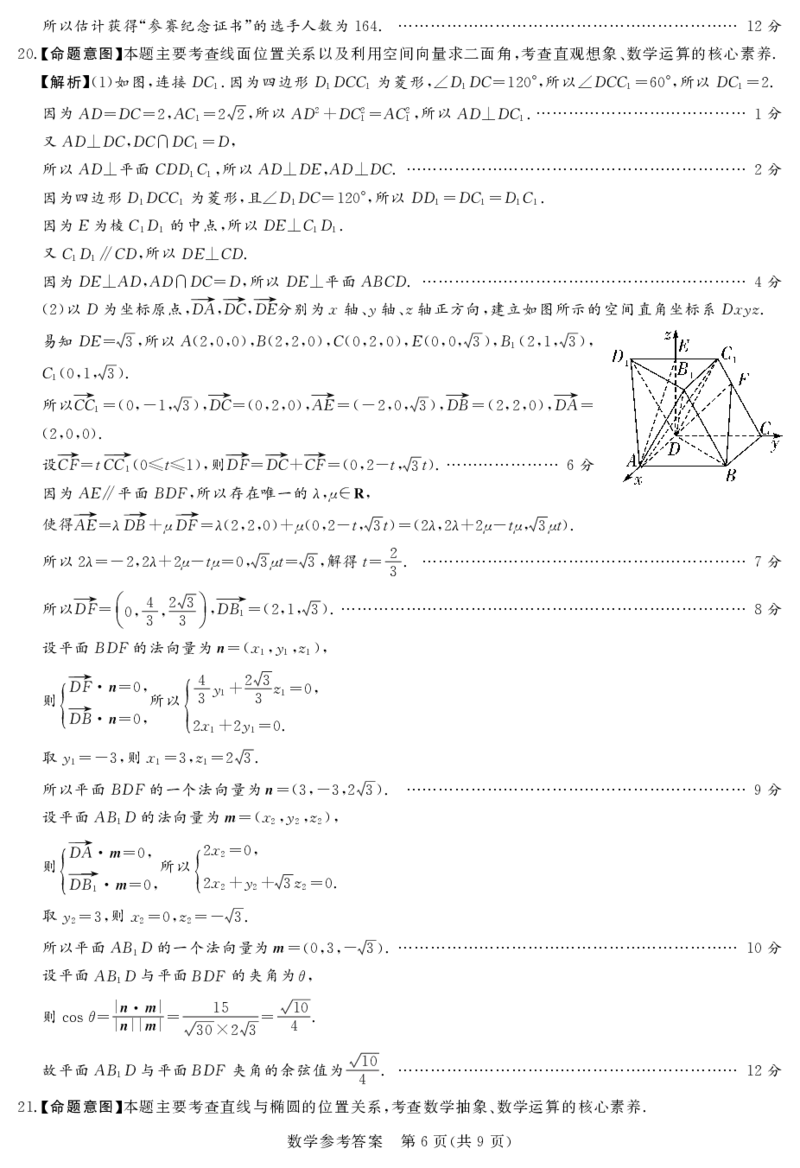文档内容
湘 豫 名 校 联 考
年 月高三第一次模拟考试
2024 2
数学参考答案
题号
1 2 3 4 5 6 7 8 9 10 11 12
答案
D C A B B D D A BC AC ACD BCD
一、选择题:本题共 小题,每小题 分,共 分 在每小题给出的四个选项中,只有
8 5 40 .
一项是符合题目要求的
.
. 【命题意图】本题考查集合的交集和补集的运算 考查数学运算的核心素养.
1D ,
{ }
【解析】由题意可得
∁
RA
=
[
2
,
+∞
),因为B
=
xy
=
1
x =
(
-∞
,
3
),所以(
∁
RA)
∩
B
=
[
2
,
3
).故选
D
.
3-
. 【命题意图】本题考查复数的运算 共轭复数的定义以及复数的几何意义 考查数学运算的核心素养.
2C 、 ,
3 1
【解析】因为z i+1= 1 ,所以z i=( 2)-(i )-1=- 3 - 1 i ,所以z = - 5 - 5 i =- 1 + 3 i ,所以z =
2+i 2+i 2-i 5 5 i 5 5
( )
1 3 ,所以z在复平面内对应的点的坐标为 1, 3 ,位于第三象限.故选 .
- - i - - C
5 5 5 5
. 【命题意图】本题考查平面向量的坐标运算以及反向共线满足的条件 考查数学运算的核心素养.
3A ,
【解析】因为a (, ),b (x, ),c ( ,x),所以 a b ( x, ),a c (, x).因为 a
= 1-2 = -1 = -4 2+ = 2+ -5 - = 5 -2- 2 +
b,a c共线,所以( x) ( x) ( ) ,解得x 或x .又 a b,a c反向共线,代入验
- 2+ × -2- - -5×5=0 =3 =-7 2+ -
证可知x 时为同向,舍去.x 满足条件.所以x .故选 .
=3 =-7 =-7 A
. 【命题意图】本题考查利用基本不等式求最值 考查数学运算 逻辑推理的核心素养.
4B , 、
【解析】由x ,y ,且1 1 ,可得xy x y.所以 xy x x y x x y.又因为x y
>0 >0 x+y=1 = + 4 -3 =4 +4 -3 = +4 +4 =
(x y) ( 1 1 ) 4 y x ,当且仅当4 y x ,即x ,y 3时取等号,所以 xy x .故选 .
+4 x+y =5+x+y≥9 x=y =3 = 4 -3 ≥9 B
2
. 【命题意图】本题主要考查等差数列 等比数列的求和 考查数学运算的核心素养.
5B 、 ,
【解析】因为a
1=
b
1+2=2
,所以b
1=0
.根据题意,cn= {
b
a
n
n
,
,
n
n
为
为
偶
奇
数
数,
=
{ 2
2 n
n,
-
n
2
为
,n
奇
为
数
偶
,
数,
n
∈
N* ,所以T
20=
( ) ( )
( 3 5 … 19 ) ( … ) 2× 1-4 10 10× 1+19 598+2 21 .故选 .
2+2+2+ +2 +21+3+5+ +19= +2× = B
1-4 2 3
. 【命题意图】本题考查排列组合的基本运算以及古典概型的概率 考查学生数学抽象 数学运算 数学建模
6D , 、 、
的核心素养.
【解析】 名志愿者分配到 个场馆,共有
2 4
种不同的方法,A,B两名志愿者在同一个场馆共有
4
种不同
5 4 C5A4 A4
的方法,所以A,B两名志愿者不在同一个场馆的概率为P A 4 4 9.故选 .
=1- 2 4= D
C5A4 10
. 【命题意图】本题主要考查三角函数单调性 周期性和对称性的综合 考查数学运算的核心素养.
7D 、 ,
【解析】因为f() φ ,所以 φ k π或 φ k 5π,k Z.又 φ π,所以 φ 5π,
0=2sin +1=0 =2π- =2π- ∈ -π< <- =-
6 6 2 6
( ) ( )
所以f(x) ωx 5π .因为f(x)的图象关于点 5π, 对称,所以5πω 5π k,k Z,所以ω
=2sin - +1 1 - = π ∈ =
6 36 36 6
36 k ,k Z.因为x [ ,π ] ,ω ,所以ωx 5π [ 5π,π ω 5π ] .又函数f(x)在 [ ,π ] 上单调,所
+6 ∈ ∈ 0 >0 - ∈ - - 0
5 18 6 6 18 6 18
数学参考答案 第 页 共 页
1 ( 9 )
{#{QQABAYQQggAoABAAAQhCAwU6CgIQkACAAKoGQAAIIAABiRNABAA=}#}{ ω
π 5π π,
以
18
-
6
≤-
2
解得
0<
ω
≤6
.因为ω
∈
N* ,所以当k
=0
时,ω
=6
.因为f(x)图象的相邻两条对称轴之
ω ,
>0
间的距离为半个周期,所以T 1 2π π.故选 .
= × = D
2 2 6 6
. 【命题意图】本题考查利用三角函数公式进行计算 利用导数求最值等基本知识 考查数学抽象 数学运
8A , , 、
算 逻辑推理的核心素养.
、
( )
【解析】 1 1 α ( 2α 2α) 1 1 α 3 2α 1 α.令t
2α+ 2α-tan = sin +cos 2α+ 2α -tan = +tan + 2α-tan =
2sin cos 2sin cos 2 2tan
α,因为α为锐角,所以t .令f(t) 3 t2 1 t,则f'(t) t 1,f″(t) 3 .所以
tan >0 = + +t2- =2-1-t3 =2+t4>0
2 2
f'(t)在t 时是单调递增函数.又f'() ,所以当t (,)时,f'(t) ,f(t)单调递减;当t (, )
>0 1=0 ∈ 01 <0 ∈ 1 +∞
时,f'(t) ,f(t)单调递增,所以f(t)f() .所以当t 时,f(t)的最小值为 .故选 .
>0 ≥ 1=2 >0 2 A
二、选择题:本题共 小题,每小题 分,共 分.在每小题给出的四个选项中,有多
4 5 20
项符合题目要求.全部选对的得 分,部分选对的得 分,有选错的得 分.
5 2 0
. 【命题意图】本题考查概率统计的基本知识 考查数学运算 数学建模 逻辑推理 数据分析的核心素养.
9BC , 、 、 、
【解析】若有一个经验回归方程
^
y
=1-2
x,随着x的增大,
^
y会减小,
A
错误;曲线关于x
=0
对称,因为P(ξ
>
2
)
=0
.
2
,所以P(ξ
<-2
)
=0
.
2
,所以P(
-2≤
ξ
≤2
)
=1-
P(ξ
>2
)
-
P(ξ
<-2
)
=0
.
6
,
B
正确;因为xi+ yi=
( )
10
,x
=
1
i∑
4xi ,y
=
1
i∑
4 yi ,所以x
+
y
=
1
i∑
4xi+ 1
i∑
4 yi= 1
i∑
4xi+i∑ 4 yi
=10
,所以s2
1=
4 =1 4 =1 4 =1 4 =1 4 =1 =1
(x x) 2 (x x) 2 (x x) 2 (x x) 2 x2 xx x2 x2 xx x2 … x2 xx x2
1- + 2- + 3- + 4- 1-21 + + 2-22 + + + 4-24 +
= =
4 4
x2
1+
x2
2+
x2
3+
x2
4-
(
2
x
1+2
x
2+2
x
3+2
x
4
)x
x2
x2
1+
x2
2+
x2
3+
x2
4 x2 x2
x2
1+
x2
2+
x2
3+
x2
4 x2 ,同理
+ = -2 + = -
4 4 4
可 得:s2 y2 1+ y2 2+ y2 3+ y2 4 y2 ( 10- x 1 ) 2 + ( 10- x 2 ) 2 + ( 10- x 3 ) 2 + ( 10- x 4 ) 2 ( x) 2
2 = - = - 10- =
4 4
400-20
(x
1+
x
2+
x
3+
x
4
)
+
x2
1+
x2
2+
x2
3+
x2
4 ( x) 2 x
x2
1+
x2
2+
x2
3+
x2
4 x x2
- 10- =100-20 + -100+20 - =
4 4
x2
1+
x2
2+
x2
3+
x2
4
-
x2 ,故s2
1=
s2
2
,
C
正确;经验回归方程为
^
y
=3
x
+^
a,且样本点(m,
3
)与(
2
,n)的残差相等,则
4
(m a)n ( a) m n , 错误.故选 .
3- 3 +^ = - 6+^ ⇒3 + =9D BC
. 【命题意图】本题根据正弦型函数的性质 图象的变换性质 结合已知图象逐一判断即可 考查三角函
10AC 、 , ,
数的基本运算以及其图象的应用 考查数学运算 直观想象 逻辑推理的核心素养.
, 、 、
( )
【解析】由题图知,A ,3T 5π π 3π,所以周期T ,ω 2π .所以f(x)在[,]上有两个
=2 = - - = =π = =2 0π
4 12 3 4 π
( ) ( )
极值点, 正确.又f5π 5π φ ,所以5π φ k π,k Z,所以 φ k π,k Z.因
A =2sin2× + =2 + =2π+ ∈ =2π- ∈
12 12 6 2 3
( ) ( ) ( )
为 φ π,所以令k ,即 φ π.所以f(x) x π .所以f 2π -2π π
||< =0 =- =2sin2 - - =2sin2× - =
2 3 3 3 3 3
, 错误.因为函数f(x)的周期为 ,将y f(x)图象上的所有点沿x轴向右平移π个单位长度后得到
3B π =
12
( ) ( ) ( )
y fx π x π x的图象,为偶函数,所以函数y fx π 的图象关于y轴对
= - =2sin2 - =-2cos2 = -
12 2 12
称, 正确.若f(x)f(x) ,则x x 的最小值为π, 错误 故选
C | 1 - 2|=4 |1- 2| D . AC.
2
数学参考答案 第 页 共 页
2 ( 9 )
{#{QQABAYQQggAoABAAAQhCAwU6CgIQkACAAKoGQAAIIAABiRNABAA=}#}. 【命题意图】本题主要考查双曲线的几何性质和基本不等式 考查数学运算 逻辑推理的核心素养.
11ACD , 、
【解析】双曲线C: x2 y2 的渐近线方程为y b x.设点A(x,y)到两条渐近线的距离分别为d,d,
a2-b2=1 =±a 1 2
则利用点到直线的距离公式可得dd | bx + ay |·| bx - ay | | (bx) 2 - (ay) 2 |.因为x2 y2 ,所以
1 2= a2
+
b2 a2
+
b2 = a2
+
b2 a2-b2=1
(bx) 2 (ay) 2 a2b2 ,所以dd | a2b2 | a2b2 3,所以1 1 2, 正确;因为1 1 2 2,
- = 1 2=a2 b2=a2 b2= a2+b2= A a2+b2= ≥ab
+ + 2 3 3
所以ab
≥3
,
B
错误;因为a2
+
b2
=
(a2
+
b2 ) (
a
1
2+b
1
2
)
×
3
2 =
(
2+
b
a
2
2+
a
b2
2 )
×
3
2 ≥
æ
è
ç
2+2
b
a
2
2
· a
b2
2 ö
ø
÷
×
( )
3 ,当且仅当a b时等号成立, 正确;因为 1 1 2 1 1 2 2 2 2 2 4,所以
=6 = C a+b =a2+b2+ab= +ab≤ + =
2 3 3 3 3
1 1 23,当且仅当a b时等号成立, 正确 故选
a+b≤ = D . ACD.
3
. 【命题意图】本题主要考查空间中线面位置关系 考查直观想象 数学运算的核心素养.
12BCD , 、
【解析】如 图,连 接 CE,EM.因 为 平 面 AEFD 平 面 EBCF,平 面 AEFD
⊥ ∩
平面EBCF EF,AE 平面AEFD,又AE EF,所以AE 平面EBCF.所以CE为
= ⊂ ⊥ ⊥
CA在平面EBCF内的射影.易得 BCF为等边三角形,显然CE不垂直于BF,所以
△
AC不可能垂直于BF, 错误.易知BE EF,所以BE 平面AEFD,所以 BME为
A ⊥ ⊥ ∠
直线MB与平面AEFD所成的角.同理 CMF为直线MC与平面AEFD所成的角.
∠
所以 BME CMF,所以 BME CMF,所以BE CF .因为CF BE,
∠ =∠ tan∠ =tan∠ EM=FM =2
所以FM EM.在平面AEFD内,以E为坐标原点,以E→F为x轴正方向,E→A为y轴正方向建立平面直角
=2
坐标系,则F(,),设M(x,y),则有 (x ) 2 y2 x2 y2 ,化简得(x ) 2 y2 ,即点M在平面
30 -3 + =2 + +1 + =4
AEFD内的轨迹方程为(x ) 2 y2 ( x ,y ),所以点M在平面AEFD内的轨迹为以( ,)
+1 + =40≤ ≤1 >0 -10
为圆心,为半径的圆.易得点M在四边形AEFD内的轨迹为该圆的一段弧,弧所对的圆心角为π,所以弧
2
3
长为π 2π, 正确.要使三棱锥M BCF的体积最大,只要点M的纵坐标的绝对值最大即可.令x
×2= B =
3 3
0
,则y
=± 3
,又yM>0 ,所以M(
0
,
3
),此时M到平面EBCF的最大距离为
3
,
C
正确.三棱锥M BCF
外接球的球心在过 BCF的外接圆圆心且垂直于平面BCF的直线上.在三棱锥M BCF中,设点Q为等
△
边 BCF外接圆的圆心,设三棱锥M BCF外接球的球心为O,半径为R,设OQ a,则有R2 a2
△ = = +4=
( a) 2 ,解得a ,所以R2 ,所以三棱锥M BCF外接球的表面积S R2 . 正确.故选
3- +7 = 3 =7 =4π =28πD
.
BCD
三、填空题:本题共 小题,每小题 分,共 分.
4 5 20
. 【命题意图】本题主要考查二项式定理 考查数学运算的核心素养.
13-240 ,
【解析】由题意,得x3y2 的系数为
2 3
·
1
( )
C52 C3 -1=-240.
. 【命题意图】本题主要考查直线与圆的位置关系 考查数学运算的核心素养.
141 ,
【解析】由题意,易得圆C的圆心为C(,),半径为 ,点P(,)在圆C上.因为 APB ,所以PA
04 2 24 ∠ =90° ⊥
PB.所以线段AB为圆C的一条不过点P的直径.直线l:x (m )y m 与圆C相交于A,B两
+ +1 -7 -1=0
点,圆心C(,)在直线l上,所以 (m ) m ,解得m .检验知m 符合题意.
04 4 +1=7 +1 =1 =1
.x y 【命题意图】本题主要考查两函数图象的公切线问题 考查逻辑推理 数学运算的核心素养.
15 - =0 , 、
【解析】设曲线y f(x)上任一点的坐标为(x,y),则该点关于直线x y 的对称点为(y,x),满足y
= - =0 =
数学参考答案 第 页 共 页
3 ( 9 )
{#{QQABAYQQggAoABAAAQhCAwU6CgIQkACAAKoGQAAIIAABiRNABAA=}#}x ,则x y ,化简可得y (x ).设曲线y x 上的切点为(x,x ),曲线y (x )上
e-1 =e-1 =ln +1 =e-1 1e1-1 =ln +1
的切点为(x, (x )),又y x 的导函数为y' x,y (x )的导函数为y' 1 ,则
2 ln 2+1 =e -1 =e =ln +1 =x
+1
{
x 1 ,
e1=x
2+1
,两式整理得x
1=-
(x
2+1
)
ln
(x
2+1
),所以(x
2+1
)
-
(x
2+1
)
=
(x
2+
x (x x) (x ) (x )
e1 2- 1 =ln 2+1- e1-1
)
-1
,解得x ,所以x .所以曲线y x 与曲线y (x )的公切线的公切点为(,),则切线
1 2=0 1=0 =e-1 =ln +1 00
的斜率为 ,故与两曲线均相切的直线的方程为x y .
1 - =0
( ]
. ,27 【命题意图】本题主要考查直线与抛物线的位置关系及最值问题 考查数学运算的核心素养.
16 0 ,
16
{x y ,
ì ïïx
=-
1, ì ïïx
=
3,
( )
【解析】由题意,联立方程 4-4+3=0解得í 2 或í 2 又点A位于第二象限,所以A 1,1 ,
x2
=
y,
î
ïï
y 1 î
ïï
y 9.
-
2 4
= =
4 4
B ( 3,9 ) .设P(x,y),则 1 x 3.设直线AP的斜率为k,则k y 0- 1 4 x2 0- 1 4 x 1.所
0 0 - < 0< = = = 0-
2 4 2 2 x 1 x 1 2
0+ 0+
2 2
以直线AP的斜率k的取值范围是( ,).因为以AB为直径的圆与直线AP交于异于点A的另一点Q,
-11
( )
所以AQ BQ.当k 时,直线AP为y 1,直线BQ为x 3,此时P 1,1 ,所以 AP ,PQ
⊥ =0 = = | |=1| |=
4 2 2 4
,所以A→P·P→Q .当k 时,所以直线BQ的斜率为 1.易得直线AP的方程为kx y 1k 1 ,
1 =1 ≠0 -k - + + =0
2 4
ì ïïkx y 1k 1 ,
- + + =0
直线BQ的方程为x
+
ky
-
9
4
k
-
3
2
=0
,联立
î
í
ïï
x ky
2
9k
4
3 ,
解得点Q的横坐标是xQ=
+ - - =0
4 2
- k
(
2
k
+
2
4 k +
)
3.因为
|
AP
|= 1+
k2 ( x
0+
1 )
= 1+
k2 (k
+1
),
|
PQ
|= 1+
k2 (xQ
-
x
0
)
=
2 +1 2
(k
-1
)(k
+1
)
2,所以 AP · PQ (k )(k ) 3.令f(k) (k )(k ) 3 ,则f'(k) (k
- k2 | | | |=- -1 +1 =- -1 +1 =- 4 -
+1
)(k ) 2 ,所以当 k 1且k 时,f'(x) ;当1 k 时,f'(x) ,所以f(k)在区间( ,),
2 +1 -1< < ≠0 >0 < <1 <0 -10
2 2
( ) ( )
,1 上单调递增,在区间 1, 上单调递减,因此当k 1时,AP · PQ 取得最大值27,且f(k)
0 1 = | | | | >
2 2 2 16
( ]
,所以 AP · PQ ,27 .
0 | | | |∈ 0
16
四、解答题:本题共 小题,共 分.解答应写出文字说明、证明过程或演算步骤.
6 70
.【命题意图】本题考查正 余弦定理 二倍角公式等 考查数学运算 逻辑推理的核心素养.
17 、 , , 、
【解析】()因为 B C 2A B C,
1 cos2 +cos2 =2-2sin -2sin sin
所以 2B 2C 2A B C,
1-2sin +1-2sin =2-2sin -2sin sin
即 2A 2B 2C B C.……………………………………………………………………… 分
sin =sin +sin -sin sin 2
由正弦定理得a2 b2 c2 bc,又由余弦定理a2 b2 c2 bc A,可得 A 1. ……………… 分
= + - = + -2 cos cos = 4
2
因为A (,),所以A π. ……………………………………………………………………………… 分
∈ 0π = 5
3
( 2 )在 △ ABC中,由等面积法得S △ ABC= S △ ABD+ S △ ACD ,
数学参考答案 第 页 共 页
4 ( 9 )
{#{QQABAYQQggAoABAAAQhCAwU6CgIQkACAAKoGQAAIIAABiRNABAA=}#}即1AC·AB· A 1AB·AD· A 1AC·AD· A ,
sin = sin + sin
2 2 2 2 2
即1 3 1 AD 1 1 AD 1. ……………………………………………… 分
×3×4× = ×4× × + ×3× × 8
2 2 2 2 2 2
所以AD 123.…………………………………………………………………………………………… 分
= 10
7
.【命题意图】本题考查等比数列的通项和数列的求和 考查数学运算 逻辑推理的核心素养.
18 , 、
【解析】(
1
)因为an
+1=2
an+1 ,所以an
+1+1=2
an+1+1=2 (an+1 ).……………………………………
2
分
又因为a
1+1=2
,所以{an+1 }是首项为
2
,公比为
2
的等比数列.………………………………………
4
分
(
2
)由(
1
)易知an+1=2×2 n
-1
=2
n,an=2 n
-1
,……………………………………………………………
5
分
n n
所以 2 2 1 1 .……………………………………………………… 分
anan =(n )(n +1 )= n - n +1 7
+1 2-1 2 -1 2-1 2 -1
n k n ( )
所以Sn=k∑(k ) 2 (k +1 )=k∑ k 1 - k + 1 1 =1- n + 1 1 .………………………………… 9 分
=12-1 2 -1 =1 2-1 2 -1 2 -1
欲使不等式 log a ( 1- a) > Sn 对任意正整数n恒成立,只要 log a ( 1- a) ≥1 .…………………………… 10 分
由题意可得a ,a 且 a ,解得 a .只需 a a,解得a 1.
>0 ≠1 1- >0 0< <1 1- ≤ ≥
2
[ )
综上所述,实数a的取值范围是 1, .………………………………………………………………… 分
1 12
2
.【命题意图】本题考查离散型随机变量的分布列及数学期望 考查数学运算 逻辑推理的核心素养.
19 , 、
( )
【解析】()()比赛结束时恰好进行了 局,甲夺冠的概率为P 3 3 27,
1 i 3 1= =
5 125
( )
乙夺冠的概率为P 2 3 8 ,………………………………………………………………………… 分
2= = 2
5 125
所以比赛结束时恰好进行了 局的概率为P P P 27 8 35 7. ……………………… 分
3 = 1+ 2= + = = 3
125 125 125 25
()X的可能取值为 ,.…………………………………………………………………………………… 分
ii 23 4
( ) ( )
因为P(X ) 3 2 2 2 13,
=2= + =
5 5 25
P(X ) P(X ) 12,……………………………………………………………………………… 分
=3=1- =2= 6
25
所以X的分布列如下:
X
2 3
P 13 12
25 25
故E(X) 13 12 62.…………………………………………………………………………… 分
=2× +3× = 8
25 25 25
()因为比赛成绩Y近似地服从正态分布N(μ,σ2 ),
2
所以比赛选手可获得“参赛纪念证书”的概率:
P(μ σ Y μ σ)
- ≤ ≤ +2
1P(μ σ Y μ σ) 1P(μ σ Y μ σ)
= - ≤ ≤ + + -2≤ ≤ +2
2 2
1 . 1 . . .
≈ ×06827+ ×09545=08186
2 2
. . ,
200×08186=16372≈164
数学参考答案 第 页 共 页
5 ( 9 )
{#{QQABAYQQggAoABAAAQhCAwU6CgIQkACAAKoGQAAIIAABiRNABAA=}#}所以估计获得“参赛纪念证书”的选手人数为 .……………………………………………………… 分
164 12
.【命题意图】本题主要考查线面位置关系以及利用空间向量求二面角 考查直观想象 数学运算的核心素养.
20 , 、
【解析】()如图,连接DC.因为四边形DDCC 为菱形, DDC ,所以 DCC ,所以DC .
1 1 1 1 ∠ 1 =120° ∠ 1=60° 1=2
因为AD DC ,AC ,所以AD2 DC2 AC2 ,所以AD DC.………………………………… 分
= =2 1=22 + 1= 1 ⊥ 1 1
又AD DC,DC DC D,
⊥ ∩ 1=
所以AD 平面CDDC,所以AD DE,AD DC.……………………………………………………… 分
⊥ 1 1 ⊥ ⊥ 2
因为四边形DDCC 为菱形,且 DDC ,所以DD DC DC.
1 1 ∠ 1 =120° 1= 1= 1 1
因为E为棱CD 的中点,所以DE CD.
1 1 ⊥ 1 1
又CD CD,所以DE CD.
1 1∥ ⊥
因为DE AD,AD DC D,所以DE 平面ABCD.…………………………………………………… 分
⊥ ∩ = ⊥ 4
()以D为坐标原点,D→A,D→C,D→E分别为x轴、y轴、z轴正方向,建立如图所示的空间直角坐标系Dxyz.
2
易知DE ,所以A(,,),B(,,),C(,,),E(,, ),B(,, ),
= 3 200 220 020 00 3 1 21 3
C(,, ).
101 3
所以C→C (, , ),D→C (,,),A→E ( ,, ),D→B (,,),D→A
1= 0-1 3 = 020 = -20 3 = 220 =
(,,).
200
设C→F tCC→( t ),则D→F D→C C→F (, t,t).………………… 分
= 10≤ ≤1 = + = 02- 3 6
因为AE 平面BDF,所以存在唯一的λ,μ R,
∥ ∈
使得A→E λD→B μD→F λ(,,)μ(, t,t) (λ,λ μ tμ, μt).
= + = 220+ 02- 3 = 2 2+2 - 3
所以 λ ,λ μ tμ , μt ,解得t 2.…………………………………………………… 分
2=-22+2 - =0 3 = 3 = 7
3
æ ö
所以D→F
=è
ç
0
,4,23ø ÷,DB→
1=
(
2
,
1
,
3
).…………………………………………………………………
8
分
3 3
设平面BDF的法向量为n (x,y,z),
= 1 1 1
{ D→F·n , { 4y 23z ,
则 =0所以 1+ 1=0
3 3
D→B·n
=0
,
x y .
21+21=0
取y ,则x ,z .
1=-3 1=3 1=23
所以平面BDF的一个法向量为n (, , ). ……………………………………………………… 分
= 3-323 9
设平面ABD的法向量为m (x,y,z),
1 = 2 2 2
{ D→A·m , {x ,
则 =0 所以 22=0
DB→·m , x y z .
1 =0 22+ 2+ 32=0
取y ,则x ,z .
2=3 2=0 2=- 3
所以平面ABD的一个法向量为m (,, ).……………………………………………………… 分
1 = 03- 3 10
设平面ABD与平面BDF的夹角为θ,
1
n·m
则 θ | | 15 10.
cos =n m = =
|||| 30×23 4
故平面ABD与平面BDF夹角的余弦值为 10.……………………………………………………… 分
1 12
4
.【命题意图】本题主要考查直线与椭圆的位置关系 考查数学抽象 数学运算的核心素养.
21 , 、
数学参考答案 第 页 共 页
6 ( 9 )
{#{QQABAYQQggAoABAAAQhCAwU6CgIQkACAAKoGQAAIIAABiRNABAA=}#}【解析】()根据题意,蒙日圆的半径为 ,所以a2 b2 .
1 13 + =13
因为 PP ,所以b ,所以a ,所以椭圆E的标准方程为x2 y2 .……………………… 分
| 1 2|=2 =1 =23 + =1 1
12
( )
因为直线l 过点Q ,1 ,且易知直线l 的斜率存在,
1 0 1
2
所以可设直线l:y kx 1,A(x,y),B(x,y),
1 = + 1 1 2 2
2
ì
ï ïy
=
kx
+
1,
联立方程í 2
î
ï ïx2
y2 ,
+ =1
12
消去y并整理可得(k2 )x2 kx .
12 +1 +12 -9=0
由根与系数的关系可得,x x 12 k ,xx 9 . ……………………………………… 分
1+ 2=- k2 1 2=- k2 2
12 +1 12 +1
因为P(,),P(, ),所以直线AP:y y 1-1x ,直线BP:y y 2+1x .
101 20-1 1 = x +1 2 = x -1
1 2
y ( )
所以y y -1 =y 1 x - 1 1 = x x 2 ( ( y y 1-1 ) )= x 2 ( kx 1- 1 2)= kx 1 x 2- 1 2 x 2 = kx 1 x 2- 1 2 (x 1+ x 2 ) + 1 2 x 1 ……… 4 分
+1 2+1 1 2+1 x kx 3 kxx 3x kxx 3x
x 1 2+ 1 2+ 1 1 2+ 1
2 2 2 2
k ( k )
9 1 12 1x
- k2 - × - k2 + 1
12 +1 2 12 +1 2
= k
9 3x
- k2 + 1
12 +1 2
k
3 1x
- k2 + 1
12 +1 2 1.
= k =
9 3x 3
- k2 + 1
12 +1 2
所以y ,即直线AP,BP 的交点P在直线y 上. ………………………………………………… 分
=2 1 2 =2 6
()设直线l 与直线AP,BP 的交点分别为C(x,y),D(x,y),
2 2 1 1 3 3 4 4
则由()直线AP:y y 1-1x ,直线BP:y y 2-1x .
1 1 = x +1 1 = x +1
1 2
ì ï ïy
=
y 1
x
-1x
+1
, ì ï ïy
=
y 2
x
-1x
+1
,
联立í 1 及í 2
ï ï
î ï y 1x , î ï y 1x ,
=- +3 =- +3
2 2
x x
可得x 3=(k 4 )1 x ,x 4=(k 4 )2 x .……………………………………………………………… 7 分
2+1 1-1 2+1 2-1
因为x x (x x) 2 xx ( 12 k ) 2 36 6 16 k2 +1,
|1- 2|= 1+ 2 -41 2= - k2 + k2 = k2
12 +1 12 +1 12 +1
又点P 到直线l 的距离d |0+2×1-6| 45, …………………………………………………… 分
1 2 = = 8
5 5
所以S 1 CD ·d 25 CD ,只需求CD 的最小值.
= = | |
2 5
由弦长公式可得 | CD |= 1+ ( - 1 ) 2 | x 3- x 4|= 5 (k 4 x )1 x -(k 4 x )2 x
2 2 2+1 1-1 2+1 2-1
数学参考答案 第 页 共 页
7 ( 9 )
{#{QQABAYQQggAoABAAAQhCAwU6CgIQkACAAKoGQAAIIAABiRNABAA=}#}x x x x
=25× [(k )x 1] - [(2 k )x ] =25× (k ) 2xx 1( - k 2 )(x x) …… 10 分
2+1 1-1 2+1 2-1 2+1 1 2- 2+1 1+ 2 +1
35 16
k2
+1 .
= × k
2 3+1
令 k t,则k t -1.
3+1= =
3
所以35 × 1 k 6 k2 +1 = 5 × 16 (t - t2 1 ) 2 +9 = 5 × 25 ( t 1 - 16 ) 2 + 16×9 ≥ 5 × 12 = 65,当且
2 3+1 2 2 25 25 2 5 5
仅当1 16,即k 3时等号成立.
t= =
25 16
所以CD 的最小值为65.………………………………………………………………………………… 分
| | 11
5
所以 PCD面积的最小值为12.
△ 1
5
故直线AP,BP,l 围成的三角形面积的最小值为12.………………………………………………… 分
1 1 2 12
5
.【命题意图】本题主要考查利用导数研究函数的零点问题 不等式证明 考查逻辑推理 数学运算的核心
22 、 , 、
素养.
【解析】()设f(x) x x ,则f'(x) 1 .
1 =ln - +1 =x-1
当x 时,f'(x) ;当 x 时,f'(x) ,
>1 <0 0< <1 >0
所以f(x)的最大值为f() .所以 x x .………………………………………………………… 分
1=0 ln ≤ -1 2
所以 (ax bx )ax bx .
ln + -1≤ + -2
又 (ax bx )ax bx ,所以 (ax bx )ax bx .
ln + -1≥ + -2 ln + -1= + -2
所以ax bx ,所以m的值为 . ………………………………………………………………………… 分
+ =2 2 4
()由()知ax bx .
2 1 + =2
设g(x)ax bx .
= + -2
因为g() ,所以x 是函数g(x)的唯一零点.……………………………………………………… 分
0=0 =0 5
因为g'(x)ax a bx b,又由 a ,b ,得 a , b .
= ln + ln 0< <1 >1 ln <0ln >0
令g'(x) ,则ax a bx b ,所以 (b)x ln a .
=0 ln + ln =0 a =- b
ln
所以g'(x) 有唯一解x b
(
ln
a)
.……………………………………………………………… 分
=0 0=loga - b 6
ln
令h(x)g'(x),则h'(x)ax( a) 2 bx( b) 2.
= = ln + ln
从而对任意x R,h'(x) ,所以h(x)g'(x)是( , )上的单调递增函数.
∈ >0 = -∞ +∞
所以当x ( ,x)时,g'(x)g'(x) ;
∈ -∞ 0 < 0 =0
当x (x, )时,g'(x)g'(x) .
∈ 0 +∞ > 0 =0
所以函数g(x)在( ,x)上单调递减,在(x, )上单调递增.……………………………………… 分
-∞ 0 0 +∞ 8
下证x .
0=0
x (x )
若x ,则x 0 ,所以g 0 g() .
0<0 0< <0 < 0=0
2 2
x
又g(
log a2
)
=
aloga2
+
bloga2
-2>
aloga2
-2=0
,且函数g(x)在以 0和
log a2
为端点的闭区间上的图象不间断,
2
数学参考答案 第 页 共 页
8 ( 9 )
{#{QQABAYQQggAoABAAAQhCAwU6CgIQkACAAKoGQAAIIAABiRNABAA=}#}x
所以在 0和
log a2
之间存在g(x)的零点,记为x
1
.………………………………………………………
10
分
2
因为 0< a <1 ,所以 log a2<0 .
x
又 0 ,所以x 与“x 是函数g(x)的唯一零点”矛盾.………………………………………… 分
<0 0<0 =0 11
2
x
若x
0>0
,同理可得,在 0和
log b2
之间存在g(x)的非
0
的零点,矛盾.
2
所以x .所以 ln a ,即 a b ,所以ab .……………………………………………… 分
0=0 - b=1 ln +ln =0 =1 12
ln
数学参考答案 第 页 共 页
9 ( 9 )
{#{QQABAYQQggAoABAAAQhCAwU6CgIQkACAAKoGQAAIIAABiRNABAA=}#}