文档内容
5.1 导数的概念及意义
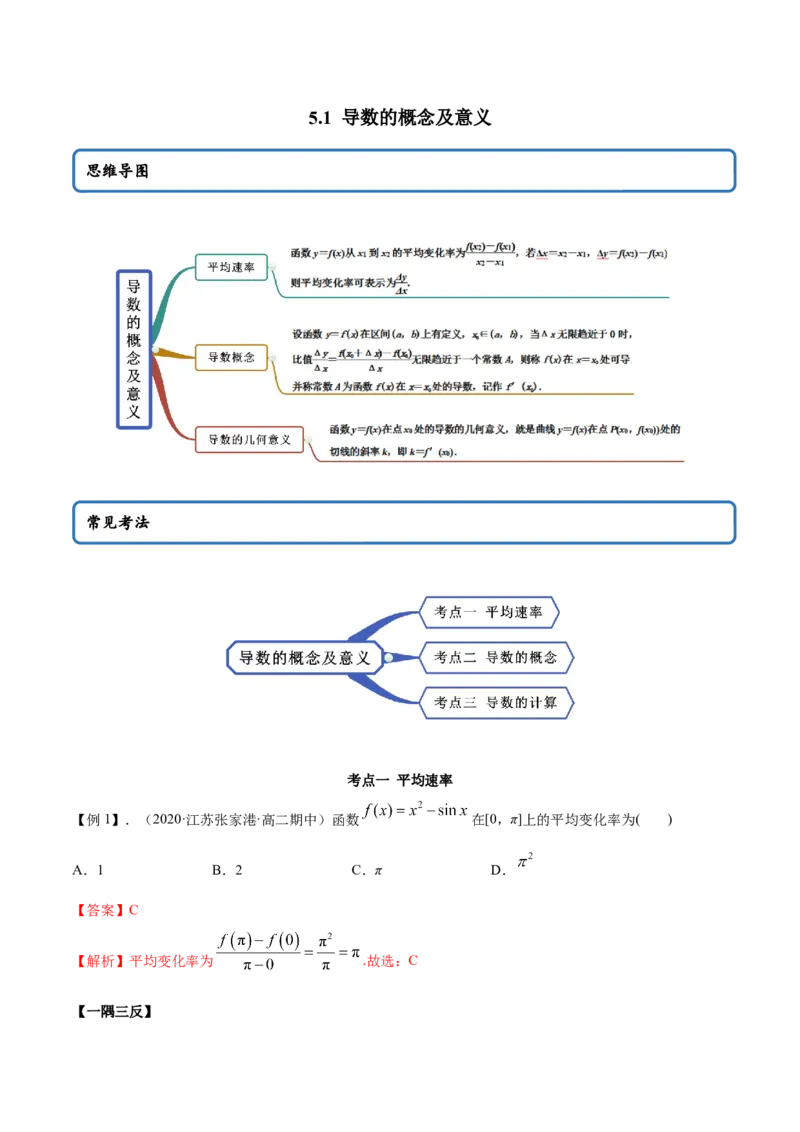
思维导图
常见考法
考点一 平均速率
【例1】.(2020·江苏张家港·高二期中)函数 在[0,π]上的平均变化率为( )
A.1 B.2 C.π D.
【答案】C
【解析】平均变化率为 .故选:C
【一隅三反】1.(2020·武汉市钢城第四中学高二期中)如果函数 在区间 上的平均变化率为 ,则
( )
A. B. C. D.
【答案】C
【解析】根据平均变化率的定义,可知 故选
2.(2020·重庆高二月考)函数 在 到 之间的平均变化率为( )
A. B. C. D.
【答案】B
【解析】 ,所以 .
故选:B
3.(2020·皇姑·辽宁实验中学高二月考)函数 在 到 之间的平均变化率为( )
A. B. C. D.
【答案】C
【解析】当 时, ;当 时, ;
所以函数 在 到 之间的平均变化率为 .故选:C.
考点二 导数的概念
【例2】(1)(2020·利辛县阚疃金石中学高三月考)设 为可导函数,且满足条件,则曲线 在点 处的切线的斜率为( )
A.10 B.3 C.6 D.8
(2).(2020·广东南海·高二期末)在高台跳水运动中 时运动员相对于水面的高度(单位: )是
,则高台跳水运动中运动员在 时的瞬时速度是( )
A. B. C.13.1 D.3.3
【答案】(1)A(2)B
【解析】因为 ,所以 ,
即 ,
因此曲线 在点 处的切线的斜率为 .故选:A.
(2)由 ,得 ,
当 时, ,
所以高台跳水运动中运动员在 时的瞬时速度 ,故选:B
【一隅三反】
1.(2020·扶风县法门高中高二月考(理))一个物体的位移s关于时间t的运动方程为s=1-t+t2,其中s
的单位是:m,t的单位是:s,那么物体在t=3 s时的瞬时速度是
A.5 m/s B.6 m/s C.7 m/s D.8 m/s
【答案】 A
【解析】由题意,位移 关于时间 的运动方程为 ,则 ,
当 时, ,故选A.
2.(2020·赣州市赣县第三中学高二月考(文))已知函数f(x)在x=x 处的导数为12,则
0( )
A.-4 B.4 C.-36 D.36
【答案】A
【解析】根据题意,函数 在 处的导数为12,
则 ;故选:A.
3.(2020·赣州市赣县第三中学高二月考(理))已知函数 ,则
( )
A.1 B.-1 C. D.
【答案】B
【解析】 , ,
,
∴ .故选:B
4.(2020·广东佛山·高二期末)若 ,则 ( )
A. B. C. D.
【答案】A【解析】根据题意, ,故选:A.
考点三 导数的计算
【例3】(2020·河南)设点P是函数 图象上的任意一点,点P处切线的倾斜
角为 ,则角 的取值范围是( )
A. B.
C. D.
【答案】B
【解析】 ,
, , , ,
.
点P是曲线上的任意一点,点P处切线的倾斜角为 , .
, .
故选:B.
【一隅三反】
1.(2020·河南商丘)函数 的图象在点 处的切线的倾斜角为 ,则 (
)
A. B. C. D.
【答案】B
【解析】由题意得 ,所以切线斜率 ,所以 .故选:B.
2.(2020·云南)已知函数 ,则函数 的图象在点 处的切线斜率
为( )
A. B. C. D.
【答案】C
【解析】∵ ,∴ ,∴ ,解得
,∴ ,因此,函数 的图象在点 处的切线斜率为
故选C
3.(2020·云南高三月考(理))已知函数 ,则函数 的图象在点
处的切线斜率为( )
A. B. C. D.
【答案】C
【解析】∵ ,∴ ,∴ ,解得
,∴ ,因此,函数 的图象在点 处的切线斜率为
故选C