文档内容
5.2.3简单复合函数的导数 -B提高练
一、选择题
1.(2021·广东揭阳市高二期末)函数 的导函数 为( )
A. B.
C. D.
【答案】B
【详解】函数 可以看作函数 和 的复合函数,根据复合
函数的求导法则有 .故选:B.
2.(2020·四川省眉山车城中学高二期中)已知函数 ,则 (
)
A.1 B.-1 C.2 D.3
【答案】B
【详解】因为 ,所以 ,
令 ,可得 ,解得 .故选:B.
3.(2021·江苏徐州市·高三期末)随着科学技术的发展,放射性同位素技术已经广泛应用于医学、
航天等众多领域,并取得了显著经济效益.假设某放射性同位素的衰变过程中,其含量 (单位:
贝克)与时间 (单位:天)满足函数关系 ,其中 为时该放射性同位素的含量.已
知 时,该放射性同位素的瞬时变化率为 ,则该放射性同位素含量为 贝克时衰变所需时间为( )
A.20天 B.30天 C.45天 D.60天
【答案】D
【详解】由 得 ,因为 时,该放射性同位素的瞬时变
化率为 ,即 ,解得 ,
则 ,当该放射性同位素含量为 贝克时,即 ,
所以 ,即 ,所以 ,解得 .故选:D.
4.已知直线y=x+1与曲线y=ln(x+a)相切,则a的值为( )
A.1 B.2 C.-1 D.-2
【答案】B
【详解】设切点坐标是(x,x+1),依题意有
0 0
由此得x+1=0,x=-1,a=2.
0 0
5.(多选题)(2021·江苏高二)以下函数求导正确的是( )
A.若 ,则
B.若 ,则
C.若 ,则
D.若 ,则
【答案】AC
【详解】对A, ,故A正确
对B, ,故B错;对C,所以C正确对D, ,故D错;故选:AC
6.(多选题)(2021·全国高二课时练)已知函数 及其导数 ,若存在 ,使得
,则称 是 的一个“巧值点”.下列函数中,有“巧值点”的是( )
A. B. C. D.
【答案】ACD
【详解】在A中,若 ,则 ,则 ,这个方程显然有解,故A符合要求;
在B中,若 ,则 ,即 ,此方程无解,故
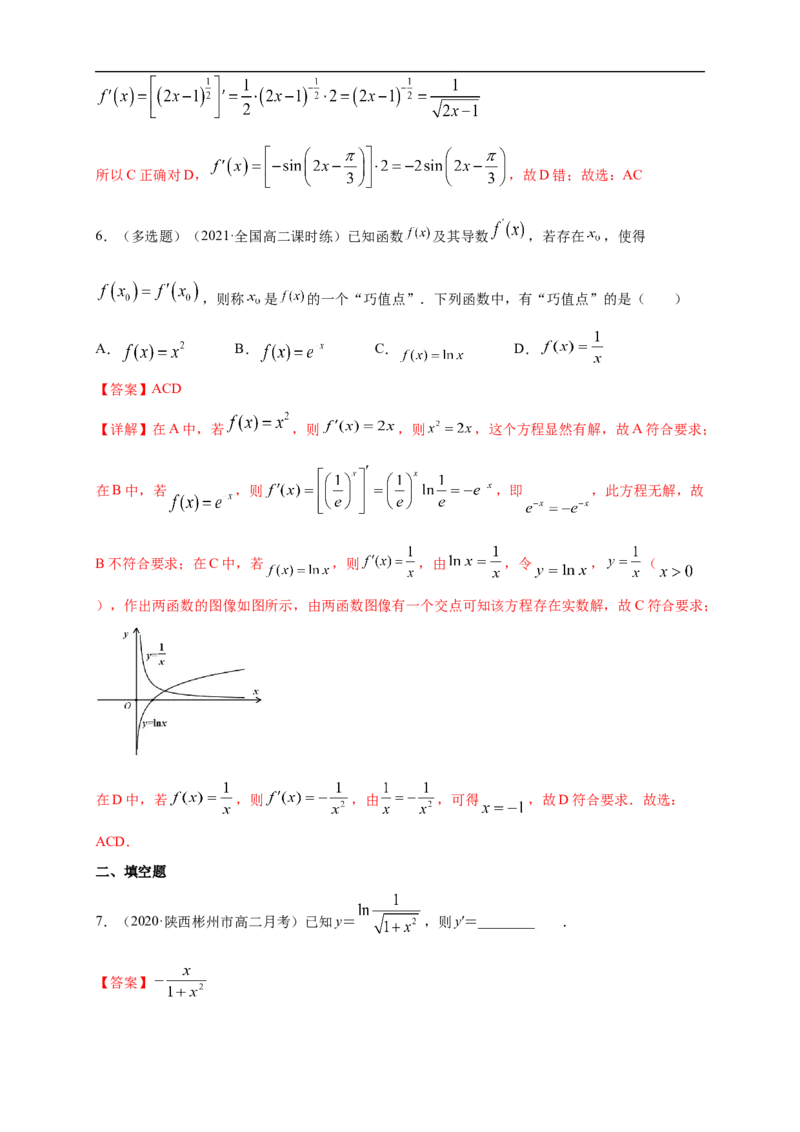
B不符合要求;在C中,若 ,则 ,由 ,令 , (
),作出两函数的图像如图所示,由两函数图像有一个交点可知该方程存在实数解,故C符合要求;
在D中,若 ,则 ,由 ,可得 ,故D符合要求.故选:
ACD.
二、填空题
7.(2020·陕西彬州市高二月考)已知y= ,则y′=________ .
【答案】【详解】y= = =- ln(1+x2),所以y′=- ·(2x)= .
8.(2020·洛阳市第一高级中学高二月考)函数 的图像在点 处的切线的
斜率为_________.
【答案】
【详解】因为函数 ,所以 ,则在点 处的切线的斜率
.
9.(2020·广东湛江市·湛江二十一中高二开学考试)若函数 , ,
则 __________.
【答案】3
【详解】由 ,得 ,
, , 。
10.(2020·广东中山市)在许多实际问题中,一个因变量往往与几个自变量有关,即因变量的值
依赖于几个自变量,这样的函数称为多元函数.例如,某种商品的市场需求量不仅仅与其市场价格
有关,而且与消费者的收入以及这种商品的其他代用品的价格等因素有关,即决定该商品需求量的
因素不止一个而是多个.我们常常用偏导数来研究多元函数.以下是计算二元函数
在 处偏导数的全过程:
, ,所以 ,
,由上述过程,二元函数 ,则
______.
【答案】【详解】根据题意,得到 , ,
则 , ,因此 .
三、解答题
11.设函数f (x)=aexln x+.
(1)求导函数f ′(x);
(2)若曲线y=f (x)在点(1,f (1))处的切线方程为y=e(x-1)+2,求a,b的值.
【详解】(1)由f (x)=aexln x+,
得f ′(x)=(aexln x)′+=aexln x++.
(2)由于切点既在曲线y=f (x)上,又在切线y=e(x-1)+2上,
将x=1代入切线方程得y=2,将x=1代入函数f (x)得f (1)=b,
∴b=2.将x=1代入导函数f ′(x)中,
得f ′(1)=ae=e,∴a=1.
12.(2020·江苏高二专题练习)已知函数 ,记 为 的导数,
.
(1)求 ;
(2)猜想 的表达式,并证明你的猜想.
【详解】解:(1)因为 ,则 , ,
(2)猜想: .
下面用数学归纳法证明:
①当 时, ,结论成立;
②假设 ( 且 )时,结论成立,即 .
当 时,.
所以当 时,结论成立.
所以由①②可知对任意的 结论成立.