文档内容
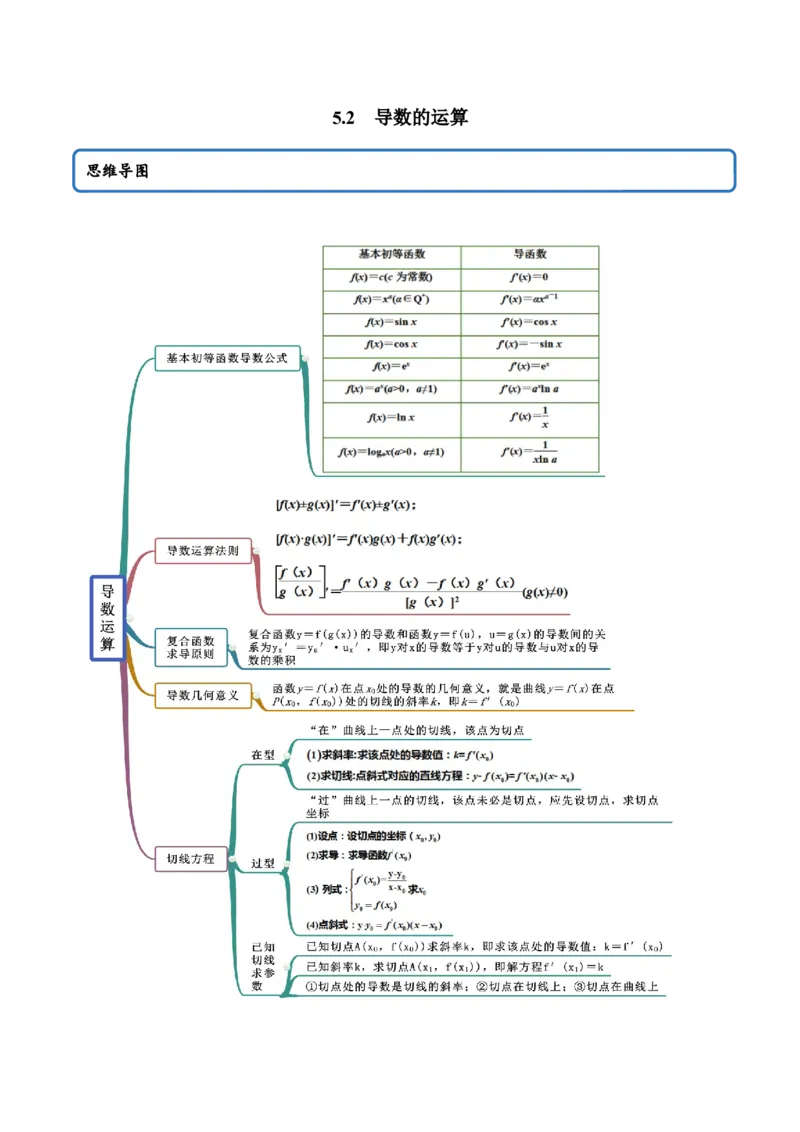
5.2 导数的运算
思维导图常见考法
考点一 初等函数求导
【例1】(2020·林芝市第二高级中学高二期末(文))求下列函数的导函数.
(1)
(2)
(3)
(4)
(5)
(6)
【答案】(1) (2) (3) (4)
(5) (6)【解析】(1)由 ,则 ;
(2)由 ,则 ;
(3)由 ,则 ;
(4)由 ,则 ;
(5)由 ,则 ;
(6)由 ,则 .
【一隅三反】
1.(2020·西藏高二期末(文))求下列函数的导数.
(1) ;
(2) ;
(3) .
【答案】(1) (2) (3)
【解析】(1)
(2)
(3)
2.(2020·通榆县第一中学校高二月考(理))求下列函数的导数:
(Ⅰ) ;(Ⅱ) .
【答案】(Ⅰ) ;(Ⅱ) .
【解析】(Ⅰ)由导数的计算公式,可得 .
(Ⅱ)由导数的乘法法则,可得 .
3.(2020·山东师范大学附中高二期中)求下列函数在指定点的导数:
(1) , ;
(2) , .
【答案】(1) (2)
【解析】(1) ,
(2) ,
考点二 复合函数求导
【例2】.(2020·凤阳县第二中学高二期末(理))求下列函数的导数:
(1) ;(2) .
【答案】(1) ;(2) 或 .
【解析】(1) ;
(2) .或 .
【一隅三反】1.(2020·陕西碑林·西北工业大学附属中学高二月考(理))求下列函数的导数:
(1) ;
(2) ;
(3) ;
(4) .
【答案】(1) ;(2) ;
(3) ;(4) .
【解析】(1) ;
(2) ;
(3)∵ ∴ ;
(4) .
2.(2020·横峰中学高二开学考试(文))求下列各函数的导数:
(1) ;(2) (3)y=
【答案】(1) ;(2) .(3)
【解析】(1)因为 令 ,
所以(2) .
(3)令 ,则 ,
所以 ;
考点三 求导数值
【例3】.(2020·甘肃城关·兰州一中高二期中(理))已知函数 的导函数为 ,且满足
,则
A. B. C. D.
【答案】A
【解析】 ,求导得 ,则 ,解得 .
故选:A.
【一隅三反】
1.(2020·广东湛江·高二期末(文))已知函数 ,则 ( )
A. B. C. D.
【答案】A
【解析】 , ,因此, .
故选:A.2.(2020·四川高二期中(理))若函数 ,则 的值为( )
A.0 B. C. D.
【答案】B
【解析】因为 ,所以令 ,则 ,
所以 ,则 ,故选: B.
3.(2020·广西桂林·高二期末(文))已知函数 ,则 ( )
A.3 B.0 C.2 D.1
【答案】A
【解析】由题得 .故选:A
考点四 求切线方程
【例4】.(2020·郸城县实验高中高二月考(理))已知曲线
(1)求曲线在点 处的切线方程;
(2)求曲线过点 的切线方程
【答案】(1) ;(2) 或 .
【解析】(1)∵ ,∴在点 处的切线的斜率 ,
∴曲线在点 处的切线方程为 ,即 .
(2)设曲线 与过点 的切线相切于点 ,
则切线的斜率 ,∴切线方程为 ,即 .
∵点 在该切线上,∴ ,即 ,
∴ ,∴ ,
∴ ,解得 或 .
故所求切线方程为 或 .
【一隅三反】
1.(2020·黑龙江大庆实验中学高三月考(文))曲线 在点 处的切线方程为
A. B. C. D.
【答案】A
【解析】 的导数为 ,
可得曲线 在点 处的切线斜率为 ,
所以曲线 在点 处的切线方程为 ,即 ,故选A.
2.(2020·河南高三其他(理))曲线 在某点处的切线的斜率为 ,则该切线的方程
为( )
A. B.
C. D.
【答案】D【解析】求导得 ,根据题意得 ,解得 (舍去)或 ,可得切点的坐
标为 ,所以该切线的方程为 ,整理得 .故选:D.
3.(2020·北京高二期末)过点P(0,2)作曲线y= 的切线,则切点坐标为( )
A.(1,1) B.(2, ) C.(3, ) D.(0,1)
【答案】A
【解析】设切点 , ,即切点
故选:A
4.(2020·吉林洮北·白城一中高二月考(理))已知函数f(x)=x3-4x2+5x-4.
(1)求曲线f(x)在点(2,f(2))处的切线方程;
(2)求经过点A(2,-2)的曲线f(x)的切线方程.
【答案】(1)x-y-4=0
(2)x-y-4=0或y+2=0
【解析】(1)∵f′(x)=3x2-8x+5,
∴f′(2)=1,又f(2)=-2,
∴曲线f(x)在点(2,f(2))处的切线方程为y-(-2)=x-2,即x-y-4=0.
(2)设切点坐标为(x,x3-4x2+5x-4),
0 0 0 0
∵f′(x )=3x2-8x+5,
0 0 0
∴切线方程为y-(-2)=(3x2-8x+5)(x-2),
0 0
又切线过点(x,x3-4x2+5x-4),
0 0 0 0
∴x3-4x2+5x-2=(3x2-8x+5)(x-2),
0 0 0 0 0 0
整理得(x-2)2(x-1)=0,解得x=2或x=1,
0 0 0 0
∴经过A(2,-2)的曲线f(x)的切线方程为x-y-4=0或y+2=0.考点五 利用切线求参数
【例5】.(2020·全国高三其他(理))已知曲线 在点 处的切线方程为 ,
则 ( )
A. B.0 C.1 D.
【答案】D
【解析】令 ,则 ,
所以 ,
因为曲线 在点 处的切线方程为 ,
所以该切线过原点,
所以 ,解得 ,
即 .
故选:D.
【一隅三反】
1.(2020·岳麓·湖南师大附中月考)已知函数 ,若曲线 在 处的切线
与直线 平行,则 ______.
【答案】
【解析】因为函数 ,所以 ,
又因为曲线 在 处的切线与直线 平行,所以 ,解得 ,故答案为:
2.(2020·安徽庐阳·合肥一中高三月考(文))曲线 在点(0,1)处的切线的斜率为2,则
a=_____.
【答案】1
【解析】 , , .
故答案为:1.
3.(2020·山东莱州一中高二月考)已知直线 是曲线 的一条切线,则 ________.
【答案】4
【解析】设 ,切点为 ,
因为 ,
所以 ,解得 ,
所以 ,
故切点为 ,又切点在切线 上,
故 .
故答案为:4