中学生标准学术能力诊断性测试2024届高三下学期3月测试数学试卷_2024年3月_013月合集_2024届中学生标准学术能力诊断性测试高三3月联考_2024届中学生标准学术能力诊断性测试高三3月-数学

中学生标准学术能力诊断性测试 2024 年 3 月测试 6． 已知圆 数学试卷 本试卷共 150分，考试时间 120分钟。 一、单项选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是 符合题目要求的． 1． 已知集合A=  2a2,a−4,−10  ,B=−a+10,−2−4a,25 ，且A B=−10 ，则 A．A=8,−2,−10 B．B=−10,−78,25 C．a=2或20 D．A B=800,16,−10,−82,25 x2 −3x,x3 2． 已知函数 f (x)= ，若x R，使得 f (x )10m+4m2 成立，则实数m的 log x,x>3 0 0  3 取值范围为  9 1  5  A． − ,− B． − ,0      4 4  2   9  1   5 C． −,−   − ,+  D． −,−  0,+)  4  4   2 2  1 31  3． 已知sin  +  = ，那么tan  −  =  7  5  14  1 2 6 A．− B．2 6 C． D．2 6 5 5 1 1 1 4． 已知数列 a  的前n项和为S ，且S =n2 +3n，若首项为 的数列 b  满足 − =a ， n n n 2 n b b n n+1 n 则数列 b  的前2024项和为 n 1012 2025 2023 2024 A． B． C． D． 2023 2024 2024 2025 7  5． 已知点A(2,6),B(−2,−3),C(0,1),D  ,6 ，则与向量AB+2CD同方向的单位向量为 2  3 10 10   10 3 10  2 5 5  4 3 A．  ,   B．  ,   C．  ,−   D． − ,   10 10   10 10   5 5   5 5 第1页 共4页 第2页 共4页 M : x 2 + y 2 − 2 a x = 0 ( a > 0 ) 的圆心到直线 2 x + y = 2 距离是 5 ，则圆 M 与圆 N : ( x − 2 ) 2 + ( y + 1 ) 2 = 1 的位置关系是 A．外离 B．相交 C．内含 D．内切 7． 已知  3 x 2 + 1 x  n 的展开式的各项系数和为4096，则展开式中 x 6 的系数为 A．15 B．1215 C．2430 D．81 8． 设 a  R ，若复数 2 a + − 3 2 i i （ i 为虚数单位）在复平面内对应的点在直线 y = − x 上，则 a = A． − 2 B． − 1 0 C． 2 5 D． 2 二、多项选择题：本题共4小题，每小题5分，共20分．在每小题给出的四个选项中，有多项符合 题目要求．全部选对得5分，部分选对但不全得2分，有错选的得0分. 9． 下列说法正确的是  1  A．不等式4x2−5x+1>0的解集是x x> 或x<1  4   3  B．不等式2x2−x−60的解集是x x− 或x2  2  C．若不等式ax2+8ax+21<0恒成立，则a的取值范围是 1 D．若关于x的不等式2x2 + px−3<0的解集是 (q,1) ，则 p+q的值为− 2 10．已知m、n为两条不重合的直线，、为两个不重合的平面，则下列说法正确的是 A．若m⊥,n⊥且 ，则m n B．若m⊥n,m⊥,n⊥，则⊥ C．若m n,n, ，则m  D．若m n,n⊥,⊥,m，则m  x2 y2 11．设椭圆C: + =1的左、右焦点分别为F、F ,P是C上的动点，则下列结论正确的是 1 2 25 16 A． PF + PF =5 1 2 3 B．离心率e= 5 C．PFF 面积的最大值为12 1 2 D．以线段FF 为直径的圆与圆(x−4)2 +(y−3)2 =4相切 1 2 {#{QQABbYAEggCAQBIAAQhCAwGYCAGQkACCCKoOABAEsAAAyRNABCA=}#}kx−k,x1 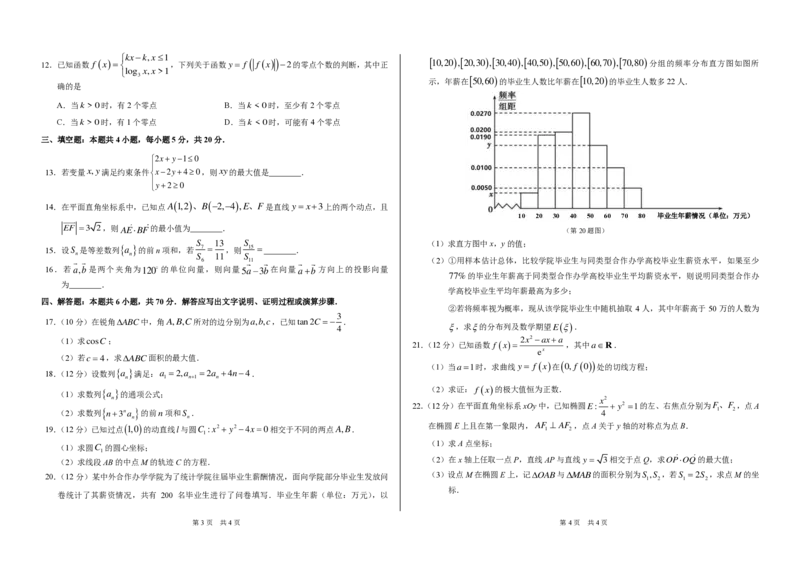12．已知函数 f (x)= ，下列关于函数y= f ( f (x)) −2的零点个数的判断，其中正 10,20),20,30),30,40),40,50),50,60),60,70),70,80) 分组的频率分布直方图如图所 log x,x>1  3 示，年薪在 50,60) 的毕业生人数比年薪在 10,20) 的毕业生人数多22人． 确的是 A．当k >0时，有2个零点 B．当k <0时，至少有2个零点 C．当k >0时，有1个零点 D．当k <0时，可能有4个零点 三、填空题：本题共4小题，每小题5分，共20分． 2x+ y−10  13．若变量x,y满足约束条件x−2y+40，则xy的最大值是 ．  y+20  14．在平面直角坐标系中，已知点A(1,2)、B(−2,−4),E、F是直线y=x+3上的两个动点，且 10 20 30 40 50 60 70 80 毕业生年薪情况（单位：万元） EF =3 2，则AEBF的最小值为 ． （第20题图） S 13 S （1）求直方图中x，y的值； 15．设S 是等差数列 a  的前n项和，若 7 = ，则 15 = ． n n S 11 S 6 11 （2）①用样本估计总体，比较学院毕业生与同类型合作办学高校毕业生薪资水平，如果至少 16．若a,b 是两个夹角为120 的单位向量，则向量5a−3b在向量a+b 方向上的投影向量 77%的毕业生年薪高于同类型合作办学高校毕业生平均薪资水平，则说明同类型合作办 为 ． 学高校毕业生平均年薪最高为多少； 四、解答题：本题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤． ②若将频率视为概率，现从该学院毕业生中随机抽取 4 人，其中年薪高于 50 万的人数为 3 17．（10分）在锐角ABC中，角A,B,C所对的边分别为a,b,c，已知tan2C =− ． 4 ，求的分布列及数学期望E()． （1）求cosC； 21．（12分）已知函数 f (x)= 2x2 −ax+a ，其中aR． ex （2）若c=4，求ABC面积的最大值． （1）当a=1时，求曲线y= f (x) 在 ( 0, f (0)) 处的切线方程； 18．（12分）设数列 a  满足：a =2,a =2a +4n−4． n 1 n+1 n （1）求数列 a  的通项公式； （2）求证： f (x)的极大值恒为正数． n x2 22．（12分）在平面直角坐标系xOy中，已知椭圆E: + y2 =1的左、右焦点分别为F、F ，点A （2）求数列  n+3na  的前n项和S ． 4 1 2 n n 19．（12分）已知过点 (1,0) 的动直线l与圆C :x2 + y2 −4x=0相交于不同的两点A,B． 在椭圆E上且在第一象限内，AF 1 ⊥ AF 2 ，点A关于y轴的对称点为点B． 1 （1）求A点坐标； （1）求圆C 的圆心坐标； 1 （2）求线段AB的中点M的轨迹C的方程． （2）在x轴上任取一点P，直线AP与直线y = 3相交于点Q，求OPOQ的最大值； 20．（12 分）某中外合作办学学院为了统计学院往届毕业生薪酬情况，面向学院部分毕业生发放问 （3）设点M在椭圆E上，记OAB与MAB的面积分别为S ,S ，若S =2S ，求点M的坐 1 2 1 2 标． 卷统计了其薪资情况，共有 200 名毕业生进行了问卷填写．毕业生年薪（单位：万元），以 第3页 共4页 第4页 共4页 {#{QQABbYAEggCAQBIAAQhCAwGYCAGQkACCCKoOABAEsAAAyRNABCA=}#}