文档内容
专题 05
考点1:竖直平面内圆周运动的两种模型
1.模型建立
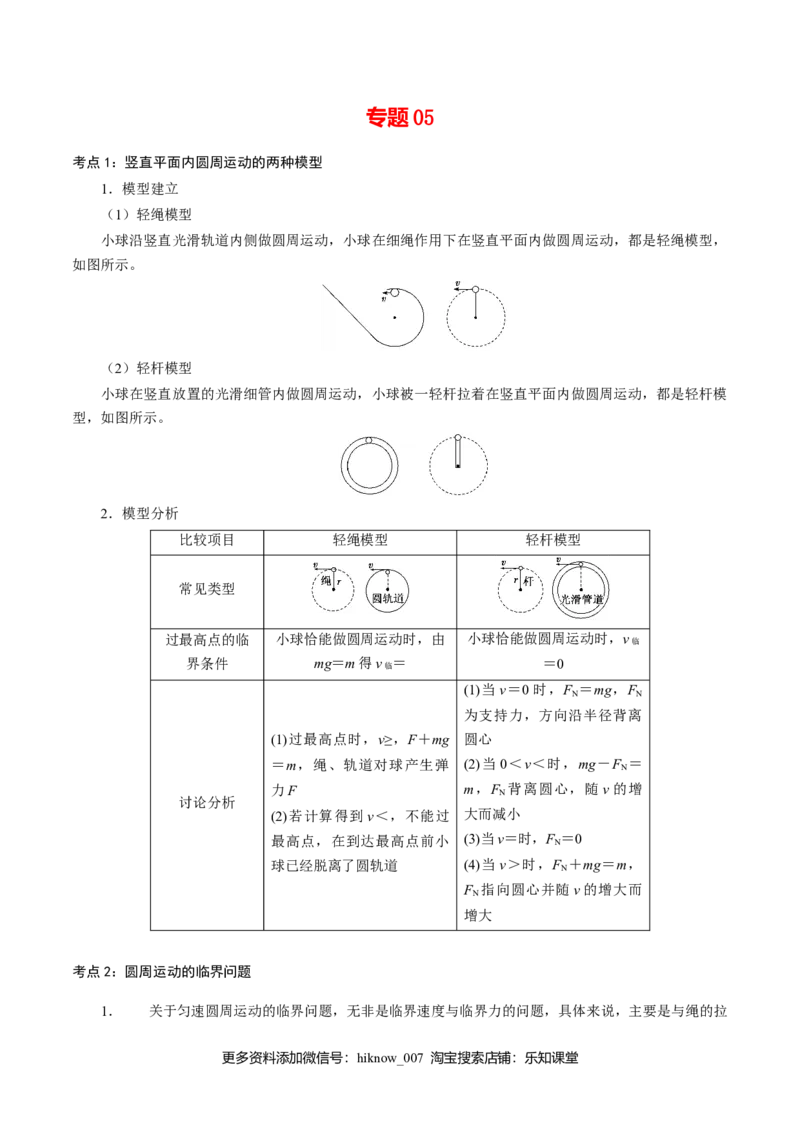
(1)轻绳模型
小球沿竖直光滑轨道内侧做圆周运动,小球在细绳作用下在竖直平面内做圆周运动,都是轻绳模型,
如图所示。
(2)轻杆模型
小球在竖直放置的光滑细管内做圆周运动,小球被一轻杆拉着在竖直平面内做圆周运动,都是轻杆模
型,如图所示。
2.模型分析
比较项目 轻绳模型 轻杆模型
常见类型
过最高点的临 小球恰能做圆周运动时,由 小球恰能做圆周运动时,v
临
界条件 mg=m得v = =0
临
(1)当v=0时,F =mg,F
N N
为支持力,方向沿半径背离
(1)过最高点时,v≥,F+mg 圆心
=m,绳、轨道对球产生弹 (2)当 0<v<时,mg-F =
N
力F m,F 背离圆心,随 v的增
N
讨论分析
(2)若计算得到v<,不能过 大而减小
最高点,在到达最高点前小 (3)当v=时,F =0
N
球已经脱离了圆轨道 (4)当v>时,F +mg=m,
N
F 指向圆心并随v的增大而
N
增大
考点2:圆周运动的临界问题
1. 关于匀速圆周运动的临界问题,无非是临界速度与临界力的问题,具体来说,主要是与绳的拉
更多资料添加微信号:hiknow_007 淘宝搜索店铺:乐知课堂力、弹簧的拉力、接触面的弹力和摩擦力等相关。在这类问题中,要特别注意分析物体做圆周运动的向心
力来源,考虑达到临界条件时物体所处的状态,即临界速度、临界角速度,然后分析该状态下物体的受力
特点,结合圆周运动知识,列方程求解。常见情况有以下几种:
(1)与绳的弹力有关的圆周运动临界问题。
(2)因静摩擦力存在最值而产生的圆周运动临界问题。
(3)受弹簧等约束的匀速圆周运动临界问题。
(4)与斜面有关的圆周运动临界问题。
2.三类常见的临界条件
(1)接触与脱离的临界条件:弹力F =0。
N
(2)相对滑动的临界条件:两物体相接触且处于相对静止时,常存在着静摩擦力,则相对滑动的临
界条件是静摩擦力达到最大值。
(3)绳子断裂与松弛的临界条件:绳子所能承受的张力是有限度的,绳子断与不断的临界条件是绳
中张力等于它所能承受的最大张力,绳子松弛的临界条件是F =0。
T
更多资料添加微信号:hiknow_007 淘宝搜索店铺:乐知课堂