文档内容
专题 3.1 函数概念及其表示
【知识储备】
1.函数的概念
一般地,设A,B是非空的数集,如果按照某种确定的对应关系f,使对于集合A中的
任意一个数x在集合B中都有唯一确定的数f(x)和它对应,那么就称f:A→B为从集合
A到集合B的一个函数,记作y=f(x),x∈A.
2.函数的定义域、值域
(1)在函数y=f(x),x∈A中,x叫做自变量,x的取值范围A叫做函数的定义域;与x的
值相对应的y值叫做函数值,函数值的集合 { f ( x ) | x ∈ A } 叫做函数的值域.
(2)如果两个函数的定义域相同,并且对应关系完全一致,我们就称这两个函数相等.
3.函数的表示法
表示函数的常用方法有解析法、图象法和列表法.
4.分段函数
(1)若函数在其定义域的不同子集上,因对应关系不同而分别用几个不同的式子来表示,
这种函数称为分段函数.
(2)分段函数虽由几个部分组成,但它表示的是一个函数.分段函数的定义域等于各段
函数的定义域的并集,值域等于各段函数的值域的并集.
必备技巧 函数的概念
(1)函数的定义要求第一个非空数集A中的任何一个元素在第二个非空数集B中有且只
有一个元素与之对应,即可以“多对一”,不能“一对多”,而B中有可能存在与A
中元素不对应的元素.
(2)构成函数的三要素中,定义域和对应关系相同,则值域一定相同.同一函数只需判
断定义域和对应关系即可.
一、单选题
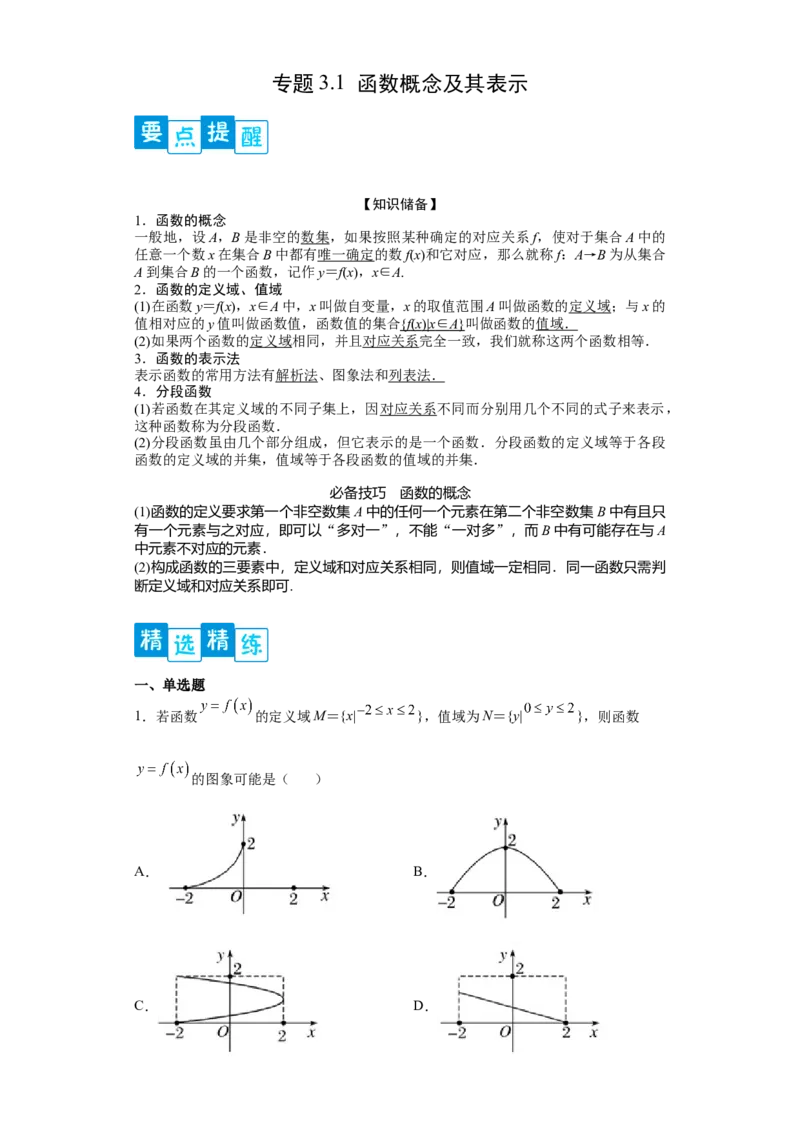
1.若函数 的定义域M={x| },值域为N={y| },则函数
的图象可能是( )
A. B.
C. D.【答案】B
【解析】A中定义域是{x|-2≤x≤0},不是M={x|-2≤x≤2},故错误;
C中图象不表示函数关系,因为存在一个 对应两个 ,不满足函数定义;
D中值域不是N={y|0≤y≤2}.
只有 中的定义域和值域满足题意,且表示函数关系,符合题意.故选:B.
2.设 ,给出下列四个图形,如下图所示,其中能
表示从集合 到 的函数关系的有( )个
A.1个 B.2个 C.3个 D.4个
【答案】A
【解析】由函数的定义知,①不能表示集合 到 的函数关系,因为图中y的范围是
[0,2];②不能表示集合 到 的函数关系,因为图中y的范围是[0,2];
③不能表示集合 到 的函数关系,因为对于一个x,可能有两个y值与之对应;
④能表示集合 到 的函数关系.
故满足题意的有④,共1个.
故选:A.
3.函数 + 的定义域为( )
A. B.(-∞,3)∪(3,+∞)
C. (3,+∞) D.(3,+∞)
【来源】黑龙江省绥化市第一中学2020-2021学年高一上学期期中考试数学试题
【答案】C
【解析】要使函数 + 有意义,则
所以 ,解得 且 ,所以函数 + 的定义域为 ∪(3,+∞).故选:C.
4.下列各组函数中,表示同一函数的是( )
A. 与 B. 与
C. 与 D. 与
【答案】B
【解析】A中, 的定义域为 , 的定义域为R,故A错误;
B中, ,B正确;
C中, 的定义域为R, 的定义域为 ,故C错误;
D中, 的定义域为 ,由 可得 的定义域为
,D错误.
故选:B
5.已知函数 与x的值对应如下表,
x 1 2 3 4 5 6
1
5 10 20 25 30
5
那么函数 的定义域为( )
A. B. C. D.
【来源】广西普通高中2021-2022学年高二6月学业水平考试 数学试题
【答案】A
【解析】由题意知:函数 的定义域为 .
故选:A.
6.下列关于函数与区间的说法正确的是( )
A.函数定义域必不是空集,但值域可以是空集B.函数定义域和值域确定后,其对应法则也就确定了
C.数集都能用区间表示
D.函数中一个函数值可以有多个自变量值与之对应
【答案】D
【解析】对于A,函数的定义域和值域均为非空数集,A错误;
对于B,若函数的定义域和值域均为 ,对应法则可以是 ,也可以是 ,B
错误;对于C,自然数集无法用区间表示,C错误;
对于D,由函数定义可知,一个函数值可以有多个自变量值与之对应,D正确.
故选:D.
7.已知函数 ,则 的值是( ).
A. B.0 C.1 D.20
【来源】广西十八校2021-2022学年高一10月联考数学试题
【答案】B
【解析】 ,
则
故选:B
8.已知函数 ,则 等于( )
A. B. C. D.0
【来源】安徽省皖北县中联盟2021-2022学年高一上学期12月联考数学试题
【答案】D
【解析】由题意,函数 ,令 ,解得 ,
令 ,可得 .
故选:D.
9.已知函数 ,其中 是x的正比例函数, 是x的反比例函数,
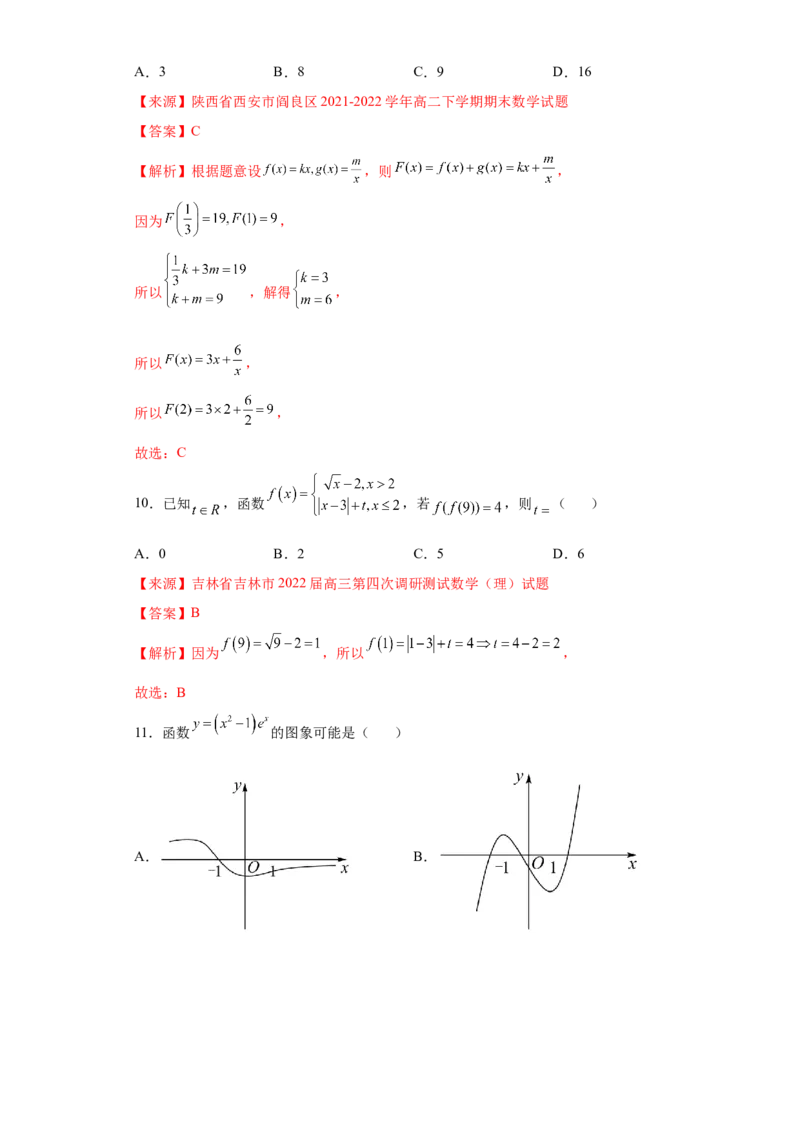
且 ,则 ( )A.3 B.8 C.9 D.16
【来源】陕西省西安市阎良区2021-2022学年高二下学期期末数学试题
【答案】C
【解析】根据题意设 ,则 ,
因为 ,
所以 ,解得 ,
所以 ,
所以 ,
故选:C
10.已知 ,函数 ,若 ,则 ( )
A.0 B.2 C.5 D.6
【来源】吉林省吉林市2022届高三第四次调研测试数学(理)试题
【答案】B
【解析】因为 ,所以 ,
故选:B
11.函数 的图象可能是( )
A. B.C. D.
【来源】专题06 函数的图像(讲义)-2023年高考数学一轮复习精讲精练宝典(新高
考专用)
【答案】C由题意,函数 ,
因为 ,即函数 的图象过点 ,可排除A、B项;
又因为 ,可排除D项,
故选:C.
12.设函数 ,则 的值为( )
A. B. C. D.18
【答案】B
【解析】 ,故选:B
13.某高中生周末自主学习时,进行了一次数学探究活动,他将一天的日期与星期用
有序数对表示,比如某个月10日,11日是周末,就分别用 和 表示,然后
在平面直角坐标系内描出对应的点.他查阅了某年七月份的日历,利用数学软件在平面
直角坐标系内描出了31个点,经过思考,他构造了函数 ,使得这些点都在 的
图象上,若 ,则下列叙述正确的是( )
A.该月12日是星期二,有五天是星期二 B.该月12日是星期一,有四天是星期
二
C.该月23日是星期六,有五天是星期六 D.该月23日是星期二,有四天是星期
二【来源】安徽省阜阳市2021-2022学年高三上学期期末教学质量统测文科数学试题
【答案】C
【解析】由题意及 可知,7月4日是星期一,列表如下:
星期一 星期二 星期三 星期四 星期五 星期六 星期日
1 2 3
4 5 6 7 8 9 10
11 12 13 14 15 16 17
18 19 20 21 22 23 24
25 26 27 28 29 30 31
可知选项C正确.
故选:C.
{x2+2x,x≤0
14.设函数f (x)= ,若 ,则实数a的值为
−x2,x>0
( )
A. B. C. D.
【答案】B
【解析】令 , ,则
1° 时, ,则 无解.
2° 时, ,∴ ,∴
时, ,则 ; 时, 无解
综上: .
故选:B.
15.已知函数 ,若 ,则
( )A. B. C. D.
【答案】A
【解析】因为函数 ,且 ,
当 时, ,即 ,
解得 或 ,
当 时, ,无解,
综上: ,
所以 ,
故选:A
16.设函数 ,若 是函数 的最小值,则实数a的取
值范围是( )
A.[﹣1,2] B. C. D.[0,2]
【答案】D
【解析】由题意,不妨设 , ,
①当 时,由一元二次函数的性质可知, 在 上单调递增,
故对于 , ,这与 是函数 的最小值矛盾;
②当 时, , ,
由一元二次函数的性质可知, 在 单调递减,
故对于 , ,
当 时, 在 时取得最小值2,
从而当 时,满足 是函数 的最小值;
③当 时,由一元二次函数性质, 在 上单调递减,故对于 , ,
当 时, 在 时取得最小值 ,
若使 是函数 的最小值,只需 且 ,解得, .
综上所述,实数a的取值范围是 .
故选:D.
17.已知函数 在 上有最大值,那么实数 的取值范围为
( )
A.(0,1) B.(1,2) C. D.
【答案】D
【解析】由题意可知 在区间 上是增函数,在区间 上是减函数,
且最大值在 处取得则 ∴ .故选:D
18.定义在R上的函数 满足 ,当 时, ,
当 时, ,则 ( )
A.336 B.338 C.337 D.339
【来源】江西省宜春市奉新县第一中学2020-2021学年高一下学期第一次月考数学试
题
【答案】B
【解析】:因为当 时, ,所以 , (1) , (2) ,
又因为 ,所以函数的周期为6, (6) ,
当 时, ,所以 (3) , (4) ,
(5) ,所以 (1) (2) (3) (4) (5) (6) ,
故 (1) (2) (3)
(1) .故选:B.
19.设函数 ,则 的表达式为( )
A. B.
C. D.
【来源】安徽省六安市第一中学2021-2022学年高一上学期期中数学试题
【答案】B
【解析】令 ,则可得
所以 ,所以 故选:B
20.已知 ,若 在 上恒成立,则实数 的取值范围
是( )
A. B. C. D.
【答案】C
【解析】作出 , 在 上的图象如下图所示:
因为 在 上恒成立,所以 的图象在 的图象的上方(可
以部分点重合),
且 ,令 ,所以 ,所以 ,根据图象可知:当 经过点 时, 有最小值, ,
当 经过点 时, 有最大值, ,
综上可知 的取值范围是 ,故选:C.
二、填空题
21.已知函数 对于任意的正实数x,y满足 ,且 ,则
=______.
【来源】黑龙江省哈尔滨第九中学校2022届高三下学期第四次模拟考试文科数学试题
【答案】4
【解析】由题可知 , .
故答案为:4.
22.函数 ,则
=_______.
【来源】甘肃省兰州市教育局第四片区2021-2022学年高二下学期期中考试数学试题
【答案】 ##2011.5
【解析】∵ ,且
∴
故答案为: .
23.已知函数 .若 ,则m=______.
【来源】山东省德州市2021-2022学年高二下学期期末数学试题
【答案】3【解析】由已知 .
, ,
故答案为:3.
24.设函数 ,若 ,则实数 的值为_____.
【来源】2.4.2 函数的表示(培优讲义)-2022年初升高数学无忧衔接
【答案】
【解析】由题意知, ;
当 时,有 ,解得 (舍去);
当 时,有 ,解得 (舍去)或 .
所以实数 的值是: .
故答案为: .
25.已知函数 ,则 _____.
【来源】湖南省永州市第二中学2021-2022学年高一上学期10月月考数学试题
【答案】 #1.125
【解析】∵ , ,
因此, .故答案为: .
26.已知函数 的定义域为 ,则函数 的定义域为
_________.
【来源】辽宁省沈阳市第二中学2021-2022学年高二下学期期末数学试题
【答案】【解析】函数 的定义域为 ,即 ,所以 ,
所以 ,即 ,
所以函数的定义域为 .
故答案为: .
27.若函数 的定义域为R,则实数a的取值范围是__________.
【答案】
【解析】 的定义域是R,则 恒成立,
时, 恒成立,
时,则 ,解得 ,
综上, .
故答案为: .
28.函数 ,若 恒成立,则实数 的取值范围为
__________.
【来源】黑龙江省哈尔滨市第三中学校2021-2022学年高二下学期期末考试数学试题
【答案】
【解析】当 时, ,
当且仅当 即 时取等号,
函数 ,若 恒成立,则 ,即
,解得 ,故答案为: .
29.若方程 ,若方程 无解,则实数t的取值范围是
______.
【来源】上海市民办南模中学2022届高三下学期3月月考数学试题
【答案】
【解析】当 时, 时, ,当 时,方程
,方程 无解,
当 时, 时, ,方程 有解 ,不符合题意.
当 时, 时, , 无解,当 时,方
程 时,方程 有解, 不符合题意.
当 时, 时, , 无解,当 时,方程
时,方程 无解.
综上,方程 无解,则实数t的取值范围是 .
故答案为:
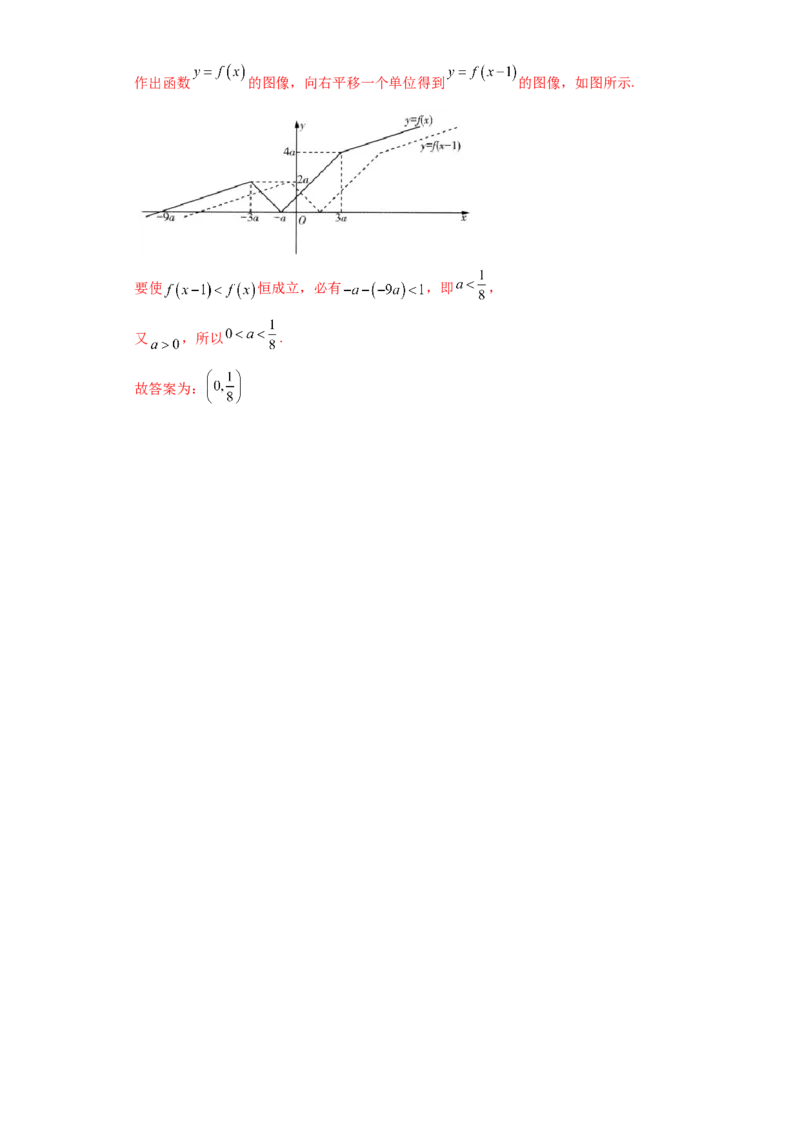
30.设 , ,若 恒成立,则实数
的取值范围是______.
【答案】
【解析】作出函数 的图像,向右平移一个单位得到 的图像,如图所示.
要使 恒成立,必有 ,即 ,
又 ,所以 .
故答案为: