文档内容
2024-2025 学年浙江省四校高一下学期 3 月联考数学试卷
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.已知复数z满足z(1+i)=i,则复数z对应的点在( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
⃗ ⃗ 1
2.已知单位向量⃗a,⃗b满足a⋅b= ,则⃗a在⃗b上的投影向量为( )
3
2 1⃗ 1⃗ 2⃗
A. ⃗b B. b C. b D. − b
3 2 3 3
3.在△ABC中,下列等式一定成立的是( )
A+B C A+B C
A. sin =−cos B. tan =−tan
2 2 2 2
C. sin(2A+2B)=−sin2C D. cos(2A+2B)=−cos2C
4.设a∈R,zi=3+ai,其中i为虚数单位.则“|z|>√10”是“a>1”的( )
A. 充分不必要条件 B. 必要不充分条件
C. 充要条件 D. 既不充分也不必要条件
5.函数f(x)=x−2+cosx,若a=f(
1
),
b=f(log
1
3)
,c=f(sin
1
),则a,b,c的大小关系为( )
2 4 2
A. a0,a≠1) a x b c
是a(即x)的函数,记为y,则y=xb,也就是我们熟悉的幂函数.事实上,由这个等式还可以得到更多的
函数模型.若令c=e,(e是自然对数的底数),将a视为自变量x(x>0,x≠1),则b为x的函数,记为
y=f (x),下列关于函数y=f (x)的叙述中正确的有( )
1
A. f (e2)=
2
1
B. ∀x∈(0,1)∪(1,+∞),ef(x)=
x
第 页,共 页
2 1C. 若 ,且 , 均不等于 , ,则
m>n>0 m n 1 |f (m)|=|f (n)| m2+4n2≥4
D. 若对任意 ,不等式 恒成立,则实数 的值为
x∈(0,1)∪(1,+∞) (mx2+x+2m−1)f (x)>0 m 0
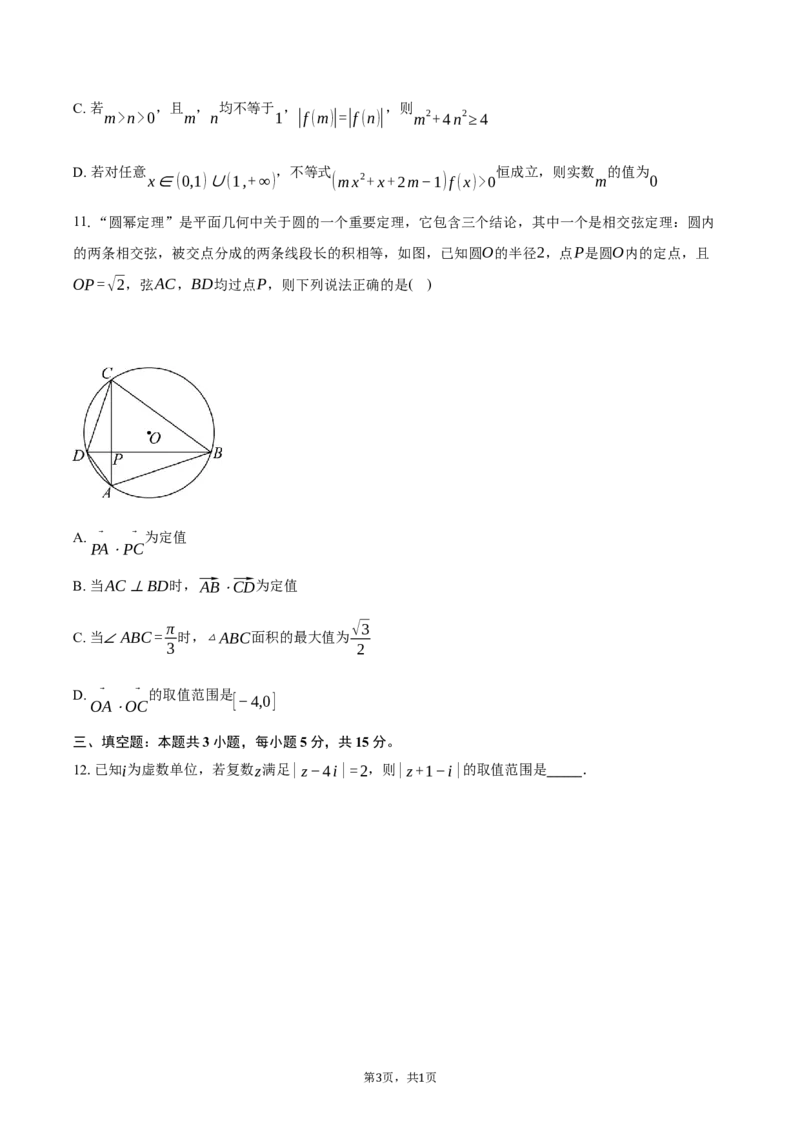
11.“圆幂定理”是平面几何中关于圆的一个重要定理,它包含三个结论,其中一个是相交弦定理:圆内
的两条相交弦,被交点分成的两条线段长的积相等,如图,已知圆O的半径2,点P是圆O内的定点,且
OP=√2,弦AC,BD均过点P,则下列说法正确的是( )
A. ⃗ ⃗ 为定值
PA⋅PC
B. 当AC⊥BD时,⃗AB⋅⃗CD为定值
π √3
C. 当∠ABC= 时,△ABC面积的最大值为
3 2
D. ⃗ ⃗ 的取值范围是
[−4,0]
OA⋅OC
三、填空题:本题共3小题,每小题5分,共15分。
12.已知i为虚数单位,若复数z满足|z−4i|=2,则|z+1−i|的取值范围是 .
第 页,共 页
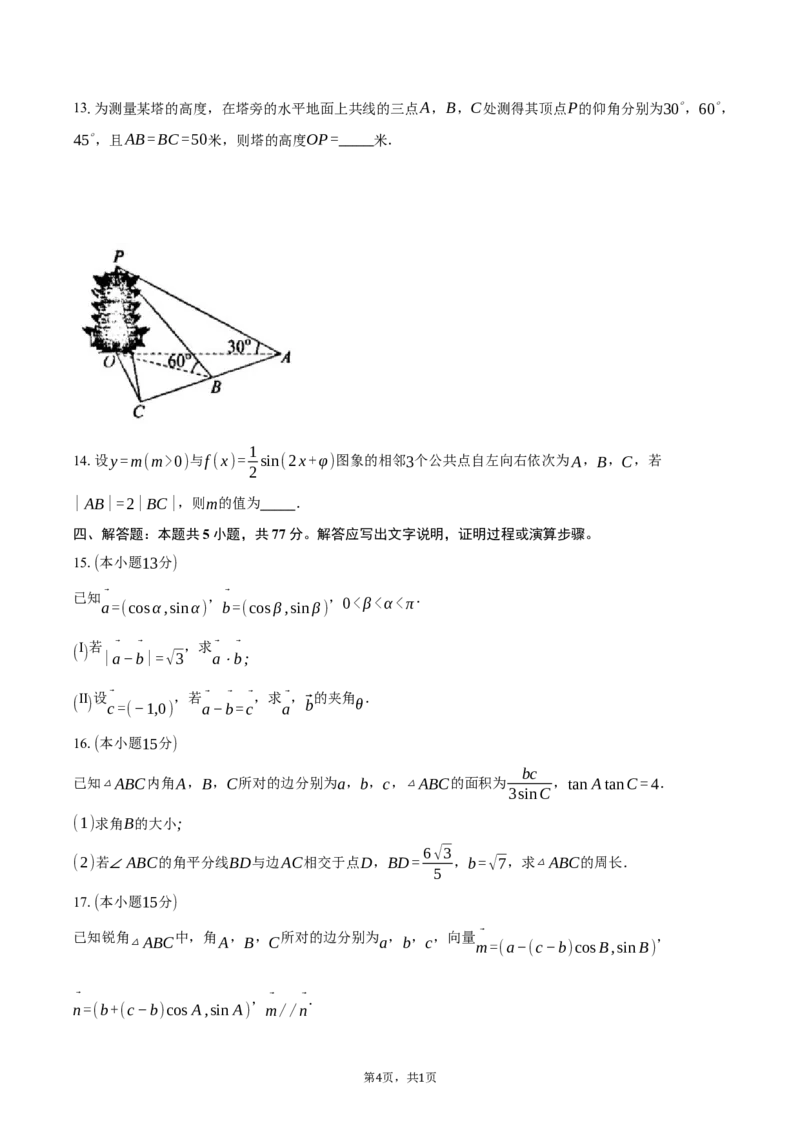
3 113.为测量某塔的高度,在塔旁的水平地面上共线的三点A,B,C处测得其顶点P的仰角分别为30∘,60∘,
45∘,且AB=BC=50米,则塔的高度OP= 米.
1
14.设y=m(m>0)与f(x)= sin(2x+φ)图象的相邻3个公共点自左向右依次为A,B,C,若
2
|AB|=2|BC|,则m的值为 .
四、解答题:本题共5小题,共77分。解答应写出文字说明,证明过程或演算步骤。
15.(本小题13分)
已知⃗
a=(cosα,sinα)
,⃗
b=(cosβ,sinβ)
, 0<β<α<π .
Ⅰ 若 ⃗ ⃗ ,求⃗ ⃗
( ) |a−b|=√3 a⋅b;
( Ⅱ ) 设⃗ c=(−1,0) ,若⃗ a− ⃗ b= ⃗ c ,求⃗ a , ⃗b 的夹角 θ .
16.(本小题15分)
bc
已知△ABC内角A,B,C所对的边分别为a,b,c,△ABC的面积为 ,tan AtanC=4.
3sinC
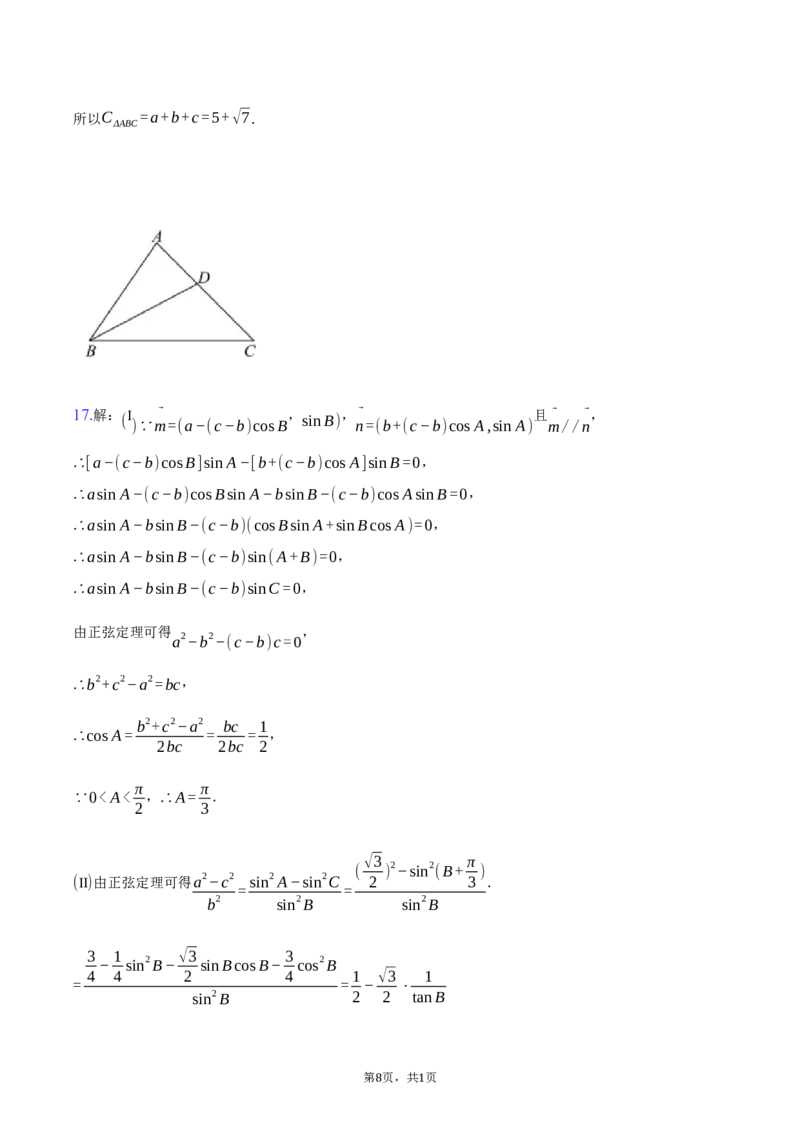
(1)求角B的大小;
6√3
(2)若∠ABC的角平分线BD与边AC相交于点D,BD= ,b=√7,求△ABC的周长.
5
17.(本小题15分)
已知锐角 中,角 , , 所对的边分别为 , , ,向量⃗ ,
△ABC A B C a b c m=(a−(c−b)cosB,sinB)
⃗ ,⃗ ⃗.
n=(b+(c−b)cosA,sin A) m//n
第 页,共 页
4 1(Ⅰ)求A;
Ⅱ
求a2−c2的取值范围.
( )
b2
18.(本小题17分)
ωx 2π
已知函数f(x)=sinωx+2√3cos2 −√3,(ω>0)满足f(x− )+f(−x)=0,且f(x)在区间
2 3
π π
(− , )上单调递增.
3 6
(Ⅰ)求ω的值;
(Ⅱ)设a∈[0,2π].若函数y=f(x)和y=f(x+a)在[0,π]上有相同的最大值,求a的取值范围.
19.(本小题17分)
定义在 上的函数 ,如果对任意的 ,都有 成立,
(0,+∞) f(x) x∈(0,+∞) f(kx)=kf(x)(k≥2,k∈N∗)
则称f(x)为k阶伸缩函数.
( Ⅰ ) 若函数f(x) 为二阶伸缩函数,且当x∈(1,2] 时,f(x)=1+log 1 x,求 f(2√3) 的值.
3
Ⅱ 若 为三阶伸缩函数,且当 时, ,求证:函数 在
( ) f(x) x∈(1,3] f(x)=√3x−x2 y=f(x)−√2x (1,+∞)
上无零点.
(Ⅲ)若函数f(x)为k阶伸缩函数,且当x∈(1,k]时,f(x)的取值范围是[0,1),求f(x)在
上的取值范围.
(0,kn+1 ](n∈N∗)
第 页,共 页
5 1参考答案
1.A
2.C
3.C
4.B
5.B
6.A
7.D
8.C
9.AC
10.ACD
11.ABD
12.[√10−2,√10+2]
13.10√15
1
14.
4
15.解: Ⅰ 由题意得 ⃗ ⃗ ,即 ⃗ ⃗ ⃗ ⃗ ⃗ ⃗ ,
( ) |a−b|2=3 (a−b) 2=a2−2a⋅b+b2=3
1
又因为 ⃗ a2= ⃗ b2=| ⃗ a|2=| ⃗ b|2=1 ,所以 2−2 ⃗ a⋅ ⃗ b=3 ,即⃗a⋅⃗b=−
2
;
Ⅱ 由题意得 ⃗ ⃗ ⃗ ,即⃗ ⃗ ⃗ ⃗ ⃗ ;
( ) (a−b) 2=c2 a2−2a⋅b+b2=c2
又⃗ ,⃗ ⃗
c=(−1,0) a=(cosα,sinα),b=(cosβ,sinβ),0<β<α<π
所以⃗ ⃗ ⃗ ⃗ ⃗ ⃗ ,
a2=b2=c2=|a|2=|b|2=|c|2=1
1
所以
1−2
⃗
a⋅
⃗
b+1=1
,即⃗a⋅⃗b=
2
,
1
⃗ ⃗
所以
cosθ=
a⋅b
=
2
=
1,又
θ∈[0,π]
,
⃗ ⃗ 1×1 2
|a||b|
π
所以θ= .
3
第 页,共 页
6 11 bc 2
16.解:(1)由题意知:S = bcsin A= ,所以sin AsinC= ,
△ABC 2 3sinC 3
sin AsinC 1
因为tan AtanC= =4,所以cosAcosC= ,
cosAcosC 6
1 2 1
所以cos(A+C)=cosAcosC−sin AsinC= − =− ,
6 3 2
1
因为A+B+C=π,所以cosB=cos[π−(A+C)]=−cos(A+C)= ,
2
π
因为0 0< <√3 ∴−1< − ⋅ < ∴ (−1, ).
3 tanB 2 2 tanB 2 b2 2
ωx
18.解:(Ⅰ)f(x)=sinωx+2√3cos2 −√3
2
1+cosωx
=sinωx+2√3⋅ −√3
2
=sinωx+√3cosωx
π
=2sin(ωx+ ),
3
2π π
由条件f(x− )+f(−x)=0知(− ,0)为函数f(x)的对称中心,
3 3
π π
故− ω+ =kπ(k∈Z),解得ω=−3π+1(k∈Z),
3 3
π π π π π π π π π
当x∈(− , )时,ωx+ ∈(− ω+ , ω+ )⊆(− , ),
3 6 3 3 3 6 3 2 2
π π π
{− ω+ ⩾−
从而 3 3 2,解得 ,
ω⩽1
π π π
ω+ ⩽
6 3 2
又ω>0且ω=−3π+1(k∈Z),
所以ω=1;
第 页,共 页
9 1π
(Ⅱ)由(Ⅰ)知f(x)=2sin(x+ ),
3
π π 4π
若x∈[0,π]时, ≤x+ ≤ ,
3 3 3
π π
当x+ = 时,函数y=f(x)取得最大值,即f(x) =2,
3 2 max
而函数y=f(x+a)与y=f(x)存在相同的最大值,
π π
故当x+a+ = +2kπ(k∈Z)时,函数y=f(x+a)在[0,π]内取得最大值,
3 2
π
因此可得x= +2kπ−a∈[0,π],
6
π
{ −a⩾0
6
当 时,可得π ,则有 ,解得 π
① k=0 −a∈[0,π] π a∈[0, ];
6 −a⩽π 6
6
0⩽a⩽2π
13π
{ −a⩾0
6
当 时,可得13π ,则有 ,解得 7π ,
② k=1 −a∈[0,π] 13π a∈[ ,2π]
6 −a⩽π 6
6
0⩽a⩽2π
π π 13π π
当k≥2时,x= +2kπ−a≥ +4π−2π≥ ,此时,x= +2kπ−a∉[0,π],
6 6 6 6
π π 11π π
当k≤−1时,x= +2kπ−a≤ −2π=− ,此时,x= +2kπ−a∉[0,π],
6 6 6 6
π 7π
综上所述,a的取值范围为[0, ]∪[ ,2π].
6 6
第 页,共 页
10 119.解: (1) 由题设,当x∈(1,2] 时,f(x)=1+log 1 x,
3
1 1
∴f(√3)=1+log √3=1− = .
1 2 2
3
∵函数f(x)为二阶伸缩函数,
∴对任意x∈(0,+∞),都有f(2x)=2f(x).
∴f(2√3)=2f(√3)=1.
x
(2)当x∈(3m,3m+1 ](m∈N∗)时, ∈(1,3].
3m
由f(x)为三阶伸缩函数,有f(3x)=3f(x).
时, .
∵x∈(1,3] f(x)=√3x−x2
∴f(x)=3f( x )=32f( x )=…=3mf( x )=3m √ 3⋅( x )−( x ) 2=√3m+1 ⋅x−x2 .
3 32 3m 3m 3m
令 ,解得 或 ,它们均不在 内.
f(x)−√2x=0 x=0 x=3m (3m,3m+1 ]
∴函数y=f(x)−√2x在(1,+∞)上无零点.
(3) 由题设,若函数f(x)为k阶伸缩函数,有f(kx)=kf(x),
且当x∈(1,k]时,f(x)的取值范围是[0,1).
x
∴当x∈(kn,kn+1 ]时,f(x)=knf( ).
kn
x x
∵ ∈(1,k],所以f( )∈[0,1).
kn kn
当 时,
∴ x∈(kn,kn+1 ] f(x)∈[0,kn ).
当x∈(0,1]时,即0