文档内容
2024-2025 学年浙江省卓越联盟高一下学期 5 月阶段性联考
数学试卷
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.已知集合A={x|10
√3 √3 √3 √3
A. B. 1- C. - D. 1+
2 2 2 2
5.轴截面为正方形的圆柱,侧面积为 ,体积为 ,若 ,则底面半径是( )
S(m2 ) V(m3 ) S=V
A. 1(m) B. π(m) C. 2π(m) D. 2(m)
1 1
6.已知a=log ( ),b=40.3,c=log ( ),则a,b,c的大小关系是( )
3 5 1 2
3
A. b>c>a B. b>a>c C. c>b>a D. c>a>b
7.已知二次函数 ,若不等式 的解集为 ,则函数 图像为
f(x)=ax2+bx+c f(x)≥0 [-1,2] g(x)=f(1-x)
( )
1 3
A. 开口向上,对称轴为x= 的抛物线 B. 开口向上,对称轴为x= 的抛物线
2 2
1 3
C. 开口向下,对称轴为x= 的抛物线 D. 开口向下,对称轴为x= 的抛物线
2 2
第 页,共 页
1 38.在△ABC中,点D是BC的中点,点E在线段AC上,且AE:EC=2:1,AD和BE相交于点F,则
AF:FD的值为( )
A. 1:1 B. 2:1 C. 3:1 D. 4:1
二、多选题:本题共3小题,共18分。在每小题给出的选项中,有多项符合题目要求。
9.已知ABCD-A B C D 为正方体,F-A B C D ,E-ABCD均为正四棱锥,所有棱长均为1,则
1 1 1 1 1 1 1 1
下列说法正确的是( )
A. AE//FC
1
B. 在棱所在的直线中,与直线AB异面的共有10条
1+√2
C. 以E为顶点,正方形ABCD外接圆为底面的圆锥的表面积是 π
2
√2
D. 以E为顶点,正方形ABCD外接圆为底面的圆锥的体积是 π
4
10.设复数z ,z (z ≠0),z为z的共轭复数,下列说法正确的有( )
1 2 1
A. 若 ,则 B. 若 ,则 z 1
|z |=1 |z z |=|z | |z |=1 | 2|=
2 1 2 1 2 z |z |
1 1
C. 若 ,则 D. 若 ,则
|z +z |=|z -z | z z =0 z2+z2=0 z =z =0
1 2 1 2 1 2 1 2 1 2
2
11.已知⃗a=(1,0),⃗b=(-1,1),函数f(x)=kx+ ,此函数图象上任意一点P(x,y),均满足
x
⃗ ⃗ ⃗ ⃗
(OP⋅a)⋅(OP⋅b)
为定值。过点P做y轴的平行线,交y=x于点B,过点P做y=x的平行线,交y轴于点
第 页,共 页
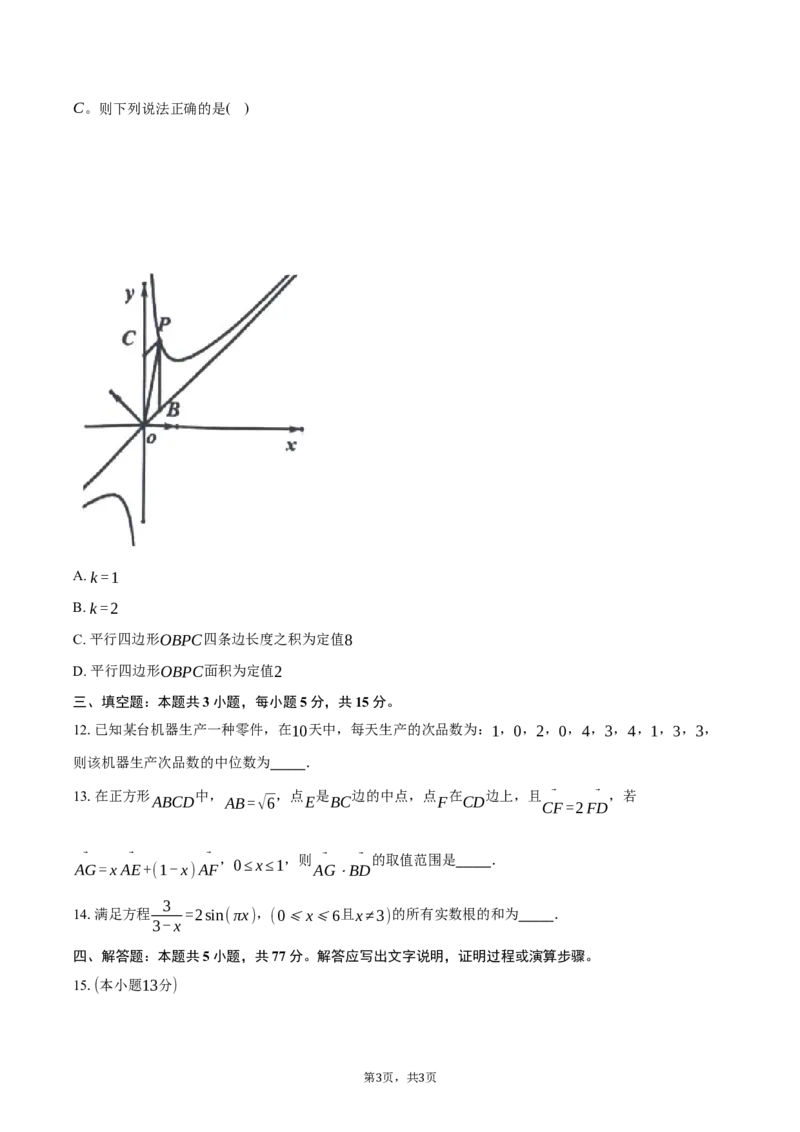
2 3C。则下列说法正确的是( )
A. k=1
B. k=2
C. 平行四边形OBPC四条边长度之积为定值8
D. 平行四边形OBPC面积为定值2
三、填空题:本题共3小题,每小题5分,共15分。
12.已知某台机器生产一种零件,在10天中,每天生产的次品数为:1,0,2,0,4,3,4,1,3,3,
则该机器生产次品数的中位数为 .
13.在正方形 中, ,点 是 边的中点,点 在 边上,且 ⃗ ⃗ ,若
ABCD AB=√6 E BC F CD
CF=2FD
A
⃗
G=x A
⃗
E+(1-x)A
⃗
F
,
0≤x≤1
,则
A
⃗
G⋅B
⃗
D
的取值范围是 .
3
14.满足方程 =2sin(πx),(0⩽x⩽6且x≠3)的所有实数根的和为 .
3-x
四、解答题:本题共5小题,共77分。解答应写出文字说明,证明过程或演算步骤。
15.(本小题13分)
第 页,共 页
3 3记△ABC的内角A,B,C的对边分别为a,b,c(a,b,c互不相等),已知acosC=(2a-c)cosA,点A
与点D分别在直线BC的异侧,且BD=CD=3。
(1)求证:B=2A;
π
(2)若AC=√3BC,∠BCD= ,求线段AD的长。
3
16.(本小题15分)
甲乙两个同学想对本市20岁以上的人群做一个网络消费水平的研究,已知本市20岁以上的人群男女性别比
例为21:20。两人决定用分层抽样的方法,随机选一部分人了解月平均网购水平。甲负责男性,乙负责女
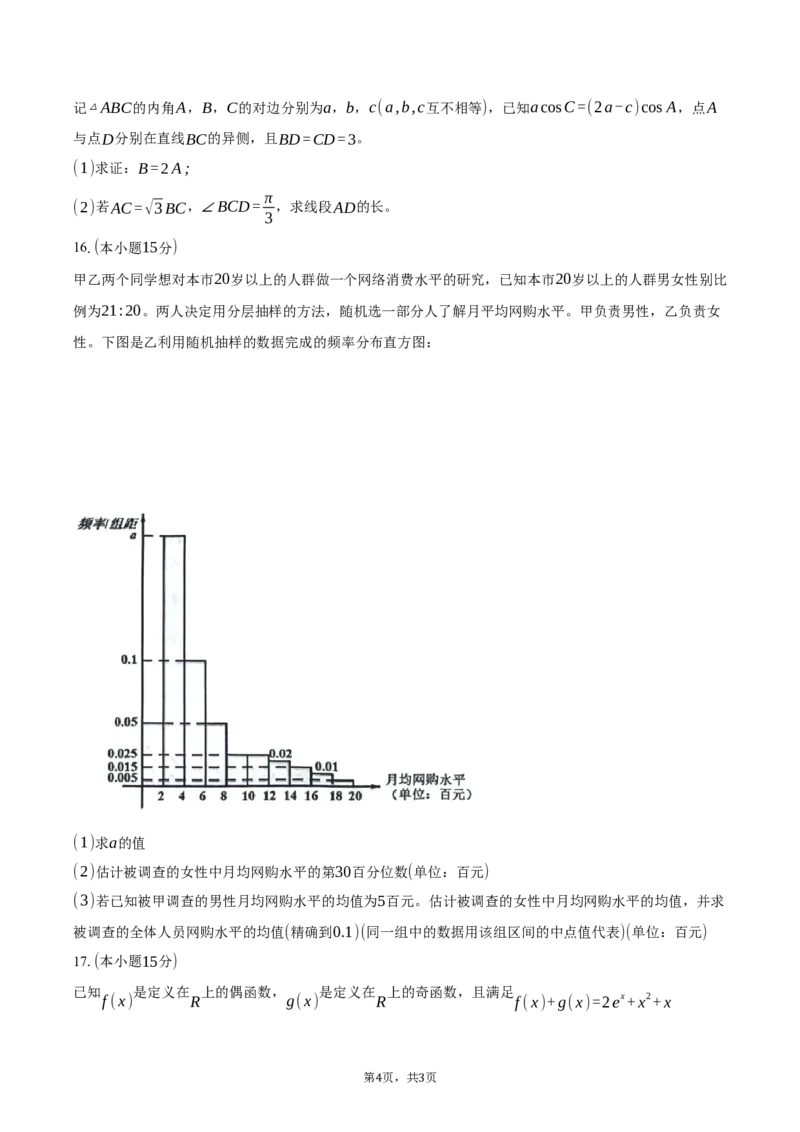
性。下图是乙利用随机抽样的数据完成的频率分布直方图:
(1)求a的值
(2)估计被调查的女性中月均网购水平的第30百分位数(单位:百元)
(3)若已知被甲调查的男性月均网购水平的均值为5百元。估计被调查的女性中月均网购水平的均值,并求
被调查的全体人员网购水平的均值(精确到0.1)(同一组中的数据用该组区间的中点值代表)(单位:百元)
17.(本小题15分)
已知 是定义在 上的偶函数, 是定义在 上的奇函数,且满足
f(x) R g(x) R f(x)+g(x)=2ex+x2+x
第 页,共 页
4 3(1)求f(x)与g(x)的解析式;
1 1
(2)设函数h(x)=f(x)+g(x),且h(x2-2x+ )≥h(2x2- )恒成立,求实数x的取值范围。
2 2
18.(本小题17分)
π
已知函数f(x)=√3sin(ωx+φ)+1,(ω>0,0<φ<π),满足相邻两条对称轴之间的距离为 ,
2
π
f(x)≤f( )对任意实数x恒成立。
6
(1)求函数f(x)的解析式;
π 1
(2)将函数f(x)的图象向右平移 ,再把各点横坐标缩小为原来的 (纵坐标不变),得到函数g(x)的图象,
6 2
π π
当x∈[- , ]时,求g(x)的值域;
8 8
π
(3)当x∈[0, ]时,解不等式f(x)≥sinx+1
2
19.(本小题17分)
如图,已知EA,CD垂直于Rt△ABC所在平面,且位于平面ABC同侧,∠ACB=90∘,CD=1,
AE=AC=BC=2。
(1)判断并证明以点D为球心,√3为半径的球与平面ABE的位置关系(当球心到平面α的距离等于半径时,
球与平面α相切,当球心到平面α的距离小于半径时,球与平面α相交,当球心到平面α的距离大于半径时,
球与平面α相离);
(2)以点D为球心√3为半径的球与线段BD交于点G,与线段DE交于点F,求直线GF与平面BCD所成角
的正弦值;
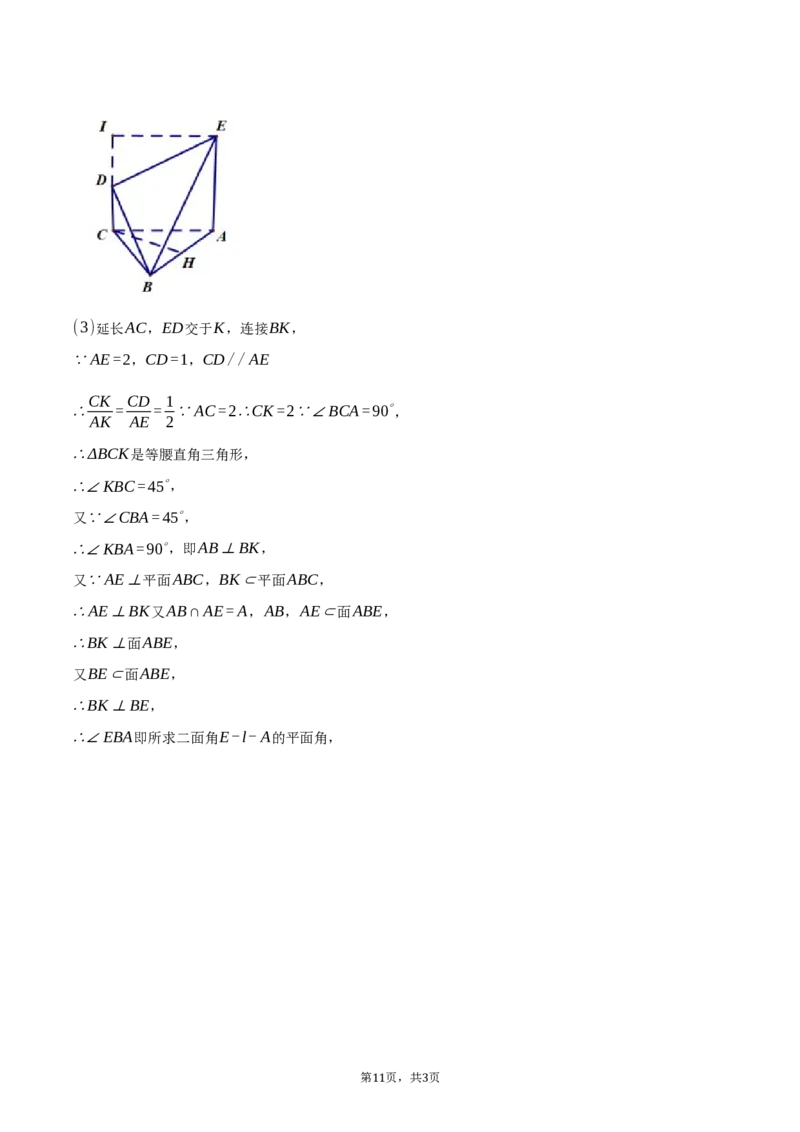
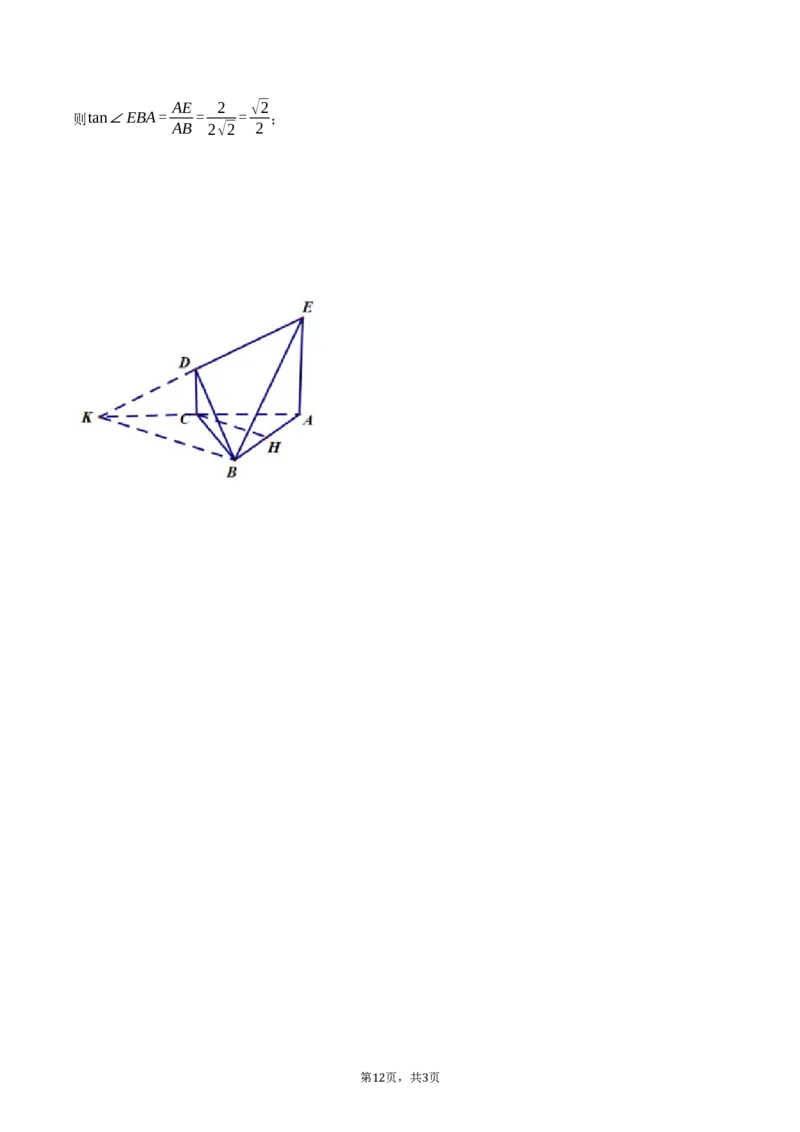
(3)若平面BDE与平面ABC交于l,求二面角E-l-A的正切值。
第 页,共 页
5 3参考答案
1.A
2.B
3.C
4.B
5.D
6.A
7.C
8.D
9.ABC
10.AB
11.ACD
12.2.5
13.[-3,4]
14.12
15.解:(1) ∵acosC=(2a-c)cosA,
∴sin AcosC=2sin AcosA-sinCcosA,
∴sin AcosC+sinCcosA=2sin AcosA,
∴sin(A+C)=sin2A,
∴sinB=sin2A,
∴B=2A或B+2A=π,此时A=C(舍),
∴B=2A;
π
(2)∵BD=CD=3,∠BCD= ,
3
π
∴∠DBC=∠DCB= ,
3
∴△BCD为正三角形,
∴BC=3,
∴AC=√3BC=3√3,
第 页,共 页
6 3b a
由(1)知 = ,
sin2A sin A
3√3 3
∴ = ,
2sin AcosA sin A
√3
∴cosA= ,
2
π π π
∴A= ,B= ,∴∠BCA= ,
6 3 2
∴AB=2BC=2×3=6,
2π
∴∠ABD= ,
3
2π 1
∴ AD2=AB2+BD2-2⋅AB⋅BD⋅cos =36+9-2×3×6×(- )=63,
3 2
∴AD=3√7.
16.(1)∵组距为2,∴0.05+a+0.1+0.05+0.025+0.025+0.02+0.015+0.01+0.005=0.5∴a=0.2
0.2
(2)∵0.05×2=0.1∵ =1∴第30百分位数是2+1=3(百元)
0.2
(3)设女性月均网购水平的均值为x,
男性月均网购水平的均值为y,
n m 20 21
x=1×0.1+3×0.4+5×0.2+7×0.1+9×0.05+11×0.05+13×0.04+15×0.03+17×0.02+19×0.01=5.5ω= x+ y= ×5.5+ ×5=5.2
n+m n+m 41 41
17.解:
(1)∵f(-x)+g(-x)=2e-x+x2-x
∵f(x)是偶函数,g(x)是奇函数
∴f(x)-g(x)=2e-x+x2-x∵f(x)+g(x)=2ex+x2+x
1 1 1
∴f(x)=ex+e-x+x2g(x)=ex-e-x+x(2)∵x2-2x+ =(x-1) 2- ∈[- ,+∞),
2 2 2
第 页,共 页
7 31 1
2x2- ∈[- ,+∞)
2 2
1
设- 0∴(x -x )(x +x +1)<0,2(ex 1-ex 2)<0∴h(x )-h(x )<0∴h(x)在
2 1 2 1 2 1 2 1 2 1 2
1
(- ,+∞)上单调递增
2
1 1
∴x2-2x+ ≥2x2- ∴x2+2x-1≤0∴x∈[-1-√2,-1+√2].
2 2
π
18.解:(1)∵两条相邻对称轴之间的距离为 ,
2
∴T=π∴ω=2,
π
又∵f(x)≤f( )
6
π π π
∴x= 时f(x)取最大值,即2× +φ= +2kπ,k∈Z,
6 6 2
π
∴φ= +2kπ,k∈Z,
6
π
又∵0<φ<π∴φ= ,
6
π π
∴f(x)=√3sin(2x+ )+1(2)由(1)得f(x)=√3sin(2x+ )+1,
6 6
π
将函数f(x)的图象向右平移 ,得
6
π π π π π
y=√3sin[2(x- )+ ]+1=√3sin(2x- + )+1=√3sin(2x- )+1,
6 6 3 6 6
第 页,共 页
8 31 π
再把所得函数图像各点横坐标缩小为原来的 (纵坐标不变),得到g(x)=√3sin(4x- )+1,
2 6
π π π 2π π π √3
∵x∈[- , ],∴4x- ∈[- , ],∴sin(4x- )∈[-1, ],
8 8 6 3 3 6 2
5 5
∴g(x)∈[1-√3, ],即g(x)的值域为[1-√3, ].
2 2
π
(3)f(x)≥sinx+1⇔√3sin(2x+ )≥sinx,
6
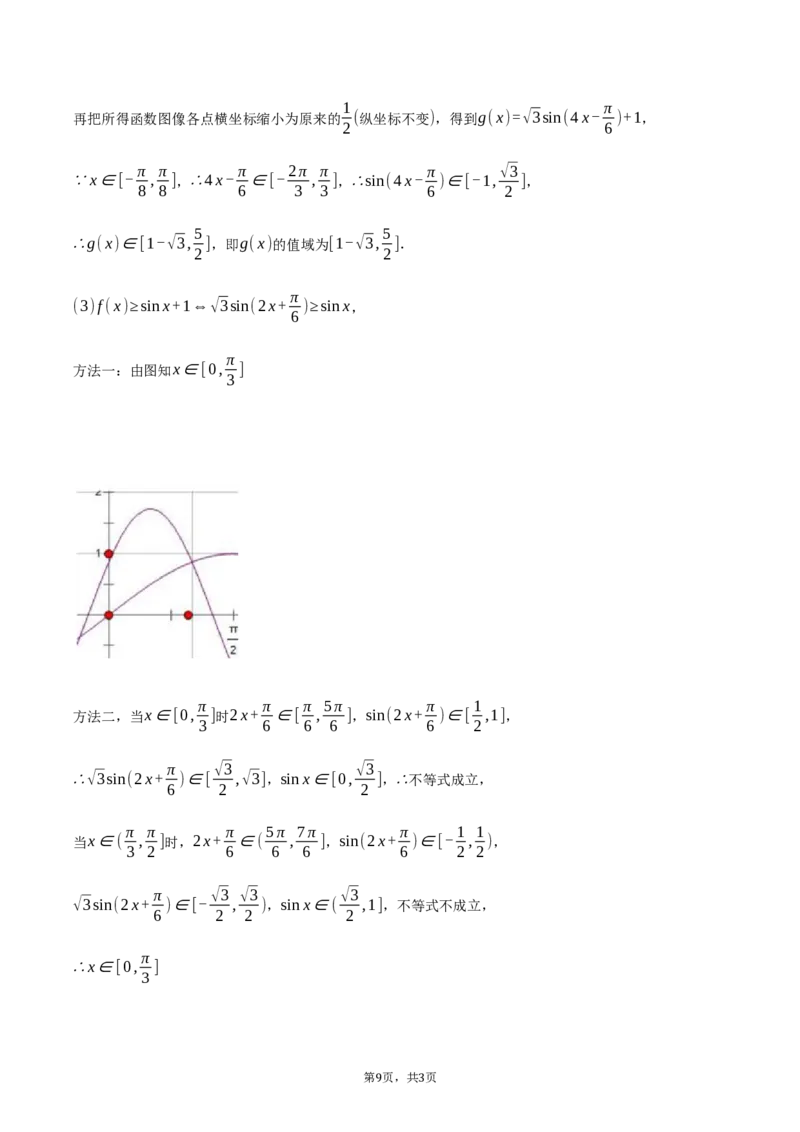
π
方法一:由图知x∈[0, ]
3
π π π 5π π 1
方法二,当x∈[0, ]时2x+ ∈[ , ],sin(2x+ )∈[ ,1],
3 6 6 6 6 2
π √3 √3
∴√3sin(2x+ )∈[ ,√3],sinx∈[0, ],∴不等式成立,
6 2 2
π π π 5π 7π π 1 1
当x∈( , ]时,2x+ ∈( , ],sin(2x+ )∈[- , ),
3 2 6 6 6 6 2 2
π √3 √3 √3
√3sin(2x+ )∈[- , ),sinx∈( ,1],不等式不成立,
6 2 2 2
π
∴x∈[0, ]
3
第 页,共 页
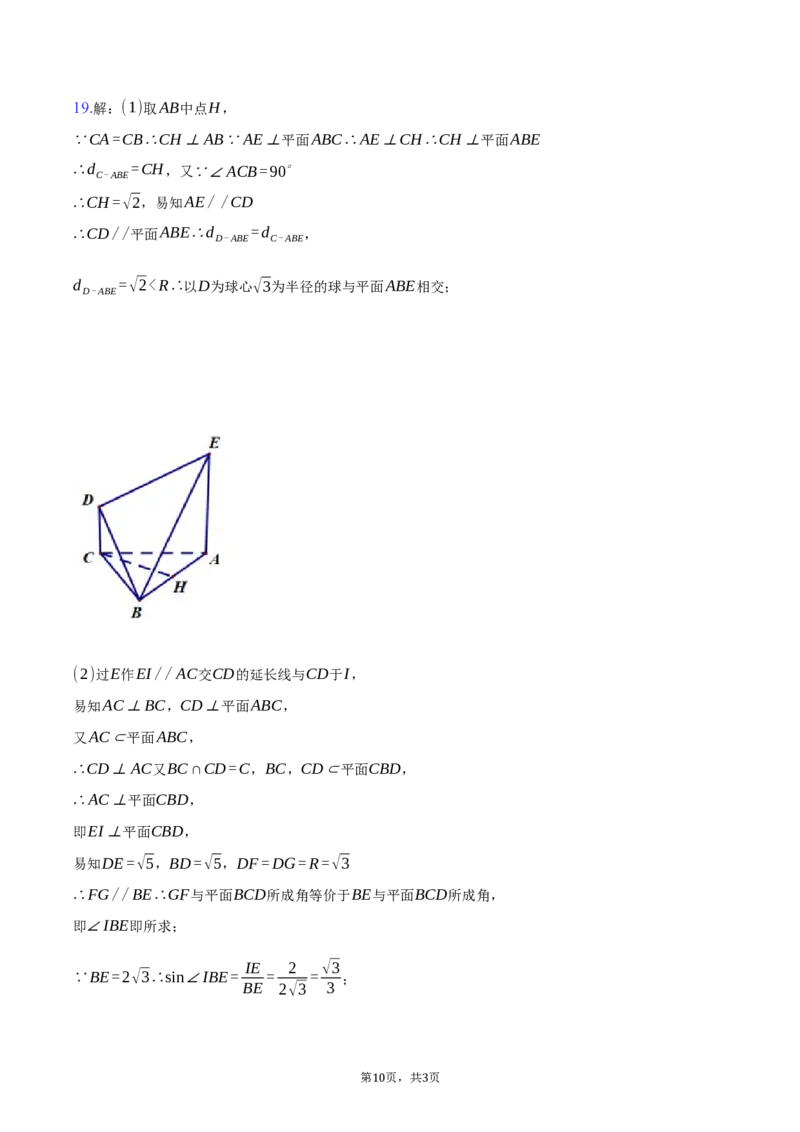
9 319.解:(1)取AB中点H,
∵CA=CB∴CH⊥AB∵AE⊥平面ABC∴AE⊥CH∴CH⊥平面ABE
∴d =CH,又∵∠ACB=90∘
C-ABE
∴CH=√2,易知AE//CD
∴CD//平面ABE∴d =d ,
D-ABE C-ABE
d =√2