专题32离散型随机变量的数字特征（解析版）_E015高中全科试卷_数学试题_选修3_05.专项训练_专题32离散型随机变量的数字特征-高中数学新教材人教A版选择性必修配套提升训练

专题32 离散型随机变量的数字特征 一、单选题 x x x x 1．（2020·尤溪县第五中学高一期末）若一组数据 1， 2， 3，…， n的平均数为2，方差为3，则 2x 5 2x 5 2x 5 2x 5 1 ， 2 ， 3 ，…， n 的平均数和方差分别是（ ） A．9，11 B．4，11 C．9，12 D．4，17 【答案】C 【解析】 E(x)  2,D(x) 3 E(2x5)2E(x)59 D(2x522D(x)12 由题 ，则 ， . 故选：C X E(X) 2．（2020·海林市朝鲜族中学高二期末（理））若随机变量 的分布列如下表，则 （ ） X 0 1 2 3 4 5 P 2x 3x 7x 2x 3x x 1 1 9 20 A．18 B．9 C．20 D． 9 【答案】D 【解析】 1 20 2x3x7x2x3xx1x ,E(X)3x14x6x12x5x40x  18 9 1 3．（2020·浙江宁波高二期末）已知随机变量的取值为 ii 0,1,2 .若 P0 5， E1 ，则 D23 （ ） 2 4 8 16 A．5 B．5 C．5 D． 5【答案】C 【解析】 1 4 P21  p  p 由题意，设P1 p，则 5 5 ， 1 4  3 E  p2   p  1 p 又 5 5  ，解得 5， 3 1 P1 P2 所以 5， 5 ， 1 3 1 2 D 102  112  122  则 5 5 5 5， 8 D234D 所以 5. 故选：C. E2X 1 4．（2020·广东东莞高二期末）随机变量X 的分布列如下表所示，则 （ ） X 2 1 1 1 1 a P 6 3 1  A．0 B． 2 C．1 D．2 【答案】D 【解析】 1 1 1 a 1 a  由随机变量的分布列的性质，可得6 3 ，解得 2， 1 1 1 1 EX2 (1) 1  则 6 2 3 2 ，1 E2X 12EX12( )12 所以 2 . 故选：D. 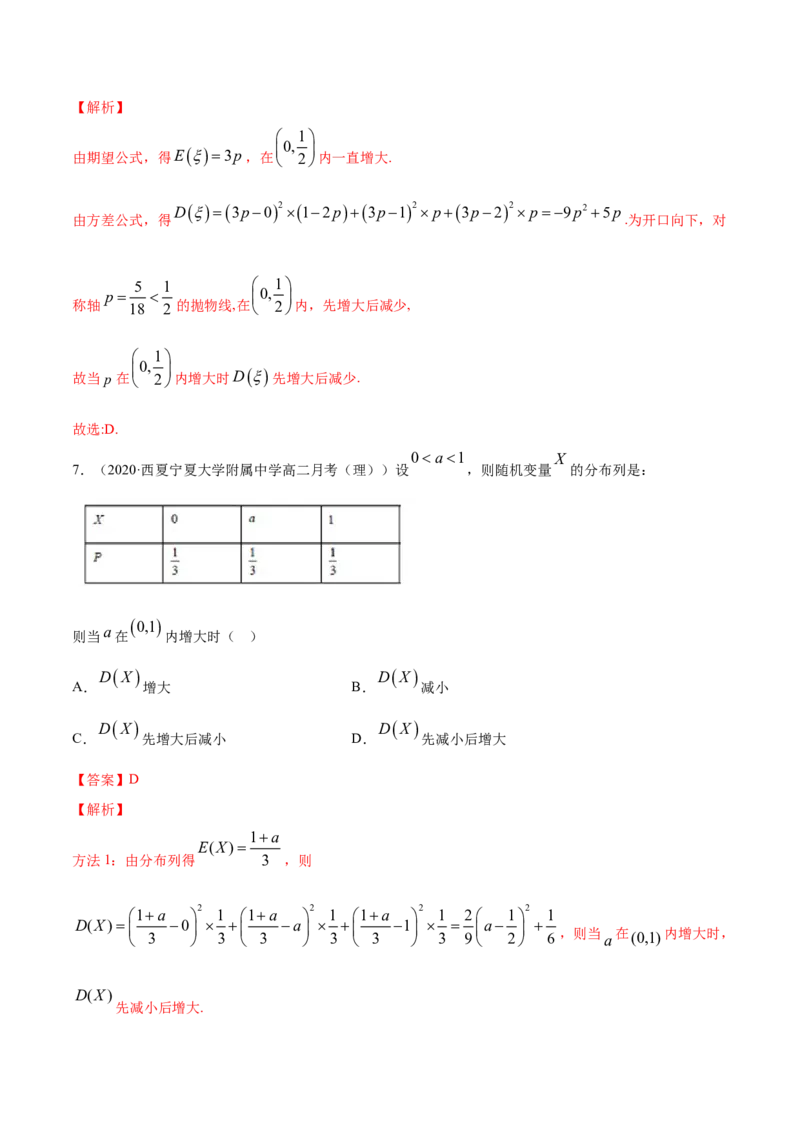5．（2020·渝中重庆巴蜀中学高二期末）随机变量X的取值范围为0，1，2，若 1 P(X 0) , E(X)1 4 ，则D（X）＝（ ） 1 2 1 3 A．4 B． 2 C．2 D．4 【答案】C 【解析】 P(X 1) p P(X 2)q 设 ， ， 1 1 由题意，E(X)0  p2q1，且  pq1， 4 4 1 1 p q 解得 2， 4， 1 1 1 1 D(X) (01)2  (11)2  (21)2  ， 4 2 4 2 故选：C． 1  1 0 p  0,  6．（2020·浙江西湖学军中学高三其他）设 2 ，随机变量的分布如下表所示，则当 p在 2 内增大时，（ ）  0 1 2 p 12p p p E E A． 先减少后增大 B． 先增大后减少 D D C． 先减小后增大 D． 先增大后减小 【答案】D【解析】  1 0, 由期望公式，得E3p，在   2  内一直增大. D3p02 12p3p12  p3p22  p9p25p 由方差公式，得 .为开口向下，对 5 1  1 p   0,  称轴 18 2 的抛物线,在 2内，先增大后减少,  1 0, 故当 p在   2  内增大时D 先增大后减少. 故选:D. 0a1 X 7．（2020·西夏宁夏大学附属中学高二月考（理））设 ，则随机变量 的分布列是： 0,1 a 则当 在 内增大时（ ） DX DX A． 增大 B． 减小 DX DX C． 先增大后减小 D． 先减小后增大 【答案】D 【解析】 1a E(X) 方法1：由分布列得 3 ，则 2 2 2 2 1a  1 1a  1 1a  1 2 1 1 D(X) 0   a   1   a          ，则当 在 内增大时，  3  3  3  3  3  3 9 2 6 a (0,1) D(X) 先减小后增大.方法2：则 D(X) E  X2 E(X)0 a2  1  (a1)2  2a2 2a2  2    a 1  2  3  3 3 9 9 9  2 4 故选D. i 1,2 8．（2020·浙江海曙效实中学高三其他）盒中有5个小球，其中3个白球，2个黑球，从中任取i X i 1,2 个球，在取出的球中，黑球放回，白球涂黑后放回，此时盒中黑球的个数记为 i ，则（ ） PX 2 PX 2 EX  EX  A． 1 2 ， 1 2 PX 2 PX 2 EX  EX  B． 1 2 ， 1 2 PX 2 PX 2 EX  EX  C． 1 2 ， 1 2 PX 2 PX 2 EX  EX  D． 1 2 ， 1 2 【答案】C 【解析】 C1 2 C2 1 PX 2 2  PX 2 2   PX 2 1 C1 5 ， 2 C2 10 1 ， 5 5 PX 3 C 3 1  3 EX  13 ∵ 1 C1 5，∴ 1 5 . 5 PX 2 1 PX 3 C 3 1C 2 1  6 PX 4 C 3 2  3 ∵ 2 10 ， 2 C2 10 ， 2 C2 10 ， 5 5 16 EX   EX  ∴ 2 5 1 ， 故选：C. 二、多选题 1 PX 0 9．（2020·江苏海陵泰州中学高二月考）若随机变量X服从两点分布，其中 3，E（X）、D（X）分别为随机变量X均值与方差，则下列结论正确的是（ ） A．P（X＝1）＝E（X） B．E（3X+2）＝4 4 DX C．D（3X+2）＝4 D． 9 【答案】AB 【解析】 1 PX 0 随机变量X服从两点分布，其中 3， 2  ∴P（X＝1） 3， 1 2 2 0 1  E（X） 3 3 3， 2 1 2 2 2       D（X）＝（0 3 ）2 3 （1 3 ）2 3 9 ， 在A中，P（X＝1）＝E（X），故A正确； 2  2 在B中，E（3X+2）＝3E（X）+2＝3 3 4，故B正确； 2   在C中，D（3X+2）＝9D（X）＝9 9 2，故C错误； 2  在D中，D（X） 9 ，故D错误. 故选：AB. 10．（2020·海南海口高三其他）小张上班从家到公司开车有两条线路，所需时间（分钟）随交通堵塞状况 有所变化，其概率分布如下表所示： 所需时间（分钟） 30 40 50 60 线路一 0.5 0.2 0.2 0.1 线路二 0.3 0.5 0.1 0.1则下列说法正确的是（ ） A．任选一条线路，“所需时间小于50分钟”与“所需时间为60分钟”是对立事件 B．从所需的平均时间看，线路一比线路二更节省时间 C．如果要求在45分钟以内从家赶到公司，小张应该走线路一 D．若小张上、下班走不同线路，则所需时间之和大于100分钟的概率为0.04 【答案】BD 【解析】 对于选项A，“所需时间小于50分钟”与“所需时间为60分钟”是互斥而不对立事件，所以选项A错误； 对于选项B，线路一所需的平均时间为300.5400.2500.2690.139分钟， 线路二所需的平均时间为300.3400.5500.1600.140分钟， 所以线路一比线路二更节省时间，所以选项B正确； C 对于选项 ，线路一所需时间小于45分钟的概率为0.7，线路二所需时间小于45分钟的概率为0.8，小张 应该选线路二，所以选项C错误； 50,60 60,50 对于选项D，所需时间之和大于100分钟，则线路一、线路二的时间可以为 ， 和 60,60 0.20.10.10.10.10.10.04 三种情况，概率为 ，所以选项D正确． 故选：BD. 11．（2020·山东潍坊高二期中）设离散型随机变量X 的分布列为 X 0 1 2 4 5 q P 0.3 0.2 0.2 0.1 若离散型随机变量Y 满足Y 2X 1，则下列结果正确的有（ ） EX2 DX2.4 DX2.8 DY14 A． B． C． D． 【答案】AC 【解析】 由离散型随机变量X 的分布列的性质得： q 10.30.20.20.10.2 ， EX00.210.320.240.250.12 则 ，DX022 0.2122 0.3222 0.2422 0.2522 0.1 ， DX0.80.300.80.92.8 即 ， 因为离散型随机变量Y 满足Y 2X 1， DY22DY4DY42.811.2 . 故结果正确的有AC. 故选：AC. 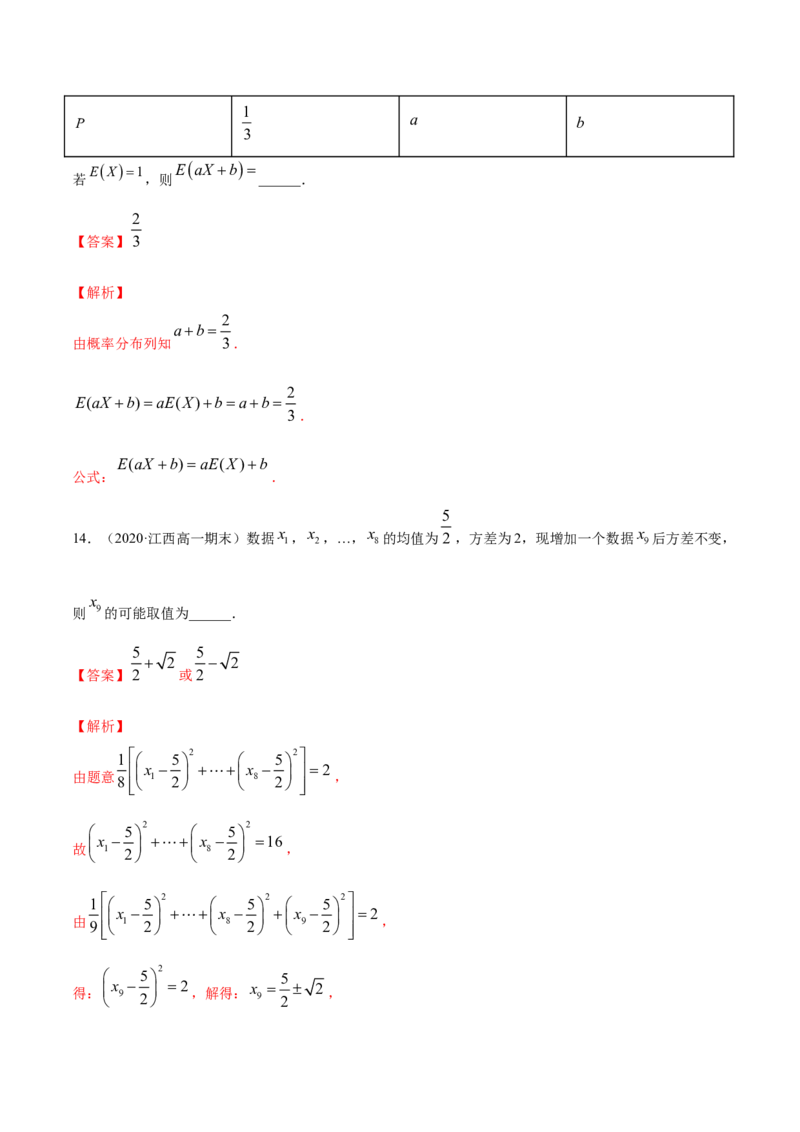0 p1  12．（2020·福建城厢莆田一中高二期中）（多选）设 ，随机变量 的分布列如下，则下列结论正 确的有（ ）  0 1 2 P p p2 p2 1 p E E p p A． 随着 的增大而增大 B． 随着 的增大而减小 P0 P2 P2 C． D． 的值最大 【答案】BC 【解析】 E p2 2(1 p)(p1)2 1 E 0 p1 p 由题意 ，由于 ，所以 随着 的增大而减小，A错，B正 确； 3 1 3 9 1 p P2 P1( )2   又 p p2  p(1 p)1 p，所以C正确； 4时， 4，而 4 16 4 ，D 错． 故选：BC． 三、填空题 13．（2020·黑龙江南岗哈师大附中高三其他（理））已知随机变量X 的分布列为 X 0 1 21 P a b 3 EX1 EaX b 若 ，则 ______． 2 【答案】3 【解析】 2 ab 由概率分布列知 3． 2 E(aX b)aE(X)bab 3 ． E(aX b)aE(X)b 公式： ． 5 x x x x 14．（2020·江西高一期末）数据 ， ，…， 的均值为2 ，方差为2，现增加一个数据 后方差不变， 1 2 8 9 x 则 9的可能取值为______． 5 5  2  2 【答案】2 或2 【解析】 1  5 2  5 2 由题意 8     x 1  2        x 8  2     2 ， 2 2  5  5 x    x  16 故  1 2      8 2   ， 1  5 2  5 2  5 2 由 9     x 1  2        x 8  2      x 9  2     2 ， 2  5 5 得：  x 9  2   2 ，解得： x 9  2  2 ，5 5  2  2 故答案为：2 或2 ． 15．（2020·重庆高三其他（理））甲、乙两人同时参加当地一个劳动实践活动，该活动有任务需要完成， 甲、乙完成任务的概率分别为0.7，0.8，且甲、乙是否完成任务相互独立互不影响.设这两人中完成任务的 总人数为X ，则EX ______. 3 【答案】1.5（或2 ） 【解析】 PX 010.810.70.06 X 的可能取值为0，1，2，且 ， PX 110.80.70.810.70.38 PX 20.80.70.56 ， ， EX 10.3820.561.5 故 . 3 故答案为：1.5（或2 ）. 1 1 0a 0b 16．（2020·浙江嵊州高三三模）已知 2， 2 ，随机变量X 的分布列是： X 0 1 2 1 P a b 2 2 EX 若 3，则a ________，DX________. 1 5 【答案】3 9 【解析】 1 ab 1  2  2  EXa2b  3  由题意可得 1 ，解得 1 ，  0a a   2  3   1 1 0b  b  2  6 2 2 2  2 1  2 1  2 1 5 DX 0   1   2   因此，       .  3 2  3 3  3 6 9 1 5 故答案为：3；9.、 四、解答题 17．（2019·全国高二课时练习）甲、乙两名射手在一次射击中得分为两个相互独立的随机变量ξ与η,且 ξ,η的分布列为 (1)求a,b的值. (2)计算ξ,η的均值与方差,并以此分析甲、乙的技术状况. a 0.3,b0.4 【答案】（1） ；（2）见解析 【解析】 (1)由离散型随机变量的分布列的性质可知a+0.1+0.6=1, 所以a=0.3. 同理0.3+b+0.3=1,b=0.4. (2)Eξ=1×0.3+2×0.1+3×0.6=2.3, Eη=1×0.3+2×0.4+3×0.3=2, Dξ=(1-2.3)2×0.3+(2-2.3)2×0.1+(3-2.3)2×0.6=0.81, Dη=(1-2)2×0.3+(2-2)2×0.4+(3-2)2×0.3=0.6. 由于Eξ>Eη,说明在一次射击中,甲的平均得分比乙高,但Dξ>Dη,说明甲得分的稳定性不如乙,因此甲、乙两人技术水平都不够全面,各有优势与劣势. P 0. 8 18．（2020·大连市普兰店区第一中学高二月考）某人投弹击中目标的概率为 . （1）求投弹一次，击中次数X 的均值和方差； 10 Y （2）求重复投弹 次，击中次数 的均值和方差. EX0.8 DX0.16 EY8 DY1.6 【答案】（1） ； （2） ， 【解析】 （1）由题意可知X 服从两点分布 P(X 0)0.2 P(X 1)0.8 因为， ， EX00.210.80.8 所以， . DX00.82 0.210.82 0.80.16 所以， Y B10,0.8 （2）由题意可知击中次数Y 服从二项分布，即 EYnp 100.88 所以， ， DY100.80.21.6 . 19．（2018·江西九江高二期末（理））某运动员射击一次所得环数X 的分布列如下： X 8 9 10 P 0．4 0．4 0．2  现进行两次射击，且两次射击互不影响，以该运动员两次射击中最高环数作为他的成绩，记为 ． （1）求该运动员两次命中的环数相同的概率；  E （2）求 的分布列和数学期望 ． 【答案】（1）0.36；（2）见解析，9.2 【解析】 P 0.40.40.16 （1）两次都命中8环的概率为 1P 0.40.40.16 两次都命中9环的概率为 2 P 0.20.20.04 两次都命中10环的概率为 3 设该运动员两次命中的环数相同的概率为P P P P P 0.160.160.040.36 1 2 3  （2） 的可能取值为8，9，10 P(8)0.40.40.16 ， P(9)20.40.40.40.40.48 ， P(10)1P(8)P(9)0.36 ，  的分布列为  8 9 10 P 0．16 0．48 0．36 E80.1690.48100.369.2 20．甲、乙两个同学同时报名参加某重点高校2010年自主招生，高考前自主招生的程序为审核材料和文化 测试，只有审核过关后才能参加文化测试，文化测试合格者即可获得自主招生入选资格．已知甲，乙两人 3 1 3 4 , , . 审核过关的概率分别为5 2 ，审核过关后，甲、乙两人文化测试合格的概率分别为4 5 （1）求甲，乙两人至少有一人通过审核的概率；   （2）设 表示甲，乙两人中获得自主招生入选资格的人数，求 的数学期望. 4 【答案】(1)甲，乙两人至少有一人通过审核的概率为5 ；17 (2)的数学期望为20 . 【解析】 (1)设A“甲，乙两人至少有一人通过审核”，则  3 1 4 pA1 1 1      5 2 5………………6分 0,1,2 (2)  3 3 1 4 33 p0 1  1       5 4 2 5 100 3 31 4 18 p2       5 42 5 100 49 p11  p0 p2  100  0 33 49 18 100 100 100 85 17 E0 p01 p12 p2  100 20…………12分 4 答：(1)甲，乙两人至少有一人通过审核的概率为5 ； 17 (2)的数学期望为20 . 1分 21.（2020·全国高三（理））在某次投篮测试中，有两种投篮方案：方案甲：先在A点投篮一次，以后都 3 在B点投篮；方案乙：始终在B点投篮.每次投篮之间相互独立.某选手在A点命中的概率为4 ，命中一次4 记3分，没有命中得0分；在B点命中的概率为5 ，命中一次记2分，没有命中得0分，用随机变量表  示该选手一次投篮测试的累计得分，如果 的值不低于3分，则认为其通过测试并停止投篮，否则继续投 篮，但一次测试最多投篮3次.  （1）若该选手选择方案甲，求测试结束后所得分 的分布列和数学期望. （2）试问该选手选择哪种方案通过测试的可能性较大？请说明理由. 【答案】（1）数学期望为3.05，分布列见解析（2）选择方案甲 【解析】 A A B B （1）在A点投篮命中记作 ,不中记作 ；在B点投篮命中记作 ,不中记作 ， 3 3 1 4 4 1 PA ,P  A  1  ,PB ,P  B  1  其中 4 4 4 5 5 5，  0,2,3,4 的所有可能取值为 ，则 1 1 1 1 P0 P  ABB   P  A  P  B  P  B      4 5 5 100 ， 1 1 4 8 P2 P  ABB  P  ABB  2    4 5 5 100， 3 75 P3 PA  4 100 ， 1 4 4 16 P4 P  ABB   P  A  PBPB    4 5 5 100． 1 2 3 4 P0 P2 P3 P4 的分布列为： 100 ， 25， 4， 25． 1 8 75 16 305 E0 2 3 4  3.05 所以 100 100 100 100 100 ， 3.05 所以， 的数学期望为 ． 75 16 91 P  P3   0.91 （2）选手选择方案甲通过测试的概率为 1 100 100 100 ， 选手选择方案乙通过测试的概率为 1 4 4 4 4 112 896 P  P3 2       0.896 2 5 5 5 5 5 125 1000 ， P  P 因为 2 1，所以该选手应选择方案甲通过测试的概率更大． 5 3 2 1 22．袋中有同样的球 个，其中 个红色， 个黄色，现从中随机且不返回地摸球，每次摸 个，当两种颜  色的球都被摸到时，即停止摸球，记随机变量 为此时已摸球的次数，求：.  (1)随机变量 的概率分布列；  (2)随机变量 的数学期望与方差. 5 9 【答案】(1)见解析；（2）2 ，20 . 【解析】 C1C1C1 3 P(2) 2 3 2  (1)随机变量可取的值为2,3,4． C1C1 5 5 4 A2C1 A2C1 3 A3C1 1 P(3) 2 3 3 2  P(4) 3 2  C1C1C1 10； C1C1C1C1 10 5 4 3 5 4 3 2  得随机变量 的概率分布列为： x 2 3 4 3 3 1 P x 5 10 103 3 1 5 E2 3 4  (2)随机变量  的数学期望为： 5 10 10 2； 5 3 5 3 5 1 9 D(2 )2 (3 )2 (4 )2  随机变量  的方差为： 2 5 2 10 2 10 20