专题37分类变量与列联表（解析版）_E015高中全科试卷_数学试题_选修3_05.专项训练_专题37分类变量与列联表

专题37 分类变量与列联表 一、单选题 1．（2020·陕西省商丹高新学校月考（文））下面是一个2×2列联表，则表中a，b的值分别为（ ） y y 合计 1 2 x a 21 73 1 x 2 25 27 2 合计 b 46 100 A．94，96 B．52，50 C．52，54 D．54，52 【答案】C 【解析】 a2173 a52 b46100 b54 由 ，得 ，由 ，得 ．故选C． 2．（2020·四川乐山·期末（理））为大力提倡“厉行节约，反对浪费”，某市通过随机询问100名性别不 同的居民是否能做到“光盘”行动，得到如下的列联表：（ ） 做不到“光盘” 能做到“光盘” 男 45 10 女 30 15 附： P（K2k） 0．10 0．05 0．025 k 2．706 3．841 5．024n(ad bc)2 K2  (ab)(cd)(ac)(bd) 参照附表，得到的正确结论是 A．在犯错误的概率不超过l％的前提下，认为“该市居民能否做到‘光盘’与性别有关” B．在犯错误的概率不超过l％的前提下，认为“该市居民能否做到‘光盘’与性别无关” C．有90％以上的把握认为“该市居民能否做到‘光盘’与性别有关” D．有90％以上的把握认为“该市居民能否做到‘光盘’与性别无关” 【答案】C 【解析】 100(45153010)2 K2= =3.03 由表计算得： 55457525 ，所以有90％以上的把握认为“该市居民能否做到‘光 盘’与性别有关”，选C． 22 K2 4.013 3．（2019·黄梅国际育才高级中学月考（文））若由一个 列联表中的数据计算得 ，那么 有（ ）把握认为两个变量有关系. 95% 97.5% 99% 99.9% A． B． C． D． 【答案】A 【解析】 K2 4.013 ∵一个2*2列联表中的数据计算得 ，且4.013＞3.841， ∴有95%的把握说这两个变量有关系. 故选：A 4．（2020·陕西临渭·期末（理））在对吸烟与患肺病这两个分类变量的计算中，下列说法正确的是（ ） 2 6.635 A．若 ，我们有99%的把握说明吸烟与患肺病有关，则某人吸烟，那么他99%可能患肺病. 2 B．若由随机变量 求出有99%的把握说吸烟与患肺病有关，则在100人中有99人患肺病.2 C．若由随机变量 求出有95%的把握说吸烟与患肺病有关，那么有5%的可能性使得推断错误. D．以上说法都不正确. 【答案】C 2 【解析】随机变量 求出有95%的把握说吸烟与患肺病有关，  有5%的可能性使得推断错误，认为吸烟与患肺病有关， 故选：C. 5．（2019·陕西省商丹高新学校开学考试（文））利用独立性检验来考查两个分类变量X 和Y 是否有关 X Y k 5.024 X Y 系时,通过查阅下表来确定“ 和 有关系”的可信度.如果 ,那么就有把握认为“ 和 有关 系”的百分比为 P(K2 k ) 0.15 0.10 0.05 0.025 0.010 0.005 0.001 0 k 2.072 2.706 3.841 5.024 6.635 7.879 10.828 0 25% 75% A． B． 2.5% 97.5% C． D． 【答案】D 【解析】因为k 5.024，而在观测值表中对应于5.024的是0.025，1-0.025=97.5%，所以有97.5%的 把握认为“X 和Y 有关系” ． 故选D． 6．（2020·河北枣强中学月考（文））为了调查高一学生在分班选科时是否选择物理科目与性别的关系， 随机调查100名高一学生，得到22列联表如下：由此得出的正确结论是( ) 选择物理 不选择物理 总计 男 35 20 55 女 15 30 45 总计 50 50 100nad bc2 K2  附： abcdacbd P  K2 k  0.050 0.010 0.001 0 k 3.841 6.635 10.828 0 A．在犯错误的概率不超过0.01的前提下，认为“选择物理与性别有关” B．在犯错误的概率不超过0.01的前提下，认为“选择物理与性别无关” 99.90 0 C．有 的把握认为“选择物理与性别有关” 99.90 0 D．有 的把握认为“选择物理与性别无关” 【答案】A nad bc2 K2  100(35302015)2 100 【解析】因为   ， abcdacbd 55455050 11 9.09 6.635 根据临界值表可知，能在犯错误的概率不超过0.01的前提下，认为“选择物理与性别有关”. 故选：A 7．（2020·辽宁葫芦岛·期末）2020年以来，为了抗击新冠肺炎疫情，教育部出台了“停课不停学”政策， 全国各地纷纷采取措施，通过网络进行教学，为莘莘学子搭建学习的平台.在线教育近几年蓬勃发展，为 学生家长带来了便利，节省了时间，提供了多样化选择，满足了不同需求，也有人预言未来的教育是互联 网教育.与此同时，网课也存在以下一些现象，自觉性不强的孩子网课学习的效果大打折扣，授课教师教 学管理的难度增大.基于以上现象，开学后某学校对本校课学习情况进行抽样调查，抽取25名女生，25名 男生进行测试、问卷等，调查结果形成以下2×2列联表，通过数据分析，认为认真参加网课与学生性别之 间（ ） 认真上网课 不认真上网课 合计 男生 5 20 25 女生 15 10 25 合计 20 30 50 参考数据：P  K2 k  0.05 0.01 0.001 0 k 3.841 6.635 10.828 0 A．有关的可靠性不足95% B．有99%的把握认为两者有关 C．有99.9%的把握认为两者有关 D．有5%的把握认为两者无关 【答案】B 5051015202 25 25 K2   6.635 10.828 【解析】由于 ，而 ，故有99%的把握认为两者有 20302525 3 3 关. 故选：B 8．（2014·江西高考真题（文））某人研究中学生的性别与成绩、视力、智商、阅读量这4个变量的关系， 随机抽查了52名中学生，得到统计数据如表1至表4，则与性别有关联的可能性最大的变量是（ ） 表1 成绩 不及格 及格 总计 性别 男 6 14 20 女 10 22 32 总计 16 36 52 表2 视力 好 差 总计 性别 男 4 16 20 女 12 20 32 总计 16 36 52 表3 智商 偏高 正常 总计性别 男 8 12 20 女 8 24 32 总计 16 36 52 表4 阅读量 丰富 不丰富 总计 性别 男 14 6 20 女 2 30 32 总计 16 36 52 A．成绩 B．视力 C．智商 D．阅读量 【答案】D nad bc2 K2  【解析】根据公式 分别计算得：A. abcdacbd 52(6221014)2 A:K2  0.009 16363220 ; 52(4201216)2 B:K2  1.769 16363220 ; 52(824812)2 C:K2  1.3 16363220 ; 52(143062)2 D:K2  23.48 16363220 选项D的值最大，所以与性别有关联的可能性最大,故选D. 二、多选题 9．（2020·枣庄市第三中学高二月考）某大学为了解学生对学校食堂服务的满意度，随机调查了50名男K2 生和50名女生，每位学生对食堂的服务给出满意或不满意的评价，得到如图所示的列联表.经计算 的 观测值k 4.762，则可以推断出（ ） 满意 不满意 男 30 20 女 40 10 P  K2 k  0.100 0.050 0.010 k 2.706 3.841 6.635 3 A．该学校男生对食堂服务满意的概率的估计值为5 B．调研结果显示，该学校男生比女生对食堂服务更满意 C．有95%的把握认为男、女生对该食堂服务的评价有差异 D．有99%的把握认为男、女生对该食堂服务的评价有差异 【答案】AC 【解析】 30 3 = 对于选项A,该学校男生对食堂服务满意的概率的估计值为30+20 5 ,故A正确； 40 4 3   对于选项B,该学校女生对食堂服务满意的概率的估计值为4010 5 5,故B错误； k 4.7623.841 95% 因为 ,所以有 的把握认为男、女生对该食堂服务的评价有差异,故C正确,D错误 故选：AC 10．（2020·江苏省丰县中学期末）某俱乐部为了解会员对运动场所的满意程度，随机调查了50名会员， K2 每位会员对俱乐部提供的场所给出满意或不满意的评价，得到如图所示的列联表，经计算 的观测值 k 5.059，则可以推断出（ ）满意 不满意 总计 男生 18 9 27 女生 8 15 23 总计 26 24 50 附： P  K2 k  0.025 0.010 0.005 0 k 5.024 6.635 7.879 0 2 A．该俱乐部的男性会员对运动场所满意的概率的估计值为3 ； B．调查结果显示，该俱乐部的男性会员比女性会员对俱乐部的场所更满意； 97.5% C．有 的把握认为男性会员、女性会员对运动场所的评价有差异； 99% D．有 的把握认为男性会员、女性会员对运动场所的评价有差异. 【答案】ABC 18 2  【解析】对于选项A，该学校男生对运动场所满意的概率的估计值为27 3 ，故A正确； 8 对于选项B，该学校女生对运动场所满意的概率的估计值为23， 2 46 8 24    而3 69 23 69 ，故B正确； k 5.0595.024 97.5% 因为 ，有 的把握认为男性会员、女性会员对运动场所的评价有差异，故C正确， D错误. 故选：ABC. 11．（2020·山东济南·高二期末）在一次恶劣气候的飞行航程中，调查男女乘客在机上晕机的情况，如下表所示： 晕机 不晕机 合计 男 n 15 n 11 1 女 6 n n 22 2 合计 n 28 46 1 则下列说法正确的是（ ） nad bc2 2  附：参考公式： ，其中 . acbdabcd nabcd 独立性检验临界值表 P  K2 k  0.10 0.05 0.025 0.010 0 k 2.706 3.841 5.024 6.635 0 n 6 11  A．n n 1 2 2 2.706 B． 90% C．有 的把握认为，在恶劣气候飞行中，晕机与否跟男女性别有关 D．没有理由认为，在恶劣气候飞行中，晕机与否跟男女性别有关 【答案】ABD 【解析】由列联表数据，知 n 6n 11 1  15n 28 n 12  22 11   n 15n n 13 11 1  22    6n 22 n 2 ，得n 1 18 n 2846  n 27  1  1  n n 46   n 19 1 2 2n 12 4 6 6 11     ∴n 27 9 n 19 ，即A正确 1 2 晕机 不晕机 合计 男 12 15 27 女 6 13 19 合计 18 28 46 46(1213615)2 2  0.775 ∴ 18281927 < 2.706，即B正确 且没有理由认为，在恶劣气候飞行中，晕机与否跟男女性别有关；即D正确 故选：ABD 12．（2020·烟台市教育科学研究院高三其他）某校计划在课外活动中新増攀岩项目，为了解学生喜欢攀岩 和性别是否有关，面向学生开展了一次随机调查，其中参加调查的男女生人数相同，并绘制如下等高条形 图，则（ ） n(ad bc)2 K2  参考公式： (ab)(cd)(ac)(bd) ， nabcd . P  K2 k  0.05 0.01 0 k 3.841 6.635 0 A．参与调查的学生中喜欢攀岩的男生人数比喜欢攀岩的女生人数多 B．参与调查的女生中喜欢攀岩的人数比不喜欢攀岩的人数多C．若参与调查的男女生人数均为100人，则有99%的把握认为喜欢攀岩和性别有关 D．无论参与调查的男女生人数为多少，都有99%的把握认为喜欢攀岩和性别有关 【答案】AC m 【解析】由题意设参加调查的男女生人数均为 人，则 喜欢攀岩 不喜欢攀岩 合计 男生 0.8m 0.2m m 女生 0.3m 0.7m m 合计 1.1m 0.9m 2m 所以参与调查的学生中喜欢攀岩的男生人数比喜欢攀岩的女生人数多，A对B错； 2m(0.56m2 0.06m2)2 50m K2   1.1m0.9mmm 99 ， 50m 50100 K2   50.5056.635 当m100时， 99 99 ， 所以当参与调查的男女生人数均为100人，则有99%的把握认为喜欢攀岩和性别有关，C对D错， 故选：AC 三、填空题 16．（2020·湖南高二月考）在西非肆虐的“埃博拉病毒”的传播速度很快，这已经成为全球性的威胁，为 了考察某种埃博拉病毒疫苗的效果，现随机抽取100只小鼠进行试验，得到如下联表： 感染 未感染 总计 服用 10 40 50 未服用 20 30 50 总计 30 70 100 nad bc2 K2  参考公式： abcdacbd 0.15 0.10 0.05 0.025 0.010 0.005 0.001k 2.072 2.706 3.841 5.024 6.635 7.879 10.828 参照附表，在犯错误的概率最多不超过__________（填百分比）的前提下，可认为“该种疫苗由预防埃博 拉病毒感染的效果”． 【答案】5% 100103020402 K2  4.7623.841 【解析】由题意可得， ，参照附表，可得：在犯错误的概 50503070 50 50 0 0 率不超过 的前提下，认为“小动物是否被感染与有没有服用疫苗有关”，故答案为 . 方法点睛：独立性检验的一般步骤：（1）根据样本数据制成22列联表；（2）根据公式 nad bc2 K2  计算 的值；(3) 查表比较 与临界值的大小关系，作统计判断. abadacbd K2 K2 （注意：在实际问题中，独立性检验的结论也仅仅是一种数学关系，得到的结论也可能犯错误. 14．（2020·西安市长安区第五中学月考（文））下面是一个22列联表: y y 总计 1 2 x 35 a 70 1 x 15 15 30 2 总计 50 b 100 a,b 其中 处填的值分别为________________． 【答案】35，50 【解析】由a3570，得a 35， a15b b50 ，得 . 35 50 故答案为： ， .X,Y K2 15．（2020·安徽黄山·高二期末（文））已知变量 ，由它们的样本数据计算得到 的观测值 k 4.328 K2 ， 的部分临界值表如下： X,Y 则最大有________的把握说变量 有关系.（填百分数） 【答案】95% 【解析】 K2 k 4.328>3.841 X,Y 因为 的观测值 ，所以在犯错误的概率不超过0.05的前提下认为变量 有关系. 95% X,Y 所以最大有 的把握说变量 有关系. 95% 故答案为： . 16．（2018·全国高二单元测试）某高校“统计初步”课程的教师随机调查了选该课的一些学生情况，具 体数据如下表： 专业 非统计专业 统计专业 性别 男 13 10 女 7 20 为了判断主修统计专业是否与性别有关系，根据表中的数据，计算得到K2＝________(保留三位小数)，所 以判定________(填“能”或“不能”)在犯错误的概率不超过0.05的前提下认为主修统计专业与性别有关 系． 【答案】4.844 能 【解析】 50(1320710)2 K2  4.8443.841 根据提供的表格得 23272030 . ∴所以可以在犯错误的概率不超过0.05的前提下认为主修统计专业与性别有关系．4.844 故答案为（1） ；（2）能. 四、解答题 17．（2020·青海西宁·期末（文））某大学的一个社会实践调查小组，在对大学生就餐“光盘习惯”的调 查中，随机发放了120份调查问卷．对收回的100份有效问卷进行统计，得到如下22列联表： 做不到光盘 能做到光盘 合计 男 45 10 55 女 x y 45 合计 75 m 100 （1）求表中x，y的值； （2）若在犯错误的概率不超过P的前提下认为良好“光盘习惯”与性别有关，那么根据临界值表，最精确的 P的值应为多少？请说明理由． n(ad bc)2 K2  附：独立性检验统计量 (ab)(cd)(ac)(bd) ，其中 nabcd ． P  K2 k  0.25 0.15 0.10 0.05 0.025 0 k 1.323 2.072 2.706 3.840 5.024 0 x30,y 15 P0.1 【答案】（1） ；（2） ；理由见解析. 【解析】 45x75 x30   75m100 y 15 （1）由题意可知： ，解得： ，   10 y m m25   x30,y 15 ∴ ， n(ad bc)2 100(45153010)2 K2   3.03 （2） (ab)(cd)(ac)(bd) 55457525 ， 2.7063.033.840， P0.1 所以能在犯错误的概率不超过0.10的前提下认为良好“光盘习惯”与性别有关，即 ． 18．（2020·全国高考真题（文））某学生兴趣小组随机调查了某市100天中每天的空气质量等级和当天到某公园锻炼的人次，整理数据得到下表（单位：天）： 锻炼人次 [0，200] (200，400] (400，600] 空气质量等级 1（优） 2 16 25 2（良） 5 10 12 3（轻度污染） 6 7 8 4（中度污染） 7 2 0 （1）分别估计该市一天的空气质量等级为1，2，3，4的概率； （2）求一天中到该公园锻炼的平均人次的估计值（同一组中的数据用该组区间的中点值为代表）； （3）若某天的空气质量等级为1或2，则称这天“空气质量好”；若某天的空气质量等级为3或4，则称这 天“空气质量不好”．根据所给数据，完成下面的2×2列联表，并根据列联表，判断是否有95%的把握认为 一天中到该公园锻炼的人次与该市当天的空气质量有关？ 人次≤400 人次>400 空气质量好 空气质量不好 n(ad bc)2 K2  附： (ab)(cd)(ac)(bd) ， P(K2≥k) 0.050 0.010 0.001 k 3.841 6.635 10.828 1 2 3 4 0.43 0.27 0.21 0.09 【答案】（1）该市一天的空气质量等级分别为 、 、 、 的概率分别为 、 、 、 ； 350 （2） ；（3）有，理由见解析. 【解析】 21625 0.43 （1）由频数分布表可知，该市一天的空气质量等级为1的概率为 100 ，等级为2的概率为51012 678 720 0.27 0.21 0.09 100 ，等级为3的概率为 100 ，等级为4的概率为 100 ； 100203003550045 350 （2）由频数分布表可知，一天中到该公园锻炼的人次的平均数为 100 （3）22列联表如下： 人次400 人次400 空气质量不好 33 37 空气质量好 22 8 10033837222 K2  5.8203.841 ， 55457030 95% 因此，有 的把握认为一天中到该公园锻炼的人次与该市当天的空气质量有关. 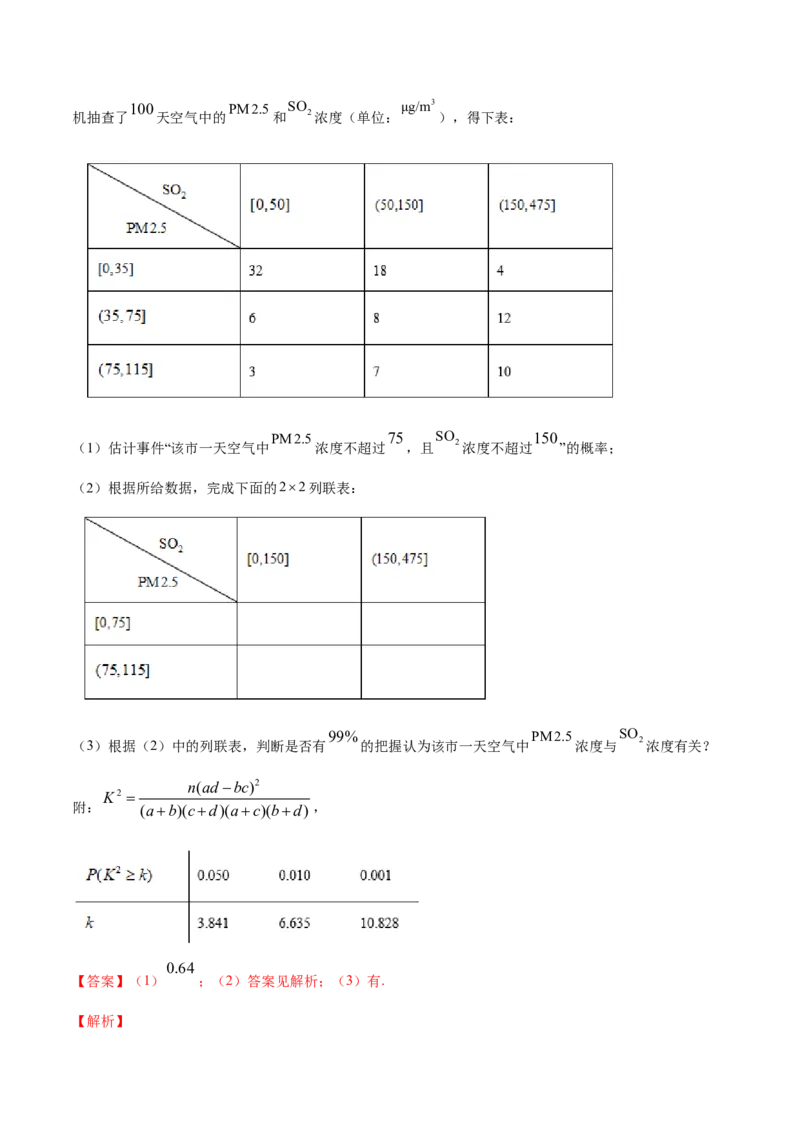19．（2020·河南开封·期末（文））为加强环境保护，治理空气污染，环境监测部门对某市空气质量进 100 PM2.5 SO μg/m3 行调研，随机抽查了 天空气中的 和 2浓度（单位： ），得下表： SO 2 [0,50] (50,150] (150,475] PM2.5 [0,35] 32 18 4 (35,75] 6 8 12 (75,115] 3 7 10 PM2.5 75 SO 150 （1）估计事件“该市一天空气中 浓度不超过 ，且 2浓度不超过 ”的概率； （2）根据所给数据，完成下面的22列联表： SO 2 [0,150] (150,475] PM2.5 [0,75](75,115] 99% PM2.5 SO （3）根据（2）中的列联表，判断是否有 的把握认为该市一天空气中 浓度与 2浓度有关？ n(ad bc)2 K2  附： (ab)(cd)(ac)(bd) ， P(K2 k) 0.050 0.010 0.001 k 3.841 6.635 10.828 0.64 【答案】（1） ；（2）答案见解析；（3）有. 【解析】 SO PM2.5 （1）由表格可知，该市100天中，空气中的 浓度不超过75，且 2浓度不超过150的天数有 32618864天， 64 0.64 SO 所以该市一天中，空气中的PM2.5浓度不超过75，且 浓度不超过150的概率为100 ； 2 （2）由所给数据，可得22列联表为： SO 2 0,150 150,475 合计 PM2.5 0,75 64 16 80 75,115 10 10 20 合计 74 26 100 （3）根据22列联表中的数据可得 n(ad bc)2 100(64101610)2 3600 K2    7.48446.635 (ab)(cd)(ac)(bd) 80207426 481 ， SO 99% PM2.5 因为根据临界值表可知，有 的把握认为该市一天空气中 浓度与 2浓度有关. 20．（2020·海南高考真题）为加强环境保护，治理空气污染，环境监测部门对某市空气质量进行调研，随100 PM2.5 SO μg/m3 机抽查了 天空气中的 和 2浓度（单位： ），得下表： PM2.5 75 SO 150 （1）估计事件“该市一天空气中 浓度不超过 ，且 2浓度不超过 ”的概率； （2）根据所给数据，完成下面的22列联表： 99% PM2.5 SO （3）根据（2）中的列联表，判断是否有 的把握认为该市一天空气中 浓度与 2浓度有关？ n(ad bc)2 K2  附： (ab)(cd)(ac)(bd) ， 0.64 【答案】（1） ；（2）答案见解析；（3）有. 【解析】SO PM2.5 （1）由表格可知，该市100天中，空气中的 浓度不超过75，且 2浓度不超过150的天数有 32618864天， 64 0.64 SO 所以该市一天中，空气中的PM2.5浓度不超过75，且 浓度不超过150的概率为100 ； 2 （2）由所给数据，可得22列联表为： SO 2 0,150 150,475 合计 PM2.5 0,75 64 16 80 75,115 10 10 20 合计 74 26 100 （3）根据22列联表中的数据可得 n(ad bc)2 100(64101610)2 3600 K2    7.48446.635 (ab)(cd)(ac)(bd) 80207426 481 ， SO 99% PM2.5 因为根据临界值表可知，有 的把握认为该市一天空气中 浓度与 2浓度有关. 21．（2020·福建三元·三明一中其他（文））为研制新冠肺炎的疫苗，某生物制品研究所将所研制的某 型号疫苗用在小白鼠身上进行科研和临床试验，得到如下统计数据： 未感染病毒 感染病毒 总计 未注射疫苗 40 p x 注射疫苗 60 q y 总计 100 100 200 3 现从未注射疫苗的小白鼠中任取1只，取到“感染病毒”的小白鼠的概率为5． （1）能否有99.5%的把握认为注射此疫苗有效？5 5 （2）在感染病毒的小白鼠中，按未注射疫苗和注射疫苗的比例抽取 只进行病理分析，然后从这 只小白 鼠中随机抽取3只对注射疫苗的情况进行核实，求恰有1只为注射过疫苗的概率． nad bc2 K2  附： ， . abcdacbd nabcd P  K2 k  0.05 0.01 0.005 0.001 0 k 3.841 6.635 7.879 10.828 0 3 【答案】（1）有99.5%的把握认为注射此疫苗有效；（2）5. 【解析】 p 3  （1）依题意，由40 p 5 ，得 p 60，所以q 40，x y 100， 所以，22列联表如下表所示： 未感染病毒 感染病毒 总计 未注射疫苗 40 60 100 注射疫苗 60 40 100 总计 100 100 200 200404060602 K2  87.879 由 ，所以有 的把握认为注射此疫苗有效； 100100100100 99.5% （2）设“恰有1只为注射过疫苗”为事件A， 60 3  由于在感染病毒的小白鼠中，按未注射疫苗和注射疫苗的比例40 2 抽取， 故抽取的5只小白鼠中有3只未注射疫苗，分别用1、2、3来表示，2只已注射疫苗的小白鼠分别用a、 b来表示， 1,2,3 1,2,a 1,2,b 1,3,a 1,3,b 5 3 从这 只小白鼠中随机抽取 只，可能的情况有： 、 、 、 、 、1,a,b 2,3,a 2,3,b 2,a,b 3,a,b 10 、 、 、 、 ，共 种， 1,2,a 1,2,b 1,3,a 1,3,b 2,3,a 2,3,b 其中恰有1只为注射过疫苗有： 、 、 、 、 、 ，共 6 种， 6 3 3 PA  所以 10 5，即恰有1只为注射过疫苗的概率为5． 22．（2020·四川泸州·期末（理））高二理科班有60名同学参加某次考试，从中随机抽选出5名同学， 他们的数学成绩x与物理成绩 y 如下表： x 数学成绩 140 130 120 110 100 y 物理成绩 110 90 100 80 70 数据表明 y 与x之间有较强的线性关系. （Ⅰ）求 y 关于x的线性回归方程，并估计该班某同学的数学成绩为90分时该同学的物理成绩； （Ⅱ）本次考试中，规定数学成绩达到125分为数学优秀，物理成绩达到100分为物理优秀.若该班数学优 秀率与物理优秀率分别为50%和60%，且所有同学中数学优秀但物理不优秀的同学共有6人，请你在答卷页 上填写下面22列联表，并判断能否在犯错误的概率不超过0.01的前提下认为数学优秀与物理优秀有关？ 物理优秀 物理不优秀 合计 数学优秀 数学不优秀 合计 n n x y nxy  x x  y  y  i i i i b ˆ  i1  i1 参考公式及数据：回归直线的系数  n x2 nx 2  n  x x 2 ， ， i i aˆ  yb ˆ x i1 i1  n x i y i 54900，  5  x i x 2 1000， K2  abc n  a d d   a bc   c 2 bd . P  K2 6.635  0.01 ， i1 i1 P  K2 10.828  0.001 .yˆ 0.9x18 【答案】（Ⅰ） ，估计该班某同学的数学成绩为90分时该同学的物理成绩为63分；（Ⅱ）能 在犯错误的概率不超过0.01的前提下认为数学优秀与物理优秀有关． 【解析】 1 （Ⅰ）x (140130120110100)120， 5 1 y (110901008070)90． 5 5 (x x)(y  y) i i 2020100010(10)(10)(20)(20) 900 b ˆ  i1   0.9， 5 202 102 (10)2 (20)2 1000 (x x)2 i i1 aˆ yb ˆ x900.912018 ． y x yˆ 0.9x18 关于 的线性回归方程为 ， x90 yˆ 0.9901863 取 ，得 ．  估计该班某同学的数学成绩为90分时该同学的物理成绩为63分； （Ⅱ）由题意填写22列联表： 物理优秀 物理不优秀 合计 数学优秀 24 6 30 数学不优秀 12 18 30 合计 36 24 60 60(2418612)2 K2  106.635， 36243030  能在犯错误的概率不超过0.01的前提下认为数学优秀与物理优秀有关．