文档内容
第六章 平面向量及其应用 单元测试卷
学校:___________姓名:___________班级:___________考号:___________
一、选择题(共40分)
1、(4分)已知D是 所在平面内的一点,且 ,设 ,则
( ).
A. B. C.3 D.-3
2、(4分)在菱形ABCD中, , , ,P是菱形ABCD内
部及边界上一点,则 的最大值是( )
A. B. C.13 D.
3、(4分)已知点O为 所在平面上一点,且满足 ,若 的面积
与 的面积比值为 ,则 的值为( )
A. B. C.2 D.3
4、(4分)费马点是指三角形内到三角形三个顶点距离之和最小的点,当三角形三个内角均小
时,费马点与三个顶点连线正好三等分费马点所在的周角,即该点所对三角形三边的张角相等,
均为 .根据以上性质,已知 ,P为 内一点,记
,则 的最小值为( )
A. B. C. D.
5、(4分)已知向量a,b满足 , , ,则a与b的夹角为( ).
A. B. C. D.
6、(4分)已知在直角梯形ABCD中, , , , ,P是DC的
中点,则 ( ).
A. B. C.3 D.9
7、(4分)已知 ,向量a与向量b的夹角为120°,e是与b同向的单位向量,则a在b上的投影
向量为( ).
A.e B. C. D.8、(4分)已知对任意的平面向量 ,把 绕其起点A沿逆时针方向旋转 角得到向量
,叫作把点B绕点A沿逆时针方向旋转 角得到点P.已知
, ,把点B绕点A沿逆时针方向旋转 得到点P,则点P的坐标为( ).
A. B. C. D.
9、(4分)若平面向量a与b的夹角为60°, , ,则 等于( ).
A. B. C.4 D.12
10、(4分)已知向量 , ,若 ,则实数x等于( ).
A.4 B.5 C.6 D.7
二、填空题(共25分)
11、(5分)在 中, 为 上两点且 ,若 ,则 的长
为_____________.
12、(5分)若 ,且满足 , , ,则 __________.
13、(5分)已知在梯形ABCD中, , , , ,若EF在线段AB
上运动,且 ,则 的最小值为____________.
14、(5分)已知 , ,若 , ,则点C的坐标_________.
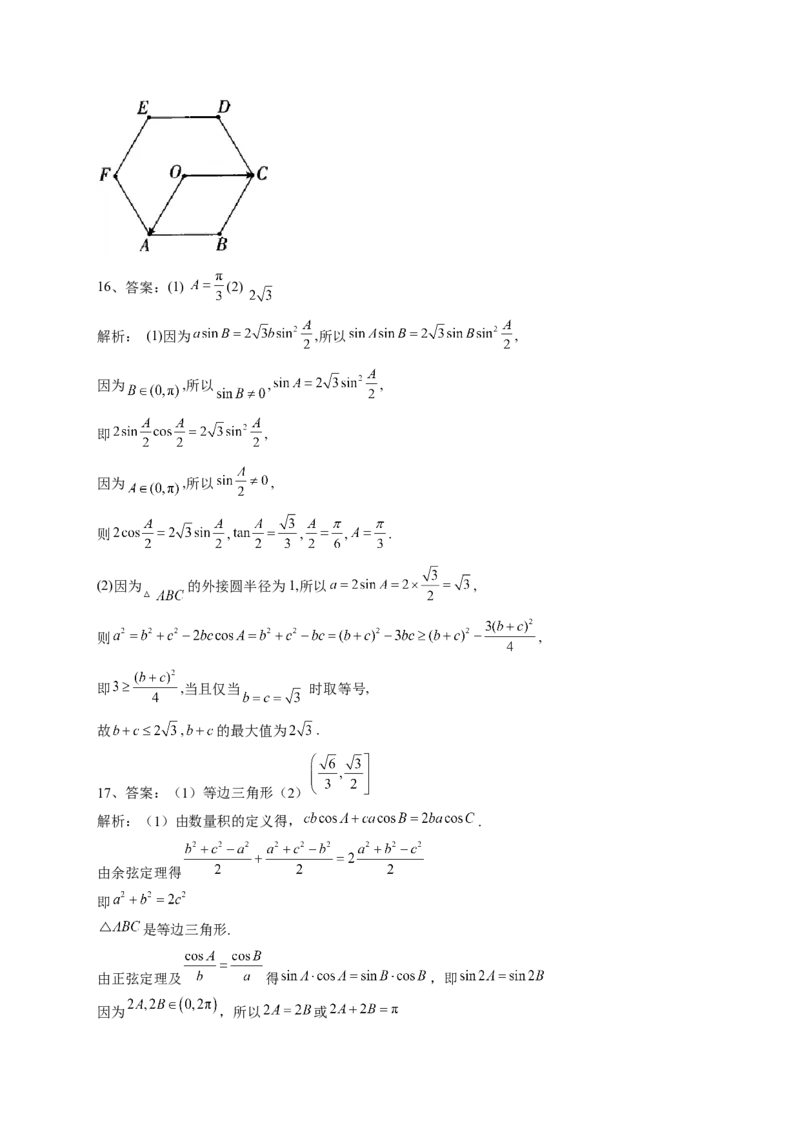
15、(5分)已知中心为O的正六边形ABCDEF的边长为2,则 _____________.
三、解答题(共35分)
16、(8分)已知 的内角 所对的边为 ,且满足 .
(1)求角 的大小;
(2)若 的外接圆半径为1,求 的最大值.
17、(9分)已知 的三个内角 的对边分别为 ,且
(1)若 ,判断 的形状并说明理由;
(2)若 是锐角三角形,求 的取值范围
18、(9分) 的内角 的对边分别为 ,已知 .
(1)求B;
(2)若 , 的面积为 ,求 的周长.
19、(9分)在 中,内角 的对边分别为 的面积S满足
(1)求 ;(2)若 为锐角三角形, ,求 的取值范围.参考答案
1、答案:D
解析:由题意作图,如图所示,因为 ,所以C为BD的中点,
所以 ,因为 ,
所以由平面向量基本定理可得 , ,所以 ,故选D.
2、答案:B
解析:
3、答案:B
解析:
4、答案:B
解析:设 为坐标原点,由 , , ,知 且 为锐角
三角形,因此,费马点M在线段OC上,设 ,如图,
则 为顶角是120°的等腰三角形,故 ,所以
,则 的最小值为 .故选:B.
5、答案:C
解析: , , , ,
, .故选C.
6、答案:C解析:因为 , ,所以
,故选C.
7、答案:D
解析:a在b上的投影向量为 .故选D.
8、答案:D
解析:由已知可得 ,
将点 绕点A沿逆时针方向旋转 ,
得 .
, ,故选D.
9、答案:B
解析:因为 ,所以 ,又因为向量a与b的夹角为60°, ,
所以 ,所以 .
10、答案:C
解析:由题意可得 ,解得 .故选C.
11、答案:
解析:由题意,在 中,由余弦定理得 ;在 中,由余弦定理得
.又 ,即
.又 ,.易知 .在 中,由余弦定理得
, .
12、答案:略
解析:
13、答案:
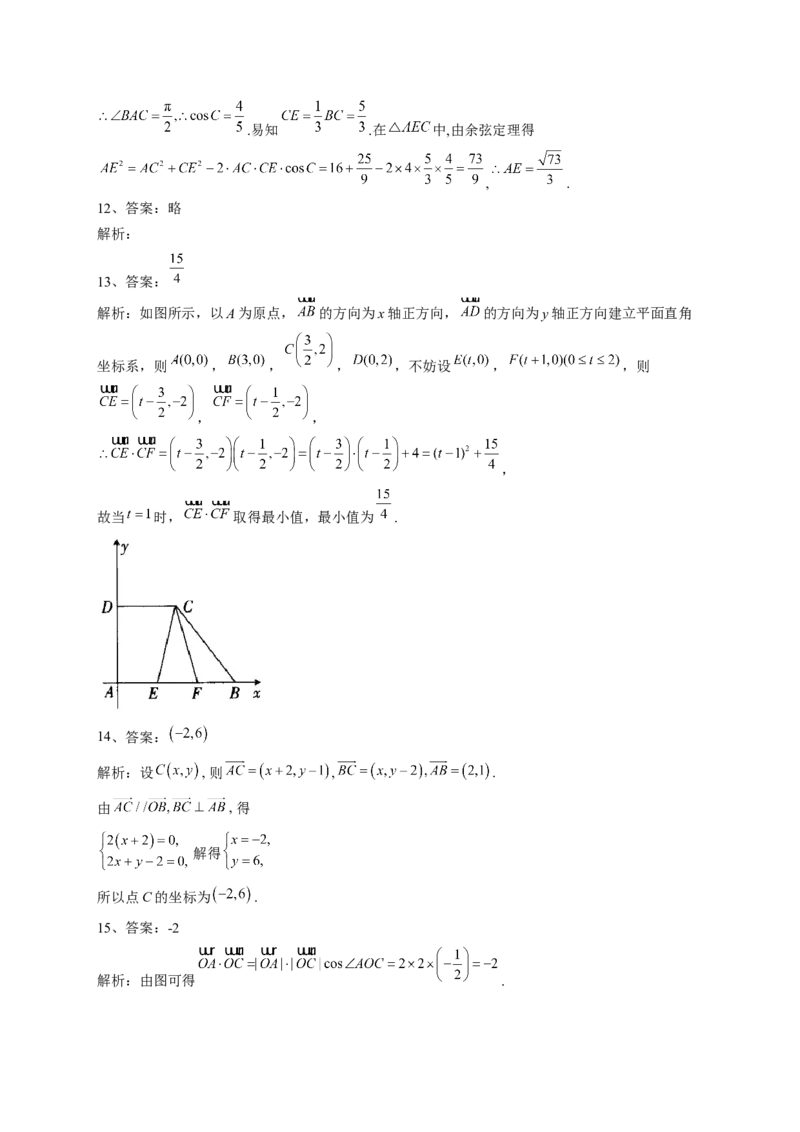
解析:如图所示,以A为原点, 的方向为x轴正方向, 的方向为y轴正方向建立平面直角
坐标系,则 , , , ,不妨设 , ,则
, ,
,
故当 时, 取得最小值,最小值为 .
14、答案:
解析:设 , 则 , .
由 , 得
解得
所以点C的坐标为 .
15、答案:-2
解析:由图可得 .16、答案:(1) (2)
解析: (1)因为 ,所以 ,
因为 ,所以 , ,
即 ,
因为 ,所以 ,
则 , , , .
(2)因为 的外接圆半径为1,所以 ,
则 ,
即 ,当且仅当 时取等号,
故 , 的最大值为 .
17、答案:(1)等边三角形(2)
解析:(1)由数量积的定义得, .
由余弦定理得
即
是等边三角形.
由正弦定理及 得 ,即
因为 ,所以 或当 时, 是等腰三角形,此时 ,所以 是等边三角形;
当 ,即 时, 是直角三角形,这与 矛盾.
故 是等边三角形.
(2)不妨设 ,由 得 ,
于是
又因为 是锐角三角形、所以 ,
即 ,因此
由余弦定理得,
令 ,则 ,函数 在 上单调递增.
所以 ,因此
的取值范围是
故
18、答案:(1) (2)
解析: (1) ,
由正弦定理得: ,
整理得: ,
∵在 中, ,∴ ,
即 ,∴ ,即 ;
(2)由余弦定理得: ,∴ ,
∵ ,
∴ ,∴ ,∴ ,
∴ 的周长为 .
19、答案: (1) (2)解析: (1)由题得
(2)由正弦定理得 ,
为锐角三角形, , ,
,
的取值范围是