文档内容
第十章 概率 单元测试卷
学校:___________姓名:___________班级:___________考号:___________
一、选择题(共40分)
1、(4分)某高校有智能餐厅 、人工餐厅 ,甲第一天随机地选择一餐厅用餐,如果第一天去
餐厅,那么第二天去 餐厅的概率为0.6;如果第一天去 餐厅,那么第二天去 餐厅的概率为
0.8.则甲第二天去 餐厅用餐的概率为( )
A. 0.75 B. 0.7 C. 0.56 D. 0.38
2、(4分)同时投掷两个质地均匀的骰子,两个骰子的点数至少有一个是奇数的概率为( )
A. B. C. D.
3、(4分)有4张卡片,上面分别写有数字1,2,3,4,从这4张卡片中随机抽取2张,则取出的2
张卡片上的数字之和为偶数的概率为( )
A. B. C. D.
4、(4分)某学生参与一种答题游戏, 需要从 三道试题中选出一道进行回答, 回答正确即可获
得奖品. 若该 学生选择 的概率分别为0.3,0.4,0.3, 答对 的概率分别为0.4,0.5,0.6, 则
其获得奖品的 概率为( )
A. 0.5 B. 0.55 C. 0.6 D. 0.75
5、(4分)甲乙两人在数独APP上进行“对战赛”,每局两人同时解一道题,先解出题 的人赢得一
局,假设无平局,且每局甲乙两人赢的概率相同,先赢3局者获胜,则甲获胜且比赛恰进行了4局
的概率是( )
A. B. C. D.
6、(4分)一个人连续射击三次,事件“至少有一次击中目标”的对立事件是( )
A.至多有一次击中目标 B.三次都击不中目标
C.三次都击中目标 D.只有一次击中目标
7、(4分)从某高中2021名学生中选取50名学生参加数学竞赛,若采用以下方法选取:先用简单随
机抽样方法从2021名学生中剔除21名,再从余下的2000名学生中随机抽取50名.则其中学生丙
被选取和被剔除的概率分别是( )
A. , B. , C. , D. ,
8、(4分)一个人打靶时连续射击两次,事件“两次都不中靶”的对立事件是( )
A.至多有一次中靶 B.两次都中靶
C.只有一次中靶 D.至少有一次中靶
9、(4分)同时掷3枚硬币,那么互为对立事件的是( )
A.至少有1枚正面和最多有1枚正面 B.最多1枚正面和恰有2枚正面C.至多1枚正面和至少有2枚正面 D.至少有2枚正面和恰有1枚正面
10、(4分)甲、乙两人参加“社会主义价值观”知识竞赛,甲、乙两人能荣获一等奖的概率分别为
和 ,甲、乙两人是否获得一等奖相互独立,则这两个人中恰有一人获得一等奖的概率为( )
A. B. C. D.
二、填空题(共25分)
11、(5分)从红、绿、黄、紫、白、蓝 6 种颜色中任选 2 种不同的颜色, 则没有选红色的概率为
____________.
12、(5分)一颗标有数字 的骰子连续郑两次,朝上的点数依次记为 ,使得复数
为实数的概率是____________.
13、(5分)天气预报元旦假期甲地降雨的概率是0.2,乙地降雨的概率是0.3,假定在这段时间内两
地之间是否降雨相互之间没有影响,则这两地中恰有一个地方降雨的概率为____________.
14、(5分)从集合 中任取两个不同的数 , 则 的概率为_______________.
15、(5分)某学校团委在2021年春节前夕举办教师“学习强国”知识答题赛,其中高一年级的甲、
乙两名教师组队参加答题赛,比赛共分两轮,每轮比赛甲、乙两人各答一题.已知甲答对每个题
的概率为 ,乙答对每个题的概率为 .假定甲、乙两人答题正确与否互不影响,则比赛结束时,
甲、乙两人共答对三个题的概率为____________.
三、解答题(共35分)
16、(8分)一个袋中装有四个形状、大小完全相同的球,球的编号分别为1,2,3,4.
(1)从袋中随机取两个球,求取出的球的编号之和不大于4的概率.
(2)先从袋中随机取一个球,该球的编号为m,将球放回袋中,然后再从袋中随机取一个球,该球
的编号为n,求 的概率.
17、(9分)某连锁超市旗舰店在元旦当天推出一个购物满百元抽奖活动,凡是一次性购物满百元者
可以从抽奖箱中一次性任意摸出2个小球(抽奖箱内共有5个小球,每个小球大小形状完全相同,
这5个小球上分别标有1,2,3,4,5 这5个数字).
(1)列出摸出的2个小球的所有可能的结果.
(2)已知该超市活动规定:摸出的2个小球都是偶数为一等奖;摸出的2个小球都是奇数为二等
奖.请分别求获得一等奖的概率与获得二等奖的概率.
18、(9分)一汽车厂生产A,B,C三类轿车,每类轿车均有舒适型和标准型两种型号,某月的产量
(单位:辆)如下表:
轿车A 轿车B 轿车C
舒适型 100 150 z标准型 300 450 600
按类用分层抽样的方法在这个月生产的轿车中抽取50辆,其中有A类轿车10辆.
(1)求z的值.
(2)用分层抽样的方法在C类轿车中抽取一个容量为5的样本.将该样本看成一个总体,从中任取2
辆,求至少有1辆舒适型轿车的概率.
(3)用随机抽样的方法从B类舒适型轿车中抽取8辆,经检测它们的得分为:9.4,8.6,9.2,9.6,
8.7,9.3,9.0,8.2.把这8辆轿车的得分看成一个总体,从中任取一个数,求该数与样本平均数之
差的绝对值不超过0.5的概率.
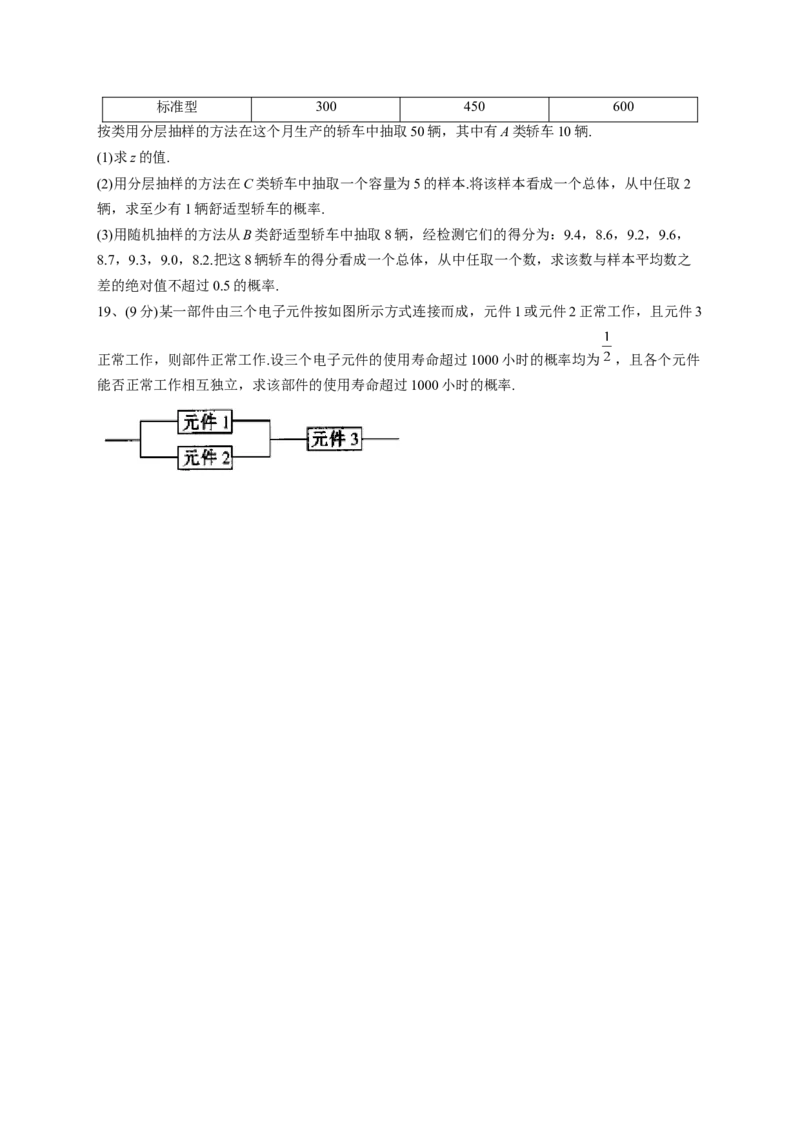
19、(9分)某一部件由三个电子元件按如图所示方式连接而成,元件1或元件2正常工作,且元件3
正常工作,则部件正常工作.设三个电子元件的使用寿命超过1000小时的概率均为 ,且各个元件
能否正常工作相互独立,求该部件的使用寿命超过1000小时的概率.参考答案
1、答案:A
解析:
2、答案:D
解析:一共有 种情况,两个均为偶数共有 种,故至少有一个奇数的概率
3、答案:C
解析:略
4、答案:A
解析:该学生获得奖品的概率为 .
5、答案:D
解析:
6、答案:B
解析:一个人连续射击三次事件“至少有一次击中目标”的对立事件是“三次都击不中目标”.故
选B.
7、答案:B
解析:由已知丙被剔除的概率是 ,那么丙不被剔除的概率是 ,只有
在丙不被剔除的情况下,丙才可能被抽取,因此概率为 .故选:B.
8、答案:D
解析:一个人打靶时连续射击两次,
事件“两次都不中靶”的对立事件是:至少有一次中靶。
故答案为:D
9、答案:C
解析:由题意知,至少有一枚正面包括有一正两反,两正一反,三正,三种情况
最多有一枚正面包括一正两反,三反,两种情况,故A不正确
最多有一枚正面包括一正两反,三反,与恰有2枚正面是互斥的但不是对立事件,故B不正确
不多于一枚正面包括一正两反,三反,至少有2枚正面包括2正一反和三正,故C正确
至少有2枚正面包括2正一反和三正,与恰有1枚正面是互斥但不对立事件,故D不正确
故选C
10、答案:D解析:根据题意,恰有一人获得一等奖就是甲获得乙没获得或甲没获得乙获得,则所求概率是
,故选D
11、答案:
解析:从红、绿、黄、紫、白、蓝 6 种不同的颜色中任选 2 种, 共有 15 种不同的情况, 其中没有
选红色的所有情况为 (绿, 黄), (绿, 紫), (绿,白), (绿, 蓝), (黄, 紫), (黄, 白), (黄, 蓝), (紫, 白), (紫, 蓝),
(白, 蓝), 共 10 种, 故 所求概率为 .
12、答案:
解析:由题意知本题是一个古典概型,
试验发生包含的事件是一颗骰子连续掷两次,共有 种结果,
满足条件的事件是使复数 为实数,
要使的这是一个实数,
有 ,
有 ,共有 3 种结
果,
∴ 由古典概型得到
13、答案:0.38
解析:设甲地降雨为事件 ,乙地降雨为事件 ,
则两地恰有一地降雨为 ,故本题的正确答案为0.38
14、答案:
解析:取两个不同的数 , 记为有序数对 , 所有基本事件为:
共 6 种, 满足 的情况为: , 一共 2 种,
所以其概率为 .
15、答案:
解析:由题意知:甲、乙两人共答对三个题的基本事件有{甲答对2个乙答对1个,甲答对1个乙
答对2个},而甲答对每个题的概率为 ,乙答对每个题的概率为 .
∴甲答对2个乙答对1个的概率为 ,甲答对1个乙答对2个的概率为
,∴甲、乙两人共答对三个题的概率为 .故答案为: .
16、答案:(1) .
(2)概率为 .
解析:(1)从袋中随机取两个球,其一切可能的结果组成的样本点有:1和2,1和3,1和4,2和
3,2和4,3和4,共6个.
从袋中取出的两个球的编号之和不大于4的事件有:1和2,1和3,共2个,
因此所求事件的概率为 .
(2)先从袋中随机取一个球,记下编号为,放回后,再从袋中随机取一个球,记下编号为m,试验的样本空间
,
共16个样本点.
又满足条件 的样本点有: ,共3个.
所以满足条件 的事件的概率为 ,故满足条件 的事件的概率为
.
17、答案:(1)摸出的2个小球的所有可能的结果为 , , , , , ,
, , , .
(2)获得一等奖的概率为 .获得二等奖的概率为 .
解析:(1)摸出的2个小球的所有可能的结果为 , , , , , ,
, , , .
(2)由(1)知,摸出的2个小球的所有可能的结果共有10个,
摸出的2个小球都是偶数的所有可能的结果为 ,
所以获得一等奖的概率为 .
摸出的2个小球都是奇数的所有可能的结果为 , , ,
所以获得二等奖的概率为 .
18、答案:(1)
(2)概率为
(3)概率为
解析:(1)设该厂这个月共生产轿车n辆,
由题意得 ,所以 .
则 .
(2)设所抽样本中有a辆舒适型轿车,由题意得 ,即 .
因此抽取的容量为5的样本中,有2辆舒适型轿车,3辆标准型轿车.
用 表示2辆舒适型轿车,用 表示3辆标准型轿车,用E表示事件“在该样本中任取2辆,其中至少有1辆舒适型轿车”,
则试验的样本空间为
,共10个样
本点.
事件E包含的样本点有: ,共7个.
故 ,即所求概率为 .
(3)样本平均数 .
设D表示事件“从样本中任取一个数,该数与样本平均数之差的绝对值不超过0.5”,
则基本事件空间中有8个基本事件,事件D包含的基本事件为:9.4,8.6,9.2,8.7,9.3,9.0,共
6个,所以 ,即所求概率为 .
19、答案:概率为
解析:设元件1,2,3的使用寿命超过1000小时的事件分别记为A,B,C,
显然 ,
所以该部件的使用寿命超过1000小时的事件为 ,
所以该部件的使用寿命超过1000小时的概率 .