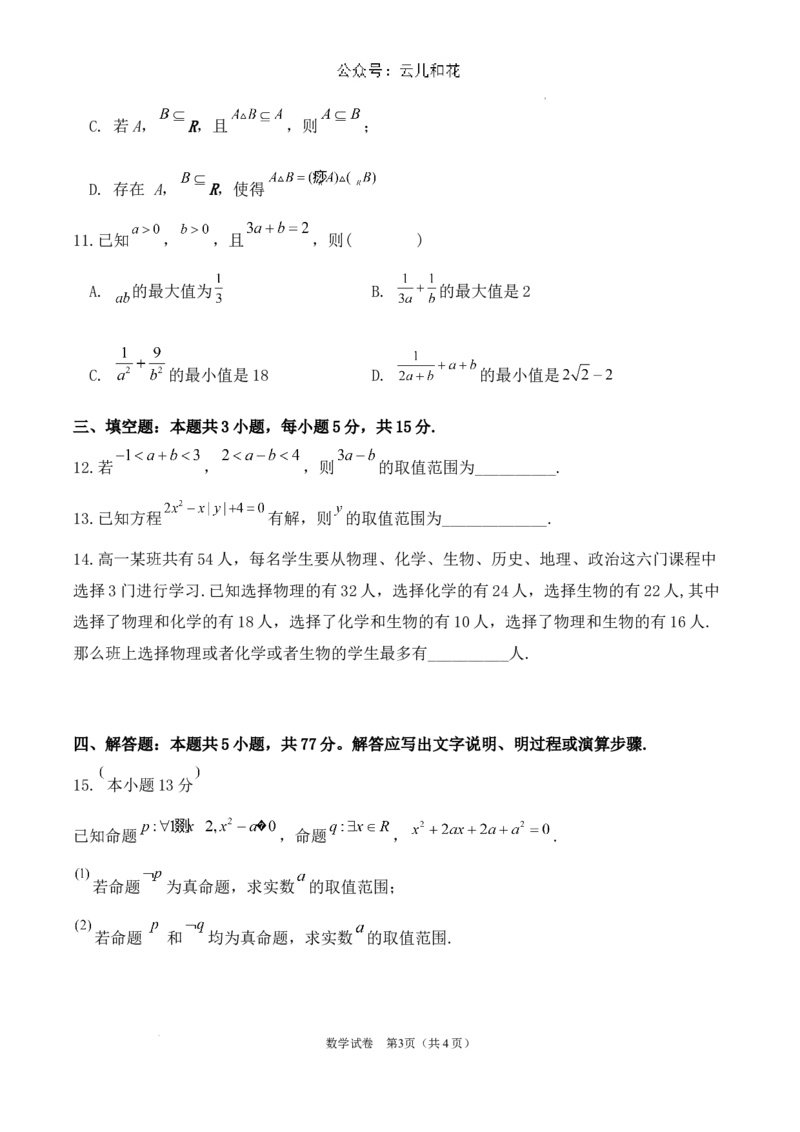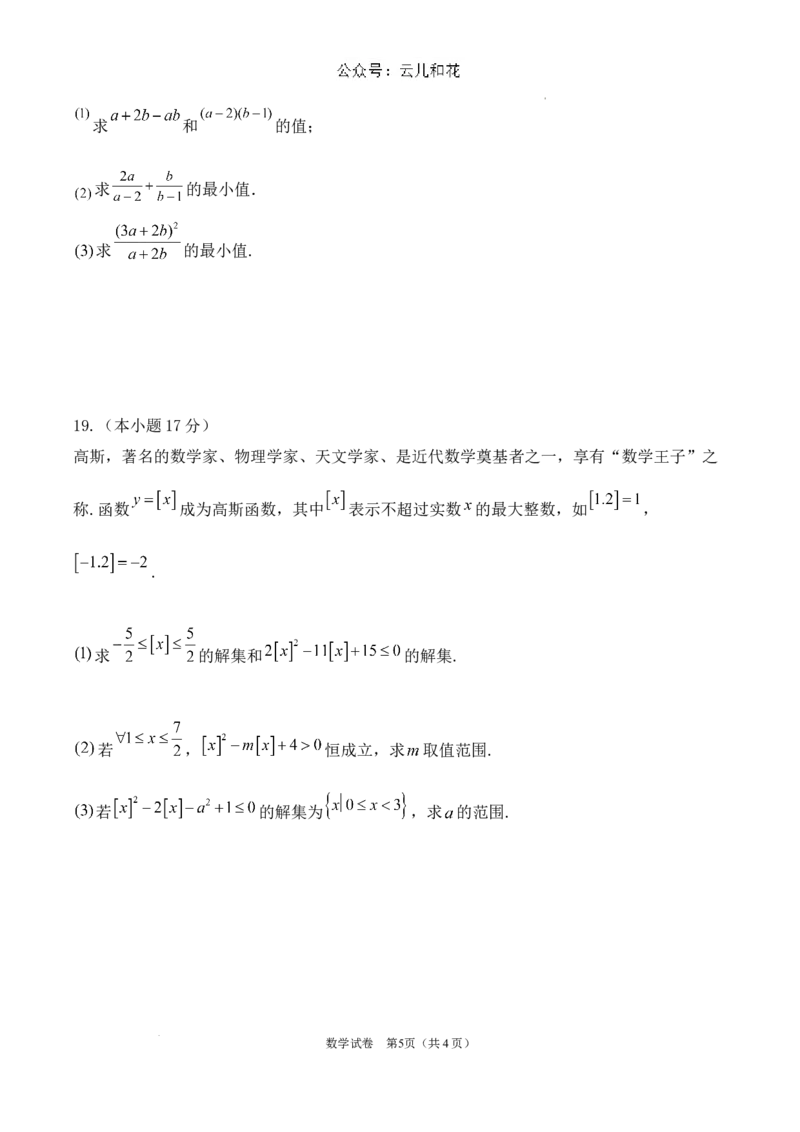2024级2024年9月月考数学卷_2024-2025高一（7-7月题库）_2024年10月试卷_1006湖北省荆州中学2024-2025学年高一上学期9月月考

荆州中学 2024～2025 学年高一九月月考 数学试题 命题人： 审题人： （全卷满分150分 考试用时120分钟） 一、单选题：本题共8小题，每小题5分，共40分.在每小题给出的选项中，只有一项是符 合题目要求的. 1.若 ，则 的值为( ) A. 或1或2 B. 或1 C. 或2 D. 2 2.设集合 ， ， ，则 ( ) A. B. C. D. 3.已知集合 ， ， ，则集合 的关系是( ) A. B. C. D. 4.设等腰三角形 的腰长为 ，底边长为 ，且 ，则“ 的周长为16”是“ 其中一条边长为6”的( ) A. 充分不必要条件 B. 必要不充分条件 C. 充要条件 D. 既不充分也不必要条件 5.下面命题正确的是( ) A. 已知 ，则“ ”是“ ”的充要条件 B. 命题“若 ，使得 ”的否定是“ ” 数学试卷 第1页（共4页） 学科网（北京）股份有限公司C. 已知 ，则“ ”是“ ”的既不充分也不必要条件 D. 已知 ，则“ ”是“ ”的必要不充分条件 6.已知 ，下列选项中正确的是( ) A. B. C. D. 7.已知正实数 ， 满足 ，则4x3y的最小值为( ) A. 24 B. 25 C. 26 D. 27 8.若不等式 有且只有三个整数解，实数 的取值范围为( ) A. B. C. D. 二、多选题：本题共3小题，每小题6分，共18分.在每小题给出的选项中，有多项符合题 目要求.全部选对得6分，部分选对的得部分分，选对但不全的得部分分，有选错的得0分. 9.设全集为U，在下列选项中，是 的充要条件的有( ) A. B. C. D. 10.对任意A， R，记 ，并称 为集合A，B的对称差．例如， 若 ， ，则 ，下列命题中，为真命题的是 ( ) A. 若A， R，且 ，则 ； B. 若A， R，且 ，则 ； 数学试卷 第2页（共4页） 学科网（北京）股份有限公司C. 若A， R，且 ，则 ； D. 存在 A， R，使得 11.已知 ， ，且 ，则( ) A. 的最大值为 B. 的最大值是2 C. 的最小值是18 D. 的最小值是 三、填空题：本题共3小题，每小题5分，共15分. 12.若 ， ，则 的取值范围为__________. 13.已知方程 有解，则 的取值范围为_____________. 14.高一某班共有54人，每名学生要从物理、化学、生物、历史、地理、政治这六门课程中 选择3门进行学习.已知选择物理的有32人，选择化学的有24人，选择生物的有22人,其中 选择了物理和化学的有18人，选择了化学和生物的有10人，选择了物理和生物的有16人. 那么班上选择物理或者化学或者生物的学生最多有__________人. 四、解答题：本题共5小题，共77分。解答应写出文字说明、明过程或演算步骤. 15. 本小题13分 已知命题 ，命题 ， . 若命题 为真命题，求实数 的取值范围； 若命题 和 均为真命题，求实数 的取值范围. 数学试卷 第3页（共4页） 学科网（北京）股份有限公司16.(本小题15分）   A x4xx2 0 已知集合 , ， ，. 当 时，求 . 若 ，求 范围. 17. 本小题15分 为了丰富学生的课余生活、给学生更好的校园生活体验．学校决定在原有的矩形花园ABCD 的基础上，拓展建成一个更大的矩形花园AMPN为了方便施工，建造时要求B点在AM 上，点 D AN MN C 在 上，且对角线 过点 ，如图所示．已知 DN AMPN 当 的长度为多少时，矩形 的面积最小？并求出最小面积． AMPN DN 要使矩形 的面积大于 ，则 的长应在什么范围内？ 18. 本小题17分 设 ， 为正实数，且 数学试卷 第4页（共4页） 学科网（北京）股份有限公司求 和 的值； 求 的最小值． 求 的最小值. 19.（本小题17分） 高斯，著名的数学家、物理学家、天文学家、是近代数学奠基者之一，享有“数学王子”之 称.函数 成为高斯函数，其中 表示不超过实数 的最大整数，如 ， . 求 的解集和 的解集. 若 ， 恒成立，求 取值范围. 若 的解集为 ，求 的范围. 数学试卷 第5页（共4页） 学科网（北京）股份有限公司