文档内容
高一数学试题参考答案
一、选择题:本题共8小题,每小题5分,共40分,在每小题给出的四个选项中,只有一项
是符合要求的.
1.A 2.A 3.C 4.D 5.B 6.B 7. B 8.B
二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题
目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.
9.ACD 10.BCD 11.ABD
三、填空题:本题共3小题,每小题5分,共15分.
π
12.-12 13.2 3 14.
6
四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.
15.(13分)
解:(1)根据正弦定理,因为b ( cosC +1 )= c ( 2- cosB ) ,
所以sinBcosC+sinB =2sinC- sinCcosB; ...........2分
整理得sinBcosC+sinCcosB+sinB =2sinC,
所以sin ( B+C )+sinB = 2sinC,
因为A+B+C =π,所以sinA=sin ( B+C )
,
所以sinA+sinB =2sinC ,...........5分
由正弦定理可得a+b=2c;...........6分
9
(2)因为cosC = ,由余弦定理可得c2 =a2 +b2 - 2abcosC,
16
9
即25=a2 +b2 - ab, ...........8分
8
25
又c=5,故a+b=10,从而25+ ab=(a+b)2 =100,解得ab=24,
8
...........10分
9 5 7
因为cosC = ,所以sinC = 1- cos2C= ,...........11分
16 16
1 1 5 7 15 7
所以S = absinC = · 24· = . ...........13分
△ABC
2 2 16 4
高一数学答案 第1页(共4页)
{#{QQABZYQQogAIAJAAAQgCAQ3aCEOQkBAACSgOhEAAMAAAgRNABAA=}#}16.(15分)
解:(1)根据分层抽样知:
应抽取小吃类80· ( 1- 30-% 1-5% -10%- 5%= 5% ) 28家,
生鲜类80· 15%= 12家,
所以应抽取小吃类28家,生鲜类12家. ...........4分
(2)(i)根据题意可得 ( 0.002· 3+ 2a+ 0.006·) 5=0 1,解得a=0.004,...........6分
设75百分位数为x,因为 ( 0.002+0.004+0.006 )· 50= 0.6,
所以 ( x- 450·) 0.00+4 0=.6 0.75,解得x=487.5,
所以该直播平台商家平均日利润的75百分位数为487.5元. ...........9分
平均数为
( 325· 0.002+ 375· 0.00+4 42· 5 0.0+06 4· 75 0+.004 · 525 +0.002· 575 0.002 )
· 50= 440,
所以该直播平台商家平均日利润的平均数为440元. ...........12分
500- 480
(ii) · 0.004+ 0.002+ 0.002· 5· 0 10=00 280,
50
所以估计该直播平台“优秀商家”的个数为280. ...........15分
17.(5分)
解:(1)从中任取一球,分别记得到红球、黄球、蓝球为事件A,B,C,
因为A,B,C为两两互斥事件, ...........1分
1
P(A)= ,
P(A)+P(B)+P(C)=1,
2
3 1
由已知得P(A)+P(B)= , 解得P(B)= ,...........5分
4 4
1 1
P(B)+P(C)= , P(C)= ,
2 4
所以盒中红球、黄球、蓝球的个数分别是2,1,1; ...........6分
(2)(i)由(1)知红球、黄球、蓝球个数分别为2,1,1,用 1,2表示红球,用a表示
黄球,用b表示蓝球,m表示第一次取出的球,n表示第二次取出的球,(m,n)表示
试验的样本点,
则样本空间W= {(1,1),(1,2),(1,a),(1,b),(2,1),(2,2),(2,a),(2,b),(a,1),(a,2),
(a,a),(a,b),(b,1),(b,2),(b,a),(b,b)};...........10分
高一数学答案 第2页(共4页)
{#{QQABZYQQogAIAJAAAQgCAQ3aCEOQkBAACSgOhEAAMAAAgRNABAA=}#}(ii)由(i)得n(W =) 16,记“取到两个球颜色相同”为事件M ,“取到两个球颜色
不相同”为事件N ,
6 3
则n(M)=6,所以P(M)= = ,...........12分
16 8
3 5
所以P(N)=1- P(M=) 1- = ,...........13分
8 8
5 3
因为 > ,所以此游戏不公平............15分
8 8
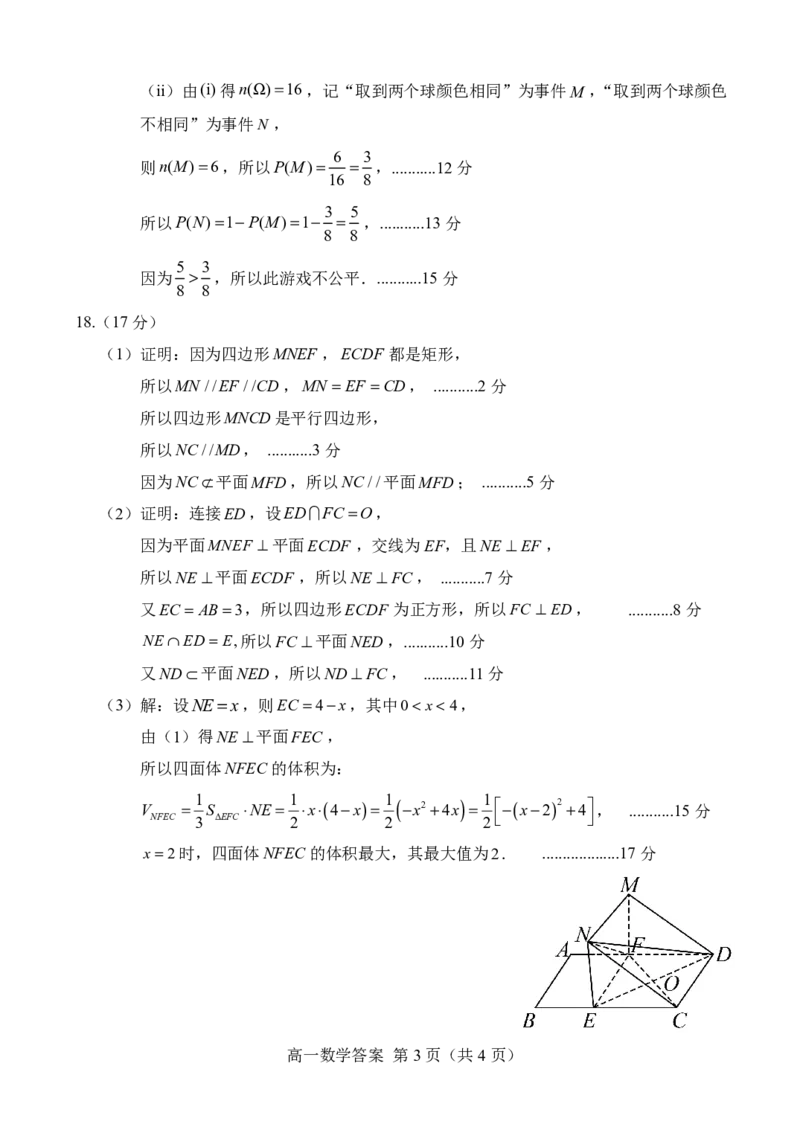
18.(17分)
(1)证明:因为四边形MNEF,ECDF 都是矩形,
所以MN //EF//CD,MN =EF =CD, ...........2分
所以四边形MNCD是平行四边形,
所以NC//MD, ...........3分
因为NC¸ 平面MFD,所以NC//平面MFD; ...........5分
(2)证明:连接ED,设ED∩FC=O,
因为平面MNEF ^ 平面ECDF ,交线为EF,且NE^ EF,
所以NE ^ 平面ECDF ,所以NE^ FC, ...........7分
又EC= AB=3,所以四边形ECDF 为正方形,所以FC ^ ED, ...........8分
NE˙ ED= E,所以FC ^ 平面NED,...........10分
又ND(cid:204) 平面NED,所以ND^ FC, ...........11分
(3)解:设NE=x,则EC =4- x,其中0< x<4,
由(1)得NE ^ 平面FEC,
所以四面体NFEC的体积为:
V = 1 S (cid:215) NE= 1 (cid:215) x(cid:215) (-4 =x ) - 1( +x2 =4x ) - 1 - (+x 2 )2 4 , ...........15分
NFEC 3 ΔEFC 2 2 2
x=2时,四面体NFEC的体积最大,其最大值为2. ...................17分
高一数学答案 第3页(共4页)
{#{QQABZYQQogAIAJAAAQgCAQ3aCEOQkBAACSgOhEAAMAAAgRNABAA=}#}19.(17分)
解:(1)因为cos2B+cos2C- cos2A= 1,即1- 2sin2B+ 1- 2sin2-C+ 1 2sin=2 A 1,
故sin2 A=sin2B+sin2C,由正弦定理可得a2 =b2 +c2,..........3分
π
故D ABC直角三角形,即A= ;..........4分
2
p
(2)由(1)可得A= ,所以三角形ABC的三个角都小于120(cid:176) ,
2
则由费马点定义可知:— APB=— BP=C— =APC(cid:176) 120 ,..........5分
(cid:3)(cid:3)(cid:3)(cid:4) (cid:3)(cid:3)(cid:3)(cid:4) (cid:3)(cid:3)(cid:3)(cid:4)
设|PA|=x,|PB|= y,|PC|=z,
1 3 1 3 1 3 1
由S +S +S =S ,得 xy(cid:215) + yz(cid:215) + xz(cid:215) = · 2,
D APB D BPC D APC D ABC
2 2 2 2 2 2 2
4 3
整理得xy+ yz+xz= ,..................8分
3
(cid:3)(cid:3)(cid:3)(cid:4) (cid:3)(cid:3)(cid:3)(cid:4) (cid:3)(cid:3)(cid:3)(cid:4) (cid:3)(cid:3)(cid:3)(cid:4) (cid:3)(cid:3)(cid:3)(cid:4) (cid:3)(cid:3)(cid:3)(cid:4)
1 1 1 1 4 3 2 3
则PA(cid:215) PB+ PB(cid:215) PC+ PA(cid:215) PC= x(cid:215)y- ( + ) (cid:215) -yz +( (cid:215))- xz=-( · ) =- ;
2 2 2 2 3 3
..................10分
2π
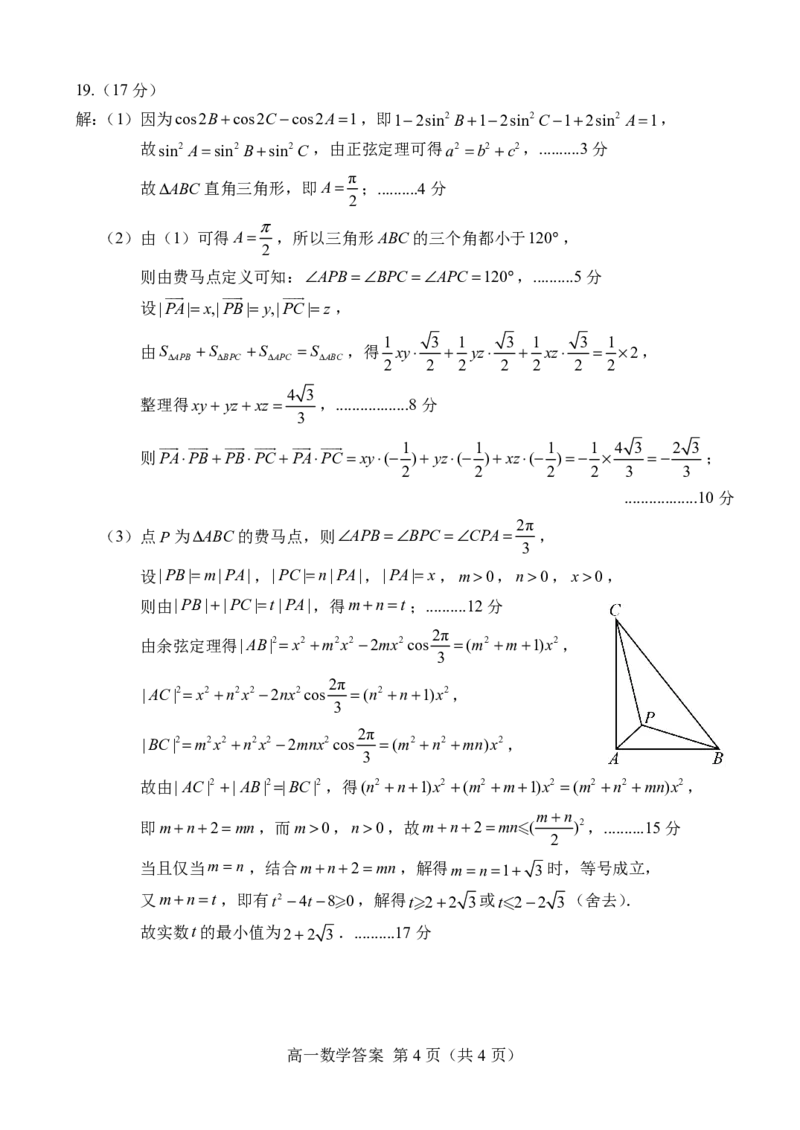
(3)点P为D ABC的费马点,则— APB=— BP=C— =CPA ,
3
设|PB|=m|PA|,|PC|=n|PA|,|PA|=x,m>0,n>0,x>0,
则由|PB|+|PC|=t|PA|,得m+n=t;..........12分
2π
由余弦定理得|AB|2=x2+m2x2- 2mx2cos = (m2+ m+ 1)x2,
3
2π
|AC|2=x2 +n2x2- 2nx2cos = (n2+ n+ 1)x2,
3
2π
|BC|2=m2x2+n2x2 - 2mnx2cos = (m2+ n2+ mn)x2,
3
故由|AC|2 +|AB|2=|BC|2,得(n2 +n+1)x2 +(m2 +m+1)x2 =(m2 +n2 +mn)x2,
m+n
即m+n+2=mn,而m>0,n>0,故m+n+2=mn(cid:1)( )2,..........15分
2
当且仅当m=n,结合m+n+2=mn,解得m=n=1+ 3时,等号成立,
又m+n=t,即有t2 - 4-t 8(cid:2)0,解得t(cid:2)2+2 3或t(cid:1)2- 2 3(舍去).
故实数t的最小值为2+2 3...........17分
高一数学答案 第4页(共4页)
{#{QQABZYQQogAIAJAAAQgCAQ3aCEOQkBAACSgOhEAAMAAAgRNABAA=}#}