文档内容
期中检测卷 02
姓名:__________________ 班级:______________ 得分:_________________
注意事项:
本试卷满分150分,考试时间120分钟,试题共22题.答卷前,考生务必用0.5毫米黑色签字笔将自
己的姓名、班级等信息填写在试卷规定的位置.
一、选择题(本大题共8小题,每小题5分,共40分)在每小题所给出的四个选项中,只有一项是符合题
目要求的.
1.点C是线段AB靠近点B的三等分点,下列正确的是( )
A. B. C. D.
【答案】D
【分析】根据共线向量的定义即可得结论.
【解答】解:由题,点C是线段AB靠近点B的三等分点,
=3 =﹣3 ,所以选项A错误;
=2 =﹣2 ,所以选项B和选项C错误,选项D正确.
故选:D.
【知识点】平行向量(共线)、向量数乘和线性运算
2.已知复数z满足z(3+i)=3+i2020,其中i为虚数单位,则z的共轭复数 的虚部为( )
A. B. C. D.
【答案】D
【分析】直接利用复数代数形式的乘除运算化简,然后利用共轭复数的概念得答案.
【解答】解:∵z(3+i)=3+i2020,i2020=(i2)1010=(﹣1)1010=1,
∴z(3+i)=4,∴z= ,
∴ = ,
∴共轭复数 的虚部为 ,
故选:D.
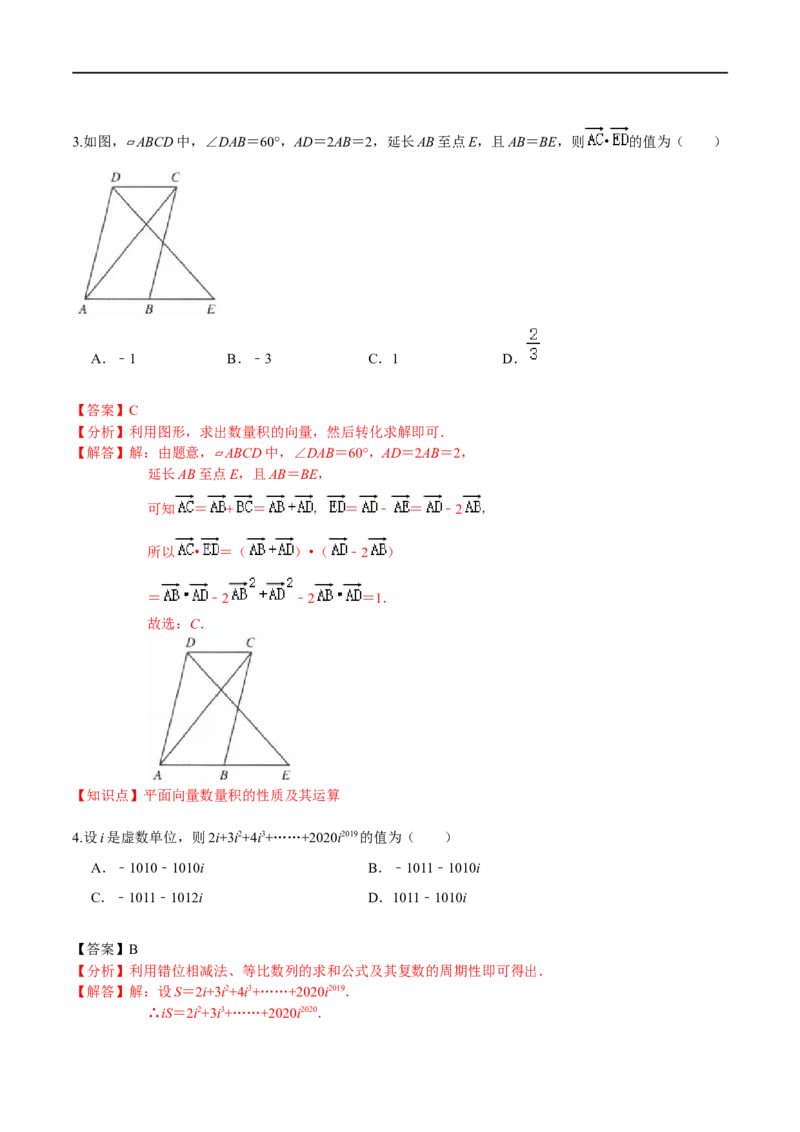
【知识点】复数的运算3.如图, ▱ABCD中,∠DAB=60°,AD=2AB=2,延长AB至点E,且AB=BE,则 • 的值为( )
A.﹣1 B.﹣3 C.1 D.
【答案】C
【分析】利用图形,求出数量积的向量,然后转化求解即可.
【解答】解:由题意, ▱ABCD中,∠DAB=60°,AD=2AB=2,
延长AB至点E,且AB=BE,
可知 = + = , = ﹣ = ﹣2 ,
所以 • =( )•( ﹣2 )
= ﹣2 ﹣2 =1.
故选:C.
【知识点】平面向量数量积的性质及其运算
4.设i是虚数单位,则2i+3i2+4i3+……+2020i2019的值为( )
A.﹣1010﹣1010i B.﹣1011﹣1010i
C.﹣1011﹣1012i D.1011﹣1010i
【答案】B
【分析】利用错位相减法、等比数列的求和公式及其复数的周期性即可得出.
【解答】解:设S=2i+3i2+4i3+……+2020i2019.
∴iS=2i2+3i3+……+2020i2020.则(1﹣i)S=i+i+i2+i3+……+i2019﹣2020i2020.
= =i+
= =﹣2021+i,
∴S= = .
故选:B.
【知识点】复数的运算
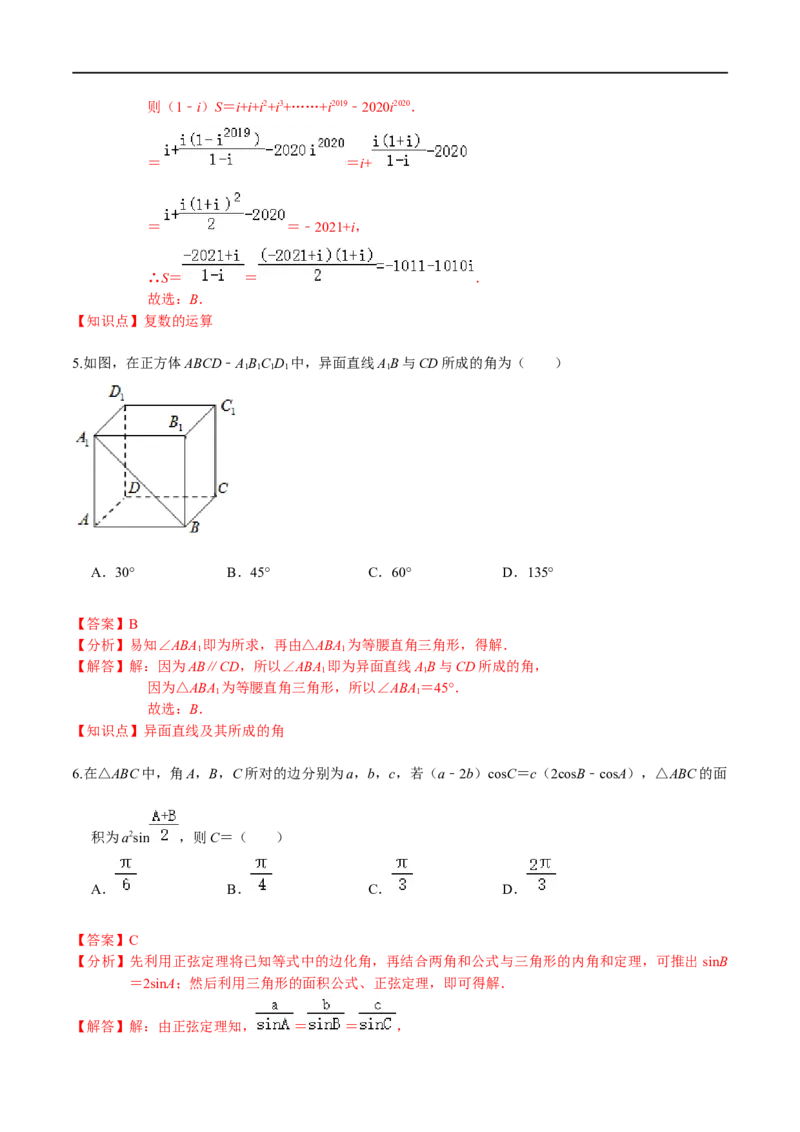
5.如图,在正方体ABCD﹣ABC D 中,异面直线AB与CD所成的角为( )
1 1 1 1 1
A.30° B.45° C.60° D.135°
【答案】B
【分析】易知∠ABA 即为所求,再由△ABA 为等腰直角三角形,得解.
1 1
【解答】解:因为AB∥CD,所以∠ABA 即为异面直线AB与CD所成的角,
1 1
因为△ABA 为等腰直角三角形,所以∠ABA=45°.
1 1
故选:B.
【知识点】异面直线及其所成的角
6.在△ABC中,角A,B,C所对的边分别为a,b,c,若(a﹣2b)cosC=c(2cosB﹣cosA),△ABC的面
积为a2sin ,则C=( )
A. B. C. D.
【答案】C
【分析】先利用正弦定理将已知等式中的边化角,再结合两角和公式与三角形的内角和定理,可推出sinB
=2sinA;然后利用三角形的面积公式、正弦定理,即可得解.
【解答】解:由正弦定理知, = = ,∵(a﹣2b)cosC=c(2cosB﹣cosA),
∴(sinA﹣2sinB)cosC=sinC(2cosB﹣cosA),
即sinAcosC+sinCcosA=2(sinBcosC+cosBsinC),
∴sin(A+C)=2sin(B+C),即sinB=2sinA.
∵△ABC的面积为a2sin ,
∴S= bcsinA=a2sin ,
根据正弦定理得, sinB•sinC•sinA=sin2A•sin ,
化简得,sinB•sin cos =sinA•cos ,
∵ ∈(0, ),∴cos >0,
∴sin = = ,
∴ = ,即C= .
故选:C.
【知识点】正弦定理、余弦定理
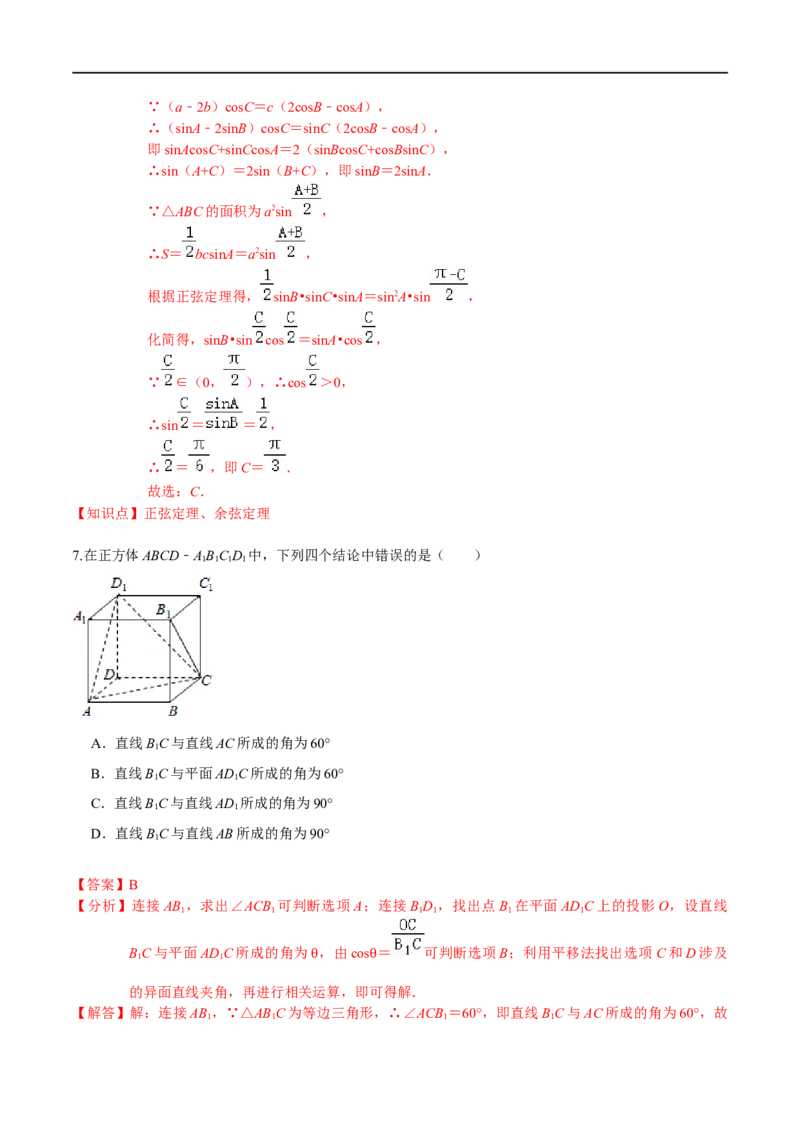
7.在正方体ABCD﹣ABC D 中,下列四个结论中错误的是( )
1 1 1 1
A.直线BC与直线AC所成的角为60°
1
B.直线BC与平面ADC所成的角为60°
1 1
C.直线BC与直线AD 所成的角为90°
1 1
D.直线BC与直线AB所成的角为90°
1
【答案】B
【分析】连接AB ,求出∠ACB 可判断选项A;连接BD ,找出点B 在平面ADC上的投影O,设直线
1 1 1 1 1 1
BC与平面ADC所成的角为 ,由cos = 可判断选项B;利用平移法找出选项C和D涉及
1 1
θ θ
的异面直线夹角,再进行相关运算,即可得解.
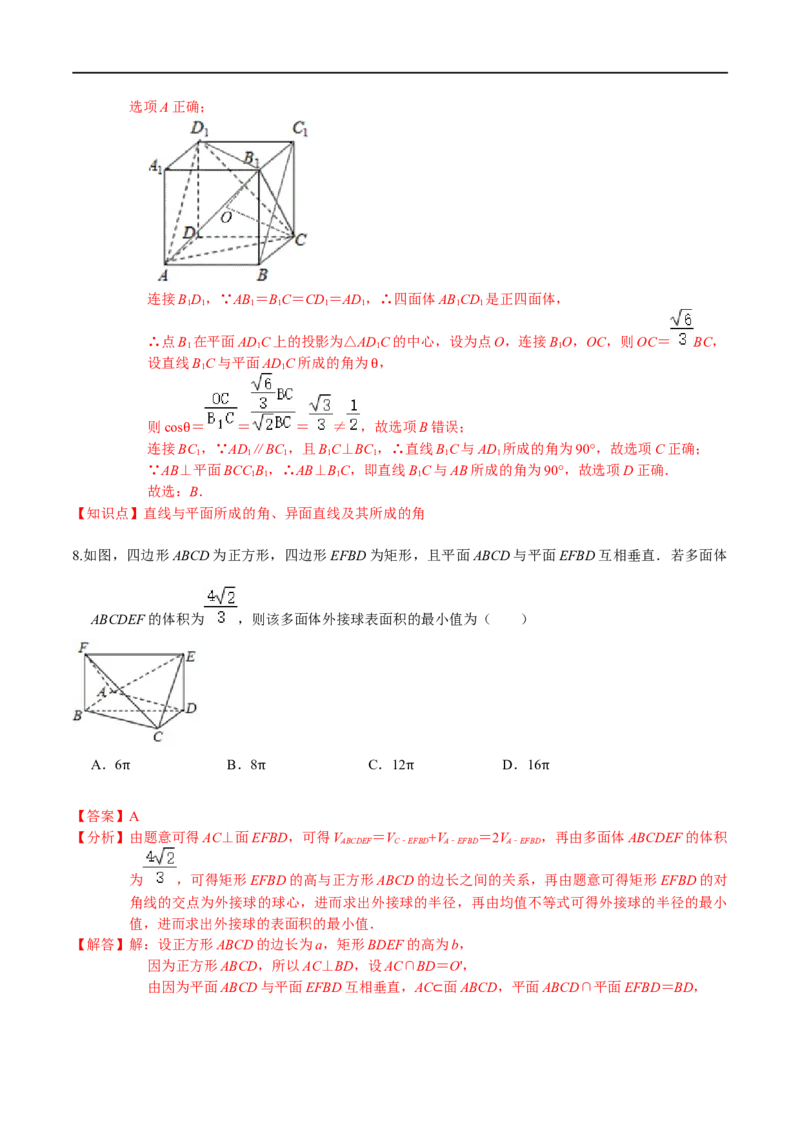
【解答】解:连接AB ,∵△ABC为等边三角形,∴∠ACB =60°,即直线BC与AC所成的角为60°,故
1 1 1 1选项A正确;
连接BD,∵AB=BC=CD=AD,∴四面体ABCD 是正四面体,
1 1 1 1 1 1 1 1
∴点B 在平面ADC上的投影为△ADC的中心,设为点O,连接BO,OC,则OC= BC,
1 1 1 1
设直线BC与平面ADC所成的角为 ,
1 1
θ
则cos = = = ≠ ,故选项B错误;
连接BC ,∵AD∥BC ,且BC⊥BC ,∴直线BC与AD 所成的角为90°,故选项C正确;
θ 1 1 1 1 1 1 1
∵AB⊥平面BCC B,∴AB⊥BC,即直线BC与AB所成的角为90°,故选项D正确.
1 1 1 1
故选:B.
【知识点】直线与平面所成的角、异面直线及其所成的角
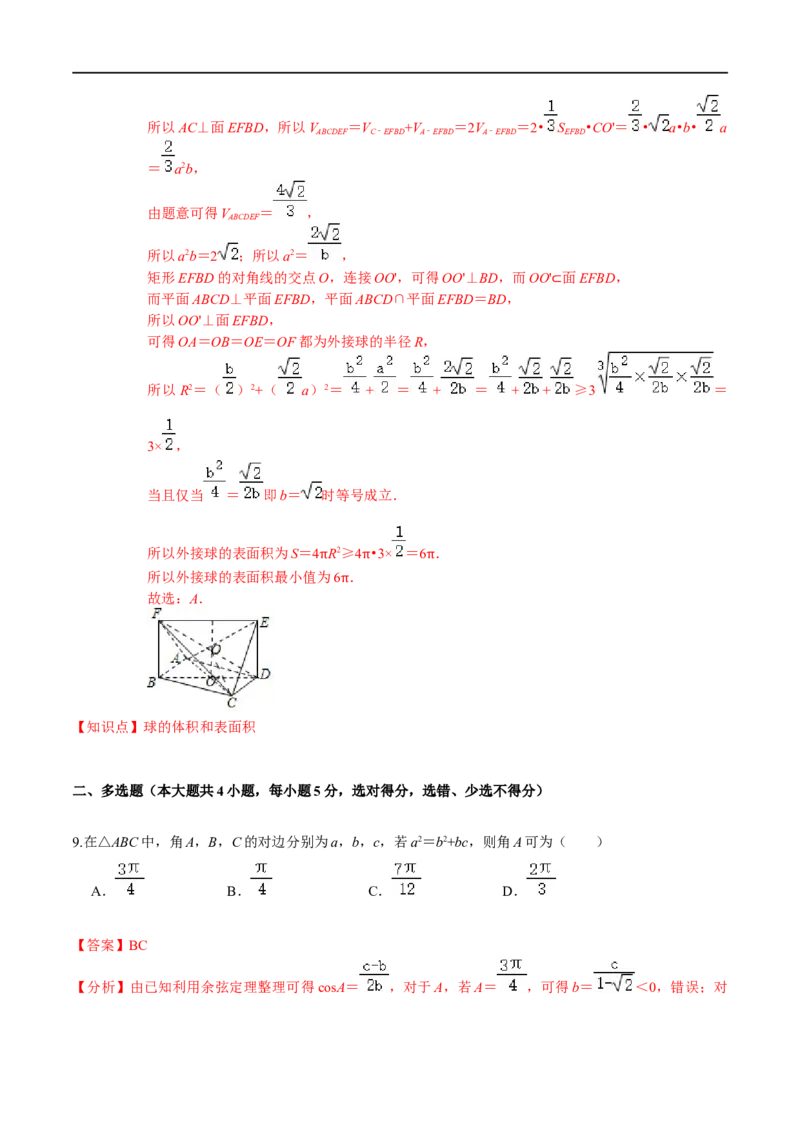
8.如图,四边形ABCD为正方形,四边形EFBD为矩形,且平面ABCD与平面EFBD互相垂直.若多面体
ABCDEF的体积为 ,则该多面体外接球表面积的最小值为( )
A.6 B.8 C.12 D.16
π π π π
【答案】A
【分析】由题意可得AC⊥面EFBD,可得V =V +V =2V ,再由多面体ABCDEF的体积
ABCDEF C﹣EFBD A﹣EFBD A﹣EFBD
为 ,可得矩形EFBD的高与正方形ABCD的边长之间的关系,再由题意可得矩形EFBD的对
角线的交点为外接球的球心,进而求出外接球的半径,再由均值不等式可得外接球的半径的最小
值,进而求出外接球的表面积的最小值.
【解答】解:设正方形ABCD的边长为a,矩形BDEF的高为b,
因为正方形ABCD,所以AC⊥BD,设AC∩BD=O',
由因为平面ABCD与平面EFBD互相垂直,AC 面ABCD,平面ABCD∩平面EFBD=BD,
⊂所以AC⊥面EFBD,所以V =V +V =2V =2• S •CO'= • a•b• a
ABCDEF C﹣EFBD A﹣EFBD A﹣EFBD EFBD
= a2b,
由题意可得V = ,
ABCDEF
所以a2b=2 ;所以a2= ,
矩形EFBD的对角线的交点O,连接OO',可得OO'⊥BD,而OO' 面EFBD,
而平面ABCD⊥平面EFBD,平面ABCD∩平面EFBD=BD,
⊂
所以OO'⊥面EFBD,
可得OA=OB=OE=OF都为外接球的半径R,
所以R2=( )2+( a)2= + = + = + + ≥3 =
3× ,
当且仅当 = 即b= 时等号成立.
所以外接球的表面积为S=4 R2≥4 •3× =6 .
所以外接球的表面积最小值为6 .
π π π
故选:A.
π
【知识点】球的体积和表面积
二、多选题(本大题共4小题,每小题5分,选对得分,选错、少选不得分)
9.在△ABC中,角A,B,C的对边分别为a,b,c,若a2=b2+bc,则角A可为( )
A. B. C. D.
【答案】BC
【分析】由已知利用余弦定理整理可得cosA= ,对于A,若A= ,可得b= <0,错误;对于B,若A= ,可得b= >0,对于C,若A= ,可得b= >0,对于D,
若A= ,可得c=0,错误,即可得解.
【解答】解:因为在△ABC中,a2=b2+bc,
又由余弦定理可得:a2=b2+c2﹣2bccosA,
所以b2+bc=b2+c2﹣2bccosA,
整理可得:c=b(1+2cosA),
可得:cosA= ,
对于A,若A= ,可得:﹣ = ,整理可得:b= <0,错误;
对于B,若A= ,可得: = ,整理可得:b= >0,
对于C,若A= ,可得:cos = = ,整理可得:b= >0,
对于D,若A= ,可得:cos =﹣ = ,整理可得:c=0,错误.
故选:BC.
【知识点】余弦定理
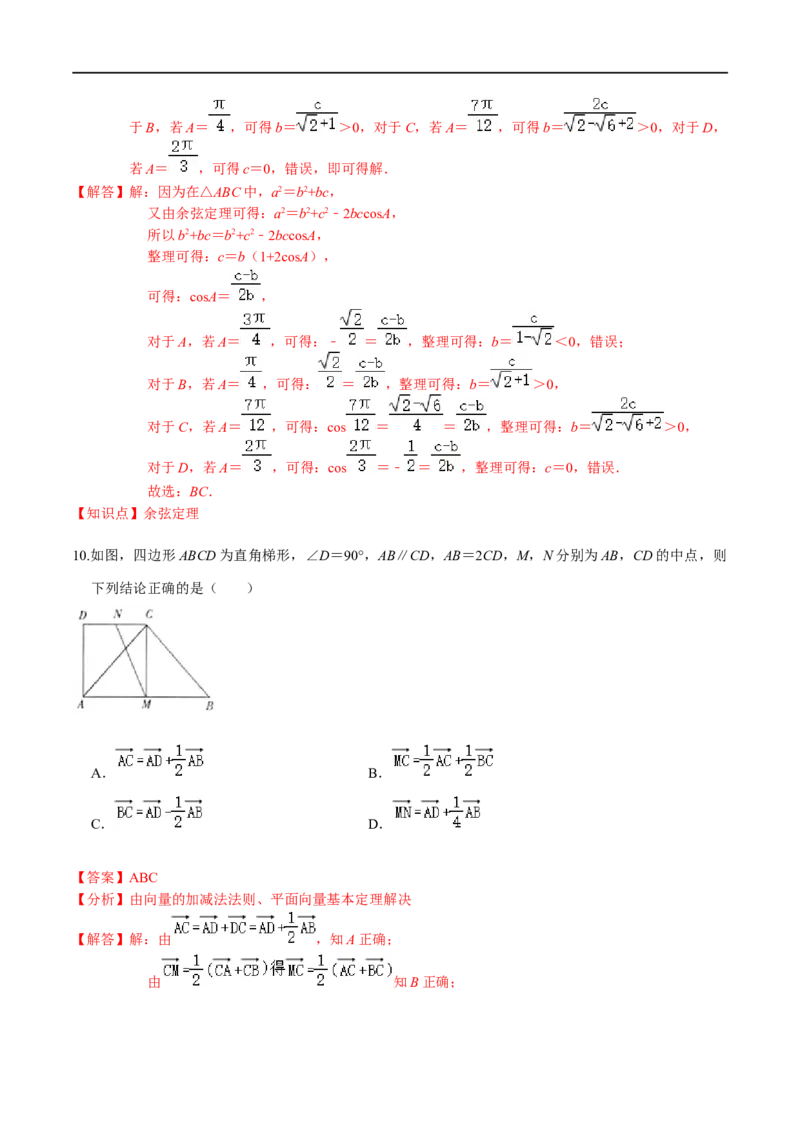
10.如图,四边形ABCD为直角梯形,∠D=90°,AB∥CD,AB=2CD,M,N分别为AB,CD的中点,则
下列结论正确的是( )
A. B.
C. D.
【答案】ABC
【分析】由向量的加减法法则、平面向量基本定理解决
【解答】解:由 ,知A正确;
由 知B正确;由 知C正确;
由N为线段DC的中点知 知D错误;
故选:ABC.
【知识点】向量数乘和线性运算、平面向量的基本定理
11.下列说法正确的有( )
A.任意两个复数都不能比大小
B.若z=a+bi(a R,b R),则当且仅当a=b=0时,z=0
C.若z,z C,且∈ z2+z∈2=0,则z=z=0
1 2 1 2 1 2
D.若复数z∈满足|z|=1,则|z+2i|的最大值为3
【答案】BD
【分析】通过复数的基本性质,结合反例,以及复数的模,判断命题的真假即可.
【解答】解:当两个复数都是实数时,可以比较大小,所以A不正确;
复数的实部与虚部都是0时,复数是0,所以B正确;
反例z=1,z=i,满足z2+z2=0,所以C不正确;
1 2 1 2
复数z满足|z|=1,则|z+2i|的几何意义,是复数的对应点到(0,﹣2)的距离,它的最大值为
3,所以D正确;
故选:BD.
【知识点】复数的模、复数的运算、虚数单位i、复数、命题的真假判断与应用
12.如图,已知ABCD﹣ABC D 为正方体,E,F分别是BC,AC的中点,则( )
1 1 1 1 1
A.
B.
C.向量 与向量 的夹角是60°
D.异面直线EF与DD 所成的角为45°
1【答案】ABD
【分析】在正方体ABCD﹣ABC D 中,建立合适的空间直角坐标系,设正方体的棱长为2,根据空间向量
1 1 1 1
的坐标运算,以及异面直线所成角的向量求法,逐项判断即可.
【解答】解:在正方体ABCD﹣ABC D 中,以点A为坐标原点,分别以AB,AD,AA 为x轴、y轴、z轴
1 1 1 1 1
建立空间直角坐标系,
设正方体的棱长为2,则A(0,0,0),A (0,0,2),B(2,0,0),B (2,0,2),C
1 1
(2,2,0),D(0,2,0),D(0,2,2),
1
所以 ,
故 ,故选项A正确;
又 ,
又 ,
所以 , ,
则 ,故选项B正确;
,
所以 ,
因此 与 的夹角为120°,故选项C错误;
因为E,F分别是BC,AC的中点,
1
所以E(2,1,0),F(1,1,1),
则 ,
所以 ,
又异面直线的夹角大于0°小于等于90°,
所以异面直线EF与DD 所成的角为45°,故选项D正确;
1
故选:ABD.【知识点】异面直线及其所成的角
三、填空题(本大题共4小题,每小题5分,共20分.不需写出解答过程,请把答案直接填写在横线上)
13.已知正方形ABCD的边长为2,点P满足 = ( + ),则| |= ; • = .
【分析】根据向量的几何意义可得P为BC的中点,再根据向量的数量积的运算和正方形的性质即可求出.
【解答】解:由 = ( + ),可得P为BC的中点,
则|CP|=1,
∴|PD|= = ,
∴ • = •( + )=﹣ •( + )=﹣ 2﹣ • =﹣1,
故答案为: ,﹣1.
【知识点】平面向量数量积的性质及其运算
14.若虛数z、z 是实系数一元二次方程x2+px+q=0的两个根,且 ,则pq= .
1 2
【答案】1
【分析】设z =a+bi,则z =a﹣bi,(a,b R),根据两个复数相等的充要条件求出z ,z ,再由根与系
1 2 1 2
数的关系求得p,q的值.
∈
【解答】解:由题意可知z 与z 为共轭复数,设z=a+bi,则z=a﹣bi,(a,b R且b≠0),
1 2 1 2
又 ,则a2﹣b2+2abi=a﹣bi, ∈
∴(2a+b)+(a+2b)i=1﹣i,∴ ,解得 .
∴z= + i,z= i,(或z= + i,z= i).
1 2 2 1
由根与系数的关系,得p=﹣(z+z)=1,q=z•z=1,
1 2 1 2
∴pq=1.
故答案为:1.
【知识点】复数的运算
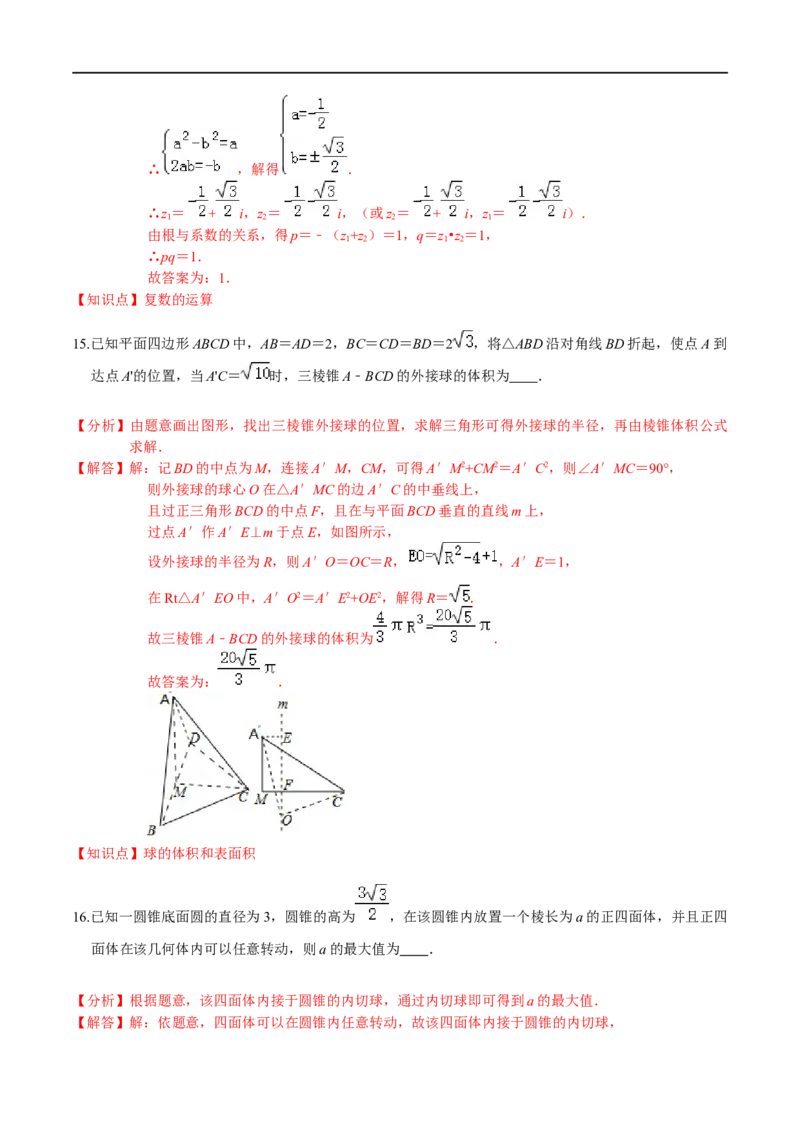
15.已知平面四边形ABCD中,AB=AD=2,BC=CD=BD=2 ,将△ABD沿对角线BD折起,使点A到
达点A'的位置,当A'C= 时,三棱锥A﹣BCD的外接球的体积为 .
【分析】由题意画出图形,找出三棱锥外接球的位置,求解三角形可得外接球的半径,再由棱锥体积公式
求解.
【解答】解:记BD的中点为M,连接A′M,CM,可得A′M2+CM2=A′C2,则∠A′MC=90°,
则外接球的球心O在△A′MC的边A′C的中垂线上,
且过正三角形BCD的中点F,且在与平面BCD垂直的直线m上,
过点A′作A′E⊥m于点E,如图所示,
设外接球的半径为R,则A′O=OC=R, ,A′E=1,
在Rt△A′EO中,A′O2=A′E2+OE2,解得R= .
故三棱锥A﹣BCD的外接球的体积为 .
故答案为: .
【知识点】球的体积和表面积
16.已知一圆锥底面圆的直径为3,圆锥的高为 ,在该圆锥内放置一个棱长为a的正四面体,并且正四
面体在该几何体内可以任意转动,则a的最大值为 .
【分析】根据题意,该四面体内接于圆锥的内切球,通过内切球即可得到a的最大值.
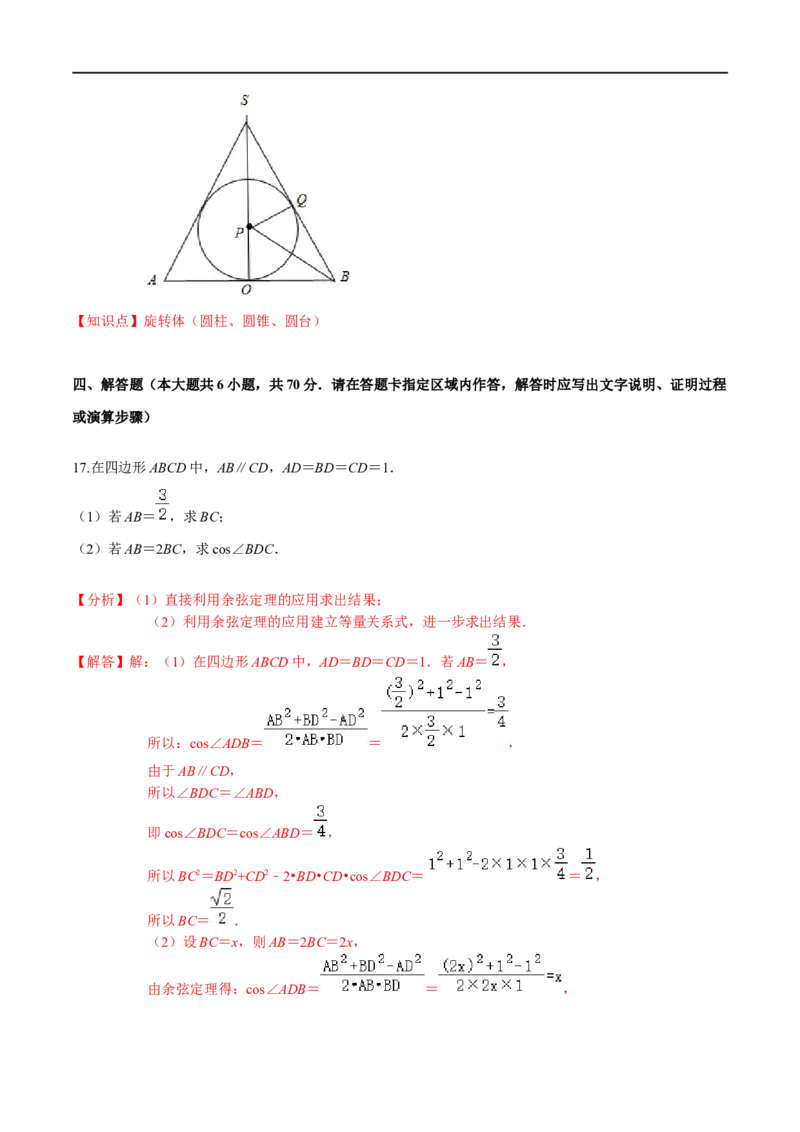
【解答】解:依题意,四面体可以在圆锥内任意转动,故该四面体内接于圆锥的内切球,设球心为P,球的半径为r,下底面半径为R,轴截面上球与圆锥母线的切点为Q,圆锥的轴截
面如图:
则OA=OB= ,
因为SO= ,
故可得:SA=SB= =3,
所以:三角形SAB为等边三角形,
故P是△SAB的中心,
连接BP,则BP平分∠SBA,
所以∠PBO=30°;
所以tan30°= ,即r= R= × = ,
即四面体的外接球的半径为r= .
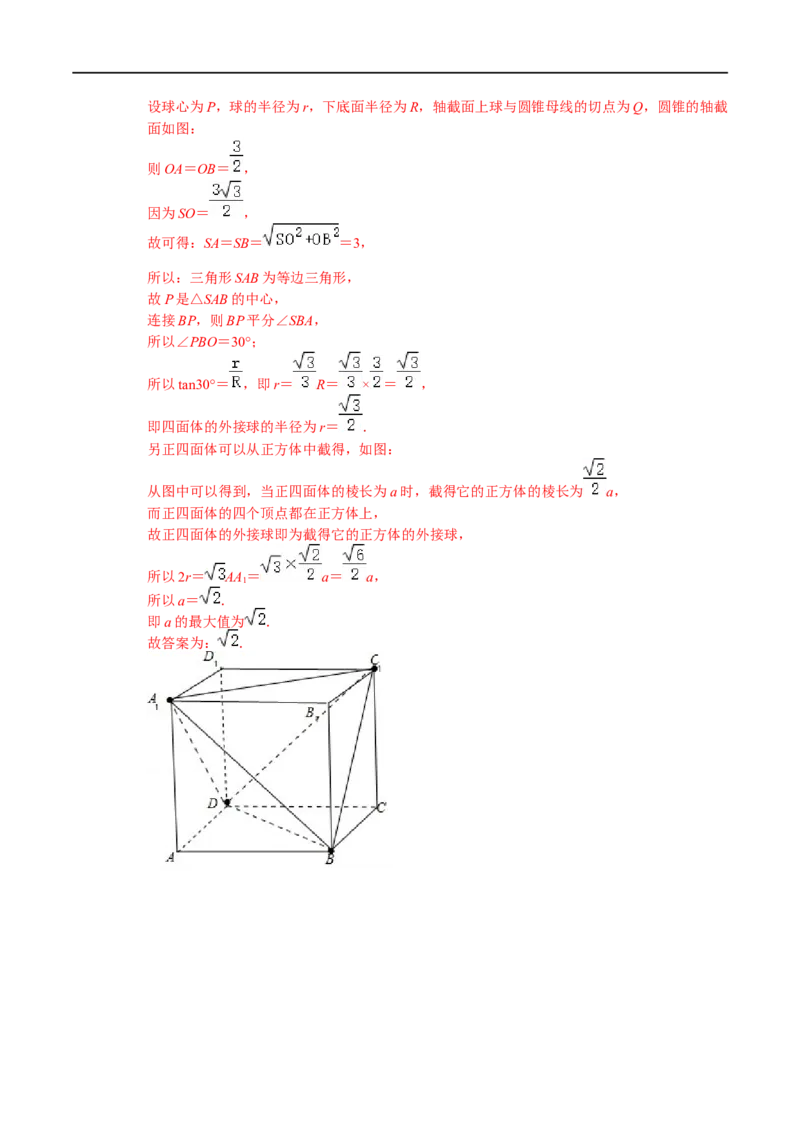
另正四面体可以从正方体中截得,如图:
从图中可以得到,当正四面体的棱长为a时,截得它的正方体的棱长为 a,
而正四面体的四个顶点都在正方体上,
故正四面体的外接球即为截得它的正方体的外接球,
所以2r= AA= a= a,
1
所以a= .
即a的最大值为 .
故答案为: .【知识点】旋转体(圆柱、圆锥、圆台)
四、解答题(本大题共6小题,共70分.请在答题卡指定区域内作答,解答时应写出文字说明、证明过程
或演算步骤)
17.在四边形ABCD中,AB∥CD,AD=BD=CD=1.
(1)若AB= ,求BC;
(2)若AB=2BC,求cos∠BDC.
【分析】(1)直接利用余弦定理的应用求出结果;
(2)利用余弦定理的应用建立等量关系式,进一步求出结果.
【解答】解:(1)在四边形ABCD中,AD=BD=CD=1.若AB= ,
所以:cos∠ADB= = ,
由于AB∥CD,
所以∠BDC=∠ABD,
即cos∠BDC=cos∠ABD= ,
所以BC2=BD2+CD2﹣2•BD•CD•cos∠BDC= = ,
所以BC= .
(2)设BC=x,则AB=2BC=2x,
由余弦定理得:cos∠ADB= = ,cos∠BDC= = = ,
故 ,
解得 或﹣ (负值舍去).
所以 .
【知识点】余弦定理
18.(1)已知z=1﹣2i,z=3+4i,求满足 = + 的复数z.
1 2
(2)已知z,ω为复数,(1+3i)﹣z为纯虚数,ω= ,且|ω|=5 .求复数ω.
【分析】(1)把z,z 代入 = + ,利用复数代数形式的乘除运算化简求出 ,进一步求出z;
1 2
(2)设z=a+bi(a,b∈R),利用复数的运算及(1+3i)•z=(1+3i)(a+bi)=a﹣3b+(3a+b)i
为 纯 虚 数 , 可 得 , 又 ω= = i , |ω|=5 , 可 得
,即可得出a,b,再代入可得ω.
【解答】解:(1)由z=1﹣2i,z=3+4i,
1 2
得 = + =
= ,
则z= ;
(2)设z=a+bi(a,b∈R),
∵(1+3i)•z=(1+3i)(a+bi)=a﹣3b+(3a+b)i为纯虚数,
∴ .
又ω= = = i,|ω|=5 ,
∴ .
把a=3b代入化为b2=25,解得b=±5,∴a=±15.
∴ω=±( i)=±(7﹣i).【知识点】复数的运算
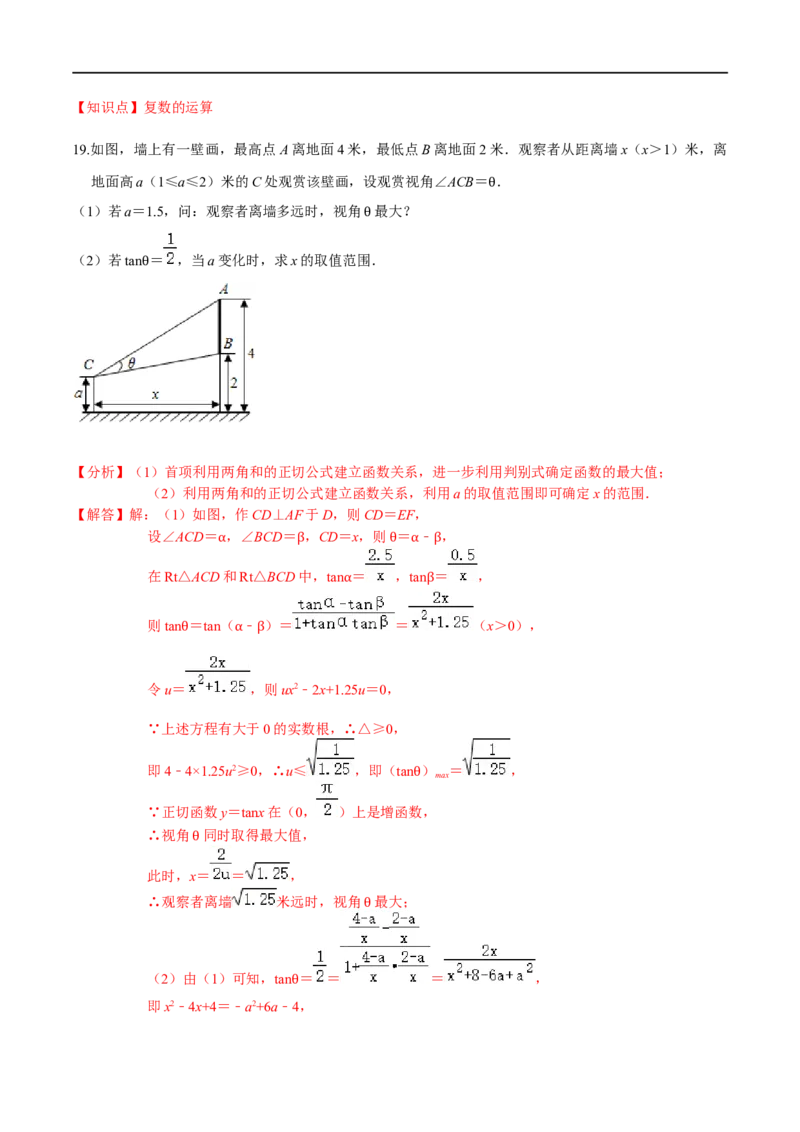
19.如图,墙上有一壁画,最高点A离地面4米,最低点B离地面2米.观察者从距离墙x(x>1)米,离
地面高a(1≤a≤2)米的C处观赏该壁画,设观赏视角∠ACB= .
(1)若a=1.5,问:观察者离墙多远时,视角 最大? θ
θ
(2)若tan = ,当a变化时,求x的取值范围.
θ
【分析】(1)首项利用两角和的正切公式建立函数关系,进一步利用判别式确定函数的最大值;
(2)利用两角和的正切公式建立函数关系,利用a的取值范围即可确定x的范围.
【解答】解:(1)如图,作CD⊥AF于D,则CD=EF,
设∠ACD= ,∠BCD= ,CD=x,则 = ﹣ ,
α β θ α β
在Rt△ACD和Rt△BCD中,tan = ,tan = ,
α β
则tan =tan( ﹣ )= = (x>0),
θ α β
令u= ,则ux2﹣2x+1.25u=0,
∵上述方程有大于0的实数根,∴△≥0,
即4﹣4×1.25u2≥0,∴u≤ ,即(tan ) = ,
max
θ
∵正切函数y=tanx在(0, )上是增函数,
∴视角 同时取得最大值,
θ
此时,x= = ,
∴观察者离墙 米远时,视角 最大;
θ
(2)由(1)可知,tan = = = ,
即x2﹣4x+4=﹣a2+6a﹣ θ4,∴(x﹣2)2=﹣(a﹣3)2+5,
∵1≤a≤2,
∴1≤(x﹣2)2≤4,
化简得:0≤x≤1或3≤x≤4,
又∵x>1,
∴3≤x≤4.
【知识点】解三角形
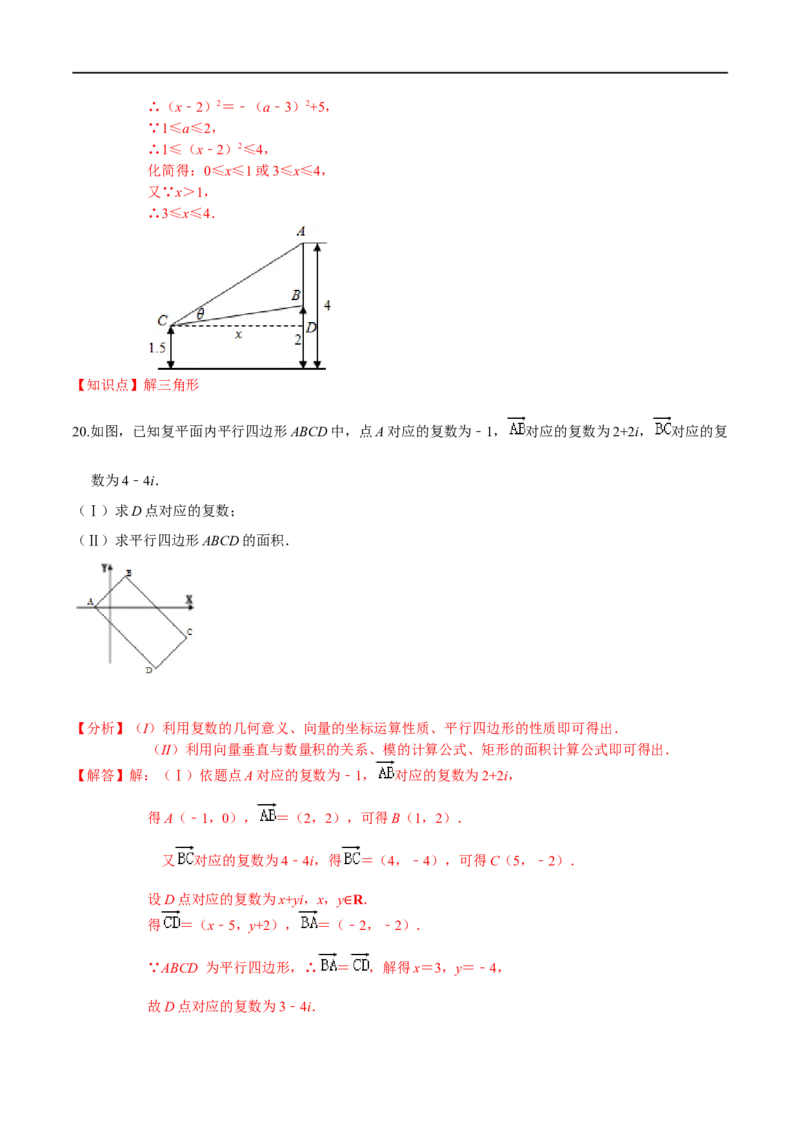
20.如图,已知复平面内平行四边形ABCD中,点A对应的复数为﹣1, 对应的复数为2+2i, 对应的复
数为4﹣4i.
(Ⅰ)求D点对应的复数;
(Ⅱ)求平行四边形ABCD的面积.
【分析】(I)利用复数的几何意义、向量的坐标运算性质、平行四边形的性质即可得出.
(II)利用向量垂直与数量积的关系、模的计算公式、矩形的面积计算公式即可得出.
【解答】解:(Ⅰ)依题点A对应的复数为﹣1, 对应的复数为2+2i,
得A(﹣1,0), =(2,2),可得B(1,2).
又 对应的复数为4﹣4i,得 =(4,﹣4),可得C(5,﹣2).
设D点对应的复数为x+yi,x,y R.
得 =(x﹣5,y+2), =(﹣2,﹣2).
∈
∵ABCD 为平行四边形,∴ = ,解得x=3,y=﹣4,
故D点对应的复数为3﹣4i.(Ⅱ) =(2,2), =(4,﹣4),
可得: =0,∴ .
又| |=2 , =4 .
故平行四边形ABCD的面积= =16.
【知识点】复数的代数表示法及其几何意义
21.如图所示,等腰梯形ABFE是由正方形ABCD和两个全等的Rt△FCB和Rt△EDA组成,AB=1,CF=
2.现将Rt△FCB沿BC所在的直线折起,点F移至点G,使二面角E﹣BC﹣G的大小为60°.
(1)求四棱锥G﹣ABCE的体积;
(2)求异面直线AE与BG所成角的大小.
【分析】(1)推导出GC⊥BC,EC⊥BC,从而∠ECG=60°.连接DG,推导出DG⊥EF,由BC⊥EF,
BC⊥CG,得BC⊥平面DEG,从而DG⊥BC,进而DG⊥平面ABCE,DG是四棱锥G﹣ABCE的
高,由此能求出四棱锥G﹣ABCE的体积.
(2)取DE的中点H,连接BH、GH,则BH∥AE,∠GBH既是AE与BG所成角或其补角.
由此能求出异面直线AE与BG所成角的大小.
【解答】解:(1)由已知,有GC⊥BC,EC⊥BC,所以∠ECG=60°.
连接DG,由CD=AB=1,CG=CF=2,∠ECG=60°,有DG⊥EF ,
由BC⊥EF,BC⊥CG,有BC⊥平面DEG,所以,DG⊥BC ,
①
由①②知,DG⊥平面ABCE,所以DG就是四棱锥G﹣ABCE的高,
②
在Rt△CDG中, .
故四棱锥G﹣ABCE的体积为:
.
(2)取DE的中点H,连接BH、GH,
则BH∥AE,故∠GBH既是AE与BG所成角或其补角.
在△BGH中, , ,
则 .故异面直线AE与BG所成角的大小为 .
【知识点】异面直线及其所成的角、棱柱、棱锥、棱台的体积
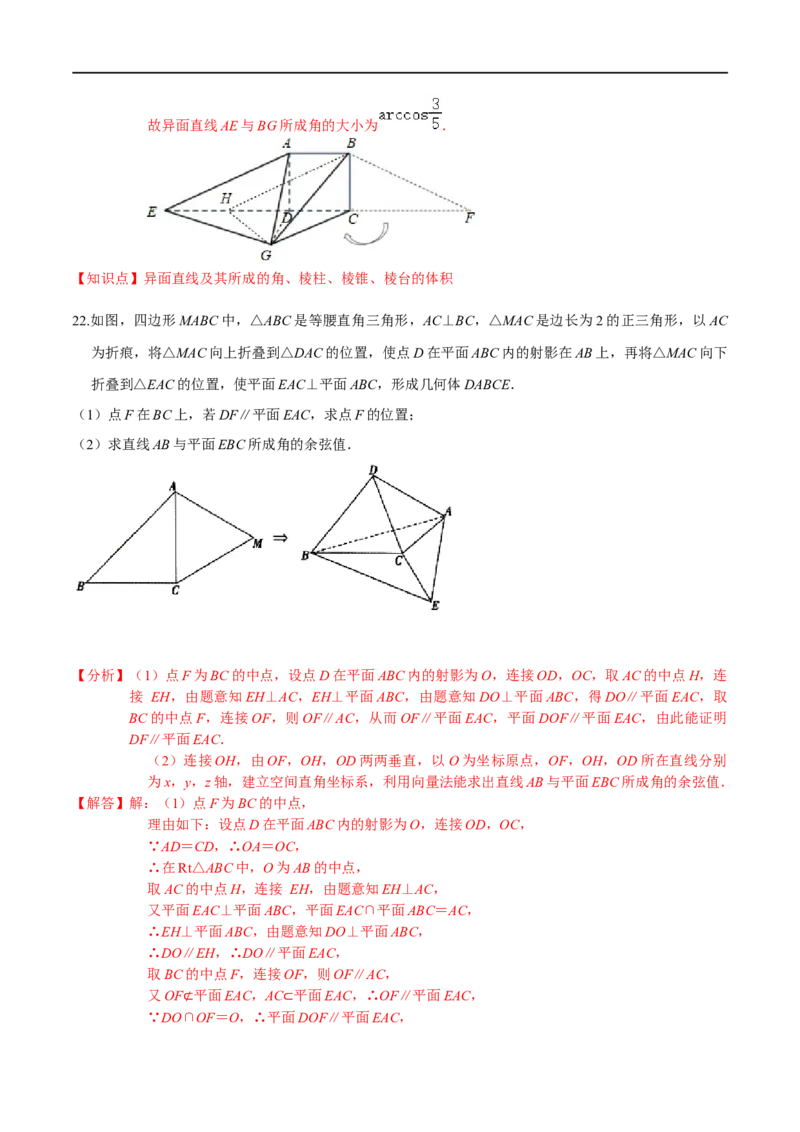
22.如图,四边形MABC中,△ABC是等腰直角三角形,AC⊥BC,△MAC是边长为2的正三角形,以AC
为折痕,将△MAC向上折叠到△DAC的位置,使点D在平面ABC内的射影在AB上,再将△MAC向下
折叠到△EAC的位置,使平面EAC⊥平面ABC,形成几何体DABCE.
(1)点F在BC上,若DF∥平面EAC,求点F的位置;
(2)求直线AB与平面EBC所成角的余弦值.
【分析】(1)点F为BC的中点,设点D在平面ABC内的射影为O,连接OD,OC,取AC的中点H,连
接 EH,由题意知EH⊥AC,EH⊥平面ABC,由题意知DO⊥平面ABC,得DO∥平面EAC,取
BC的中点F,连接OF,则OF∥AC,从而OF∥平面EAC,平面DOF∥平面EAC,由此能证明
DF∥平面EAC.
(2)连接OH,由OF,OH,OD两两垂直,以O为坐标原点,OF,OH,OD所在直线分别
为x,y,z轴,建立空间直角坐标系,利用向量法能求出直线AB与平面EBC所成角的余弦值.
【解答】解:(1)点F为BC的中点,
理由如下:设点D在平面ABC内的射影为O,连接OD,OC,
∵AD=CD,∴OA=OC,
∴在Rt△ABC中,O为AB的中点,
取AC的中点H,连接 EH,由题意知EH⊥AC,
又平面EAC⊥平面ABC,平面EAC∩平面ABC=AC,
∴EH⊥平面ABC,由题意知DO⊥平面ABC,
∴DO∥EH,∴DO∥平面EAC,
取BC的中点F,连接OF,则OF∥AC,
又OF 平面EAC,AC 平面EAC,∴OF∥平面EAC,
∵DO∩OF=O,∴平面DOF∥平面EAC,
⊄ ⊂∵DF 平面DOF,∴DF∥平面EAC.
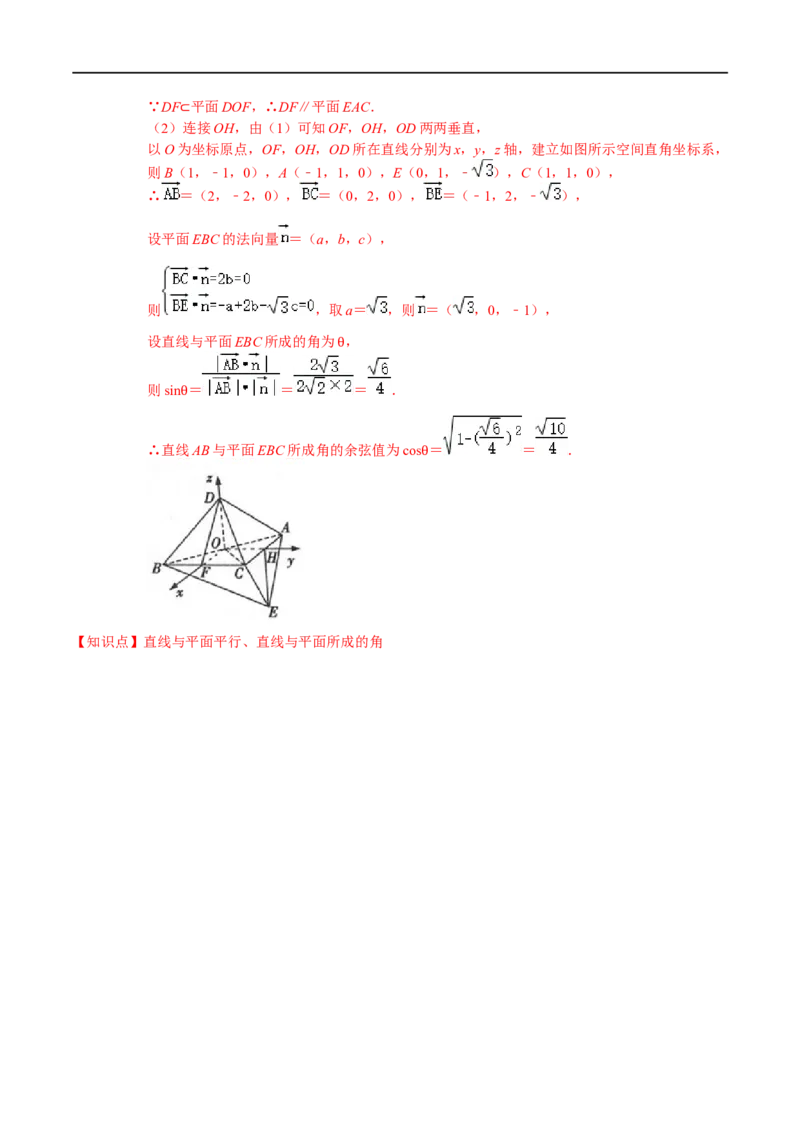
(2)连接OH,由(1)可知OF,OH,OD两两垂直,
⊂
以O为坐标原点,OF,OH,OD所在直线分别为x,y,z轴,建立如图所示空间直角坐标系,
则B(1,﹣1,0),A(﹣1,1,0),E(0,1,﹣ ),C(1,1,0),
∴ =(2,﹣2,0), =(0,2,0), =(﹣1,2,﹣ ),
设平面EBC的法向量 =(a,b,c),
则 ,取a= ,则 =( ,0,﹣1),
设直线与平面EBC所成的角为 ,
θ
则sin = = = .
θ
∴直线AB与平面EBC所成角的余弦值为cos = = .
θ
【知识点】直线与平面平行、直线与平面所成的角