文档内容
期中检测卷 02
姓名:__________________ 班级:______________ 得分:_________________
注意事项:
本试卷满分150分,考试时间120分钟,试题共22题.答卷前,考生务必用0.5毫米黑色签字笔将自
己的姓名、班级等信息填写在试卷规定的位置.
一、选择题(本大题共8小题,每小题5分,共40分)在每小题所给出的四个选项中,只有一项是符合题
目要求的.
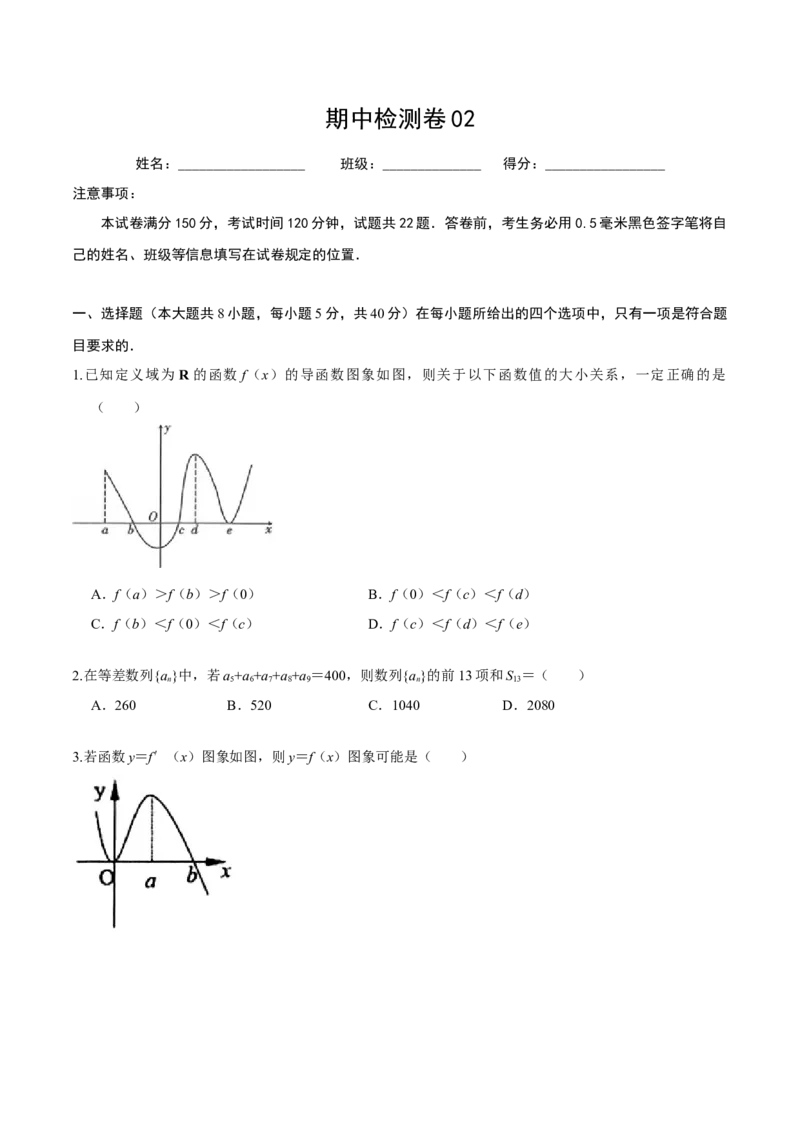
1.已知定义域为 R的函数 f(x)的导函数图象如图,则关于以下函数值的大小关系,一定正确的是
( )
A.f(a)>f(b)>f(0) B.f(0)<f(c)<f(d)
C.f(b)<f(0)<f(c) D.f(c)<f(d)<f(e)
2.在等差数列{a}中,若a+a+a+a+a=400,则数列{a}的前13项和S =( )
n 5 6 7 8 9 n 13
A.260 B.520 C.1040 D.2080
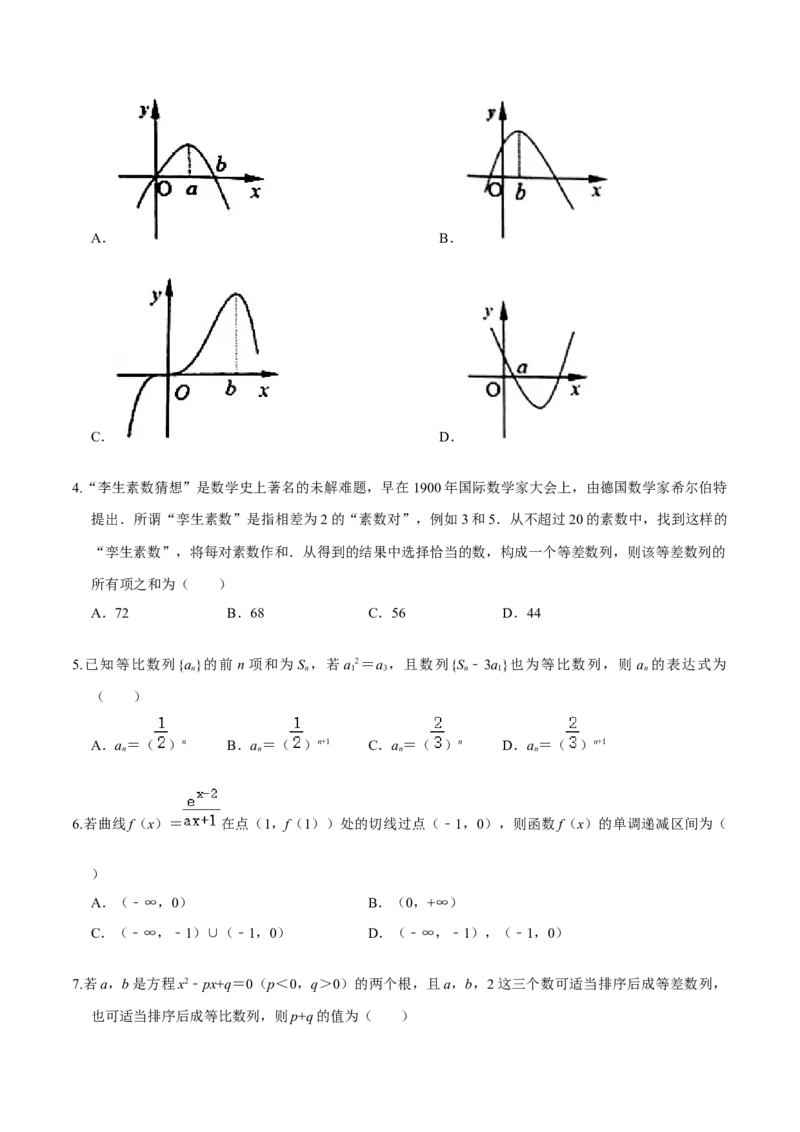
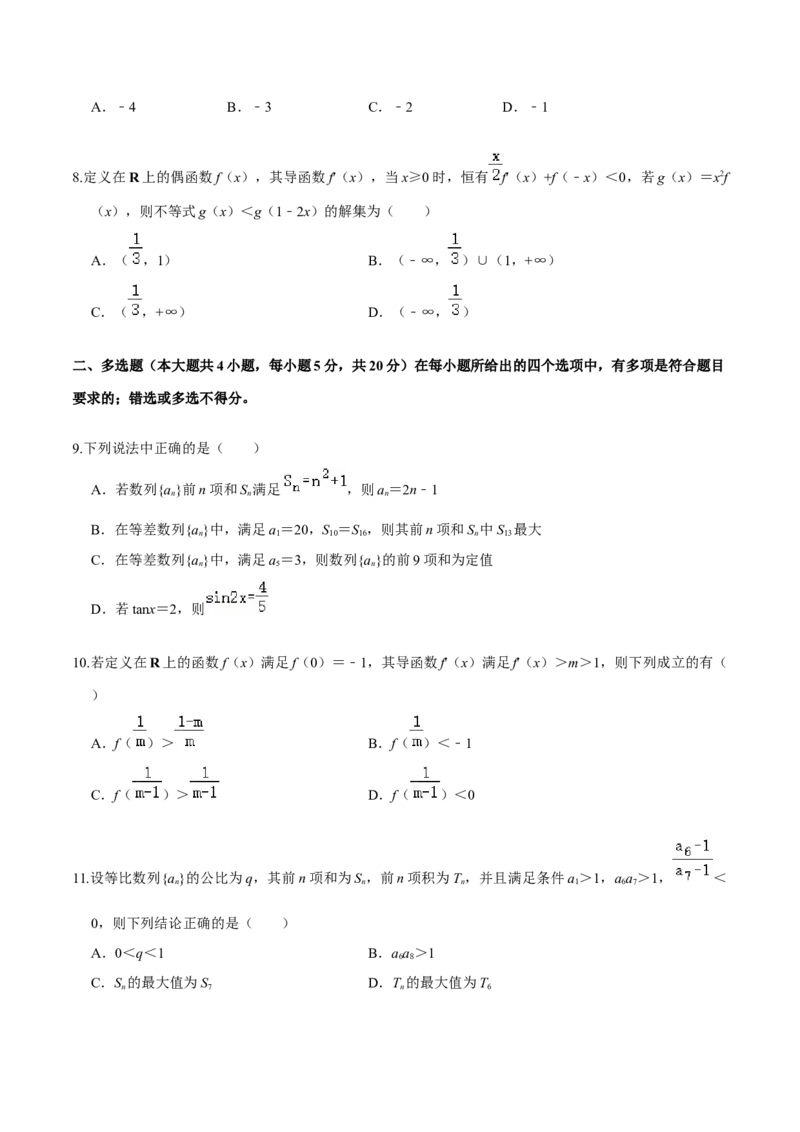
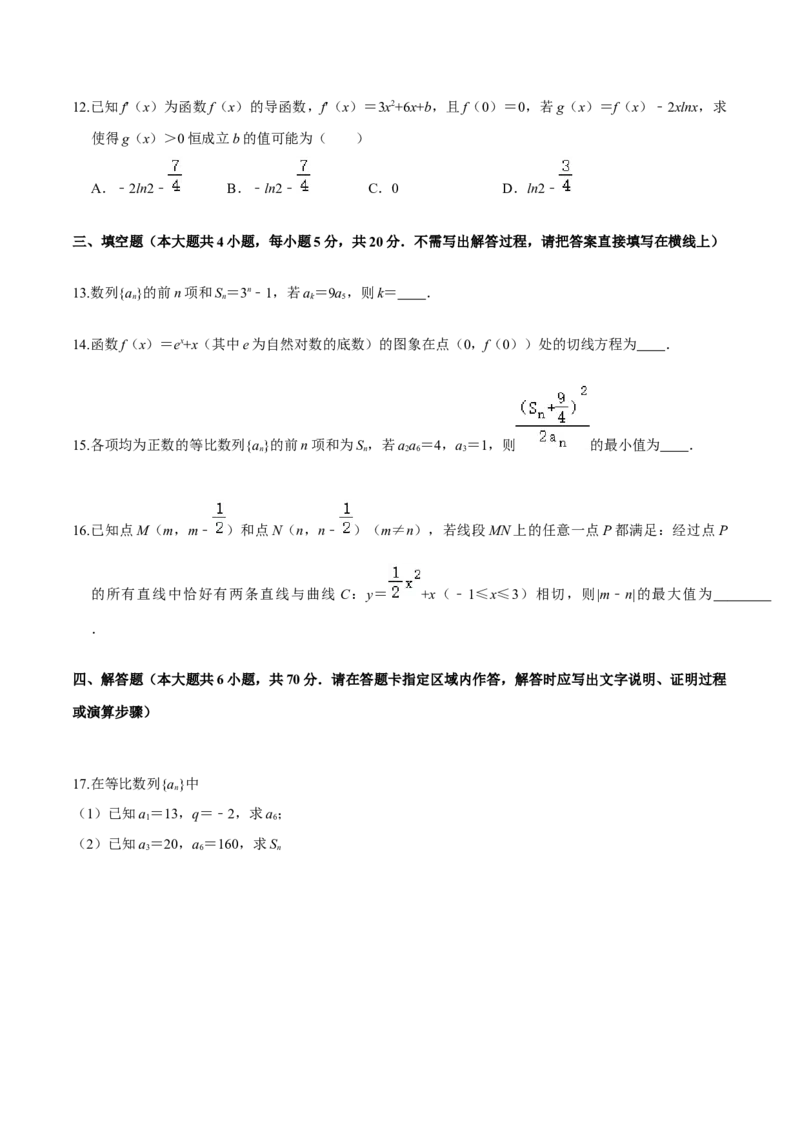
3.若函数y=f′(x)图象如图,则y=f(x)图象可能是( )A. B.
C. D.
4.“李生素数猜想”是数学史上著名的未解难题,早在1900年国际数学家大会上,由德国数学家希尔伯特
提出.所谓“孪生素数”是指相差为2的“素数对”,例如3和5.从不超过20的素数中,找到这样的
“孪生素数”,将每对素数作和.从得到的结果中选择恰当的数,构成一个等差数列,则该等差数列的
所有项之和为( )
A.72 B.68 C.56 D.44
5.已知等比数列{a}的前 n 项和为 S ,若 a2=a ,且数列{S﹣3a}也为等比数列,则 a 的表达式为
n n 1 3 n 1 n
( )
A.a=( )n B.a=( )n+1 C.a=( )n D.a=( )n+1
n n n n
6.若曲线f(x)= 在点(1,f(1))处的切线过点(﹣1,0),则函数f(x)的单调递减区间为(
)
A.(﹣∞,0) B.(0,+∞)
C.(﹣∞,﹣1)∪(﹣1,0) D.(﹣∞,﹣1),(﹣1,0)
7.若a,b是方程x2﹣px+q=0(p<0,q>0)的两个根,且a,b,2这三个数可适当排序后成等差数列,
也可适当排序后成等比数列,则p+q的值为( )A.﹣4 B.﹣3 C.﹣2 D.﹣1
8.定义在R上的偶函数f(x),其导函数f'(x),当x≥0时,恒有 f'(x)+f(﹣x)<0,若g(x)=x2f
(x),则不等式g(x)<g(1﹣2x)的解集为( )
A.( ,1) B.(﹣∞, )∪(1,+∞)
C.( ,+∞) D.(﹣∞, )
二、多选题(本大题共4小题,每小题5分,共20分)在每小题所给出的四个选项中,有多项是符合题目
要求的;错选或多选不得分。
9.下列说法中正确的是( )
A.若数列{a}前n项和S 满足 ,则a=2n﹣1
n n n
B.在等差数列{a}中,满足a=20,S =S ,则其前n项和S 中S 最大
n 1 10 16 n 13
C.在等差数列{a}中,满足a=3,则数列{a}的前9项和为定值
n 5 n
D.若tanx=2,则
10.若定义在R上的函数f(x)满足f(0)=﹣1,其导函数f'(x)满足f'(x)>m>1,则下列成立的有(
)
A.f( )> B.f( )<﹣1
C.f( )> D.f( )<0
11.设等比数列{a}的公比为q,其前n项和为S ,前n项积为T ,并且满足条件a >1,aa >1, <
n n n 1 6 7
0,则下列结论正确的是( )
A.0<q<1 B.aa>1
6 8
C.S 的最大值为S D.T 的最大值为T
n 7 n 612.已知f'(x)为函数f(x)的导函数,f'(x)=3x2+6x+b,且f(0)=0,若g(x)=f(x)﹣2xlnx,求
使得g(x)>0恒成立b的值可能为( )
A.﹣2ln2﹣ B.﹣ln2﹣ C.0 D.ln2﹣
三、填空题(本大题共4小题,每小题5分,共20分.不需写出解答过程,请把答案直接填写在横线上)
13.数列{a}的前n项和S=3n﹣1,若a=9a,则k= .
n n k 5
14.函数f(x)=ex+x(其中e为自然对数的底数)的图象在点(0,f(0))处的切线方程为 .
15.各项均为正数的等比数列{a}的前n项和为S,若aa=4,a=1,则 的最小值为 .
n n 2 6 3
16.已知点M(m,m﹣ )和点N(n,n﹣ )(m≠n),若线段MN上的任意一点P都满足:经过点P
的所有直线中恰好有两条直线与曲线 C:y= +x(﹣1≤x≤3)相切,则|m﹣n|的最大值为
.
四、解答题(本大题共6小题,共70分.请在答题卡指定区域内作答,解答时应写出文字说明、证明过程
或演算步骤)
17.在等比数列{a}中
n
(1)已知a=13,q=﹣2,求a;
1 6
(2)已知a=20,a=160,求S
3 6 n18.设函数
(Ⅰ)讨论f(x)的单调性;
(Ⅱ)求f(x)在区间[﹣2,2]的最大值和最小值.
19.已知函数f(x)= 是定义域上的奇函数,且f(﹣1)=﹣2.
(1)求函数f(x)的解析式,判断函数f(x)在(0,+∞)上的单调性并证明;
(2)令h(x)=ln[f(x)﹣x+a],设a>0,若对任意b [ ,1],当x ,x [b,b+1]时,都有|h(x )﹣h
1 2 1
(x)|≤ln4,求实数a的取值范围. ∈ ∈
2
20.已知函数f(x)=alnx﹣2ax+ (a>0).
(1)讨论f(x)的单调性;
(2)若f(x)有两个极值点x、x(x≠x),且不等式 恒成立,求实数
1 2 1 2
λ
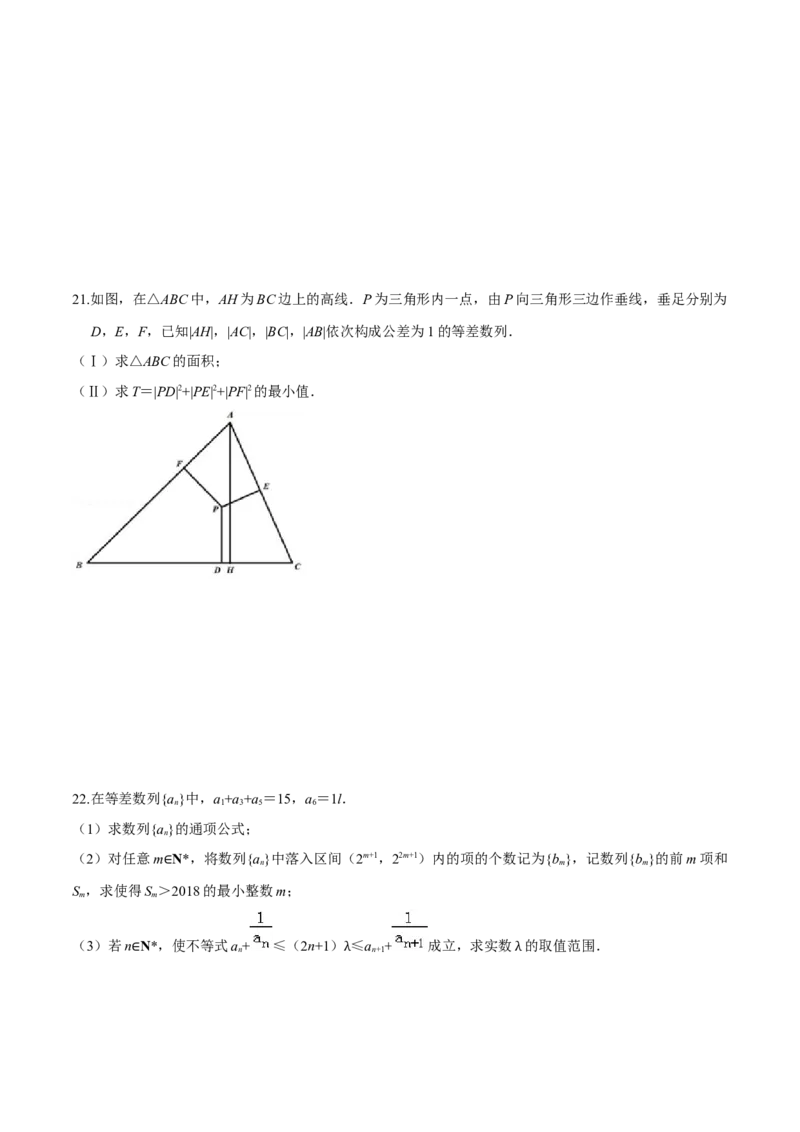
的取值范围.21.如图,在△ABC中,AH为BC边上的高线.P为三角形内一点,由P向三角形三边作垂线,垂足分别为
D,E,F,已知|AH|,|AC|,|BC|,|AB|依次构成公差为1的等差数列.
(Ⅰ)求△ABC的面积;
(Ⅱ)求T=|PD|2+|PE|2+|PF|2的最小值.
22.在等差数列{a}中,a+a+a=15,a=1l.
n 1 3 5 6
(1)求数列{a}的通项公式;
n
(2)对任意m N*,将数列{a}中落入区间(2m+1,22m+1)内的项的个数记为{b },记数列{b }的前m项和
n m m
S ,求使得S >∈2018的最小整数m;
m m
(3)若n N*,使不等式a+ ≤(2n+1) ≤a + 成立,求实数 的取值范围.
n n+1
∈ λ λ