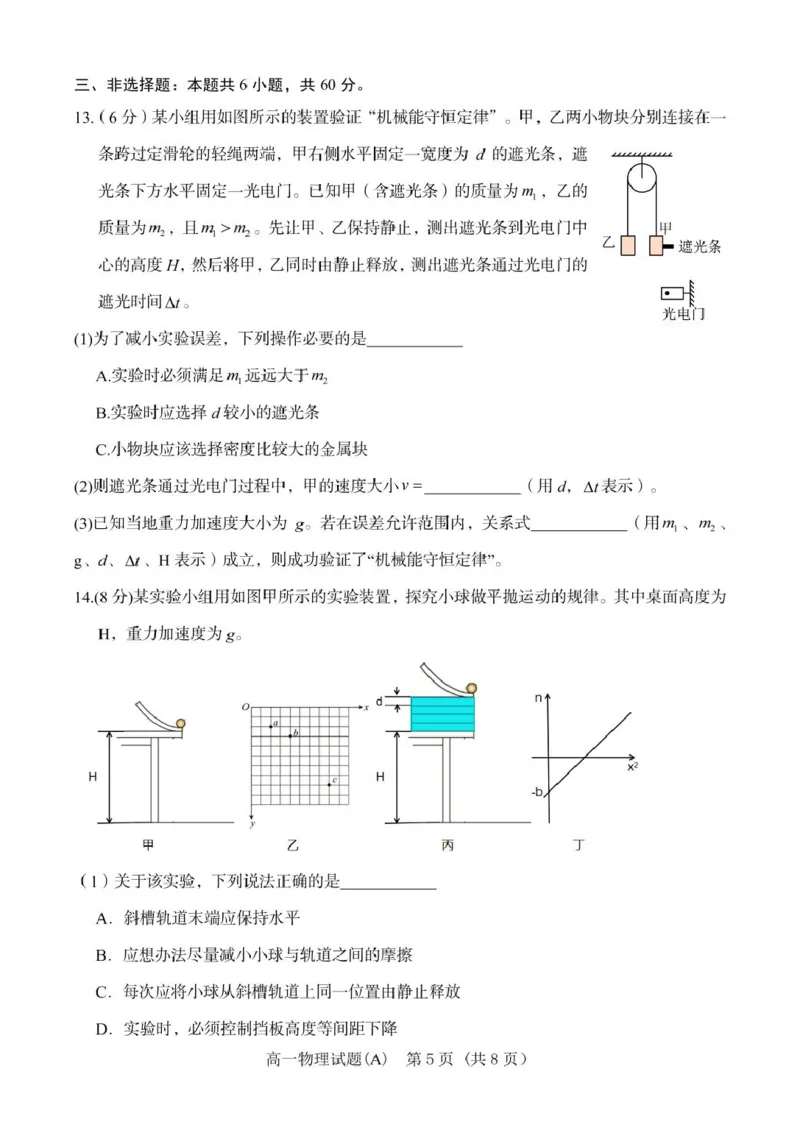
文档内容
2025 年高一 3 月校际联考 物 理 试 题答案
1
2
3
4
5
6
7
8
9
10
11
12
C
D
A
C
B
A
B
D
AD
AC
BD
AD
三、非选择题:本题共 6 小题,共 60 分。
13. (6 分)【答案】(1)BC
(2)
(3)
【详解】(1)A.只要使得
,使甲加速下落即可,故 A 错;
B.实验时应选择 d 较小的遮光条,减小速度计算的误差,故 B 对;
C.小物块应该选择密度比较大的金属块,减小空气阻力带来的影响,故 C 对。故选 BC。
(2)遮光条通过光电门过程中,甲的速度大小为
(3)对甲(含遮光条)和乙组成的系统,从静止释放开始到遮光条通过光电门的整个过程中,重力势能的
减少量
动能的增加量
要使系统机械能守恒,需要满足
即
14.(8 分)【答案】(1)
AC
5L
【详解】(1)A.为保证小球初速度水平,斜槽轨道末端应保持水平,故 A 正确;
B.小球与轨道之间的摩擦对实验结果无影响,故 B 错误;
C.为保证小球初速度相等,每次应将小球从斜槽轨道上同一位置由静止释放,故 C 正确;
D.挡板高度无需等间距下降,故 D 错误;故选 AC。
(2)根据水平方向做匀速直线运动可知相邻两点的水平距离相等,竖直方向满足
设 d 点的纵坐标为
,则
解得
(3)水平方向
竖直方向
1
所以
,可得
,
。所以
,
15.(8 分)答案:(1)15m/s(2)1.69J
(1)甲拍出球后,球做平抛运动:
(1 分)
∴
球碰地后反弹到被乙接住有,
(1 分)
∴
球水平方向做匀速直线运动,有
(1 分)
∴
(1 分)
(2)排球损失的机械能
(2 分)
∴
(2 分)
16.(8 分)答案:(1)5m/s(2)4s(3) m/
解析:(1)当货物达到最大速度时,牵引力 F 与浮力 F 浮、阻力 f 和重力 mg 平衡,
(1 分)
又因为
(1 分)
联立可得:
(1 分)
(2)货物匀加速启动时,由牛顿第二定律
(1 分)
所以
功率达到额定功率时,结束匀加速运动:
所以
(1 分)
可得
(1 分)
(3)速度 v= 4.5m/s 时,因为速度大于匀加速运动的末速度,所以此时的功率为额定功率。根据 P = Fv ,
可得此时牵引力
又因为
(1 分)
可得
m/
(1 分)
17、(14 分)答案:(1)8J (2)23.86J (3)9.34 J
解析:(1)物理先受到滑动摩擦力沿传送带向上匀加速,由牛顶第二定律得
(1 分)
可得
设物体向上运动的位移为 S1 时与传送带共速,由运动学公式
(1 分)
可得 S1=1.25m
2
设此过程中所用的时间为 t,则有 S1=
(1 分)
而传送带的位移
物块与传送带的相对位移
(1 分)
物体由 A 运动至 C 过程中与传送带之间产生的热量 Q=
(1 分)
求得 Q=8J
(1 分)
(2)由几何知识可得,AC 间的高度为
由功能关系可得,物体由 A 运动至 C 过程中由于带动物体运动,电动机对传送带多做的功
W1
(2 分)
代入数据可得,W1=23.86J
(1 分)
(3)由于 CB=OC=l0=1.6m
所以 OB 与传送带的夹角
(1 分)
物体在 B 点静止,设此时橡皮筋的拉力为 F,由受力平衡可得
(1 分)
计算可得 F=0.34N
OB 间的距离 l=2×l0cosα=3.04m
此时橡皮筋的伸长量Δl=l-l0=3.04-1.6=1.44m
由胡克定律可得:F=k Δx (1 分)
物体由 C 到 B,由动能定理可得:
(1 分)
物体由 C 运动至 B 的整个过程中,传送带对物体的摩擦力做的功 w2=9.34 J (1 分)
18、答案:(1)16J (2)228N/m
(3)
(1)滑块 P 从开始运动到刚好沿轨道上升到 B 处,由动能定理得
(2 分)
解得 W=16J
(1 分)
(2)设滑块 P 滑上木板的速度大小为 vc,滑上木板之后,对木板和滑块 Q:
(1 分)
得,
对滑块 P 有,
(1 分)
得,
设经过时间 t 滑块 P 和木板共速,共同速度设为 v,则有
(1 分)
因为 P、Q 恰好不相撞,所以,P 和木板的相对位移等于板长,即
(1 分)
3
可得
设滑块 P 离开弹簧时的速度为
,从滑块 P 离开弹簧到冲到 C 点,由动能定理有
(1 分)
可得
滑块 P 压缩弹簧至最低点时,设弹簧的压缩量为 x,由受力平衡得
(1 分)
撤去推力,滑块 P 上升到离开弹簧的过程中,由动能定理
(1 分)
代入数据可得:k=228N/m (1 分)
(3)滑块 P 滑上木板与模板共速之后一起减速,共同的加速度满足
(1 分)
设滑块 P 以
滑上木板后,之后以速度
与木板共速,最终恰能使得 Q 触发到 E,则有
(1 分)
(1 分)
联立可得:
从最低点到 C 点的过程,由动能定理得
(1 分)
解得,
(1 分)
4