文档内容
2024-2025 学年山东省名校联盟高一下学期 3 月校际联考数学试卷
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.已知向量 ⃗ ⃗ ,则 ⃗ ( )
AB=(−2,1),AC=(3,4) BC=
A. (1,5) B. (−1,−5) C. (−5,−3) D. (5,3)
2i
2.已知i是虚数单位,则 =( )
1+i
A. 1+i B. 1−i C. −1−i D. −1+i
π
3.在▵ABC中,已知AB=1,AC=2,∠BAC= ,则▵ABC的面积为( )
3
√3
A. B. √3 C. 1 D. 2
2
4.在▵ABC中,D在线段BC上,AD为∠BAC的角平分线,若AB=2AC,则( )
⃗ 1 ⃗ 3 ⃗ ⃗ 3 ⃗ 1 ⃗
A. AD= AB+ AC B. AD= AB+ AC
4 4 4 4
⃗ 1 ⃗ 2 ⃗ 2 1
C. AD= AB+ AC D. ⃗AD= ⃗AB+ ⃗AC
3 3 3 3
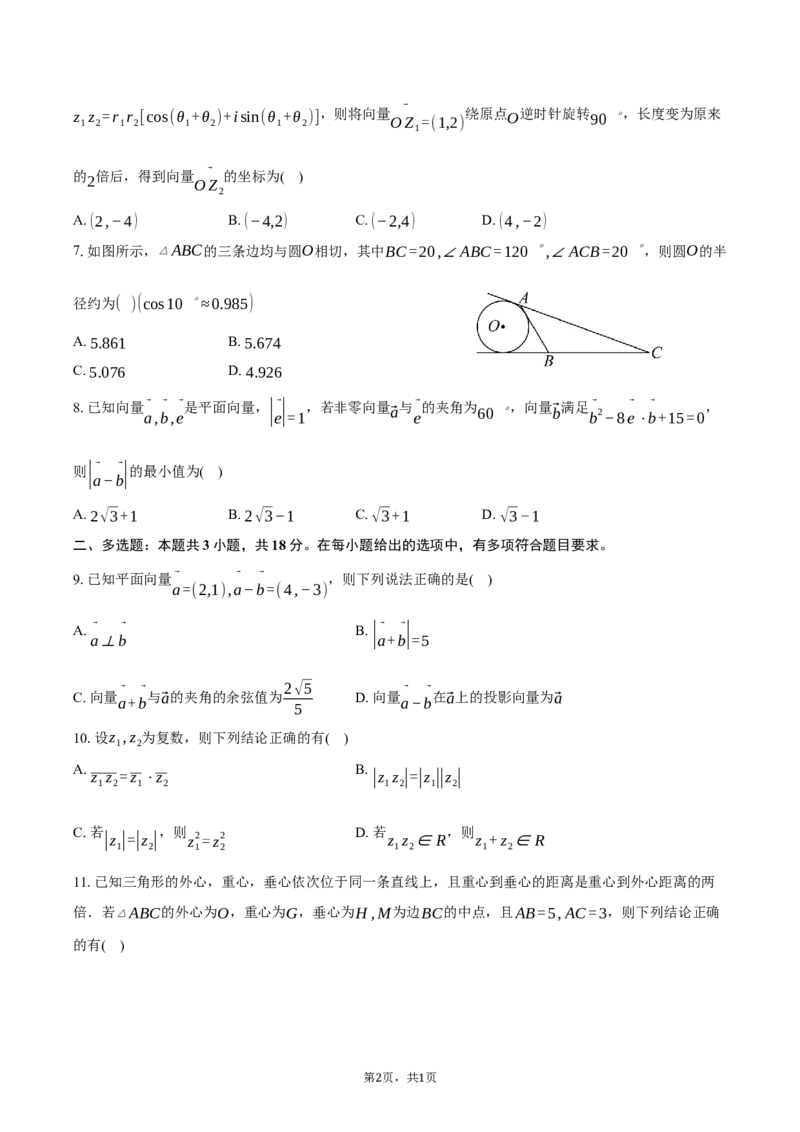
5.如图,在测量河对岸的塔高AB时,可以选取与塔底B在同一水平面内的两个测量基点C,D.现测得
∠BCD=α,∠BDC=β,CD=l,在点C测得塔顶A的仰角为θ,则塔高AB=( )
l⋅tanθsinβ l⋅tanθsin(α+β) l⋅sinθsin(α+β)
A. B. C.
sin(α+β) sinβ sinβ
l⋅sinθsinβ
D.
sin(α+β)
6.已知复数 可以表示为 ,其中 , 是以 轴非负半轴为
z=a+bi(a,b∈R) z=r(cosθ+isinθ) r=√a2+b2 θ x
始边,向量⃗OZ所在射线为终边的角.已知z =r (cosθ +isinθ )与z =r (cosθ +isinθ )的乘积
1 1 1 1 2 2 2 2
第 页,共 页
1 1z 1 z 2 =r 1 r 2 [cos(θ 1 +θ 2 )+isin(θ 1 +θ 2 )] ,则将向量 O ⃗ Z =(1,2) 绕原点 O 逆时针旋转 90 ∘,长度变为原来
1
的 2 倍后,得到向量 ⃗ 的坐标为( )
OZ
2
A. (2,−4) B. (−4,2) C. (−2,4) D. (4,−2)
7.如图所示,▵ABC的三条边均与圆O相切,其中BC=20,∠ABC=120 ∘,∠ACB=20 ∘,则圆O的半
径约为( )(cos10 ∘≈0.985)
A. 5.861 B. 5.674
C. 5.076 D. 4.926
8.已知向量⃗
a,
⃗
b,
⃗
e
是平面向量,|⃗
e
|
=1
,若非零向量
⃗a
与⃗
e
的夹角为
60
∘,向量⃗b 满足⃗
b2−8
⃗
e⋅
⃗
b+15=0
,
则|⃗ ⃗|的最小值为( )
a−b
A. 2√3+1 B. 2√3−1 C. √3+1 D. √3−1
二、多选题:本题共3小题,共18分。在每小题给出的选项中,有多项符合题目要求。
9.已知平面向量⃗ ⃗ ⃗ ,则下列说法正确的是( )
a=(2,1),a−b=(4,−3)
A. ⃗ ⃗ B. |⃗ ⃗|
a⊥b a+b =5
2√5
⃗ ⃗ ⃗ ⃗
C. 向量 a+b 与⃗a的夹角的余弦值为 D. 向量 a−b 在⃗a上的投影向量为⃗a
5
10.设z ,z 为复数,则下列结论正确的有( )
1 2
A. B.
z z =z ⋅z |z z |=|z ||z |
1 2 1 2 1 2 1 2
C. 若 ,则 D. 若 ,则
|z |=|z | z2=z2 z z ∈R z +z ∈R
1 2 1 2 1 2 1 2
11.已知三角形的外心,重心,垂心依次位于同一条直线上,且重心到垂心的距离是重心到外心距离的两
倍.若▵ABC的外心为O,重心为G,垂心为H,M为边BC的中点,且AB=5,AC=3,则下列结论正确
的有( )
第 页,共 页
2 1⃗ ⃗ 16
A. AG⋅BC=−
3
B.
A
⃗
O⋅B
⃗
C=8
C. ⃗ ⃗ ⃗ ⃗ D. ⃗ ⃗ ⃗ ⃗
OH=OA+OB+OC AB+AC=4OM+2HM
三、填空题:本题共3小题,每小题5分,共15分。
12.已知i为虚数单位,若复数z=(1+i)(a−2i)(a∈R)为纯虚数,则a的值为 .
⃗ ⃗
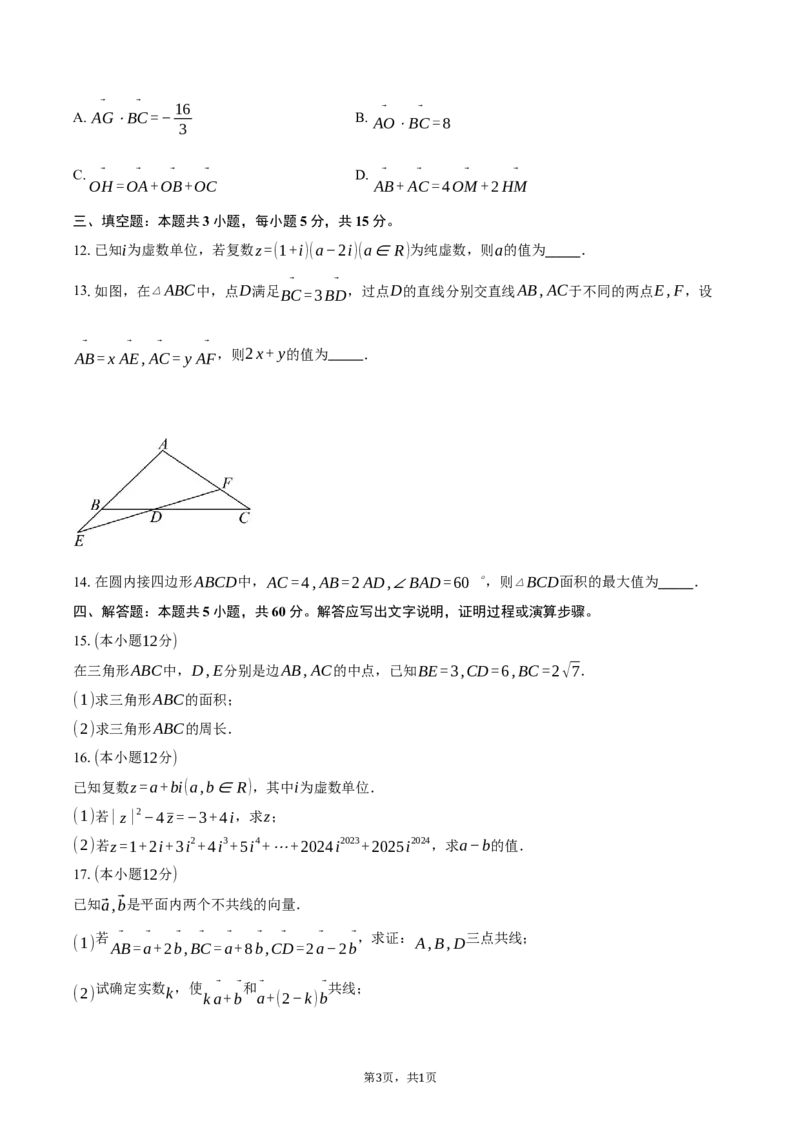
13.如图,在▵ABC中,点D满足
BC=3BD
,过点D的直线分别交直线AB,AC于不同的两点E,F,设
A ⃗ B=x A ⃗ E,A ⃗ C= y A ⃗ F ,则2x+ y的值为 .
14.在圆内接四边形ABCD中,AC=4,AB=2AD,∠BAD=60 ∘,则▵BCD面积的最大值为 .
四、解答题:本题共5小题,共60分。解答应写出文字说明,证明过程或演算步骤。
15.(本小题12分)
在三角形ABC中,D,E分别是边AB,AC的中点,已知BE=3,CD=6,BC=2√7.
(1)求三角形ABC的面积;
(2)求三角形ABC的周长.
16.(本小题12分)
已知复数z=a+bi(a,b∈R),其中i为虚数单位.
(1)若|z|2−4z=−3+4i,求z;
(2)若z=1+2i+3i2+4i3+5i4+⋯+2024i2023+2025i2024,求a−b的值.
17.(本小题12分)
已知⃗a,⃗b是平面内两个不共线的向量.
若 ⃗ ⃗ ⃗ ⃗ ⃗ ⃗ ⃗ ⃗ ⃗,求证: 三点共线;
(1)
AB=a+2b,BC=a+8b,CD=2a−2b
A,B,D
试确定实数 ,使 ⃗ ⃗和⃗ ⃗共线;
(2) k ka+b a+(2−k)b
第 页,共 页
3 1(3) 若⃗
a=(2,1),
⃗
b=(−3,2),
(⃗
a+
⃗
b
)
⊥
(
m
⃗
a−
⃗
b
),求实数 m 的值.
18.(本小题12分)
已知三角形ABC的内角A,B,C的对边分别是a,b,c,且满足acosC+√3asinC=b+c.
(1)求角A的大小;
(2)若三角形ABC的面积为10,内切圆的半径为1,求a;
(3)若∠BAC的角平分线交BC于D,且AD=4,求三角形ABC面积的最小值.
19.(本小题12分)
n个有次序的实数⃗
a ,
⃗
a ,⋅⋅⋅,
⃗
a
所组成的有序数组(⃗
a ,
⃗
a ,⋅⋅⋅,
⃗
a
)称为一个 ⃗n维向量,其中
1 2 n 1 2 n
⃗
a
(
i=1,2⋅⋅⋅,
⃗
n
)称为该向量的第i个分量.特别地,对一个 ⃗n维向量⃗
a=
(⃗
a ,
⃗
a ,⋅⋅⋅,
⃗
a
),若
i 1 2 n
|⃗
a
|
=1,i=1,2⋅⋅⋅
⃗
n
,称 ⃗a为 ⃗n维信号向量.设⃗
a=
(⃗
a ,
⃗
a ,⋅⋅⋅,
⃗
a
)
,
⃗
b=
(⃗
b ,
⃗
b ,⋅⋅⋅,
⃗
b
),则 ⃗a和⃗b 的内积
i 1 2 n 1 2 n
定义为⃗ a⋅ ⃗ b=∑ n ⃗ a
i
⃗ b
i
,且⃗
a⊥
⃗
b⇔
⃗
a⋅
⃗
b=0
.
i=1
(1)直接写出4个两两垂直的4维信号向量.
(2)证明:不存在14个两两垂直的14维信号向量.
(3) 已知 k 个两两垂直的 2024 维信号向量⃗
x ,
⃗
x ,⋅⋅⋅,
⃗
x
满足它们的前 m 个分量都是相同的,求证:
1 2 k
√km<45.
第 页,共 页
4 1参考答案
1.D
2.A
3.A
4.C
5.A
6.B
7.C
8.B
9.ABD
10.AB
11.ACD
12.−2
13.3
3√3
14.
2
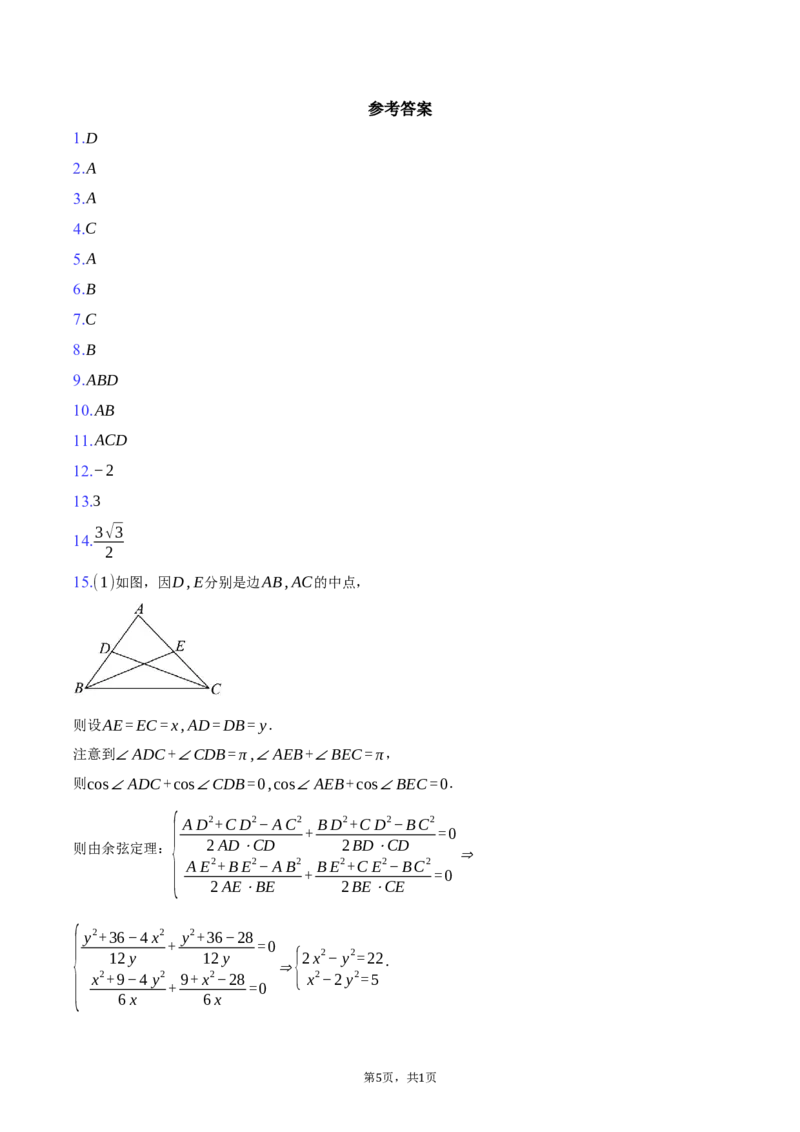
15.(1)如图,因D,E分别是边AB,AC的中点,
则设AE=EC=x,AD=DB= y.
注意到∠ADC+∠CDB=π,∠AEB+∠BEC=π,
则cos∠ADC+cos∠CDB=0,cos∠AEB+cos∠BEC=0.
{AD2+CD2−AC2 BD2+CD2−BC2
+ =0
则由余弦定理: 2AD⋅CD 2BD⋅CD
⇒
AE2+BE2−AB2 BE2+CE2−BC2
+ =0
2AE⋅BE 2BE⋅CE
{y2+36−4x2 y2+36−28
+ =0
12y 12y {2x2−y2=22.
⇒
x2+9−4 y2 9+x2−28 x2−2y2=5
+ =0
6x 6x
第 页,共 页
5 1解得{x=√13 则在三角形 中, .
. ABC AC=2√13,AB=4,BC=2√7
y=2
AB2+AC2−BC2 16+52−28 5√13
由余弦定理可得cosA= = = ,
2AB⋅AC 2×4×2√13 26
3√39
从而sin A=√1−cos2A= .
26
1 1 3√39
则三角形ABC的面积为: AB⋅ACsin A= ×4×2√13× =6√3;
2 2 26
(2)由(1)易得三角形ABC的周长为AB+AC+BC=4+2√13+2√7
16.(1)首先,复数的模长平方∣z∣2=a2+b2,共轭复数z=a−bi.
代入方程得: ,
a2+b2−4(a−bi)=−3+4i
展开并整理实部和虚部: ,
(a2+b2−4a)+4bi=−3+4i
根据复数相等的条件,得到两个方程:{a2+b2−4a=−3
,
4b=4
解得b=1,代入第一个方程:
,
a2+1−4a=−3,a2−4a+4=0,∴(a−2) 2=0,∴a=2
因此,复数z=2+i;
2024
考虑 .
(2) S=∑(n+1)in
n=0
2024 2025
则 .
iS=∑(n+1)in+1=∑ nin
n=0 n=1
2024
相减得:
S−iS=1+∑in−2025i2025
n=1
其中,
2024 i(1−i2024)
因为 ,且 。
∑in= =0( i2024=1) i2025=i
1−i
n=1
因此:S(1−i)=1−2025i
第 页,共 页
6 11−2025i (1−2025i)(1+i) 2026−2024i
解得:S= = = =1013−1012i,
1−i 2 2
因此,z=1013−1012i,即a=1013,b=−1012,
故a−b=1013−(−1012)=2025.
17. ⃗ ⃗ ⃗ ⃗ (⃗ ⃗) (⃗ ⃗) ( ⃗ ⃗) ⃗ ⃗,
(1)AD=AB+BC+CD= a+2b + a+8b + 2a−2b =4a+8b
所以 ⃗ ⃗ ⃗ (⃗ ⃗) ⃗ ,则有 ⃗ ⃗ ,
AD=4a+8b=4 a+2b =4AB AD//AB
又AD与AB 有公共点A,因此A,B,D 三点共线.
(2)
由于
v
⃗ 和
v
⃗ 共线,存在实数
λ
使得:
v
⃗
=λv
⃗
1 2 1 2
⃗ ⃗和⃗ ⃗共线,有 ⃗ ⃗ ⃗ ⃗,
ka+b a+(2−k)b ka+b=λa+λ(2−k)b
则有{ k=λ ,解得 ,
λ=k=1
1=λ(2−k)
所以k=1.
⃗ ⃗ ,
(3)a=(2,1),b=(−3,2)
则⃗ ⃗ , ⃗ ⃗ ,
a+b=(−1,3) ma−b=m(2,1)−(−3,2)=(2m+3,m−2)
由(⃗ ⃗) ( ⃗ ⃗),
a+b ⊥ma−b
则(⃗ ⃗) ( ⃗ ⃗) ,解得 m=9 .
a+b ⋅ ma−b =(−1)(2m+3)+3(m−2)=0
18.(1)由正弦定理边角互化可得:
acosC+√3asinC=b+c⇒sin AcosC+√3sin AsinC=sinB+sinC
又sinB=sin(A+C),则sin AcosC+√3sin AsinC=sin AcosC+cosAsinC+sinC,
从而√3sin AsinC=cosAsinC+sinC,结合sinC>0,
则 ( π) π π或 π 5π 舍去 .
√3sin A−cosA=1⇒2sin A− =1⇒A− = A− = ( )
6 6 6 6 6
π
故A= .
3
第 页,共 页
7 1(2)因三角形ABC的面积为S=10,内切圆的半径为r=1.
1
则S= (a+b+c)r=10⇒a+b+c=20,则b+c=20−a.
2
1 √3 40√3
又由(1),S= bcsin A= bc=10⇒bc= .
2 4 3
80√3
(20−a) 2− −a2
b2+c2−a2 (b+c) 2−2bc−a2 3 1
则由余弦定理:cosA= = = = .
2bc 2bc 80√3 2
3
400−40a 3
= ⇒80a=800−80√3⇒a=10−√3
化简后可得: 80√3 2 ;
3
(3)如图,过D点做AB,AC垂线,垂足为E,F.
π π
由(1)可得∠BAC= ,则∠BAD=∠CAD= ,
3 6
π π
又由角平分线性质可得DE=DF=ADsin =2,AE=AF=ADcos =2√3
6 6
π
又注意到∠AEF+∠EDF+∠DFA+∠FAE=π,∠AEF=∠DFA= ,
2
2π π π
则∠EDF= ⇒∠EDB+FDC= ,设∠EDB=θ,则∠FDC= −θ.
3 3 3
又 ,则 (π ) 其中 ( π).
DE=DF=2 BE=2tanθ,FC=2tan −θ . θ∈ 0,
3 3
故三角形 面积为:1 √3 [ (π )]
ABC AB⋅ACsin A= (2√3+2tanθ) 2√3+2tan −θ
2 4 3
[ (π )] [ (π ) (π )].
√3(√3+tanθ) √3+tan −θ =√3 3+√3tanθ+√3tan −θ +tanθtan −θ
3 3 3
注意到 (π ) π[ (π )] (π ).
tanθ+tan −θ =tan 1−tanθtan −θ =√3−√3tanθtan −θ
3 3 3 3
则 [ (π )] 要使 最小,则需使 (π )最大.
S=√3 6−2tanθtan −θ . S tanθtan −θ
3 3
第 页,共 页
8 1注意到 (π ) ,则由基本不等式取等条件可得,
tanθ>0,tan −θ >0
3
要使 (π )最大,需满足 (π ) π (π ) 1.
tanθtan −θ tanθ=tan −θ ⇒θ= ,tanθtan −θ ≤
3 3 6 3 3
则 [ (π )] ( 2) 16√3,此时 π,即三角形 为等边三角形.
S=√3 6−2tanθtan −θ ≥√3× 6− = θ= ABC
3 3 3 6
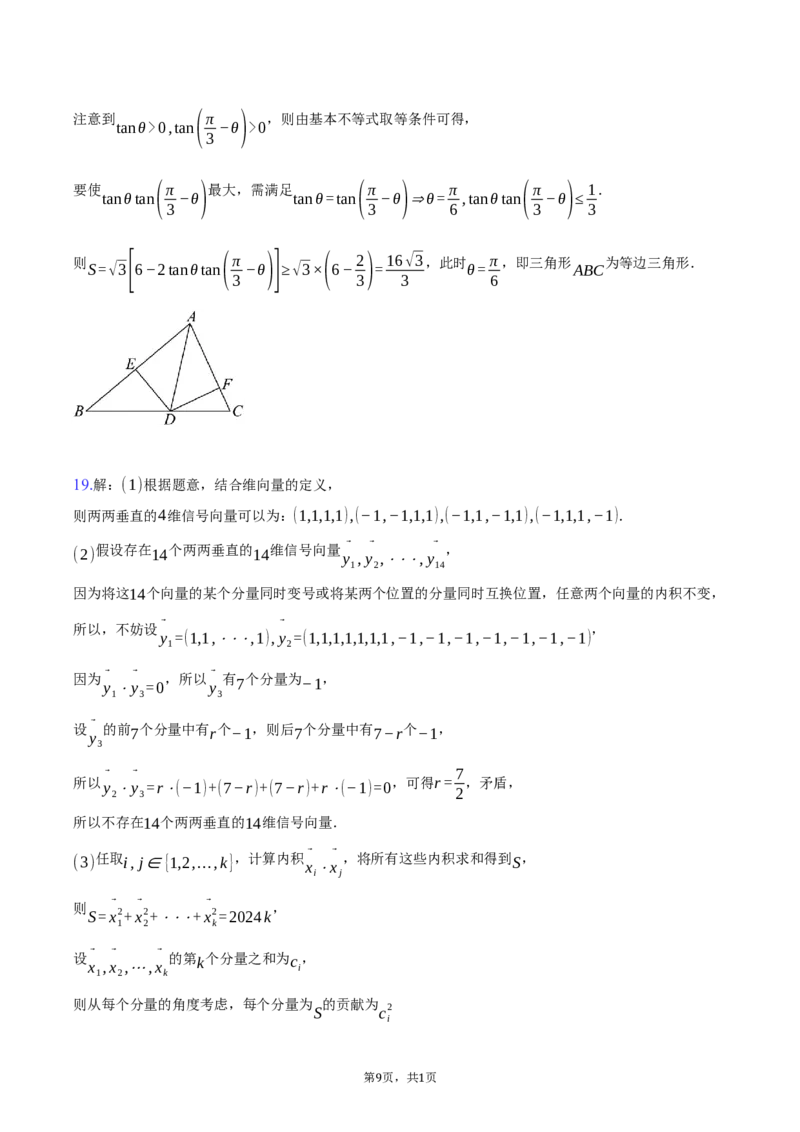
19.解:(1)根据题意,结合维向量的定义,
则两两垂直的4维信号向量可以为:(1,1,1,1),(−1,−1,1,1),(−1,1,−1,1),(−1,1,1,−1).
(2) 假设存在 14 个两两垂直的 14 维信号向量
y
⃗
,y
⃗
,⋅⋅⋅,y
⃗ ,
1 2 14
因为将这14个向量的某个分量同时变号或将某两个位置的分量同时互换位置,任意两个向量的内积不变,
所以,不妨设⃗ ⃗ ,
y =(1,1,⋅⋅⋅,1),y =(1,1,1,1,1,1,1,−1,−1,−1,−1,−1,−1,−1)
1 2
因为⃗ ⃗ ,所以⃗ 有 个分量为 ,
y ⋅y =0 y 7 −1
1 3 3
设⃗ 的前 个分量中有 个 ,则后 个分量中有 个 ,
7 r −1 7 7−r −1
y
3
⃗ ⃗ 7
所以 y ⋅y =r⋅(−1)+(7−r)+(7−r)+r⋅(−1)=0 ,可得r= ,矛盾,
2 3 2
所以不存在14个两两垂直的14维信号向量.
(3) 任取 i, j∈{1,2,…,k} ,计算内积⃗
x⋅
⃗
x
,将所有这些内积求和得到 S ,
i j
则 ⃗ ⃗ ⃗ ,
S=x2+x2+⋅⋅⋅+x2=2024k
1 2 k
设⃗ ⃗ ⃗ 的第
k
个分量之和为c,
x ,x ,⋯,x i
1 2 k
则从每个分量的角度考虑,每个分量为 的贡献为
S c2
i
第 页,共 页
9 1所以 ,
S=c2+c2+⋅⋅⋅+c2 ≥c2+c2+⋅⋅⋅+c2 =k2m
1 2 2024 1 2 m
令2024k≥k2m所以km≤2024<2025,所以√km<45.
第 页,共 页
10 1