文档内容
4.2.2 指数函数的图像和性质
(用时45分钟)
【选题明细表】
知识点、方法 题号
指数函数图像问题 1,2,4
指数函数性质应用 3,5,6,7,10
综合应用 8,9,11,12
基础巩固
1.当 且 时,函数 的图象必经过定点( )
A. B. C. D.
【答案】A
【解析】由函数解析式的特征结合指数函数的性质,令 可得 ,
此时 ,故函数恒过定点 .
故选:A.
2.函数y=2x与y=( )x关于对称( ) .
A.x轴 B.y轴
C.y=x D.原点
【答案】B
【解析】函数y=( )x=2–x,与函数y=2x的图象关于y轴对称,故选B.
3.若f(x)=(2a–1)x是增函数,那么a的取值范围为( ) .
1 1
A.a< B. 1 D.a≥1
【答案】C
【解析】由题意2a-1>1⇒a>1,应选答案C 。
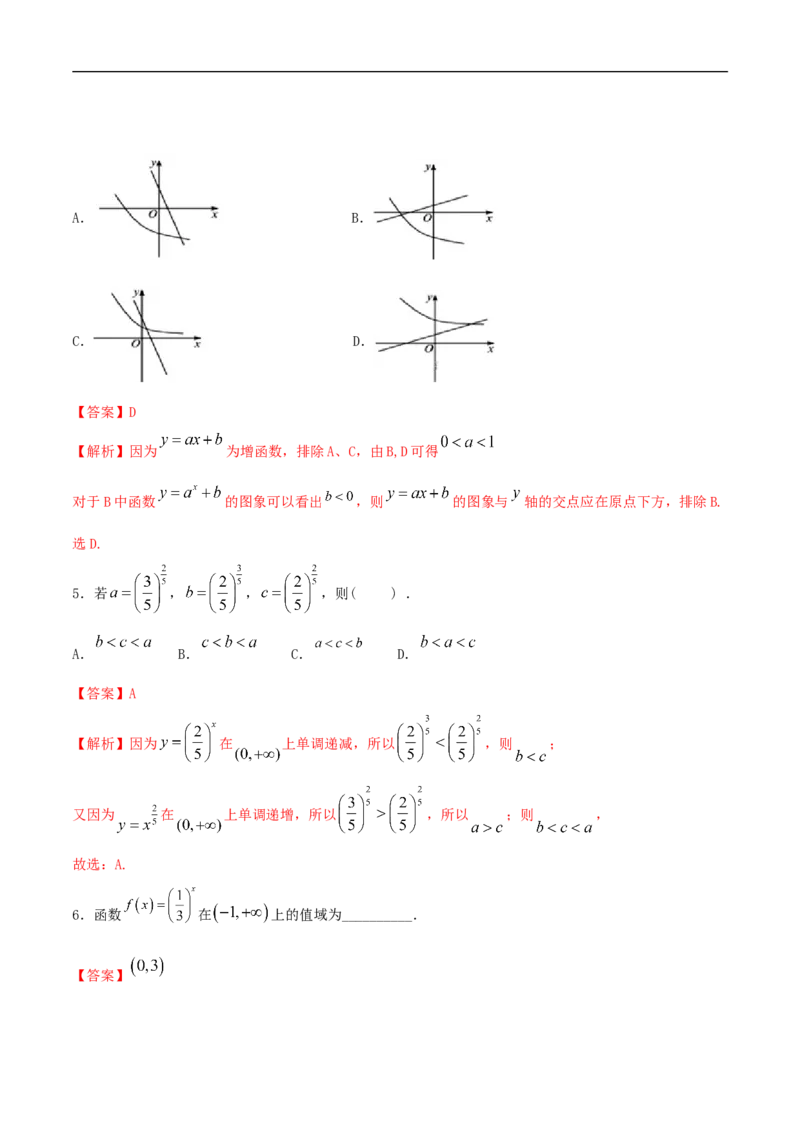
4.函数 与 的图象有可能是( ) .A. B.
C. D.
【答案】D
【解析】因为 为增函数,排除A、C,由B,D可得
对于B中函数 的图象可以看出 ,则 的图象与 轴的交点应在原点下方,排除B.
选D.
5.若 , , ,则( ) .
A. B. C. D.
【答案】A
【解析】因为 在 上单调递减,所以 ,则 ;
又因为 在 上单调递增,所以 ,所以 ;则 ,
故选:A.
6.函数 在 上的值域为__________.
【答案】【解析】因为 在 上单调递减,
所以 时 ,
即 ,
所以函数 在 上的值域为 .故答案为 .
7.函数 的定义域为_______.
【答案】
【解析】由二次根式有意义,得: ,即 ,
因为 在R上是增函数,所以,x≤2,即定义域为:
8.已知函数 的图象经过点 .
(1)求 的值;
(2)求函数 的定义域和值域;
(3)证明:函数 是奇函数.
【答案】(1)1;(2) 的定义域为 ;值域为 ;(3)详见解析.
【解析】(1)由题意知,函数 的图象过点 ,可得 ,解得 .
(2)由(1)知,函数 ,∵ , ,即 的定义域为 .
因为 ,又∵ ,∴ ,所以 的值域为 .
(3)∵ 的定义域为 ,且 ,所以 是奇函数.
能力提升
9.已知函数 ,则不等式 的解集为( )
A. B. C. D.
【答案】B
【解析】可知函数 为减函数,由 ,可得 ,
整理得 ,解得 ,所以不等式的解集为 .
故选B.
10.不等式 的解集是______.
【答案】
【解析】 .
故答案为:
11.已知函数f(x)=a2x+2ax-1(a>1,且a为常数)在区间[-1,1]上的最大值为14.
(1)求f(x)的表达式;
(2)求满足f(x)=7时x的值.
【答案】(1)f(x)=32x+23x-1(2)x=log2
3
【解析】(1)令t=ax >0,∵x∈[-1,1],a>1,∴ax∈[ ,a],f(x)=y=t2+2t-1=(t+1)2-2,
故当t=a时,函数y取得最大值为a2+2a-1=14,求得a=3,
∴f(x)=32x+23x-1.
(2)由f(x)=7,可得32x+2×3x-1=7,
即(3x+4)(3x-2)=0,求得3x=2,∴x=log2.
3
素养达成
12.求函数 的定义域、值域及单调区间.
【答案】定义域是 .值域是 ;单调减区间是 ,单调增区间是 .
【解析】解不等式 ,得 或 ,
所以,函数 的定义域为 .
, ,则函数 的值域为 .
令 ,由二次函数的性质可知,内层函数 在区间 上单调递减,在
区间 上单调递增,外层函数 为增函数,
由复合函数同增异减法可知,函数 的单调递减区间为 ,单调递增区间为 .