文档内容
格致课堂
6.4.1 平面几何中的向量方法
一、选择题
1.在四边形ABCD中,若 ,且| |=| |,则这个四边形是( )
A.平行四边形 B.矩形
C.等腰梯形 D.菱形
2.(2020·全国高一课时练习)已知 是 所在平面内一点,且满足
,则 为
A.等腰三角形 B.直角三角形 C.等边三角形 D.等腰直角三角形
3.(2020·全国高一课时练习)设点M是线段BC的中点,点A在直线BC外,
,则 ( )
A.8 B.4 C.2 D.1
4.(2020·全国高一课时练习) 为平面上的定点,A,B,C是平面上不共线的三点,若
,则 是( )
A.以AB为底面的等腰三角形
B.以BC为底面的等腰三角形
C.以AB为斜边的直角三角形
D.以BC为斜边的直角三角形
⃗a,⃗b,⃗c ⃗a与⃗b
5.(多选题)设 为同一平面内具有相同起点的三个任意的非零向量。且满足 不共线,
⃗a⊥⃗c |⃗a|=|⃗c|
, ,则 的值一定等于( )
⃗a与⃗b
A.以 为邻边的平行四边形的面积
⃗b,⃗c
B.以 为邻边的平行四边形的面积
⃗a与⃗b
C.以 为两边的三角形的面积的2倍;格致课堂
⃗b,⃗c
D.以 为两边的三角形面积。
ΔABC
6.(多选题)点O在 所在的平面内,则以下说法正确的有( )
O⃗A+O⃗B+O⃗C=0⃗ ΔABC
A.若 ,则点O是 的重心。
⃗AC ⃗AB ⃗BC ⃗BA
O⃗A⋅( − )=O⃗B⋅( − )=0
|
⃗AC|
|
⃗AB|
|
⃗BC|
|
⃗BA|
ΔABC
B.若 ,则点O是 的垂心。
(O⃗A+O⃗B)⋅ ⃗AB=(O⃗B+O⃗C)⋅ ⃗BC=0
ΔABC
C.若 ,则点O是 的外心。
O⃗A⋅O⃗B=O⃗B⋅O⃗C=O⃗C⋅O⃗A ΔABC
D.若 ,则点O是 的内心。
二、填空题
7.(2019·全国高一课时练习)已知 是 内一点, ,记 的面积为
, 的面积为 ,则 __________.
8.(2019·全国高一课时练习)若点 是 所在平面内的一点,且满足 ,
则 与 的面积比为__.
9.已知 为△ 的外心,若 + − =0,则 =_____.
10.在四边形ABCD中, =(1,2), =(-4,2),则 与 的夹角为 ,该四
边形的面积为___________.
三.解答题
11.(2020·全国高一课时练习)如图,在正方形 中, 分别为 的中点,求证:
(利用向量证明).格致课堂
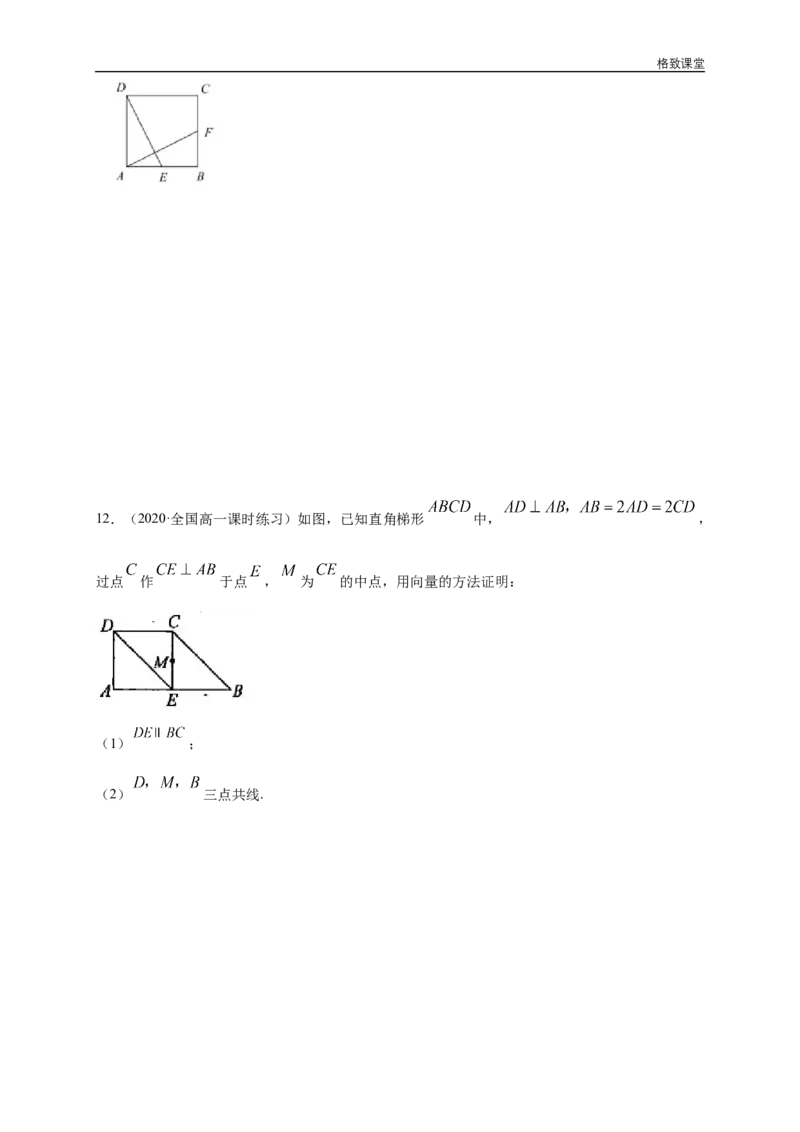
12.(2020·全国高一课时练习)如图,已知直角梯形 中, ,
过点 作 于点 , 为 的中点,用向量的方法证明:
(1) ;
(2) 三点共线.