文档内容
河池市 2024 年春季学期高一期末学业水平质量检测
数学
全卷满分150分,考试时间120分钟.
注意事项:
1.答题前,先将自己的姓名、准考证号填写在试卷和答题卡上,并将条形码粘贴在答题卡上
的指定位置.
2.请按题号顺序在答题卡上各题目的答题区域内作答,写在试卷,草稿纸和答题卡上的非答
题区域均无效.
3.选择题用2B铅笔在答题卡上把所选答案的标号涂黑;非选择题用黑色签字笔在答题卡上
作答;字体工整,笔迹清楚.
4.考试结来后,请将答题卡上交.
5.本卷主要考查内容:必修第二册.
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是
符合题目要求的.
1. 某市市场监管局为了了解饮料的质量,从该市区某超市在售的 种饮料中抽取了 种饮料,对其质量
进行了检查.在这个问题中, 是( )
.
A 总体 B. 个体 C. 样本 D. 样本量
2. 矩形的直观图是( )
A. 正方形 B. 矩形 C. 三角形 D. 平行四边形
3. 下列说法中正确的是( )
的
A. 随机事件发生 频率就是这个随机事件发生的概率
B. 在 次随机试验中,一个随机事件 发生的频率具有确定性
C. 随着试验次数 的增大,一个随机事件 发生的频率会逐渐稳定于事件 发生的概率
D. 在同一次试验中,每个试验结果出现的频率之和不一定等于1
4. 已知圆锥的侧面展开图是半径为 ,圆心角为 的扇形,则该圆锥的体积为( )
第1页/共8页
学科网(北京)股份有限公司A. B. C. D.
5. 国家队射击运动员小王在某次训练中10次射击成绩(单位:环)如下:6,5,9,6,4,8,9,8,7,
5,则这组数据的第60百分位数为( )
A. 6.5 B. 7 C. 7.5 D. 8
6. 欧拉恒等式 ( 为虚数单位, 为自然对数的底数)被称为数学中最奇妙的公式.它是复分析
中欧拉公式 的特例:当自变量 时, ,得 .根据
欧拉公式,复数 在复平面上所对应的点在( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
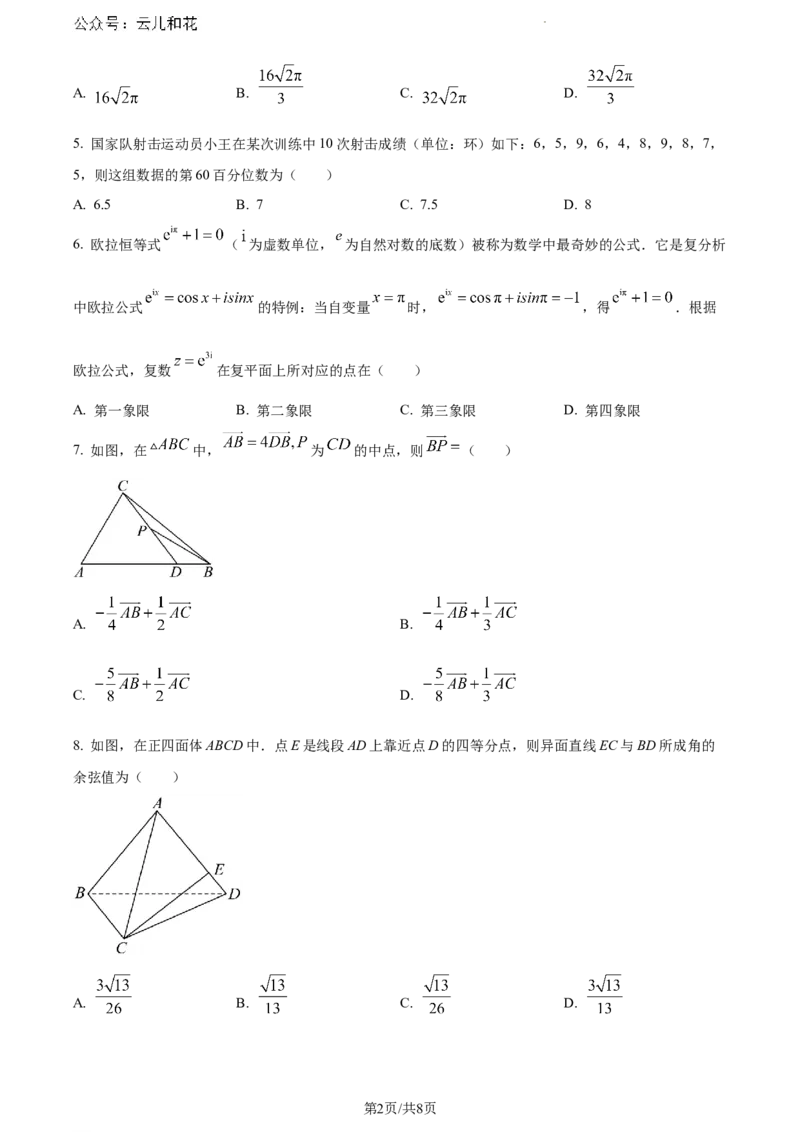
7. 如图,在 中, 为 的中点,则 ( )
A. B.
C. D.
8. 如图,在正四面体ABCD中.点E是线段AD上靠近点D的四等分点,则异面直线EC与BD所成角的
余弦值为( )
A. B. C. D.
第2页/共8页
学科网(北京)股份有限公司二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目
要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.
的
9. 已知复数 ,则下列说法正确 是( )
A. 若 是实数,则 与 的虚部互为相反数
B. 若 且 ,则 在复平面内对应的点关于实轴对称
C. 若 ,则
D. 若 ,则
10. 已知 , 是两条不同的直线, , , 是三个不同的平面,则下列说法正确的是( )
.
A 若 , ,则 B. 若 , , ,则
C. 若 , ,则 D. 若 , , ,则
11. 口袋中装有大小质地完全相同的白球和黑球各2个,从中不放回的依次取出2个球,事件 “取出的
两球同色”,事件 “第一次取出的是白球”.事件 “第二次取出的是白球”,事件 “取出的两球
不同色”,则( )
A. B. A与B相互独立
.
C A与C相互独立 D.
三、填空题:本题共3小题,每小题5分,共15分.
12. 已知向量 与 的夹角为 , .则 ___________.
13. 已知射击运动员甲击中靶心的概率为0.72,射击运动员乙击中靶心的概率为0.85,且甲、乙两人是否
击中靶心互不影响.若甲、乙各射击一次,则至少有一人击中靶心的概率为___________.
14. 某工厂需要制作一个如图所示的模型,该模型为长方体 挖去一个四棱锥
第3页/共8页
学科网(北京)股份有限公司后所得的几何体,其中 为长方体 的中心, , , , 分别为所在棱的中点,
, ,那么该模型的表面积为___________.
四、解答题:本题共5小题,共77分,解答应写出必要的文字说明、证明过程及演算步骤.
15. 已知 的内角 的对边分别为 .
(1)求 ;
(2)若 ,请判断 是锐角三角形,直角三角形还是钝角三角形?
16. 团建的目的是增强团队凝聚力和团队融合度,提高团队间熟悉感和协助能力,在紧张的工作中放松,
能够更好地完成日常工作.某文化传媒公司团建活动是投篮比赛,其中10名员工的投中个数(每人投10
个球)统计表如下:
编号 1 2 3 4 5 6 7 8 9 10
投中个数 7 9 8 9 8 10 7 7 6 9
(1)求这10名员工在本次投篮比赛中投中个数的平均数和方差;
(2)从投进9个球和10个球的员工中选2人分享活动感受,求这2人恰好都是投进9个球的员工的概率.
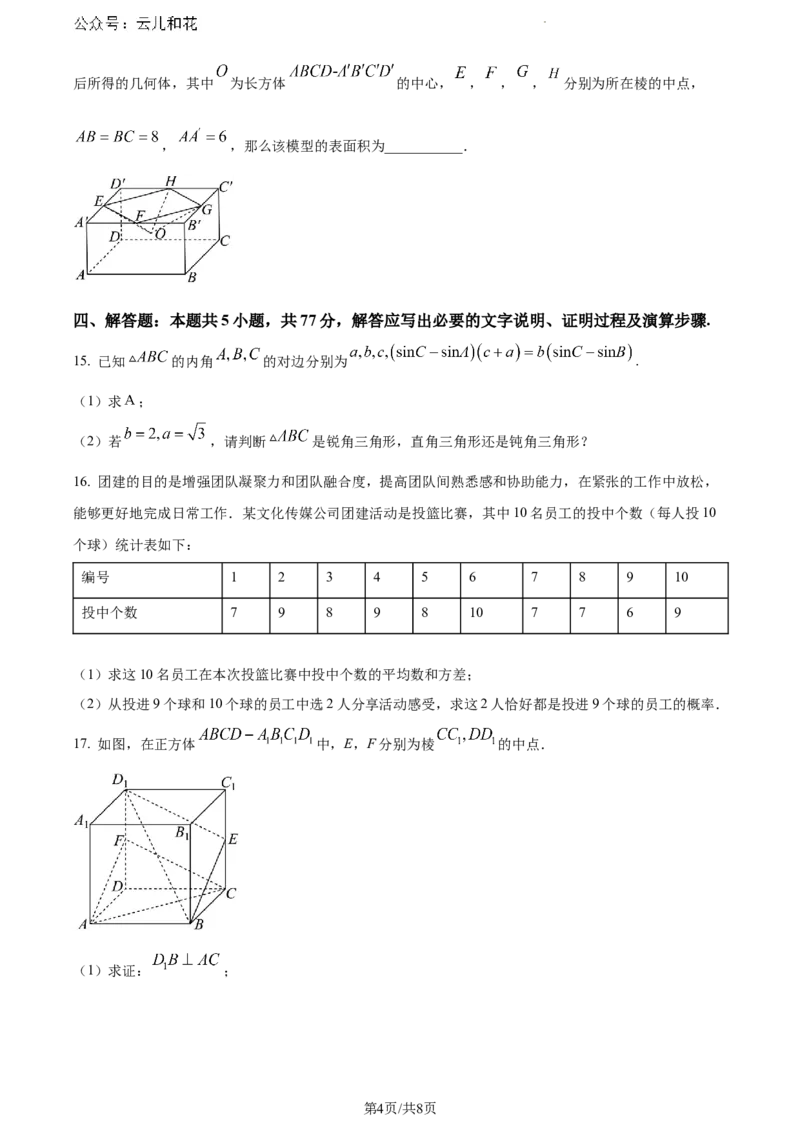
17. 如图,在正方体 中,E,F分别为棱 的中点.
(1)求证: ;
第4页/共8页
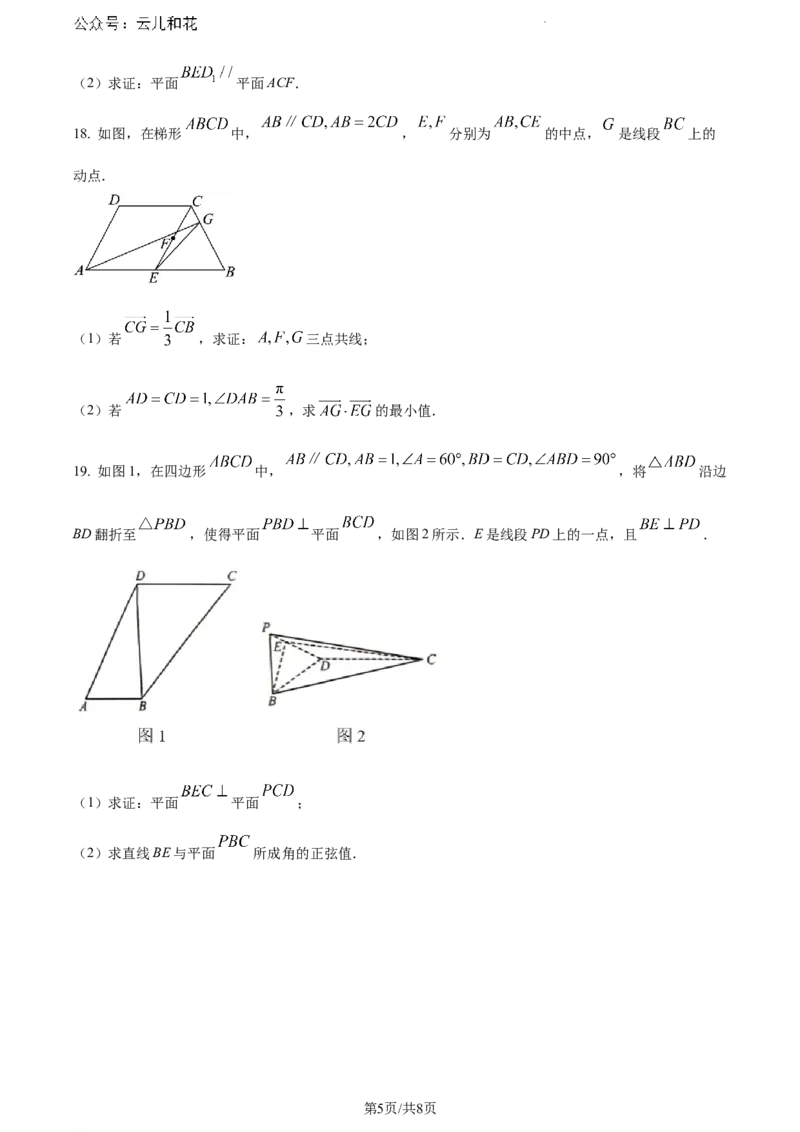
学科网(北京)股份有限公司(2)求证:平面 平面ACF.
18. 如图,在梯形 中, , 分别为 的中点, 是线段 上的
动点.
(1)若 ,求证: 三点共线;
(2)若 ,求 的最小值.
19. 如图1,在四边形 中, ,将 沿边
BD翻折至 ,使得平面 平面 ,如图2所示.E是线段PD上的一点,且 .
(1)求证:平面 平面 ;
(2)求直线BE与平面 所成角的正弦值.
第5页/共8页
学科网(北京)股份有限公司河池市 2024 年春季学期高一期末学业水平质量检测
数学
全卷满分150分,考试时间120分钟.
注意事项:
1.答题前,先将自己的姓名、准考证号填写在试卷和答题卡上,并将条形码粘贴在答题卡上
的指定位置.
2.请按题号顺序在答题卡上各题目的答题区域内作答,写在试卷,草稿纸和答题卡上的非答
题区域均无效.
3.选择题用2B铅笔在答题卡上把所选答案的标号涂黑;非选择题用黑色签字笔在答题卡上
作答;字体工整,笔迹清楚.
4.考试结来后,请将答题卡上交.
5.本卷主要考查内容:必修第二册.
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是
符合题目要求的.
【1题答案】
【答案】D
【2题答案】
【答案】D
【3题答案】
【答案】C
【4题答案】
【答案】B
【5题答案】
【答案】C
【6题答案】
【答案】B
【7题答案】
【答案】C
【8题答案】
【答案】A
第6页/共8页
学科网(北京)股份有限公司二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目
要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.
【9题答案】
【答案】AB
【10题答案】
【答案】BC
【11题答案】
【答案】BCD
三、填空题:本题共3小题,每小题5分,共15分.
【12题答案】
【答案】
【13题答案】
【答案】 ##
【14题答案】
【答案】
四、解答题:本题共5小题,共77分,解答应写出必要的文字说明、证明过程及演算步骤.
【15题答案】
【答案】(1)
(2) 是直角三角形
【16题答案】
【答案】(1)平均数8,方差1.4;
(2) .
【17题答案】
【答案】(1)证明见解析;
(2)证明见解析.
【18题答案】
【答案】(1)证明见解析;
第7页/共8页
学科网(北京)股份有限公司(2) .
【19题答案】
【答案】(1)证明见解析;
(2) .
第8页/共8页
学科网(北京)股份有限公司