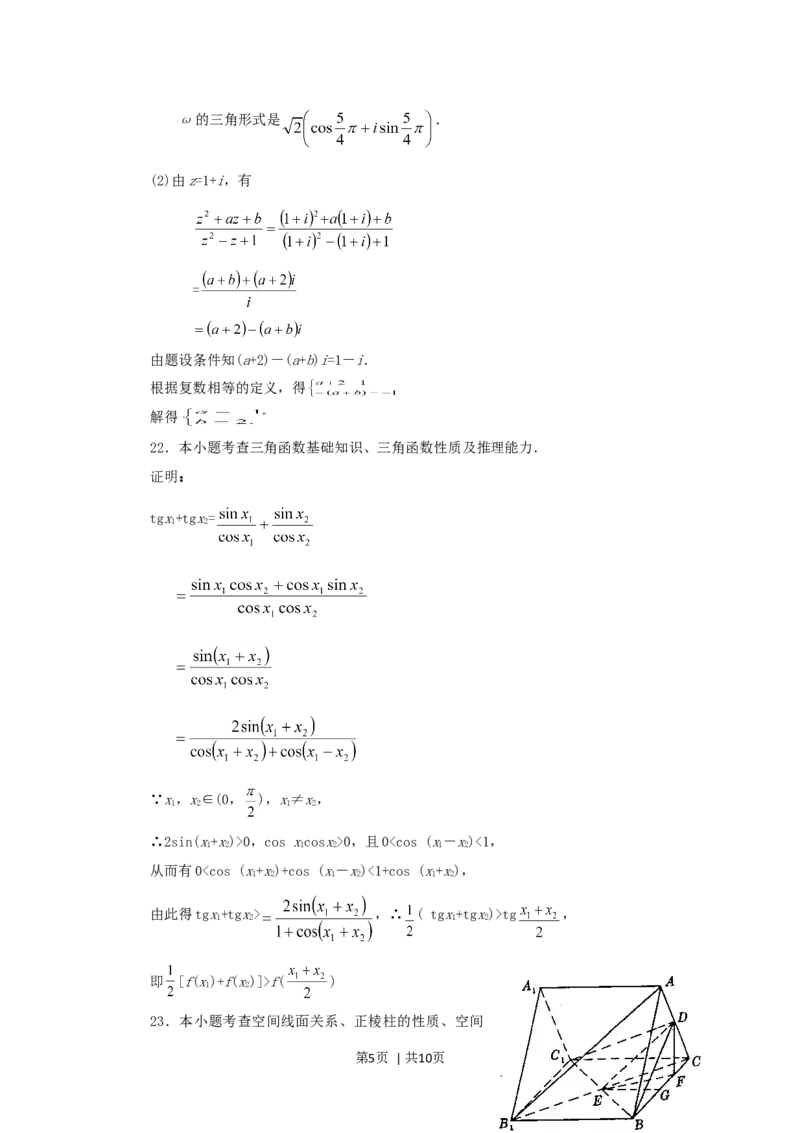文档内容
1994 年江苏高考理科数学真题及答案
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.共150分,考试时间120分钟.
第Ⅰ卷(选择题共65分)
一、选择题:本大题共15小题;第(1)—(10)题每小题4分,第(11)—(15)题每小题5
分,共65分,在每小题给出的四个选项中,只有一项是符合题目要求的
王新奎新疆屯敞
(1) 设全集I={0,1,2,3,4},集合A={0,1,2,3},集合B={2,3,4},则
( )
(A) {0} (B) {0,1}
(C) {0,1,4} (D) {0,1,2,3,4}
(2) 如果方程x2+ky2=2表示焦点在y轴上的椭圆,那么实数k的取值范围是 ( )
(A) (0,+∞) (B) (0,2) (C) (1,+∞) (D) (0,1)
(3) 极坐标方程 所表示的曲线是 ( )
(A) 双曲线 (B) 椭圆 (C) 抛物线 (D) 圆
(4) 设θ是第二象限的角,则必有 ( )
(A) (B)
(C) (D)
(5) 某种细菌在培养过程中,每 20分钟分裂一次(一个分裂为两个).经过3小时,
这种细菌由1个可繁殖成 ( )
(A) 511个 (B) 512个 (C) 1023个 (D) 1024个
(6) 在下列函数中,以 为周期的函数是 ( )
(A) y=sin2x+cos4x (B) y=sin2xcos4x
(C) y=sin2x+cos2x (D) y=sin2xcos2x
(7) 已知正六棱台的上、下底面边长分别为2和4,高为2,则其体积为 ( )
(A) 32 (B) 28 (C) 24 (D) 20
(8) 设F和F为双曲线 -y2=1的两个焦点,点P在双曲线上且满足∠FPF=90°,
1 2 1 2
则△FPF的面积是 ( )
1 2
第1页 | 共10页(A) 1 (B) (C) 2 (D)
(9) 如果复数z满足│z+i│+│z-i│=2,那么│z+i+1│的最小值是 ( )
(A) 1 (B) (C) 2 (D)
(10) 有甲、乙、丙三项任务,甲需2人承担,乙、丙各需1人承担.从10人中选派
4人承担这三项任务,不同的选法共有 ( )
(A) 1260种 (B) 2025种 (C) 2520种 (D) 5040种
(11) 对于直线m、n和平面α、β,α⊥β的一个充分条件是 ( )
(A) m⊥n,m∥α,n∥β (B) m⊥n,α∩β=m,n α
(C) m∥n,n⊥β,m α (D) m∥n,m⊥α,n⊥β
(12) 设函数f(x)=1- (-1≤x≤0),则函数y=f-1(x)的图像是 ( )
(13) 已知过球面上 A、B、C三点的截面和球心的距离等于球半径的一半,且
AB=BC=CA=2,则球面面积是 ( )
(A) π (B) π (C) 4π (D) π
(14) 函数y=arccos(sinx) 的值域是 ( )
(A) (B) (C) (D)
(15) 定义在(-∞,+∞)上的任意函数f(x)都可以表示成一个奇函数g(x)和一个偶
函数h(x)之和,如果f(x)=lg(10x+1),x∈(-∞,+∞),那么 ( )
(A) g(x)=x,h(x)=lg(10x+10-x+2)
(B) g(x)= [lg(10x+1)+x],h(x)= [lg(10x+1)-x]
(C) g(x)= ,h(x)=lg(10x+1)-
(D) g(x)=- ,h(x)=lg(10x+1)+
第2页 | 共10页第Ⅱ卷(非选择题共85分)
二、填空题 (本大题共5小题,共6个空格;每空格4分,共24分.把答案填在题中横
线上)
(16) 在(3-x)7的展开式中,x5的系数是 (用数字作答)
王新奎新疆屯敞
(17) 抛物线y2=8-4x的准线方程是 ,圆心在该抛物线的顶点且与其
准线相切的圆的方程是
王新奎新疆屯敞
(18) 已知sinθ +cosθ = ,θ∈(0,π),则ctgθ的值是_____________
王新奎新疆屯敞
(19) 设圆锥底面圆周上两点A、B间的距离为2,圆锥顶点到直线AB的距离为 ,
AB和圆锥的轴的距离为1,则该圆锥的体积为_________
王新奎新疆屯敞
(20) 在测量某物理量的过程中,因仪器和观察的误差,使得n次测量分别得到a,
1
a,…a,共n个数据,我们规定所测量物理量的“最佳近似值” a是这样一个量:与其
2 n
他近似值比较,a与各数据的差的平方和最小.依此规定,从a,a,…,a推出的
1 2 n
a=_________
王新奎新疆屯敞
三、解答题(本大题共5小题,共61分;解答应写出文字说明、证明过程或推演步骤)
(21) (本小题满分11分)
已知z=1+i.
(1)设ω=z2+3 -4,求ω的三角形式;
(2)如果 ,求实数a,b的值.
(22) (本小题满分12分)
已知函数 f(x)=tgx,x∈(0, ).若 x,x∈(0, ),且 x≠x,证明
1 2 1 2
[f(x)+f(x)]>f( )
1 2
(23) (本小题满分12分)
如图,已知ABC-ABC是正三棱柱,D是AC中点.
1 1 1
(1)证明AB∥平面DBC;
1 1
(2)假设AB⊥BC,求以BC为棱,DBC与CBC为面的二
1 1 1 1 1
第3页 | 共10页面角α的度数.
(24) (本小题满分12分)
已知直线l过坐标原点,抛物线C顶点在原点,焦点在x轴
正半轴上.若点 和点B(0,8)关于l的对称点都在C上,
求直线l和抛物线C的方程.
(25) (本小题满分14分)
设{a}是正数组成的数列,其前n项和为S,并且对于所有
n n
的自然数n,a与2的等差中项等于S与2的等比中项.
n n
(1)写出数列{a}的前3项;
n
(2)求数列{a}的通项公式(写出推证过程);
n
(3)令 ,求
参考答案
一、选择题(本题考查基本知识和基本运算)
1.C 2.D 3.D 4.A 5.B 6.D 7.B 8.A 9.A
10.C 11.C 12.B 13.D 14.B 15.C
二、填空题(本题考查基本知识和基本运算)
16.-189 17.x=3,(x-2)2+y2=1 18. 19.
20.
三、解答题
21.本小题考查共轭复数、复数的三角形式等基础知识及运算能力.
解:(1)由z=1+i,有
ω=z2+3 -4
=(1+i)2+3 -4
=2i+3(1-i)-4=-1-i,
第4页 | 共10页ω的三角形式是 .
(2)由z=1+i,有
=
由题设条件知(a+2)-(a+b)i=1-i.
根据复数相等的定义,得
解得
22.本小题考查三角函数基础知识、三角函数性质及推理能力.
证明:
tgx+tgx=
1 2
∵x,x∈(0, ),x≠x,
1 2 1 2
∴2sin(x+x)>0,cos xcosx>0,且0 ,∴ ( tgx+tgx)>tg ,
1 2 1 2
即 [f(x)+f(x)]>f( )
1 2
23.本小题考查空间线面关系、正棱柱的性质、空间
第5页 | 共10页想象能力和逻辑推理能力.
(1)证明:
∵ABC-ABC是正三棱柱,∴四边形BBCC是矩形.
1 1 1 1 1
连结BC交BC于E,则BE=EC.连结DE.
1 1 1
在△ABC中,∵AD=DC,∴DE∥AB.
1 1
又AB 平面DBC,DE 平面DBC,∴AB∥平面DBC.
1 1 1 1 1
(2)解:作DF⊥BC,垂足为F,则DF⊥面BBCC,连结EF,则EF是ED在平面BBCC上
1 1 1 1
的射影.
∵AB⊥BC,
1 1
由(1)知AB∥DE,∴DE⊥BC,则BC⊥EF,∴∠DEF是二面角α的平面角.
1 1 1
设AC=1,则DC= .∵△ABC是正三角形,∴在Rt△DCF中,
DF=DC·sinC= ,CF=DC·cosC= .取BC中点G.∵EB=EC,∴EG⊥BC.
在Rt△BEF中,
EF2=BF·GF,又BF=BC-FC= ,GF= ,
∴EF2= · ,即EF= .∴tg∠DEF= .∴∠DEF=45°.
故二面角α为45°.
24.本小题考查直线与抛物线的基本概念和性质,解析几何的基本思想方法以及综合
运用知识解决问题的能力.
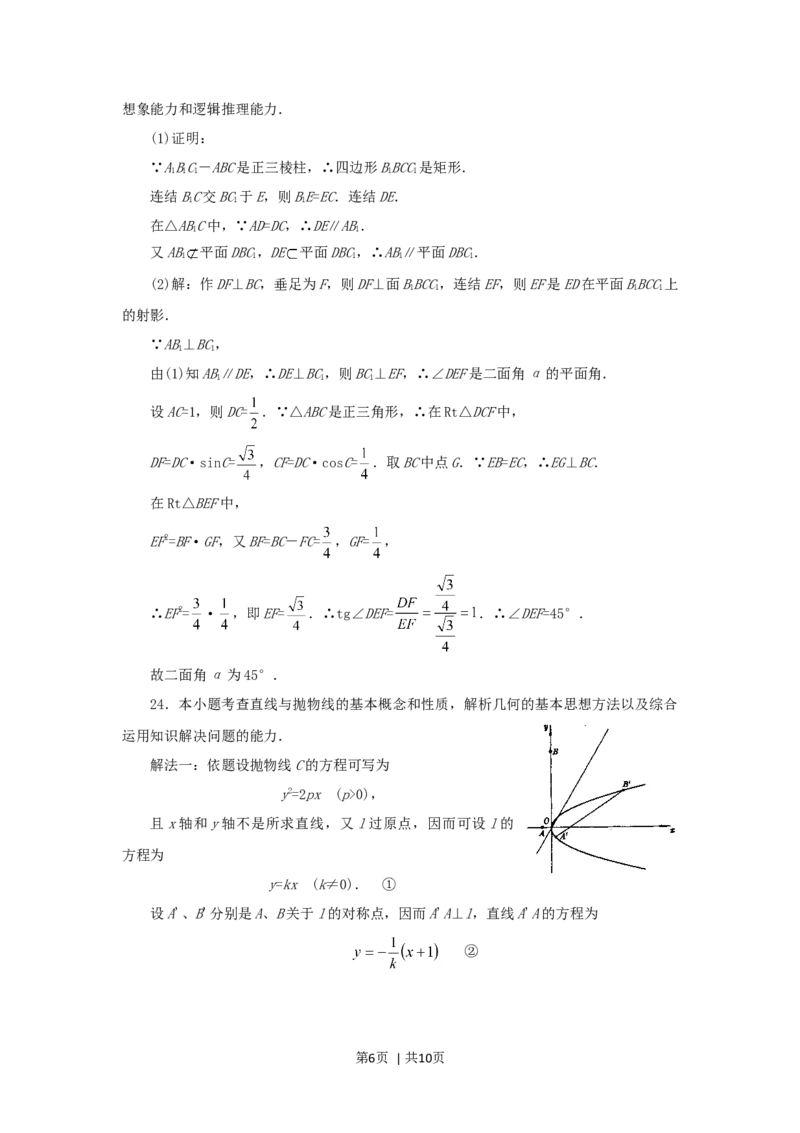
解法一:依题设抛物线C的方程可写为
y2=2px (p>0),
且x轴和y轴不是所求直线,又l过原点,因而可设l的
方程为
y=kx (k≠0). ①
设A'、B'分别是A、B关于l的对称点,因而A'A⊥l,直线A'A的方程为
②
第6页 | 共10页由①、②联立解得AA'与l的交点M的坐标为 .
又M为AA'的中点,从而点A'的坐标为
x = ,
A'
y = . ③
A'
同理得点B'的坐标为
x = , y = . ④
B' B'
又A'、B'均在抛物线y2=2px(p>0)上,由③得
,由此知k≠±1,
即 ⑤
同理由④得 .
即 .
从而 = ,
整理得 k2-k-1=0.
解得
但当 时,由③知 ,
这与A'在抛物线y2=2px(p>0)上矛盾,故舍去 .
第7页 | 共10页设 ,则直线l的方程为 .
将 代入⑤,求得 .
所以直线方程为
.
抛物线方程为
.
解法二:设点A、B关于l的对称点分别为A'(x、y)、B'(x,y),则
1 1 2 2
|OA'|=|OA|=1,|OB'|=|OB|=8.
设由x轴正向到OB'的转角为α,则
x=8cosα,y=8sinα. ①
2 2
因为A'、B'为A、B关于直线l的对称点,而∠BOA为直角,故∠B'OA'为直角,因此
x=cos =sinα,y=sin =-cosα, ②
1 1
由题意知x>0,x>0,故α为第一象限角.
1 2
因为A'、B'都在抛物线y2=2px上,将①、②代入得
cos2α=2p·sinα,64sin2α=2p·8cosα.
∴8sin3α=cos3α,
∴2sinα=cosα,
解得 .
将 代入cos2α=2psinα得
,
∴抛物线C的方程为 .
因为直线l平分∠B'OB,故l的斜率
第8页 | 共10页∴直线l的方程为 .
25.本小题考查等差数列、等比数列、数列极限等基础知识考查逻辑推理能力和分析
问题与解决问题的能力.
解:(1)由题意,当n=1时有 ,S=a,
1 1
∴ ,
解得 a=2.
1
当n=2时有 ,S=a+ a,a=2代入,整理得
2 1 2 1
(a-2)2=16.
2
由a>0,解得 a=6.
2 2
当n=3时有 ,S=a+ a+ a,将a=2,a=6代入,整理得
3 1 2 3 1 2
(a-2)2=64.
3
由a>0,解得 a=10.
3 3
故该数列的前3项为2,6,10.
(2)解法一:由(1)猜想数列{a}有通项公式a =4n-2.
n n
下面用数学归纳法证明数列{ a }的通项公式是
n
a =4n-2 (n∈N).
n
①当n=1时,因为4×1-2=2,又在(1)中已求出a=2,所以上述结论成立.
1
②假设n=k时结论成立,即有a=4k-2.由题意,有
k
,
将a=4k-2代入上式,得2k= ,解得S=2k2.
k k
由题意,有 ,S =S+a ,
k+1 k k+1
第9页 | 共10页将S=2k2代入,得 =2(a +2k2),整理得 -4 a +4-16 k2=0.
k k+1 k+1
由a >0,解得a =2+4k.所以a =2+4k=4(k+1)-2.
k+1 k+1 k+1
这就是说,当n=k+1时,上述结论成立.
根据①、②,上述结论对所有的自然数n成立.
解法二:由题意,有 ,整理得S= (a+2)2,
n n
由此得 S = (a +2)2,
n+1 n+1
∴a = S -S = [(a +2)2-(a+2)2],
n+1 n+1 n n+1 n
整理得(a + a)( a -a-4)=0,
n+1 n n+1 n
由题意知 a +a≠0,∴a -a=4.
n+1 n n+1 n
即数列{ a }为等差数列,其中a=2,公差d=4.∴a =a+(n-1)d=2+4(n-1),
n 1 n 1
即通项公式为a =4n-2.
n
(3)解:令c=b-1,则
n n
,
b+b+…+b-n=c+c+…+c
1 2 n 1 2 n
=
.
∴
第10页 | 共10页