文档内容
2024—2025 学年度第二学期期中考试高一年级数学试题
卷面满分:150 分 考试时间:120 分钟
一、选择题:本题共 8 小题,每小题 5 分,共 40 分.在每小题给出的四个选项中,只有一
项 是符合题目要求的.
1. 等于 ( )
A. B. C. D.
2.若复数 满足 ( 为虚数单位),则 的虚部为 ( )
A.−3+i B.i C.−3 D.1
3.在△ABC中,角 的对边分别是 ,若 ,则 ( )
A. B.2 C.3 D.
4.下列说法正确的是 ( )
A.三点确定一个平面
B.和两条异面直线都相交的两条直线必定是异面直线
C.水平放置的矩形的直观图是平行四边形
D.以直角三角形的一边为轴旋转一周所得的旋转体是圆锥
5.已知 , ,则 ( )
A. B. C. D.
B a−c
6.在△ABC中,角A、B、C所对边分别为a、b、c.若2sin2
= ,则该三角形一定是(
2 a
)
A.正三角形 B.直角三角形 C.等腰直角三角形 D.等腰三角形
1 √3 2tan12° √1−cos50°
7.设a= cos7°− sin7°,b= ,c= ,则有 ( )
2 2 1+tan212° 2
A. B. C. D.8.如图,“六芒星”是由两个边长为6正三角形组成,中心重合于点 且三组对边分别平行,点 , 是
“六芒星”(如图)的两个顶点,动点 在“六芒星”上(内部以及边界),则 的取值范围是
( )
A.[−8,8] B.[−6,6]
C.
[−6√3,6√3]
D.
[−4,4√3]
二、多项选择题:本题共 3 小题,毎小题 6 分,共 18 分.在每小题给出的四个选项中,有
多 项符合题目要求.全部选对的得 6 分,部分选对的得部分,有选错的得 0 分.
9.已知非零复数 ,其共轭复数分别为 ,则下列选项正确的是 (
)
z +z ∈R z =|z |2 z +z =z +z |z ⋅z |=|z ||z |
A. 1 1 B. 2 2 2 C. 1 2 1 2 D. 1 2 1 2
10.已知 , 与 夹角为 ,若 且 ( , ),则
下 列 说 法 正 确 的 是
( )
A.当 时, 在 上的投影向量为 B.当 时,
1 √13−1
x= y=
C.当 2时, 4 D. 的最大值为0
11.在锐角△ABC中,角 所对边分别为 ,且 .则下列说法正确的是
( )
( π)
0,
A. A=2B B.角B的范围是 4
3 1 1 4
sinB= + =
C.若∠BAC 的平分线交 BC 于D,AD=2, 5,则b c 5 ;
(√2 2√3)
c
,
2 3
D.a 的取值范围是
三、填空题:本题共 3 个小题,每小题 5 分,满分 15 分.
⃗AB=(1,2) ⃗BC=(3,m) ⃗AD=(−1,2m)
12.已知向量 , , ,若A,C,D三点共线,则 .
π 1 7√2
α∈(0, ),β∈(0,π) tan(α−β)= ,cosβ=−
13.已知 2 ,且 2 10 ,
(1)
tanα=_________
; (2)
2α−β
=________________.
14.如图,在四边形
ABCD 中,∠ABC=120°,∠CAD=30°,BC⊥CD
,S
1 =_____
DC=2√3BC ΔABC,ΔACD S ,S S
, 的面积分别为 1 2,则 2 .四、解答题:共 5 个小题,满分 77 分,解答应写出文字说明、证明过程或演算步
骤.
15.(本小题满分 13 分)
(1)已知 ,若 为纯虚数,求m的值.
(2)设复数 , .若 是实数,求 ;
(3)已知复数z满足 ,求z.
16 .(本小题满分 15 分)
已知三棱锥 满足 .
(1)证明:直线 与直线 是异面直线;
(2)若 为 的中点, 为 的中点,求异面直线 与 所成角的余弦值.
V
E C
A F
B
17 .(本小题满分 15 分)
在直角梯形 中, , , ,点 是 边上的中点.
(1)若点 满足 ,且 ,求
6λ+μ
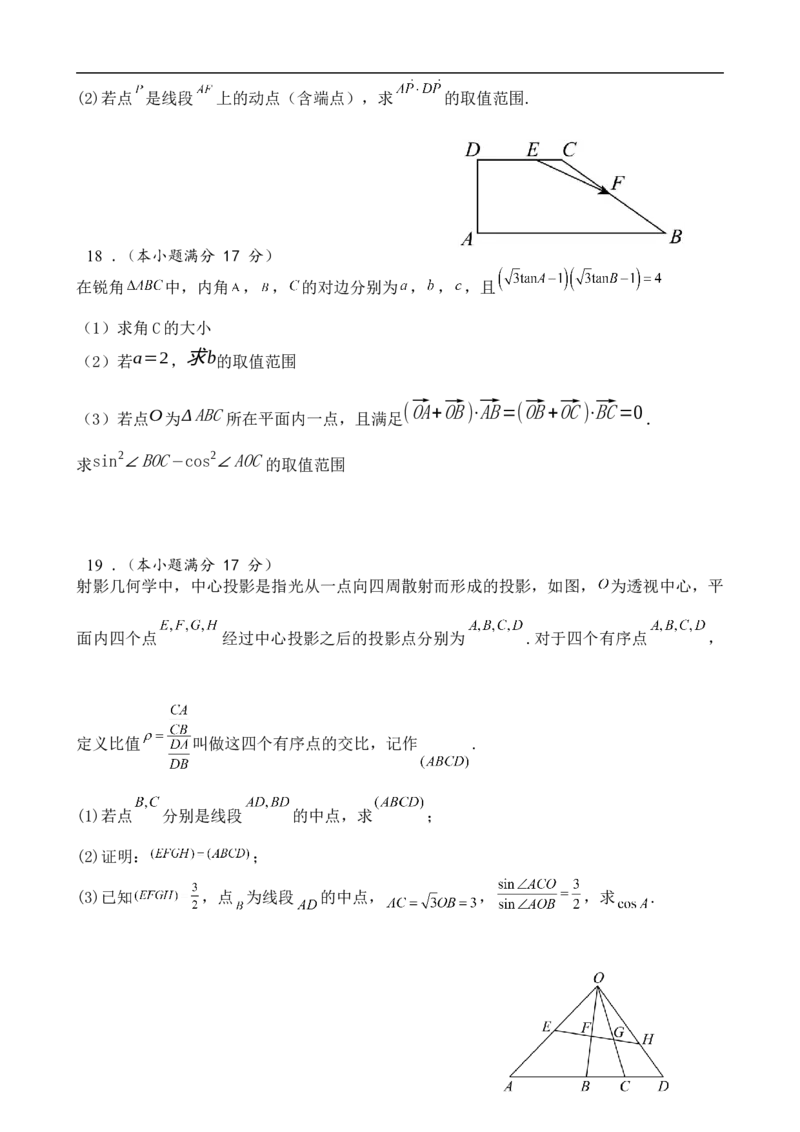
的值;(2)若点 是线段 上的动点(含端点),求 的取值范围.
18 .(本小题满分 17 分)
在锐角 中,内角 , , 的对边分别为 , , ,且
(1)求角C的大小
(2)若a=2, 求b 的取值范围
(3)若点O为ΔABC
所在平面内一点,且满足
(O⃗A+O⃗B)⋅ ⃗AB=(O⃗B+O⃗C)⋅ ⃗BC=0
.
求
sin2 ∠BOC−cos2 ∠AOC
的取值范围
19 .(本小题满分 17 分)
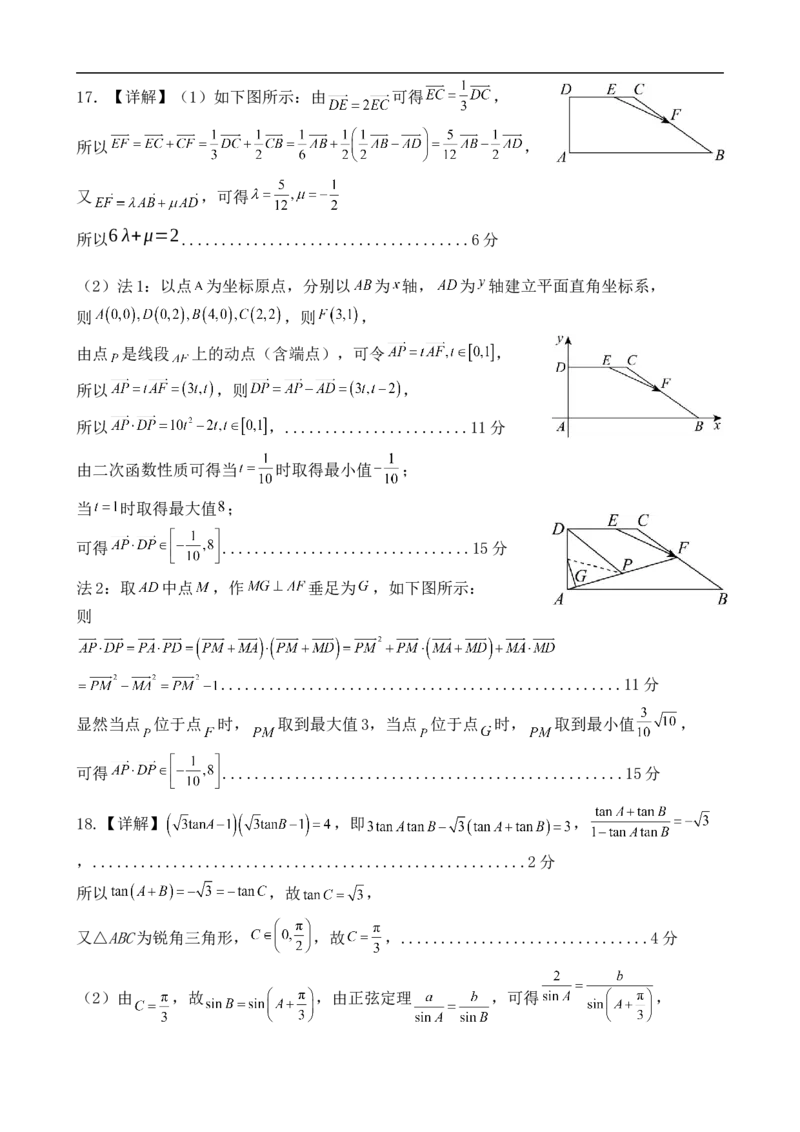
射影几何学中,中心投影是指光从一点向四周散射而形成的投影,如图, 为透视中心,平
面内四个点 经过中心投影之后的投影点分别为 .对于四个有序点 ,
定义比值 叫做这四个有序点的交比,记作 .
(1)若点 分别是线段 的中点,求 ;
(2)证明: ;
(3)已知 ,点 为线段 的中点, , ,求 .数学试题答案
一、选择题:本题共8小题,每小题5分,共40分.
1.A 2.D 3.B 4.C 5.D 6.B 7.D 8.B
二、选择题:本题共3小题,每小题6分,共18分.
9.ACD 10.BCD 11.ACD
三、填空题:本题共3小题,每小题5分,共15分.
2 1 3 √5
− − π
9 3 4 6
12. 13. (1) (2) 14.
四、解答题:本大题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.
15.【详解】(1)因为 为纯虚数,
所以 且 ,解得 ;............................................4分
(2) , 是实数, ,即 ,
..............................................................8分
(3)因为 ,且 ,因此可设 ,
则 ,
由题意可得 ,所以 ,
解得 ,即 .........................................................13分
16.【详解】(1)因为直线 平面 ,点 平面 ,点 ,点 平面 ,
所以直线 与直线 是异面直线...............................................6分
(2)如图:取 的中点 ,连接 , , ,.......8分
所以 , ,所以异面直线 与 所成角为 (或其补角),.......10分
因为 ,所以 , ,在 中, ,
, ,所以有 ,
由余弦定 ,..............13分
π
(0, ]
2
因为异面直线所成角范围为
13
32
所以异面直线 与 所成角的余弦值为 ..............15分17.【详解】(1)如下图所示:由 可得 ,
所以 ,
又 ,可得
所以
6λ+μ=2
....................................6分
(2)法1:以点 为坐标原点,分别以 为 轴, 为 轴建立平面直角坐标系,
则 ,则 ,
由点 是线段 上的动点(含端点),可令 ,
所以 ,则 ,
所以 ,.......................11分
由二次函数性质可得当 时取得最小值 ;
当 时取得最大值 ;
可得 ...............................15分
法2:取 中点 ,作 垂足为 ,如下图所示:
则
..................................................11分
显然当点 位于点 时, 取到最大值3,当点 位于点 时, 取到最小值 ,
可得 ..................................................15分
18.【详解】 ,即 ,
,......................................................2分
所以 ,故 ,
又△ABC为锐角三角形, ,故 ,...............................4分
(2)由 ,故 ,由正弦定理 ,可得 ,故可得
由△ABC为锐角三角形可得: ,解得 ,故 ,
则 ,则 ................................................10分
(3)由题意知O为△ABC的外心,所以∠BOC=2A,∠AOC=2B
1−cos4 A 1+cos4B
sin2 ∠BOC−cos2 ∠AOC=sin22A−cos22B=
−
2 2
........12分
1 1 1
=− (cos4 A+cos4B)=− [cos(480°−4B)+cos4B]=− [cos(120°−4B)+cos4B]
2 2 2
1 1 √3 1 √3 1
− (− cos4B+ sin4B+cos4B)=− ( sin4B+ cos4B)
2 2 2 2 2 2
1 π
=− sin(4B+ )
2 6
......................................................15分
π π π 5π 13π 1 π 1 1
B∈( , ) 4B+ ∈( , ),∴− sin(4B+ )∈(− , ]
由第二问知 6 2 所以 6 6 6 2 6 4 2
1 1
(− , ]
sin2 ∠BOC−cos2 ∠AOC 4 2 ,.........................17分
所以 的取值范围
19.【详解】(1)由已知 , ,所以 ...................4分
(2)在 , , , 中,
,同理 ,
所以 ,..............................6分又在 , , , 中, ,
同理 ,所以 ,.........8分
又 , , , ,
所以 ,所以 .............10分
(EFGH)=(ABCD)
(3)方法一:由 ,可得 ,即 ,所以 ,
又点B为线段AD的中点,即 ,所以 ,
又 ,所以 , , ,由已知 ,所以 .
设 , ,由 ,得 ,
即 ,解得 ,…①.......................12分
在三角形AOB中,由正弦定理可得 ,得 ,…②
在 中,由正弦定理可得 ,得 ,…③
又 ,
得 ,即 ,…④...................14分
由①④解得 , (负值舍去),即 , ,
所以 ..................................17分
方法二:因为 ,所以 ,设 ,则 ,
又B为线段AD的中点,所以 ,
又已知 , ,所以 ,
所以 ,得 ,所以 , ,............12分
由 ,得 ,所以 ,设 ,则 ,......................................14分
由 , 互补得 ,即 ,
解得 ,所以 , ,所以 .....17分