文档内容
格致课堂
8.3.1 棱柱、棱锥、棱台的表面积和体积
一、选择题
1.若底面是菱形的棱柱其侧棱垂直于底面,且侧棱长为5,它的对角线的长分别是9和15,则这个棱柱的
侧面积是( ).
A.130 B.140 C.150 D.160
【答案】D
【解析】
设直四棱柱 中,对角线 ,
因为 平面 ,平面 ,所以 ,
在 中, ,可得 ,
同理可得 ,
因为四边形 为菱形,可得 互相垂直平分,
所以 ,即菱形 的边长为 ,
因此,这个棱柱的侧面积为 ,
故选D.
2.若正方体的棱长为 ,则以该正方体各个面的中心为顶点的凸多面体的体积为 ( )
A. B. C. D.
【答案】B
【解析】解:所求八面体体积是两个底面边长为1,高为 , 的四棱锥的体积和,一个四棱锥体积V=
1格致课堂
,故八面体体积V=2V= ,故选B.
1
3.长方体的过一个顶点的三条棱长的比是1:2:3,对角线长为 ,则这个长方体的体积为( )
A.6 B.12 C.24 D.48
【答案】D
【解析】∵长方体的过一个顶点的三条棱长的比是1:2:3,
∴设三条棱长分别为k,2k,3k
则长方体的对角线长为 =k =2
∴k=2
长方体的长宽高为6,4,2
∴这个长方体的体积为6×4×2=48
故答案为48应选D
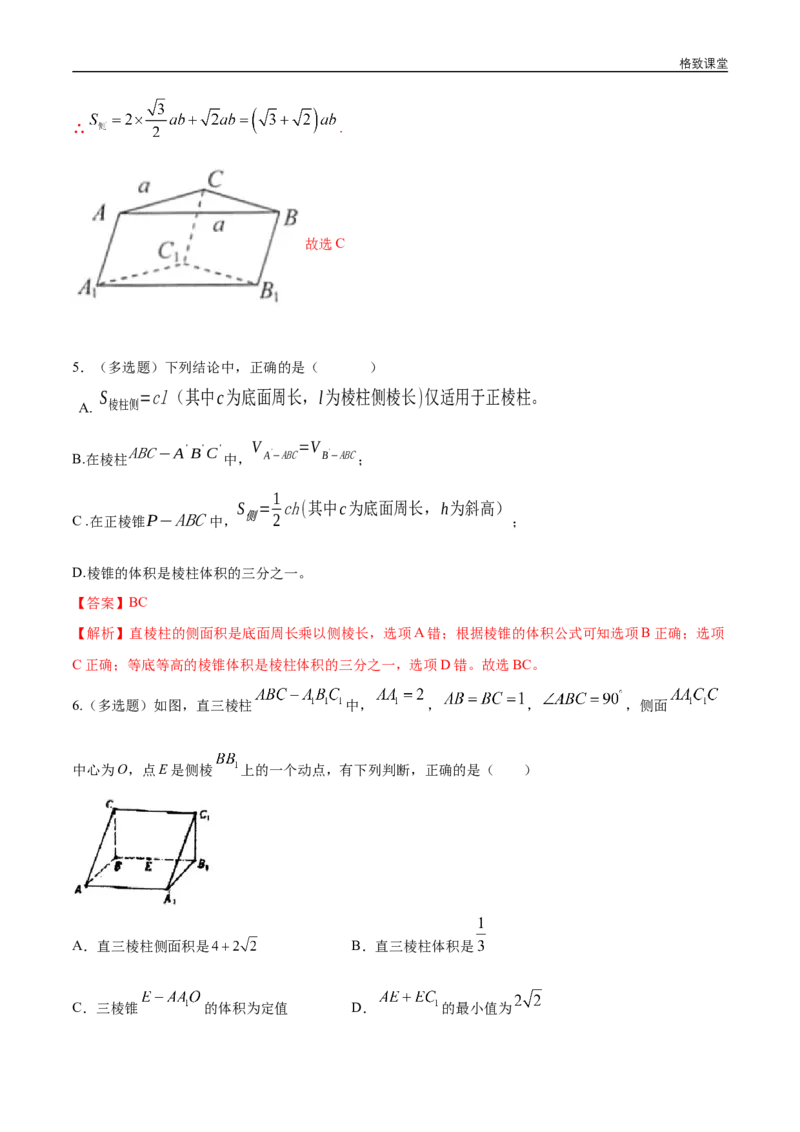
4.三棱柱 中, , , , ,
侧棱长为 ,则其侧面积为( )
A. B. C. D.
【答案】C
【解析】如图,由已知条件可知,侧面 和侧面 为一般的平行四边形,侧面 为矩形.
在 中, , ,
∴ ,∴ .
∵ , ,
∴点 到直线 的距离为 .
∴ .格致课堂
∴ .
故选C
5.(多选题)下列结论中,正确的是( )
S =cl(其中c为底面周长,l为棱柱侧棱长)仅适用于正棱柱。
A. 棱柱侧
B.在棱柱
ABC−A'B'C'
中,
V
A'−ABC
=V
B'−ABC;
1
S = ch(其中c为底面周长,h为斜高)
C .在正棱锥P−ABC中, 侧 2 ;
D.棱锥的体积是棱柱体积的三分之一。
【答案】BC
【解析】直棱柱的侧面积是底面周长乘以侧棱长,选项A错;根据棱锥的体积公式可知选项B正确;选项
C正确;等底等高的棱锥体积是棱柱体积的三分之一,选项D错。故选BC。
6.(多选题)如图,直三棱柱 中, , , ,侧面
中心为O,点E是侧棱 上的一个动点,有下列判断,正确的是( )
A.直三棱柱侧面积是 B.直三棱柱体积是
C.三棱锥 的体积为定值 D. 的最小值为格致课堂
【答案】ACD
【解析】在直三棱柱 中, , ,
底面 和 是等腰直角三角形,侧面全是矩形,所以其侧面积为1×2×2+
,故A正确;
直三棱柱的体积为 ,故B不正确;
由BB∥平面AAC C,且点E是侧棱 上的一个动点, 三棱锥 的高为定值 ,
1 1 1
× ×2= , × × = ,故C正确;
设BE=x ,则BE=2﹣x,在 和 中,∴ = .
1
由其几何意义,
即平面内动点(x,1)与两定点(0,0),(2,0)距离和的最小值,由对称可知,当 为 的中点时,
其最小值为 ,故D正确.
故选:ACD.
三、填空题
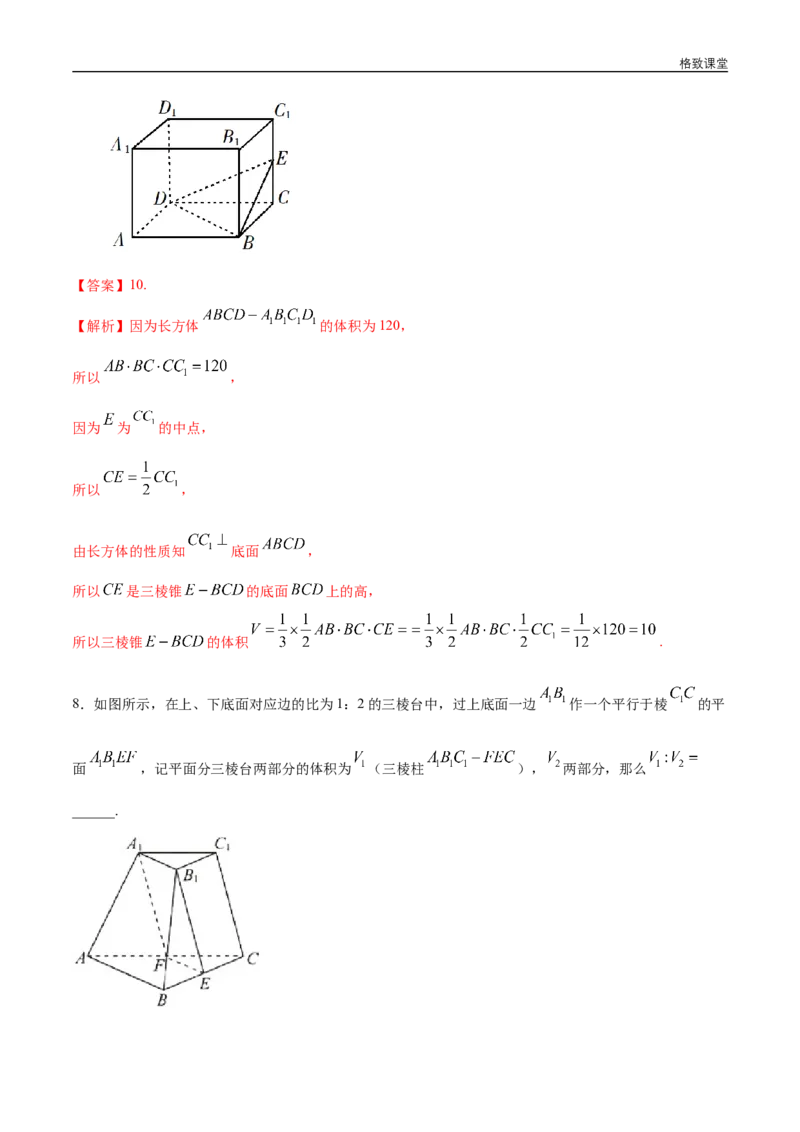
7.【2019年江苏省高考数学试卷】如图,长方体 的体积是120,E为 的中点,则
三棱锥E-BCD的体积是_____.格致课堂
【答案】10.
【解析】因为长方体 的体积为120,
所以 ,
因为 为 的中点,
所以 ,
由长方体的性质知 底面 ,
所以 是三棱锥 的底面 上的高,
所以三棱锥 的体积 .
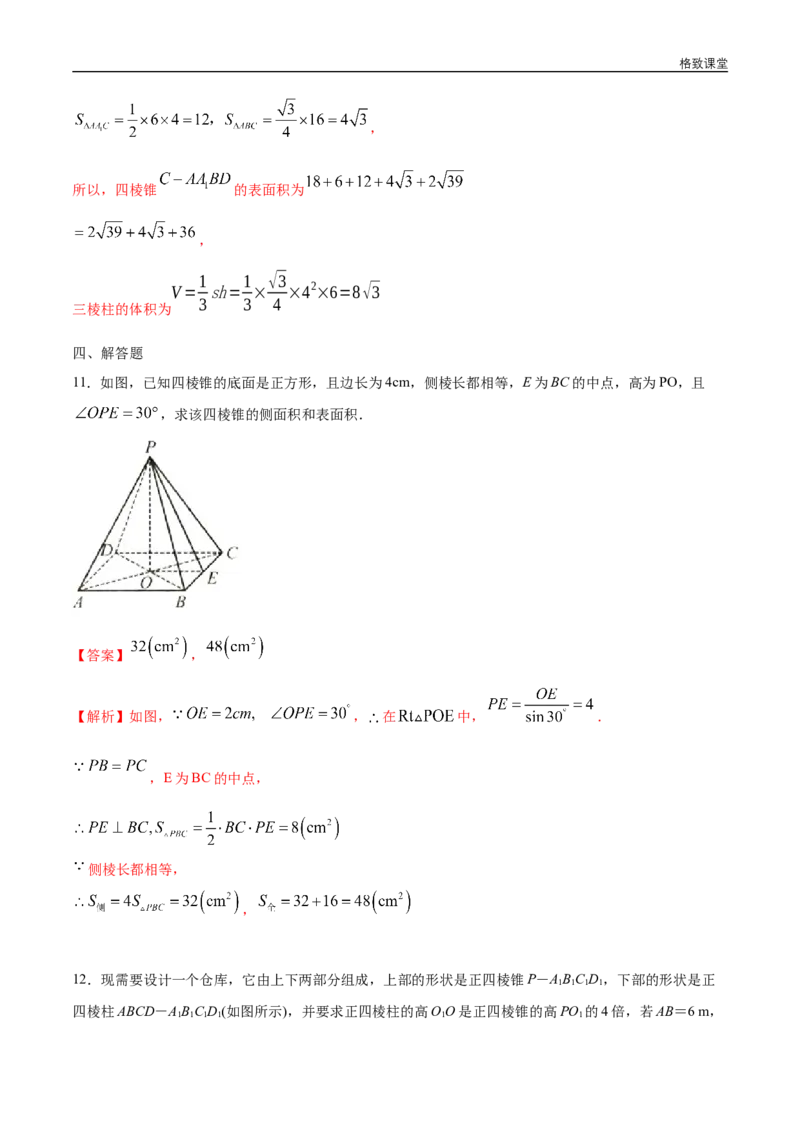
8.如图所示,在上、下底面对应边的比为1:2的三棱台中,过上底面一边 作一个平行于棱 的平
面 ,记平面分三棱台两部分的体积为 (三棱柱 ), 两部分,那么
______.格致课堂
【答案】3:4
【解析】设三棱台的高为 ,上底面的面积是 ,则下底面的面积是 ,
, .
故答案为: ..
9.正六棱柱的高为 ,最长的对角线为 ,则它的侧面积为______.
【答案】
【解析】设正六棱柱的底面边长为 ,
则底面上最长对角线长为 ,
所以由 ,解得 ,
所以侧面积为 .
故答案为
10.【五省优创名校2019届高三联考(全国I卷)数学(文)试题】
已知正三棱柱ABC—A B C 的高为6,AB=4,点D为棱BB 的中点,则四棱锥C—AABD的表面积是
1 1 1 1 1
________,三棱柱的体积为 。
8√3
【答案】
【解析】 正三棱柱的高为6, ,
四棱锥 的表面 为等腰三角形,
, 到 距离为 ,
,
梯形 的面积为 , ,格致课堂
,
所以,四棱锥 的表面积为
,
1 1 √3
V= sh= × ×42 ×6=8√3
3 3 4
三棱柱的体积为
四、解答题
11.如图,已知四棱锥的底面是正方形,且边长为4cm,侧棱长都相等,E为BC的中点,高为PO,且
,求该四棱锥的侧面积和表面积.
【答案】 ,
【解析】如图, , 在 中, .
,E为BC的中点,
侧棱长都相等,
,
12.现需要设计一个仓库,它由上下两部分组成,上部的形状是正四棱锥P-ABC D,下部的形状是正
1 1 1 1
四棱柱ABCD-ABC D(如图所示),并要求正四棱柱的高OO是正四棱锥的高PO 的4倍,若AB=6 m,
1 1 1 1 1 1格致课堂
PO=2 m,则仓库的容积是多少?
1
【答案】
【解析】由PO=2 m,知OO=4PO=8 m.因为AB=AB=6 m,所以正四棱锥P-ABC D 的体积V =
1 1 1 1 1 1 1 1 1 锥
· ·PO= ×62×2=24(m3);
1
正四棱柱ABCD-ABC D 的体积
1 1 1 1
V =AB2·OO=62×8=288(m3),
柱 1
所以仓库的容积V=V +V =24+288=312(m3).
锥 柱
故仓库的容积是312 m3.