文档内容
格致课堂
8.6.2 直线与平面垂直
第 1 课时 直线与平面垂直的判定
一、选择题
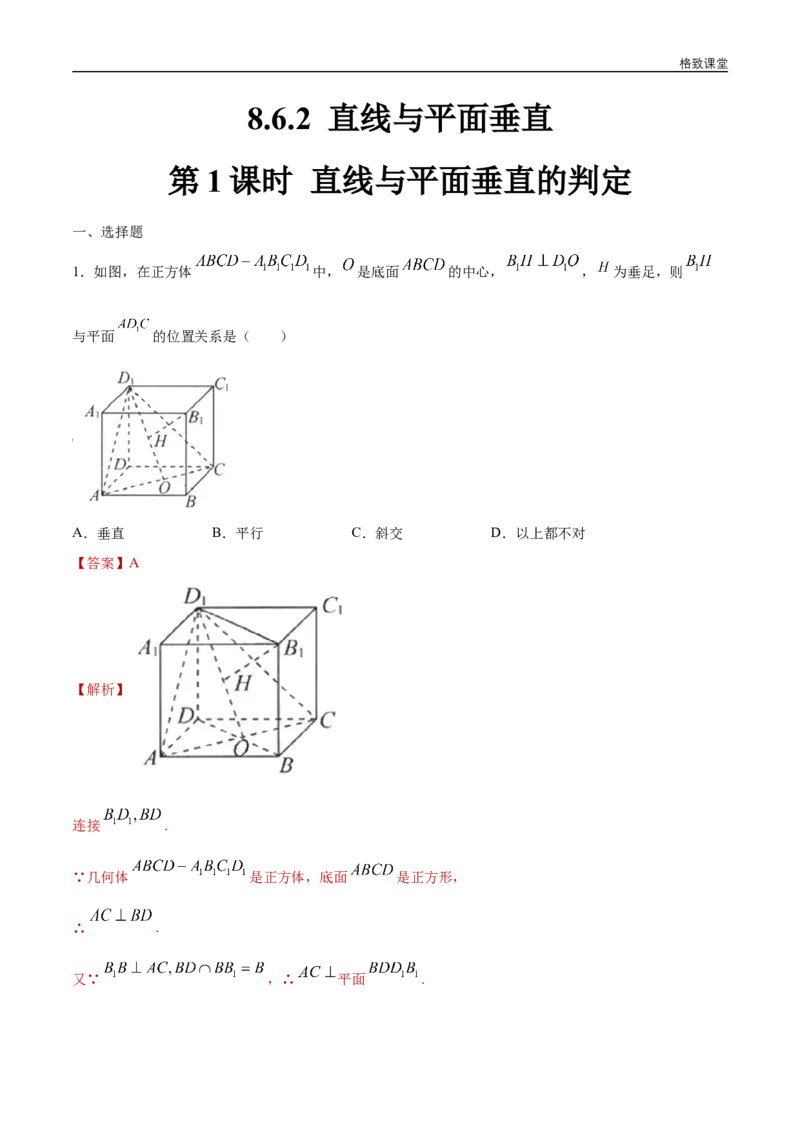
1.如图,在正方体 中, 是底面 的中心, , 为垂足,则
与平面 的位置关系是( )
A.垂直 B.平行 C.斜交 D.以上都不对
【答案】A
【解析】
连接 .
∵几何体 是正方体,底面 是正方形,
∴ .
又∵ ,∴ 平面 .格致课堂
∵ 平面 ,∴ .
∵ ,∴ 平面 .
故选A.
2.若斜线段 是它在平面 上的射影长的2倍,则 与平面 所成的角是( )
A. B. C. D.
【答案】A
【解析】如图所示,作点 在平面 上的射影 ,连接 ,
则 即是斜线 与平面 所成的角,且 为直角三角形.
又 ,所以 ,
所以 .
故选A.
3.正方体 中, 与平面 所成的角为( )
A. B. C. D.
【答案】A
【解析】如图,连接 交 于点E,连接AE,格致课堂
正方体中,证得: 平面 ,
所以 与平面 所成的角为 ,
设正方体的边长为 ,
在 中,求得: , ,
,所以 ,
故选:A
4.如图所示的正方形 中, 分别是 , 的中点,现沿 , , 把这个正方
形折成一个四面体,使 , , 重合为点 ,则有( )
A. 平面 B. 平面
C. 平面 D. 平面
【答案】A
【解析】由题意: , ,格致课堂
, 平面
所以 平面 正确,D不正确;.
又若 平面 ,则 ,由平面图形可知显然不成立;
同理 平面 不正确;
故选:A
5.(多选题)如图,在以下四个正方体中,直线 与平面 垂直的是( )
A. B.
C. D.
【答案】BD
【解析】对于A,由 与 所成角为 ,
可得直线 与平面 不垂直;
对于B,由 , , ,
可得 平面 ;
对于C,由 与 所成角为 ,
可得直线 与平面 不垂直;
对于D,连接 ,由 平面 ,
可得 ,同理可得 ,
又 ,所以 平面 .
故选:BD
6.(多选题)如果一条直线垂直于一个平面内的:
①三角形的两边;②梯形的两边;③圆的两条直径;④正五边形的两边.格致课堂
那么能保证该直线与平面垂直的是( )
A.① B.② C.③ D.④
【答案】ACD
【解析】根据直线与平面垂直的判定定理,平面内这两条直线必须是相交的;
选项A、C、D中给定的两条直线一定相交,能保证直线与平面垂直;而B中梯形的两边可能是上、下底
边,它们互相平行,不满足定理条件.
故选:ACD.
二、填空题
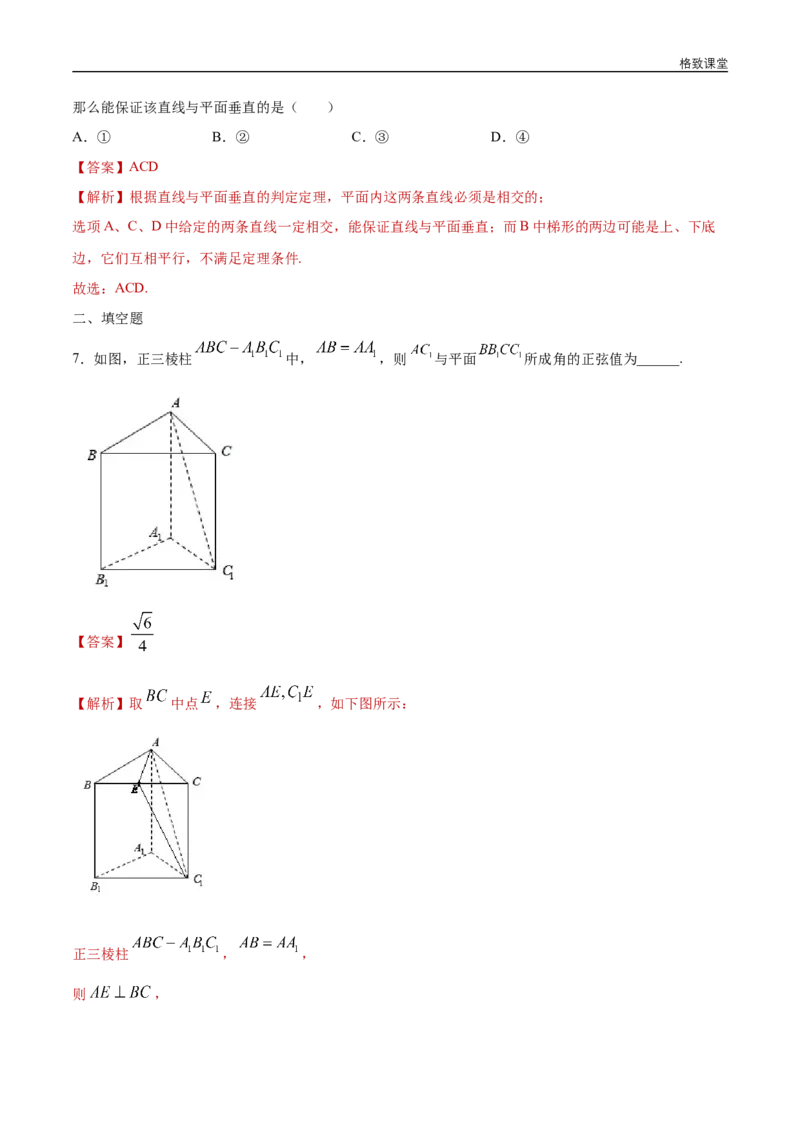
7.如图,正三棱柱 中, ,则 与平面 所成角的正弦值为______.
【答案】
【解析】取 中点 ,连接 ,如下图所示:
正三棱柱 , ,
则 ,格致课堂
因为 平面 ,
平面 ,所以
而 ,则 平面 ,
则 即为 与平面 所成角.
因为 ,
所以
故答案为: .
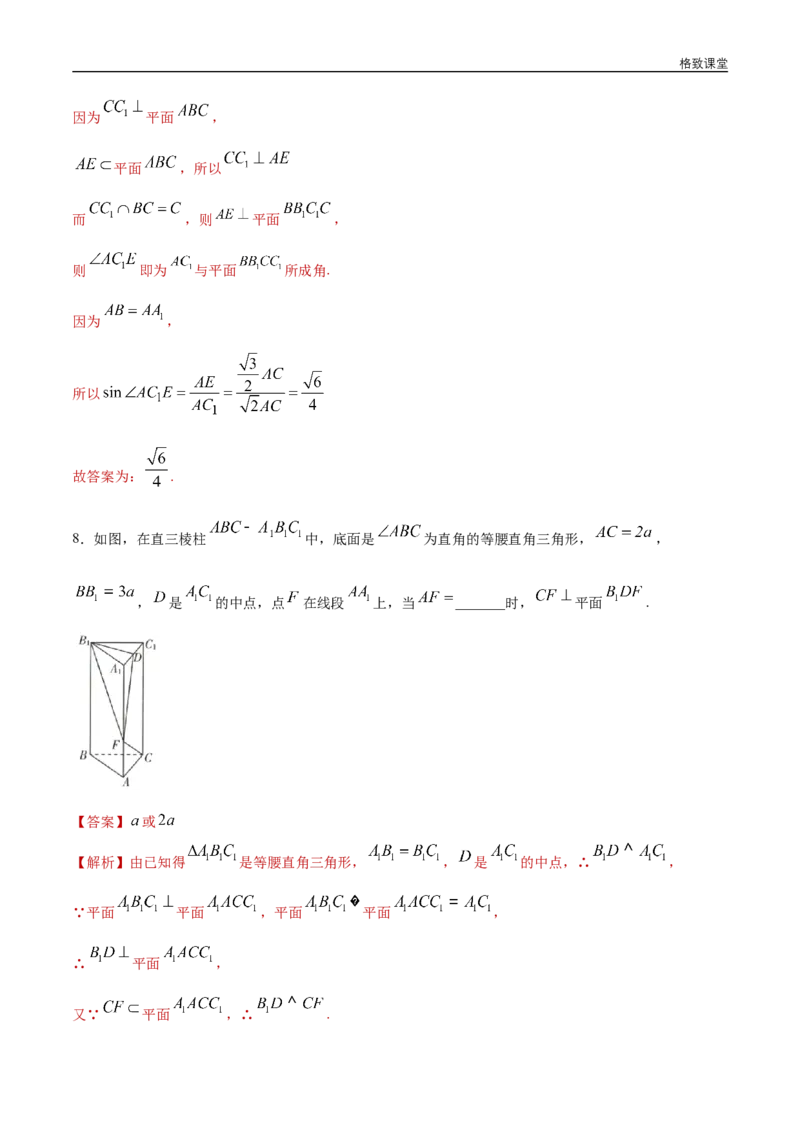
8.如图,在直三棱柱 中,底面是 为直角的等腰直角三角形, ,
, 是 的中点,点 在线段 上,当 _______时, 平面 .
【答案】 或
【解析】由已知得 是等腰直角三角形, , 是 的中点,∴ ,
∵平面 平面 ,平面 平面 ,
∴ 平面 ,
又∵ 平面 ,∴ .格致课堂
若 平面 ,则 .
设 ,则 ,
,
∴ ,
解得 或 .
9.已知平面 和直线 ,给出条件:
① ;② ;③ ;④ ;⑤ .
(1)当满足条件 时,有 ;
(2)当满足条件 时,有 .(填所选条件的序号)
【答案】③⑤;②⑤
【解析】
试题分析:若m α,α∥β,则m∥β;
若m⊥α,α∥β,⊂则m⊥β.
故答案为(1)③⑤(2)②⑤
10.已知三棱锥S-ABC中,底面ABC为边长等于2的等边三角形,SA垂直于底面ABC,SA=3,那么直线
AB与平面SBC所成角的正弦值为________.
【答案】
【解析】 如图所示,取BC的中点D,连接SD,AD,则BC⊥AD.
过点A作AG⊥SD于点G,连接GB.
∵SA⊥底面ABC,BC 平面ABC,
⊂格致课堂
∴BC⊥SA,又SA∩AD=A,
∴BC⊥平面SAD.
又AG 平面SAD,∴AG⊥BC.
又AG⊂⊥SD,SD∩BC=D,∴AG⊥平面SBC.
∴∠ABG即为直线AB与平面SBC所成的角.
∵AB=2,SA=3,∴AD=,SD=2.
在Rt SAD中,AG==.
∴sin△∠ABG===.
三、解答题
11.如图,在四棱锥 中, 平面 , , , , ,
, .
(I)求异面直线 与 所成角的余弦值;
(II)求证: 平面 ;
(Ⅲ)求直线 与平面 所成角的正弦值.
【答案】(Ⅰ) .(Ⅱ)见解析;(Ⅲ) .
【解析】(Ⅰ)如图,由已知AD//BC,故 或其补角即为异面直线AP与BC所成的角.
因为AD⊥平面PDC,所以AD⊥PD.
在Rt PDA中,由已知,得 ,
△格致课堂
故 .
所以,异面直线AP与BC所成角的余弦值为 .
(Ⅱ)证明:因为AD⊥平面PDC,直线PD 平面PDC,所以AD⊥PD.
又因为BC//AD,所以PD⊥BC,
又PD⊥PB,
所以PD⊥平面PBC.
(Ⅲ)过点D作AB的平行线交BC于点F,连结PF,
则DF与平面PBC所成的角等于AB与平面PBC所成的角.
因为PD⊥平面PBC,故PF为DF在平面PBC上的射影,
所以 为直线DF和平面PBC所成的角.
由于AD//BC,DF//AB,故BF=AD=1,
由已知,得CF=BC–BF=2.
又AD⊥DC,故BC⊥DC,
在Rt DCF中,可得 ,
△
在Rt DPF中,可得 .
△
所以,直线AB与平面PBC所成角的正弦值为 .
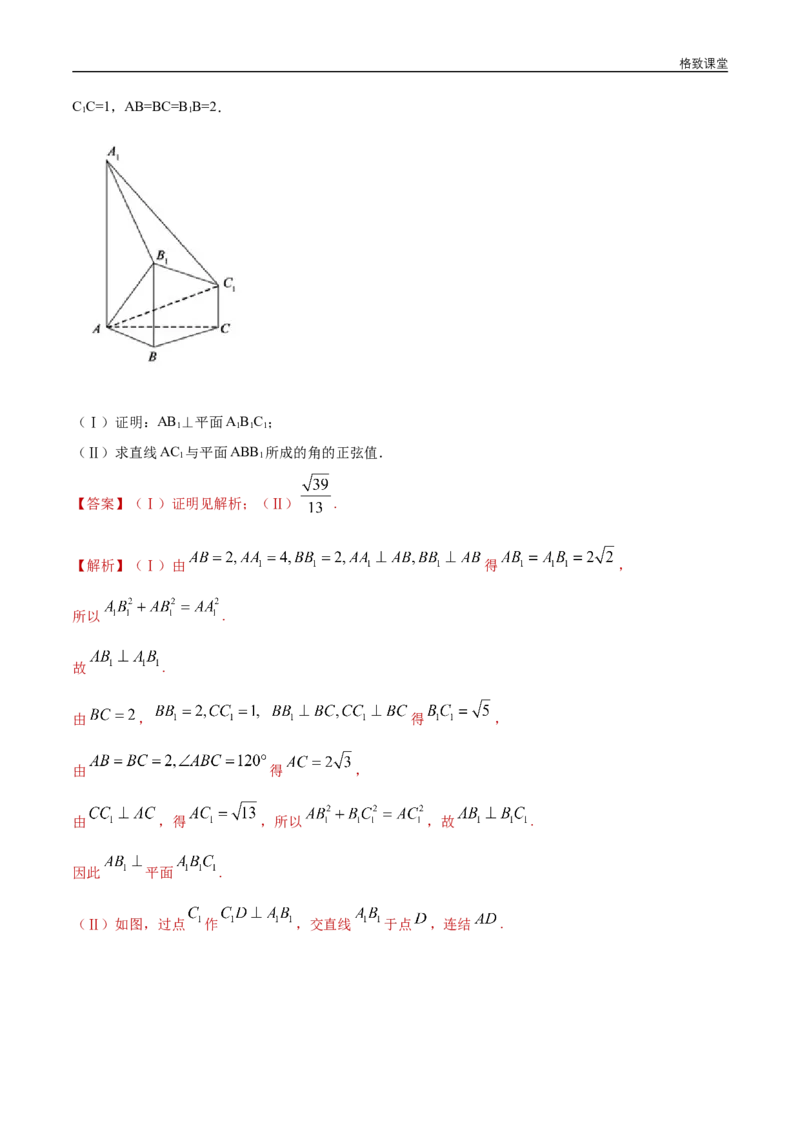
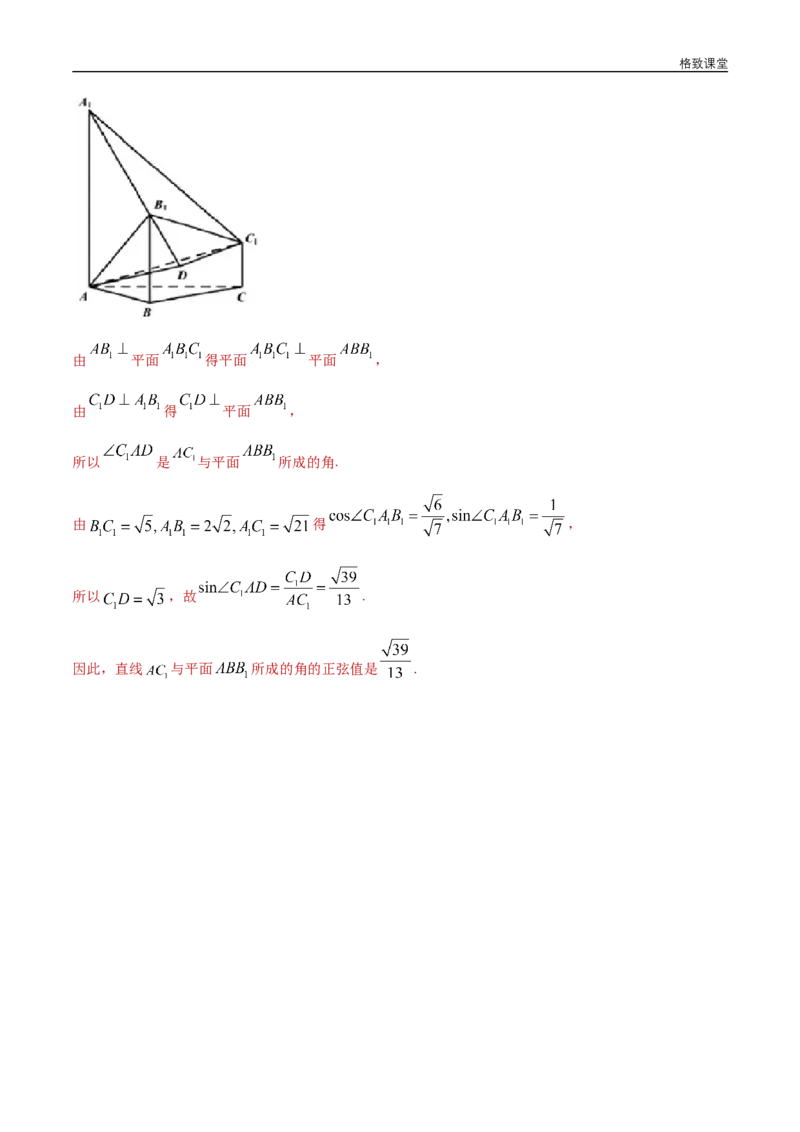
12.如图,已知多面体ABC-A B C ,AA,B B,C C均垂直于平面ABC,∠ABC=120°,AA=4,
1 1 1 1 1 1 1格致课堂
C C=1,AB=BC=B B=2.
1 1
(Ⅰ)证明:AB ⊥平面AB C ;
1 1 1 1
(Ⅱ)求直线AC 与平面ABB 所成的角的正弦值.
1 1
【答案】(Ⅰ)证明见解析;(Ⅱ) .
【解析】(Ⅰ)由 得 ,
所以 .
故 .
由 , 得 ,
由 得 ,
由 ,得 ,所以 ,故 .
因此 平面 .
(Ⅱ)如图,过点 作 ,交直线 于点 ,连结 .格致课堂
由 平面 得平面 平面 ,
由 得 平面 ,
所以 是 与平面 所成的角.
由 得 ,
所以 ,故 .
因此,直线 与平面 所成的角的正弦值是 .