文档内容
格致课堂
8.6.3 平面与平面垂直
第 1 课时 平面与平面垂直的判定
一、选择题
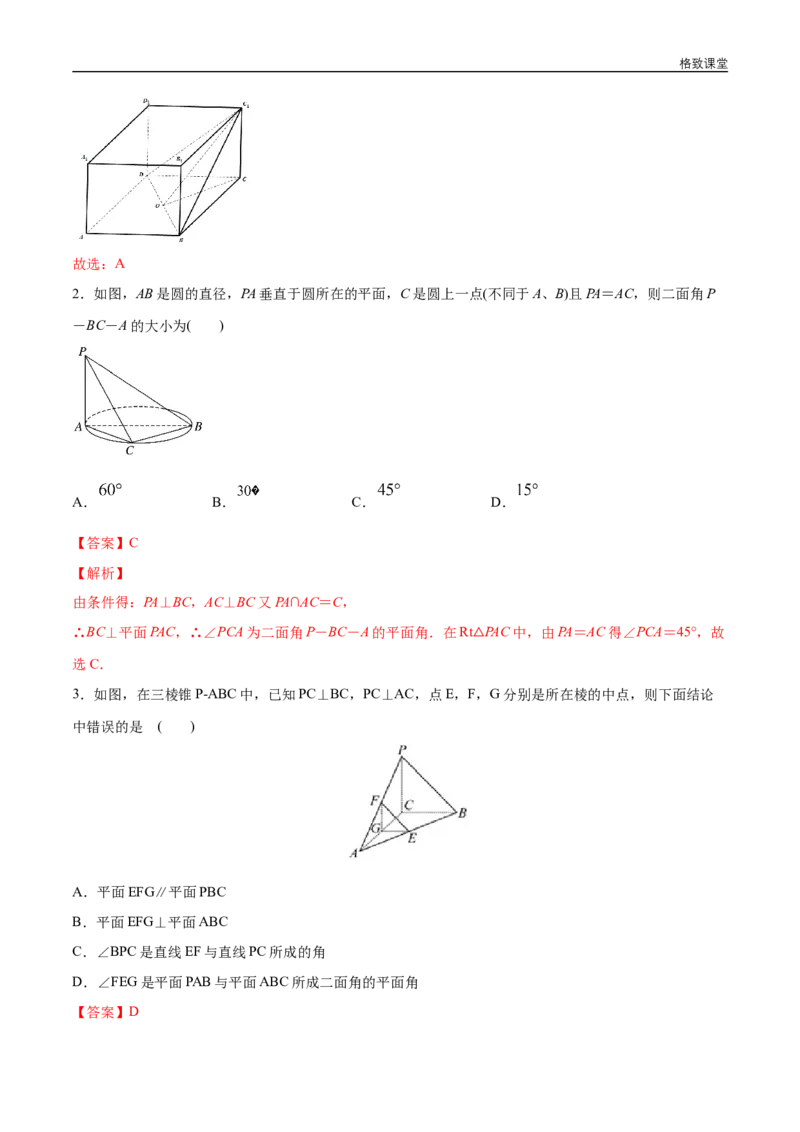
1.在长方体 中, , ,则二面角 的大小是(
)
A.30º B.45º C.60º D.90º
【答案】A
【解析】由题意,作出长方体 的图象,
取 中点为 ,连接 、 ,
因为 平面 ,所以 即 在平面 上的投影,
又 平面 ,所以 ,
因为 ,所以四边形 是正方形,
为 中点,所以 ,又 ,
所以 平面 ,又 平面 ,所以 ,
即二面角 ,
又 , ,
所以 , .格致课堂
故选:A
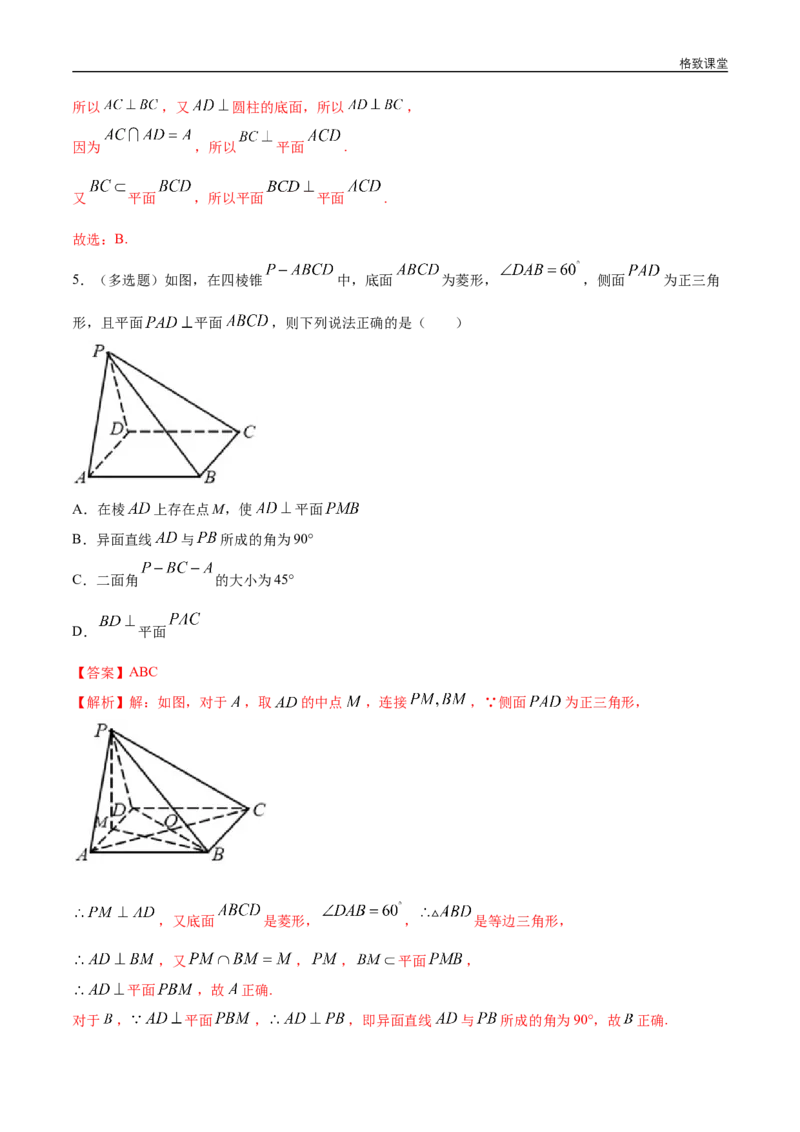
2.如图,AB是圆的直径,PA垂直于圆所在的平面,C是圆上一点(不同于A、B)且PA=AC,则二面角P
-BC-A的大小为( )
A. B. C. D.
【答案】C
【解析】
由条件得:PA⊥BC,AC⊥BC又PA∩AC=C,
∴BC⊥平面PAC,∴∠PCA为二面角P-BC-A的平面角.在Rt PAC中,由PA=AC得∠PCA=45°,故
选C. △
3.如图,在三棱锥P-ABC中,已知PC⊥BC,PC⊥AC,点E,F,G分别是所在棱的中点,则下面结论
中错误的是 ( )
A.平面EFG∥平面PBC
B.平面EFG⊥平面ABC
C.∠BPC是直线EF与直线PC所成的角
D.∠FEG是平面PAB与平面ABC所成二面角的平面角
【答案】D格致课堂
【解析】对于A,因为点E,F分别是AB,AP的中点,
所以 ,
又 平面 , 平面 ,
所以 平面 .同理 平面 ,
又 ,
所以平面 平面 .因此A正确.
对于B,因为 ,
所以 平面 .
又 ,
所以 平面 ,
又 平面 ,
所以平面 平面 .因此B正确.
对于C,由于平面 平面 ,且与平面PAB交于EF,PB,∴
所以∠BPC是直线EF与直线PC所成的角.因此C正确.
对于D,由于FE,GE与AB不垂直,所以∠FEG不是平面PAB与平面ABC所成二面角的平面角,因此D
不正确.
综上选项D不正确.选D.
4.已知 是圆柱上底面的一条直径, 是上底面圆周上异于 , 的一点, 为下底面圆周上一点,
且 圆柱的底面,则必有( )
A.平面 平面 B.平面 平面
C.平面 平面 D.平面 平面
【答案】B
【解析】因为 是圆柱上底面的一条直径,格致课堂
所以 ,又 圆柱的底面,所以 ,
因为 ,所以 平面 .
又 平面 ,所以平面 平面 .
故选:B.
5.(多选题)如图,在四棱锥 中,底面 为菱形, ,侧面 为正三角
形,且平面 平面 ,则下列说法正确的是( )
A.在棱 上存在点M,使 平面
B.异面直线 与 所成的角为90°
C.二面角 的大小为45°
D. 平面
【答案】ABC
【解析】解:如图,对于 ,取 的中点 ,连接 ,∵侧面 为正三角形,
,又底面 是菱形, , 是等边三角形,
,又 , , 平面 ,
平面 ,故 正确.
对于 , 平面 , ,即异面直线 与 所成的角为90°,故 正确.格致课堂
对于 ,∵平面 平面 , , 平面 , ,
是二面角 的平面角,设 ,则 , ,
在 中, ,即 ,故二面角 的大小为45°,故
正确.
对于 ,因为 与 不垂直,所以 与平面 不垂直,故 错误.
故选:
6.(多选题)如图,梯形ABCD中,AD//BC,AD=AB=1,AD⊥AB,∠BCD=45°,将ΔABD
沿对角线BD折起.设折起后点A的位置为A',并且平面A'BD⊥平面BCD.给出下面四个命题正确的:()
√2
A.A'D⊥BC B.三棱锥A'-BCD的体积为
2
C.CD⊥平面A'BD D.平面A'BC⊥平面A'DC
【答案】CD
【解析】如图所示:E为BD中点,连接A'E
AD//BC,AD=AB=1,AD⊥AB得到∠DBC=∠ADB=45°
又∠BCD=45°故ΔBCD为等腰直角三角形
平面A'BD⊥平面BCD,CD⊥BD ,所以CD⊥平面A'BD,所以C正确
E为BD中点,A'E⊥BD则A'E⊥平面BCD 所以A'E⊥BC
如果A'D⊥BC,则可得到BC⊥平面A'BD,故BC⊥BD 与已知矛盾.故A错误
1 1 √2 √2
三棱锥A'-BCD的体积为S= × ×√2×√2× = .故B错误
3 2 2 6
在直角三角形A'CD中,A'C2=CD2+A'D2∴A'C=√3
在三角形A'BC中,A'B=1,BC=2,A'C=√3 满足BC2=A'B2+A'C2∴BA'⊥CA'
又BA'⊥DA' 所以BA'⊥平面A'DC,所以平面A'BC⊥平面A'DC,故D正确
综上所述:答案为CD格致课堂
三、填空题
7.在长方体 中, , ,则平面 与平面 所成的二面角的正
弦值是_________.
【答案】
【解析】画出图像如下图所示,将平面 延展成平面 ,将平面 延展成平面 ,
平面 与平面 相交于 ,且 ,所以 是平面 与平
面 所成的二面角.在 中 ,所以 .
故答案为:
8.如图,在四棱锥 中, 底面 且底面各边都相等, 是 上一点, 当点
满足 时,平面 平面 (只要填写一个你认为正确的条件即可)格致课堂
【答案】DM⊥PC(或BM⊥PC)
【解析】连接 ,因为 底面 ,所以 ,因为四边形 的各边相等,所以
,且 ,所以 平面 ,即 ,要使平面 平面 ,只需
垂直于面 上的与 相交的直线即可,所以可填 ;故填
.
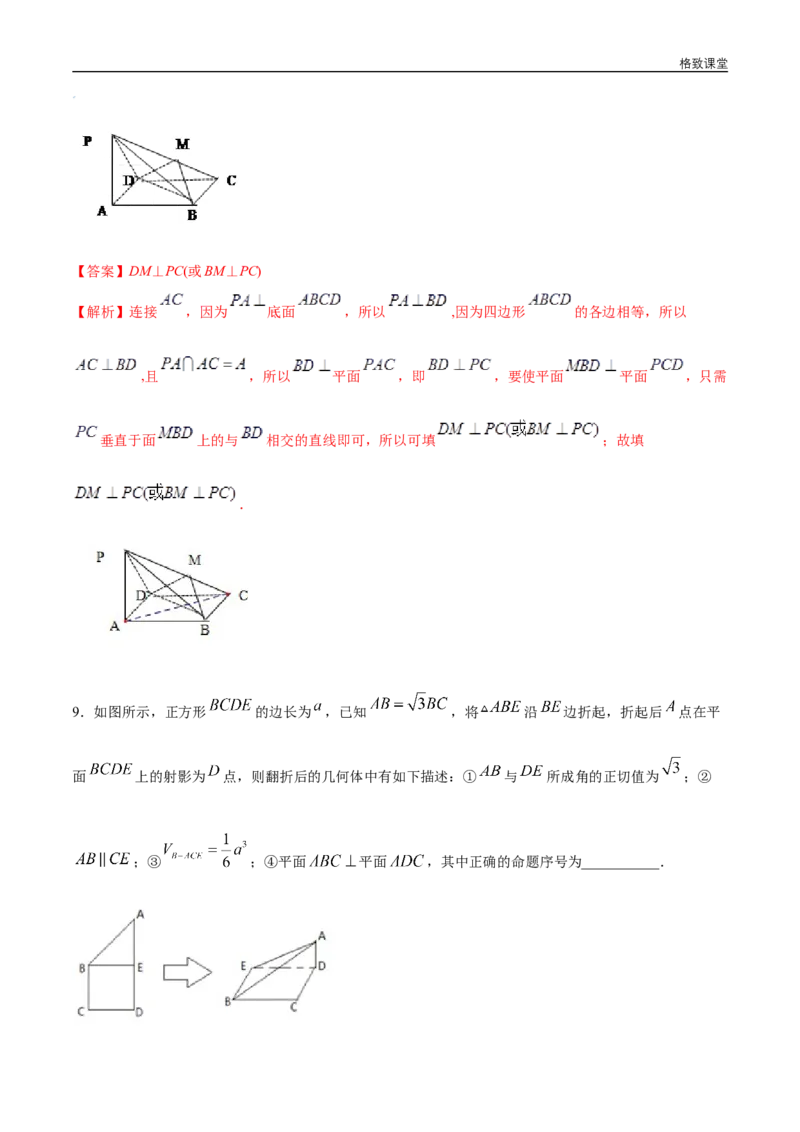
9.如图所示,正方形 的边长为 ,已知 ,将 沿 边折起,折起后 点在平
面 上的射影为 点,则翻折后的几何体中有如下描述:① 与 所成角的正切值为 ;②
;③ ;④平面 平面 ,其中正确的命题序号为___________.格致课堂
【答案】③④
【解析】
作出折叠后的几何体直观图如图所示:
∵AB= a,BE=a,∴AE= a.
∴ .
∵BC∥DE,∴∠ABC是异面直线AB,DE所成的角,
在Rt ABC中, ,故①不正确;
△
连结BD,CE,则CE⊥BD,
又AD⊥平面BCDE,CE 平面BCDE,
∴CE⊥AD,又BD∩AD=⊂D,BD 平面ABD,AD 平面ABD,
∴CE⊥平面ABD,又AB 平面A⊂BD, ⊂
∴CE⊥AB.故②错误. ⊂
三棱锥B−ACE的体积 .
故③正确.
∵AD⊥平面BCDE,BC 平面BCDE,
∴BC⊥AD,又BC⊥CD⊂,
∴BC⊥平面ACD,∵BC 平面ABC,
∴平面ABC⊥平面ACD.⊂
故答案为③④.
10.如图所示,在长方体中 ,棱 与棱 的位置关系是_________,棱 与平面
的位置关系是__________,平面 与平面 的位置关系是_________.格致课堂
【答案】平行 垂直 垂直
【解析】根据长方体的性质可知,棱 与棱 平行,棱 与DC,DH垂直,所以棱 与平面
垂直,长方体的侧面与底面垂直,故平面 与平面 垂直.
三、解答题
11.已知四棱锥 的底面 是菱形, , 的中点 是顶点 在底面
的射影, 是 的中点.
(1)求证:平面 平面 ;
(2)若 ,直线 与平面 所成角的正弦值.
【答案】(1)见解析(2)
【解析】 (1)证明 ∵四边形ABCD是菱形,∠ADC=120°,
且M是AD的中点,∴MB⊥AD,∴MB⊥BC.
又∵P在底面ABCD的射影M是AD的中点,
∴PM⊥平面ABCD,
又∵BC 平面ABCD,∴PM⊥BC,
而PM∩⊂MB=M,PM,MB 平面PMB,
⊂格致课堂
∴BC⊥平面PMB,又BC 平面PBC,
∴平面MPB⊥平面PBC. ⊂
(2)解 过点B作BH⊥MC,连接HN,
∵PM⊥平面ABCD,BH 平面ABCD,∴BH⊥PM,
又∵PM,MC 平面PMC⊂,PM∩MC=M,
∴BH⊥平面P⊂MC,
∴HN为直线BN在平面PMC上的射影,
∴∠BNH为直线BN与平面PMC所成的角,
在菱形ABCD中,设AB=2a,则MB=AB·sin 60°= a,
MC= = a.
又由(1)知MB⊥BC,
∴在 MBC中,BH= = a,
△
由(1)知BC⊥平面PMB,PB 平面PMB,
⊂
∴PB⊥BC,∴BN= PC= a,
∴sin∠BNH= = = .
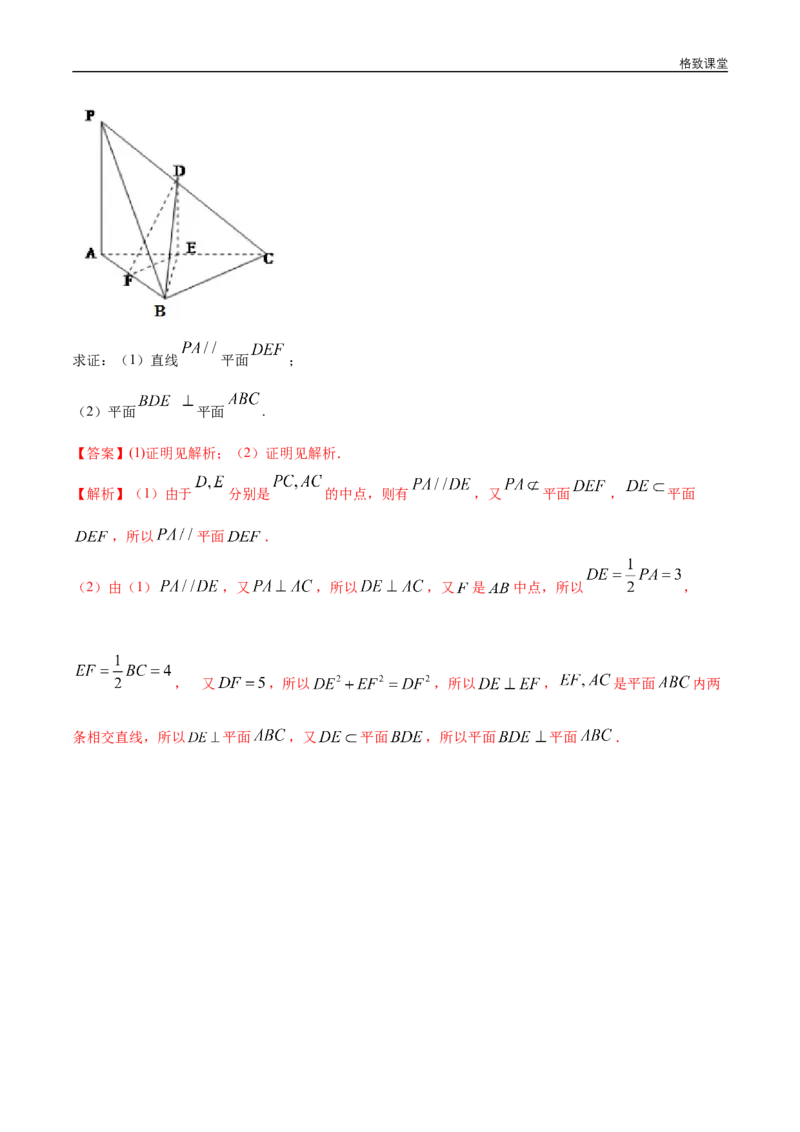
12.如图在三棱锥 中, 分别为棱 的中点,已知
.格致课堂
求证:(1)直线 平面 ;
(2)平面 平面 .
【答案】(1)证明见解析;(2)证明见解析.
【解析】(1)由于 分别是 的中点,则有 ,又 平面 , 平面
,所以 平面 .
(2)由(1) ,又 ,所以 ,又 是 中点,所以 ,
, 又 ,所以 ,所以 , 是平面 内两
条相交直线,所以 平面 ,又 平面 ,所以平面 平面 .