文档内容
新高考地区高 2024 届高二(上)期中模拟试题二
数学试卷
注意事项:
1.答题前,考生务必将自己的姓名、准考证号、班级、学校在答题卡上填写清楚.
2.每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦
干净后,再选涂其他答案标号.在试卷上作答无效.
3.考试结束后,请将答题卡交回,试卷自行保存.满分150分,考试用时120分钟.
一、单选题:本题共8小题,每小题5分,共40分.在每个小题给出的四个选项中,只有一项
是符合题目要求的.
1.直线 的倾斜角为( )
A. B. C. D.
2.已知 为直线l的方向向量, 、 分别为平面 、 的法向量( 、 不重合),那么下列说法中:
① ;② ;③ ;④ .其中正确的有( ).
A.1个 B.2个 C.3个 D.4个
3.设甲:实数 ;乙:方程 是圆,则甲是乙的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
4.抛物线 的焦点到圆 上点的距离的最大值为( )
A.6 B.2 C.5 D.8
5.若正三棱柱 的所有棱长都相等,D是 的中点,则直线AD与平面 所成角的正弦
值为( )
A. B. C. D.6.设圆 的圆心为C,直线l过点 ,且与圆C交于A,B两点,若 ,
则直线l的方程为( )
A. B. 或
C.x=0 D.x=0或
7.已知 分别为双曲线 的左、右顶点,点P为双曲线C上任意一点,记直线
,直线 的斜率分别为 .若 ,则双曲线C的离心率为( )
A. B. C.2 D.
8.已知 是椭圆 上的动点,且与 的四个顶点不重合, , 分别是椭圆的左、右焦点,若
点 在 的平分线上,且 ,则 的取值范围是( )
A. B. C. D.
二、多选题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目
要求,全部选对的得5分,部分选对的得2分,有选错的得0分.
9.下列结论正确的是( )
A.过点 且在两坐标轴上的截距相等的直线l的方程为 ;
B.圆 上有且仅有3个点到直线 的距离都等于1
C.已知 ,O为坐标原点,点 是圆 外一点,且直线m的方程是 ,则
直线m与圆E相交;
D.已知直线 和以 , 为端点的线段相交,则实数k的取值范围为 ;
10.如图,已知 , 分别是正方体 的棱 和 的中点,则( )A. 与 是异面直线
B. 与 所成角的大小为
C. 与平面 所成角的余弦值为
D.二面角 的余弦值为
11.(多选)已知抛物线 的焦点 到准线的距离为 ,直线 过点 且与抛物线交于
, 两点,若 是线段 的中点,则( )
A. B.抛物线的方程为
C.直线 的方程为 D.
12.已知 、 分别为双曲线 的左、右焦点,且 ,点P为双曲线右支一点,
I为 的内心,若 成立,则下列结论正确的有( )
A.当 轴时, B.离心率
C. D.点I的横坐标为定值a
三、填空题:本题共4小题,每小题5分,共20分.13.若直线m被两平行线 与 所截得的线段的长为 ,则m的倾斜角可以是
①15°,②30°,③45°,④60°,⑤75°.其中正确答案的序号是_____(写出所有正确答案的序号).
14.若直线 与曲线 有两个交点,则实数 的取值范围是______.
15.已知菱形 中, ,沿对角线 折叠之后,使得平面 平面 ,则二面角
的余弦值为______.
16.已知椭圆 与双曲线 有相同的焦点 ,椭圆
的离心率为 ,双曲线 的离心率为 ,点 为椭圆 与双曲线 的第一象限的交点,且 ,
则 的取值范围是___________.
四、解答题:本题共6小题,第17小题10分,其余小题每题12分,共70分.解答题应写出
文字说明、证明过程或演算步骤.
17.已知圆 .
(1)过点 作圆C的切线l,求切线l的方程;
(2)设过点 的直线m与圆C交于AB两点,若点A、B分圆周得两段弧长之比为1:2,求直线m得方程.
18.在平面直角坐标系中,△ABC的三个顶点坐标分别为 , , .
(1)求BC边上的中线AD的所在直线方程;
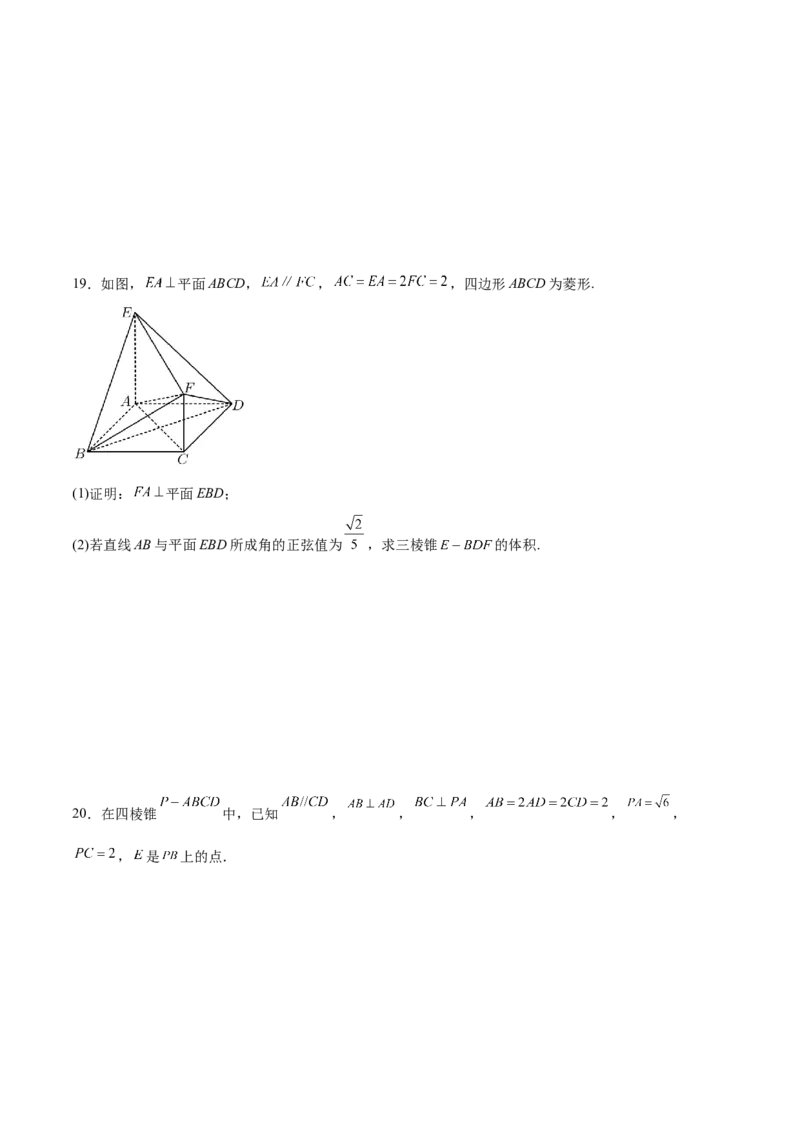
(2)求△ABC的外接圆O被直线l: 截得的弦长.19.如图, 平面ABCD, , ,四边形ABCD为菱形.
(1)证明: 平面EBD;
(2)若直线AB与平面EBD所成角的正弦值为 ,求三棱锥 的体积.
20.在四棱锥 中,已知 , , , , ,
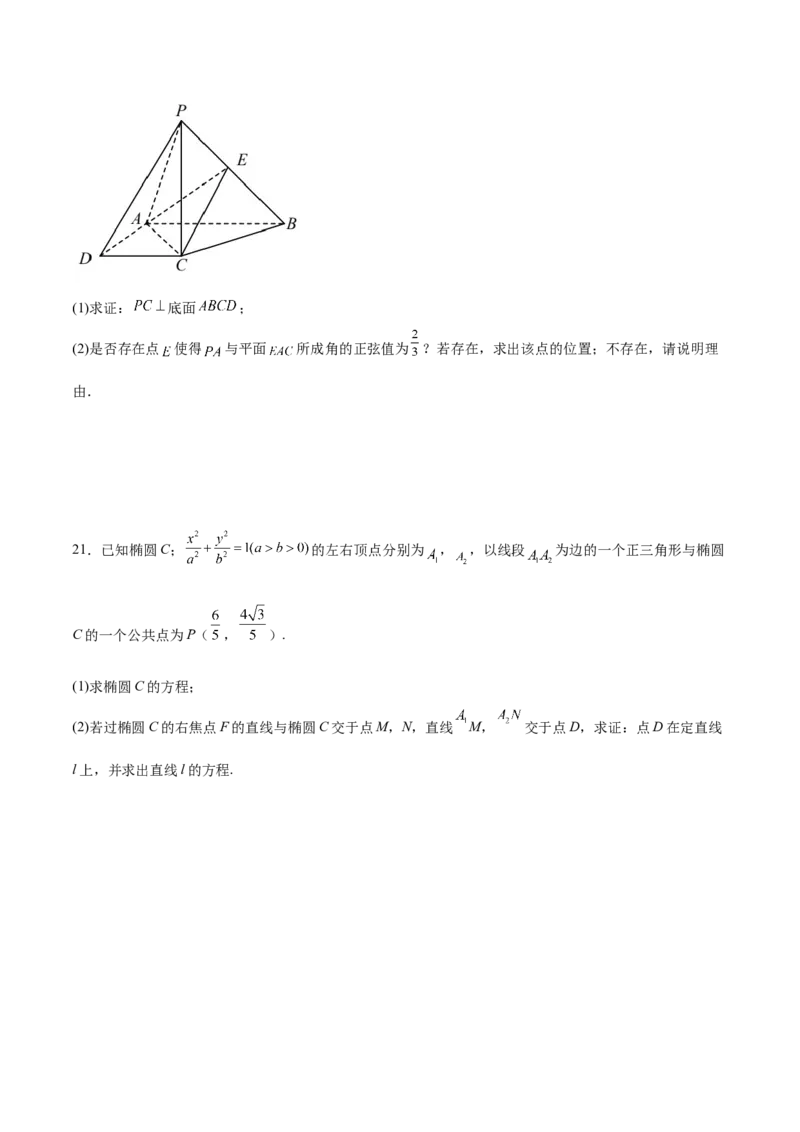
, 是 上的点.(1)求证: 底面 ;
(2)是否存在点 使得 与平面 所成角的正弦值为 ?若存在,求出该点的位置;不存在,请说明理
由.
21.已知椭圆C; 的左右顶点分别为 , ,以线段 为边的一个正三角形与椭圆
C的一个公共点为P( , ).
(1)求椭圆C的方程;
(2)若过椭圆C的右焦点F的直线与椭圆C交于点M,N,直线 M, 交于点D,求证:点D在定直线
l上,并求出直线l的方程.22.在平面直角坐标系 中,设 为椭圆 的左焦点,直线 与 轴交于
点 , 为椭圆 的左顶点,已知椭圆长轴长为8,且 .
(1)求椭圆 的标准方程;
(2)若过点 的直线与椭圆交于两点 、 ,设直线 、 的斜率分别为 、 .
①求证: 为定值;
②求 面积的最大值.