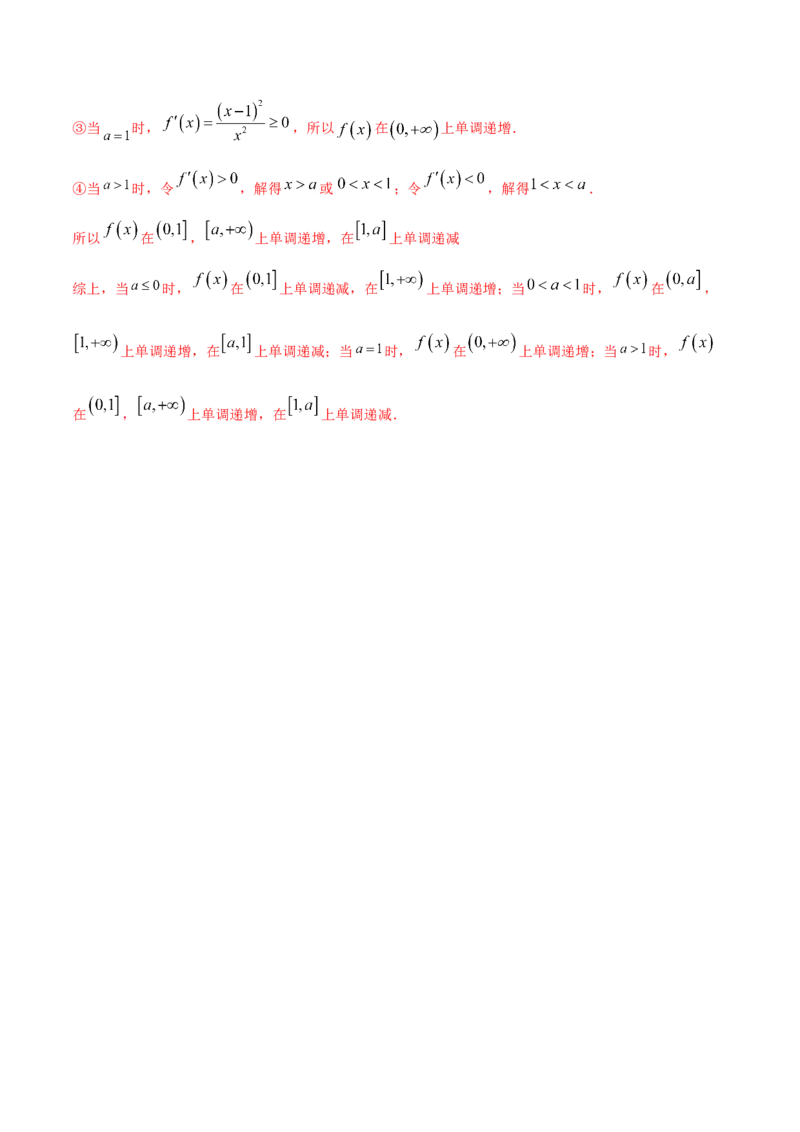文档内容
高二数学期末押题卷(二)
一、单项选择题(本大题共8题,每小题5分,共计40分。每小题列出的四个选项中只有一
项是最符合题目要求的)
1.已知集合 , ,则 ( )
A. B. C. D.
【答案】C
【详解】
, ,
.
故选:C.
2. ( )
A. B. C. D.
【答案】B
【详解】
∵
∴
故选:B
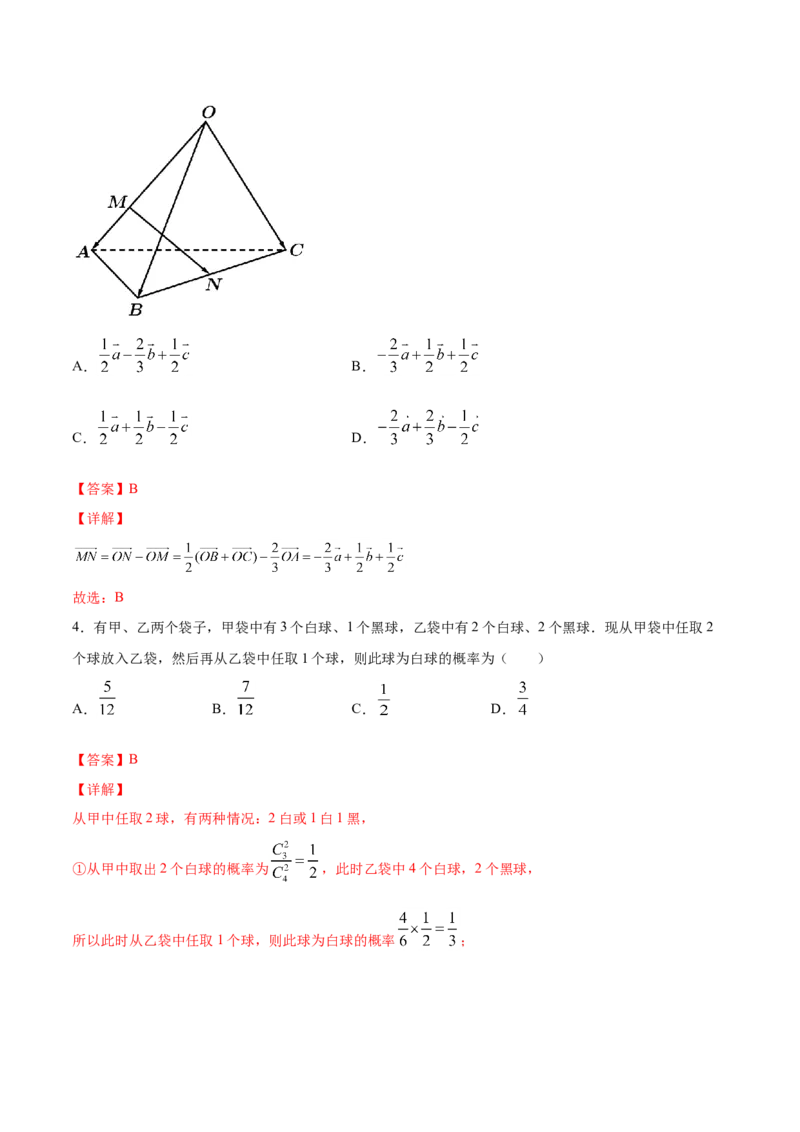
3.如图所示,在空间四边形 中, ,点 在 上,且 ,
为 中点,则 ( )A. B.
C. D.
【答案】B
【详解】
故选:B
4.有甲、乙两个袋子,甲袋中有3个白球、1个黑球,乙袋中有2个白球、2个黑球.现从甲袋中任取2
个球放入乙袋,然后再从乙袋中任取1个球,则此球为白球的概率为( )
A. B. C. D.
【答案】B
【详解】
从甲中任取2球,有两种情况:2白或1白1黑,
①从甲中取出2个白球的概率为 ,此时乙袋中4个白球,2个黑球,
所以此时从乙袋中任取1个球,则此球为白球的概率 ;②从甲中取出1个白球和1个黑球的概率为 ,此时乙袋中3个白球,3个黑球,
所以此时从乙袋中任取1个球,则此球为白球的概率 ,
所以从乙袋中任取1球且此球是白球的概率 .
故选:B.
5.已知 ,则 等于( )
A.11 B.10 C.8 D.1
【答案】A
【详解】
,求导得 ,
则 ,解得 ,
故 ,
,
故选:A.
6.一道试题,甲解出的概率为 ,乙解出的概率为 .设解出该题的人数为X,则D(X)等于( )
A. B.
C. D.
【答案】B
【详解】
依题意X的可能取值为0,1,2,甲乙均未答对时,P(X=0)= ,
甲乙二人一人答对一人答错时,P(X=1)= ,
甲乙均答对时,P(X=2)= .
所以X的分布列为
X 0 1 2
P
所以E(X)=0× +1× +2× = ,
D(X)= .
故选:B.
7.已知函数 在 上是增函数,在[0,2]上是减函数,且方程 有3
个实数根,它们分别是 , ,2,则 的最小值是( )
A.5 B.6 C.7 D.8
【答案】A
【详解】
由 ,求导得 , 在 上是增函数,在[0,2]上
是减函数,
,即 ,此时 的另外一个根为 ,且方程 有3个实数根,它们分
别是 , ,2,,即 ,且 ,所以 ,
化简函数 ,
所以 则 ,
所以 ,因为 ,所以 ,所以
的最小值是5.
8.红外线自动测温门能有效避免测温者与被测温者的近距离接触,降低潜在的病毒感染风险.为防控新冠
肺炎,某厂生产的红外线自动测温门,其测量体温误差服从正态分布 ,从已经生产出的测温
门中随机取出一件,则其测量体温误差在区间 内的概率为( )
(附:若随机变量 服从正态分布 ,则 ,
)
A. B. C. D.
【答案】C
【详解】
由题意可知
则
,二、多项选择题(本大题共4题,每小题5分,共计20分。每小题列出的四个选项中有多项
是符合题目要求的,多选或错选不得分)
9.袋子中有2个黑球,1个白球,现从袋子中有放回地随机取球4次,取到白球记0分,黑球记1分,记
4次取球的总分数为 ,则( )
A. B. C.X的期望 D.X的方差
【答案】ACD
【详解】
从袋子中有放回地随机取球4次,则每次取球互不影响,
并且每次取到的黑球概率相等,又取到黑球记1分,
取4次球的总分数,即为取到黑球的个数,
所以随机变量 服从二项分布 ,故A正确;
,记其概率为 ,故B错误;
因为 ,所以 的期望 ,故C正确;
因为 ,所以 的方差 ,故D正确.
故选:ACD.
10.变量x,y之间的一组数据如下表所示:
x 1 3 6 7 8
y 1 2 3 4 5
甲、乙两位同学给出的回归直线方程分别为① 和② ,通过分析得出②的拟合效果更好,则下列分析理由正确的是( )参考公式:
A.①的残差和大于②的残差和,所以②的拟合效果更好
B.①的残差平方和大于②的残差平方和,所以②的拟合效果更好
C.①的 R2小于②的 R2,所以②的拟合效果更好
D.残差图中直线②的残差点分布的水平带状区域比①的残差点分布的水平带状区域更窄,所以②的拟合
效果更好
【答案】BCD
【详解】
解:用 作为拟合直线时,所得 的实际值与 的估计值的差的平方和为:
.
残差和为
用 作为拟合直线时,所得 的实际值与 的估计值的差的平方和为:
.
残差和为
, ①的残差和大于②的残差和,①的残差平方和大于②的残差平方和,则②的拟合效果更好,
故 错误, 正确;
残差图中直线②的残差点分布的水平带状区域比①的残差点分布的水平带状区域更窄,所以直线②拟合效
果更好,故 正确;
,①的 ,②的 ,①的 小于②的 ,②拟合效果更好,故 正确.
故选:BCD.
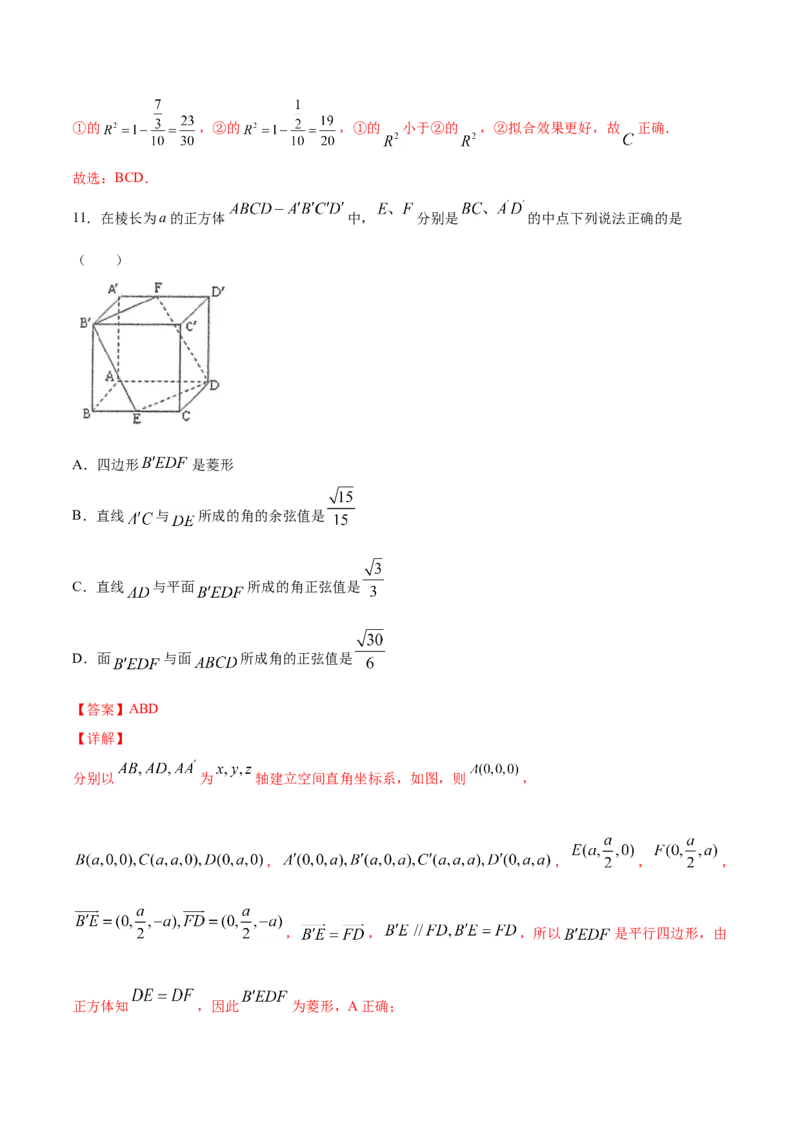
11.在棱长为a的正方体 中, 分别是 的中点下列说法正确的是
( )
A.四边形 是菱形
B.直线 与 所成的角的余弦值是
C.直线 与平面 所成的角正弦值是
D.面 与面 所成角的正弦值是
【答案】ABD
【详解】
分别以 为 轴建立空间直角坐标系,如图,则 ,
, , , ,
, , ,所以 是平行四边形,由
正方体知 ,因此 为菱形,A正确;, ,
,B正确;
,设平面 的一个法向量为 ,
由 得: ,取 ,则 ,即 ,
,
,
直线 与平面 所成的角正弦值是 ,C错;
平面 的一法向量是 ,
,
面 与面 所成角的所以的余弦值为 ,其正弦值为 ,D正确.
故选:ABD.12.已知函数 ,则下列结论正确的是( )
A.若 在 单调递增,则实数
B.当 时, 是 的极值点
C.当 时, 的零点 满足
D.当 时, 恒成立
【答案】AC
【详解】
对于 ,若 在 单调递增,则 在 上恒成立,即 在 上恒
成立,
令 ,则 ,易知函数 在 单调递增,故 (1) ,
,即 ,选项 正确;对于 ,当 时, ,
则 在 上单调递减,在 上单调递增,故 (1) ,
在 上单调递增,无极值点,选项 错误;
对于 ,当 时, , ,
在 上单调递减,在 上单调递增,故 (0) ,
, 在 上递增,则 仅有一个零点 ,
又 ,
由零点存在性定理可知, ,选项 正确;
对于 ,当 时, ,当 时, ,选项 错误.
三、填空题(每小题5分,共计20分)
13.曲线 在点 处的切线方程为___________.
【答案】
【详解】
解: ,则 ,则切线方程为 ,
故答案为: .
14.已知随机变量 服从正态分布 ,若 ,则 ___________.
【答案】
【详解】由题意,随机变量 服从正态分布 ,可得对称轴 ,则 ,
因为 ,
根据正态分布曲线的对称性,可得 .
故答案为: .
15. 展开式中 的系数为__________.
【答案】
【详解】
展开式的通项公式是
,
要求 ,只需 ,解得: .
∴ .
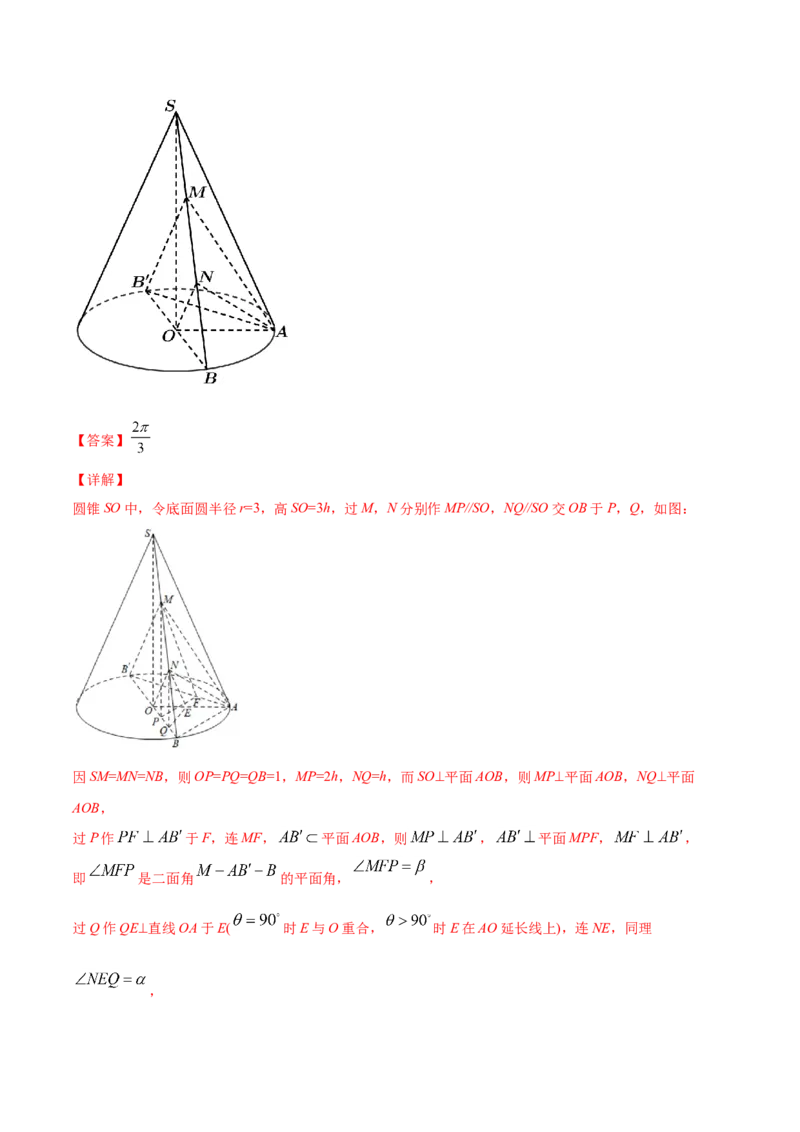
16.如图在圆锥 中,A,B是圆O上的动点, 是圆O的直径,M,N是 的两个三等分点,
,记二面角 , 的平面角分别为 ,若 ,则
的最大值是________.【答案】
【详解】
圆锥SO中,令底面圆半径r=3,高SO=3h,过M,N分别作MP//SO,NQ//SO交OB于P,Q,如图:
因SM=MN=NB,则OP=PQ=QB=1,MP=2h,NQ=h,而SO⊥平面AOB,则MP⊥平面AOB,NQ⊥平面
AOB,
过P作 于F,连MF, 平面AOB,则 , 平面MPF, ,
即 是二面角 的平面角, ,
过Q作QE⊥直线OA于E( 时E与O重合, 时E在AO延长线上),连NE,同理
,因 ,则 , ,
,
与 中, , ,
显然 均为锐角, , ,
即 ,
则 , ,
所以,符合条件的 的最大值是 .
四、解答题(解答题需写出必要的解题过程或文字说明,17题10分,其余各题每题各12
分)
17.某单位为丰富员工的业余生活,利用周末开展趣味野外拉练,此次拉练共分 , , 三大类,其中
类有 个项目,每项需花费 小时, 类有 个项目,每项需花费 小时, 类有 个项目,每项需花
费 小时.要求每位员工从中选择 个项目,每个项目的选择机会均等.
(1)求小张在三类中各选 个项目的概率;
(2)设小张所选 个项目花费的总时间为 小时,求 的分布列.
【答案】(1) ;(2)答案见解析.
【详解】
解:(1)记事件 为在三类中各选 个项目则 ,
所以小张在三类中各选 个项目的概率为 .
(2) 的可能取值为 , , , , , ,则
;
;
;
;
;
.
所以分布列如下表所示:
18.作为世界最大棉花消费国、第二大棉花生产国,我国2020—2021年度棉花产量约 万吨,总需求量
约 万吨,年度缺口约 万吨.其中,新疆棉花产量 万吨,占国内产量比重约 ,占国内消费
比重约 .新疆地区的棉花是世界上最好的棉花之一,新疆长绒棉,世界顶级,做衣被暖和、透气、舒适,长年供不应求.评价棉花质量的重要指标之一就是棉花的纤维长度,新疆农科所在土壤环境不同的
、 两块实验地分别种植某品种的棉花,为了评价该品种的棉花质量,在棉花成熟后,分别从 、 两
地的棉花中各随机抽取 根棉花纤维进行统计,结果如下表:(记纤维长度不低于 的为“长纤
维”,其余为“短纤维”).
纤维长度
地(根数)
地(根数)
(1)由以上统计数据,填写下面 列联表;
(2)判断能否在犯错误概率不超过 的前提下认为“纤维长度与土壤环境有关系”.
地 地 总计
长纤维
短纤维
总计
附:临界值表:
( )
【详解】
(1)根据已知数据得到如下 列联表:
地 地 总计
长纤维
短纤维
总计(2)根据 列联表中的数据,可得 , ,能认为在
犯错误概率不超过 前提下纤维长度与土壤环境有关系.
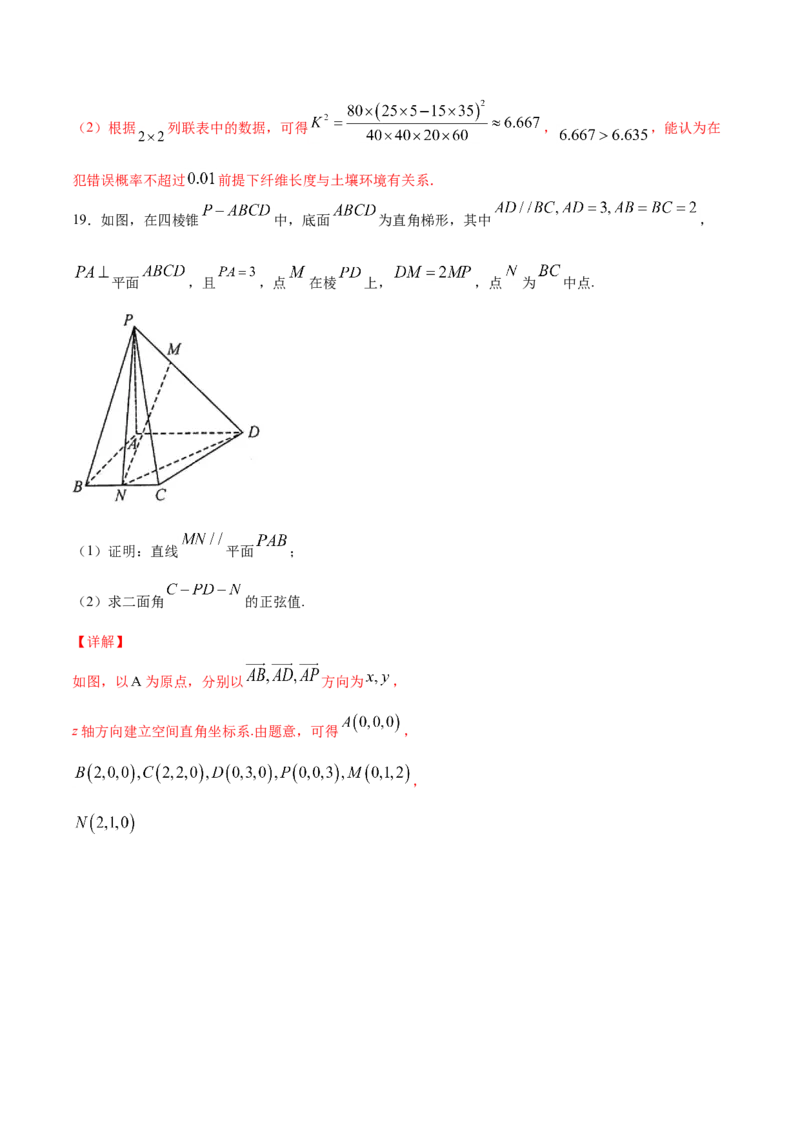
19.如图,在四棱锥 中,底面 为直角梯形,其中 ,
平面 ,且 ,点 在棱 上, ,点 为 中点.
(1)证明:直线 平面 ;
(2)求二面角 的正弦值.
【详解】
如图,以 为原点,分别以 方向为 ,
z轴方向建立空间直角坐标系.由题意,可得 ,
,(1)显然, 是平面 的一个法向量,
,故 ,即 .
又因为 平面 ,
故直线 //平面 .
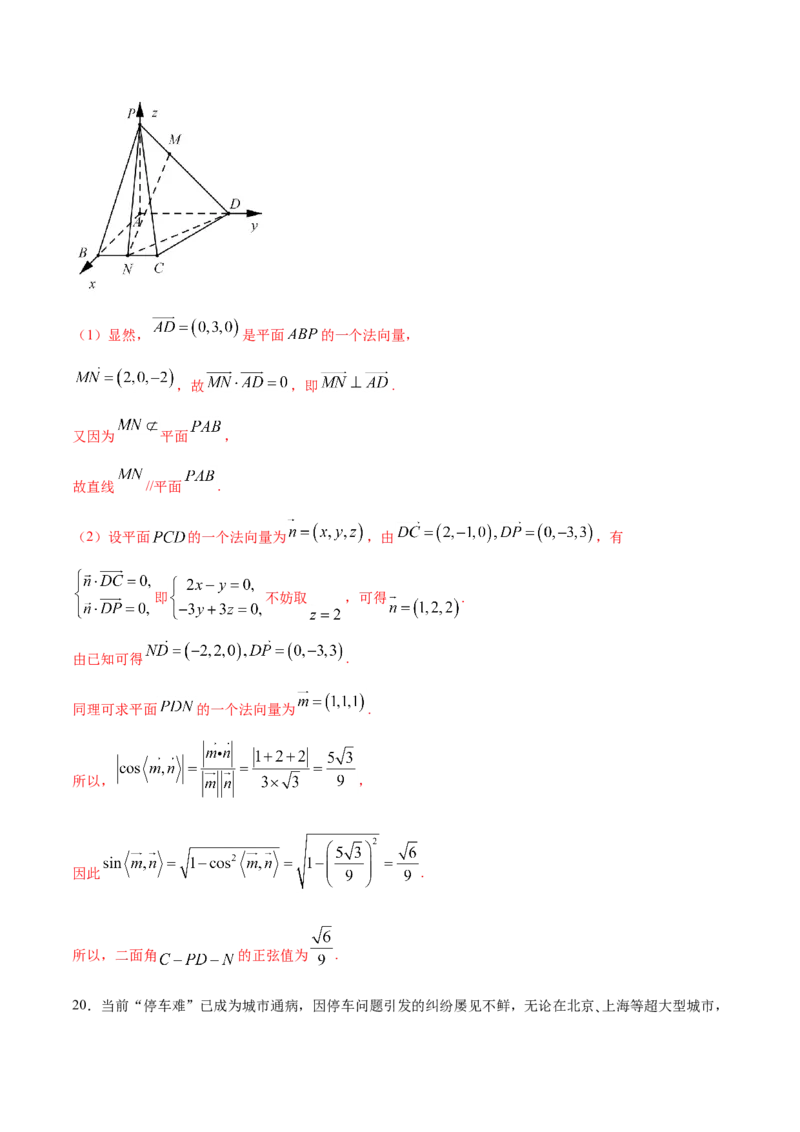
(2)设平面 的一个法向量为 ,由 ,有
即 不妨取 ,可得 .
由已知可得 .
同理可求平面 的一个法向量为 .
所以, ,
因此 .
所以,二面角 的正弦值为 .
20.当前“停车难”已成为城市通病,因停车问题引发的纠纷屡见不鲜,无论在北京、上海等超大型城市,还是其它城市,甚至人口只有几万、十几万的县城和乡镇,“停车难”都给群众生活和政府管理带来了深
深的烦恼,由于“停车难”是事关百姓生活质量和切身利益的问题,也是建设和谐社会不容忽视的问题之
一,某小区物业公司决定动手解决小区“停车难”问题,并统计了近六年小区私家车的数量,以编号1对
应2015年,编号2对应2016年,编号3对应2017年,以此类推,得到相应数据如下:
年份编号 1 2 3 4 5 6
数量
41 96 116 190 218 275
(辆)
(1)若该小区私家车的数量 与年份编号 的关系可用线性回归模型来拟合,试用相关指数 分析其拟
合效果( 精确到 );
(2)由于车辆增加,原有停车位已经不能满足有车业主的需求,因此物业公司欲在小区内对原有停车位
进行改造,重新规划停车位.若要求在2021年小区停车位数量仍可满足需要,求至少需要规划多少个停车
位.
参考数据: , , , .
附:回归方程中斜率和截距的最小二乘法估计公式分别为: , ;
相关指数 ,残差 .
【详解】
(1)由题意得 , ,
∴ ,且 ,
所以 关于 的线性回归方程为 ;
又 时, ; 时, ; 时, ;
时, ; 时, ; 时, ;
故 , ,
由相关指数 近似为 ,接近1,说明拟合效果较好.
(2)在(1)中求得的线性回归方程中,取 ,可得 .
故若要求在2021年小区停车位数量仍可满足需要,则至少需要规划317个停车位.
21.某学校组织一次“强基提素”的知识竞赛,每个参赛选手依次回答 道题,每答对一道获得相应的分
值,再继续答下一道,且在答前 题时,有且仅有一次“复活”机会.即选手首次答错后,裁判会给选手另
外出一道复活题,若选手把复活题答对,则该选手复活成功,接着答下一道题,若选手把复活题答错,则
结束答题,答第 题时没有“复活”机会.每道题的分值如下:
题号 复活题
分值
现有甲、乙两名参赛选手,甲答对每一题(包括复活题)的概率均为 ,乙答对第 、 题的概率均为 ,
答对第 、 、 题的概率均为 ,答对复活题的概率为 ,且两人回答每道题是相互独立的.
(Ⅰ)求甲恰好回答 道题的概率;(Ⅱ)求甲、乙两人的得分之和为 分的概率;
(Ⅲ)求乙的得分不小于 分的概率.
【详解】
(Ⅰ)甲恰好回答 道题分三种情况:①甲连续答对前 道题;②前 题答对,第 题和复活题连续答错;
③前 题中答错 次,复活题答对,第 题答错.
故所求概率为 .
(Ⅱ)两人得分之和为 分仅当两人各得 分.
一名选手得 分有两种情况:①前 题答对第 题和复活题答错;②前 题答对,第 题答错,复活题答
对,第 题答错.
甲得 分的概率为 ;
乙得 分的概率为 .
所以甲、乙两人得分之和为 分的概率为 .
(Ⅲ)设乙的得分为 ,则 小于 分的情况有四种: , , , .
,
,
,,
因此 .
22.已知函数 .
(1)当 时,求曲线 在点 处的切线方程;
(2)讨论 的单调性.
【详解】
解:(1) 时,函数 , ,
则 ,所以 ,
所以曲线 在点 处的切线方程为 ,
.
(2) 的定义域为 ,
①当 时, ,令 ,解得 ;令 ,解得 .
所以 在 上单调递减,在 上单调递增.
②当 时,令 ,解得 或 ;令 ,解得 .
所以 在 , 上单调递增,在 上单调递减.③当 时, ,所以 在 上单调递增.
④当 时,令 ,解得 或 ;令 ,解得 .
所以 在 , 上单调递增,在 上单调递减
综上,当 时, 在 上单调递减,在 上单调递增;当 时, 在 ,
上单调递增,在 上单调递减;当 时, 在 上单调递增;当 时,
在 , 上单调递增,在 上单调递减.