文档内容
普通高中 学年高一质量监测考试
2024-2025
数 学
本试卷满分 分,考试用时 分钟
150 120 .
注意事项:
答题前,先将自己的姓名、准考证号填写在试卷和答题卡上,并将准考证号条形码
1.
粘贴在答题卡上的指定位置
.
选择题的作答:每小题选出答案后,用 铅笔把答题卡上对应题目的答案标号涂
2. 2B
黑 写在试卷、草稿纸和答题卡上的非答题区域均无效
. .
非选择题的作答:用黑色签字笔直接答在答题卡上对应的答题区域内 写在试卷、
3. .
草稿纸和答题卡上的非答题区域均无效
.
考试结束后,请将本试卷和答题卡一并上交
4. .
一、选择题:本题共 小题,每小题 分,共 分.在每小题给出的四个选项中,只有一项
8 5 40
是符合题目要求的.
.若α 则α的终边位于平面直角坐标系第几象限
1 =3rad,
一 二 三 四
A. B. C. D.
.设a b为非零向量 若 a b a b 则
2 , , ( + )·( - )= 0,
a b a b a b a b
A. =- B. = C. · =0 D. =
π
.已知函数f x x θ θ π π 若函数f x 在x 处取得最小值 则θ
3 ( )=cos( + ), ∈(- , ), ( ) = , =
4
π π
3π 3 π
A.- B.- C. D.
4 4 4 4
.学校运动会志愿者服务协会共有 检录组 计分组 宣传组 三个组别 其中 检录
4 “ ”“ ”“ ” , “
组 比 宣传组 多 人 现采用比例分配的分层随机抽样方法从中选出部分志愿者参
” “ ” 8 ,
加田径比赛的志愿服务 如果选出的人中有 人来自 检录组 人来自 计分组
, 3 “ ”,4 “ ”,
人来自 宣传组 那么学校运动会志愿者服务协会 计分组 的人数为
1 “ ”, “ ”
A.16 B.12 C.8 D.4
高一数学试卷 第 页 共 页
1 ( 4 ). ABC中 D为BC的中点 E为AD的中点 则B→E
5 △ , , , =
3A→B 1A→C 3 A→B 1A→C 5 A→B 1A→C 5A→B 1A→C
A.- + B. - C. - D.- +
4 4 4 4 4 4 4 4
. ABC中 A 1 O为 ABC的外心 则 OBC
6 △ ,cos = , △ , sin∠ =
3
2 2 2 1 6
A. B. C. D.
3 3 3 6
.正方体ABCD A B C D 中 AB E是AB的中点 则点A到平面EB D的距离为
7 - 1 1 1 1 , =2, , 1
6 6 6 6
A. B. C. D.
6 4 3 2
B
.锐角 ABC的内角A B C满足 C B B A 则sin 的取值范围为
8 △ , , sin -sin =2sin cos , C
sin
1 1 1
A.(0, ) B.( ,1) C.(0,1) D.( ,1)
2 3 2
二、选择题:本大题共 小题,每小题 分,共计 分,每小题给出的四个选项中,有多项
3 6 18
符合题目要求.全部选对得 分,选对但不全的得部分分,有选错的得 分.
6 0
.若复数z满足 z zz 则z的虚部为
9 ( +1)i= -1,
A.-2 B.-1 C.0 D.1
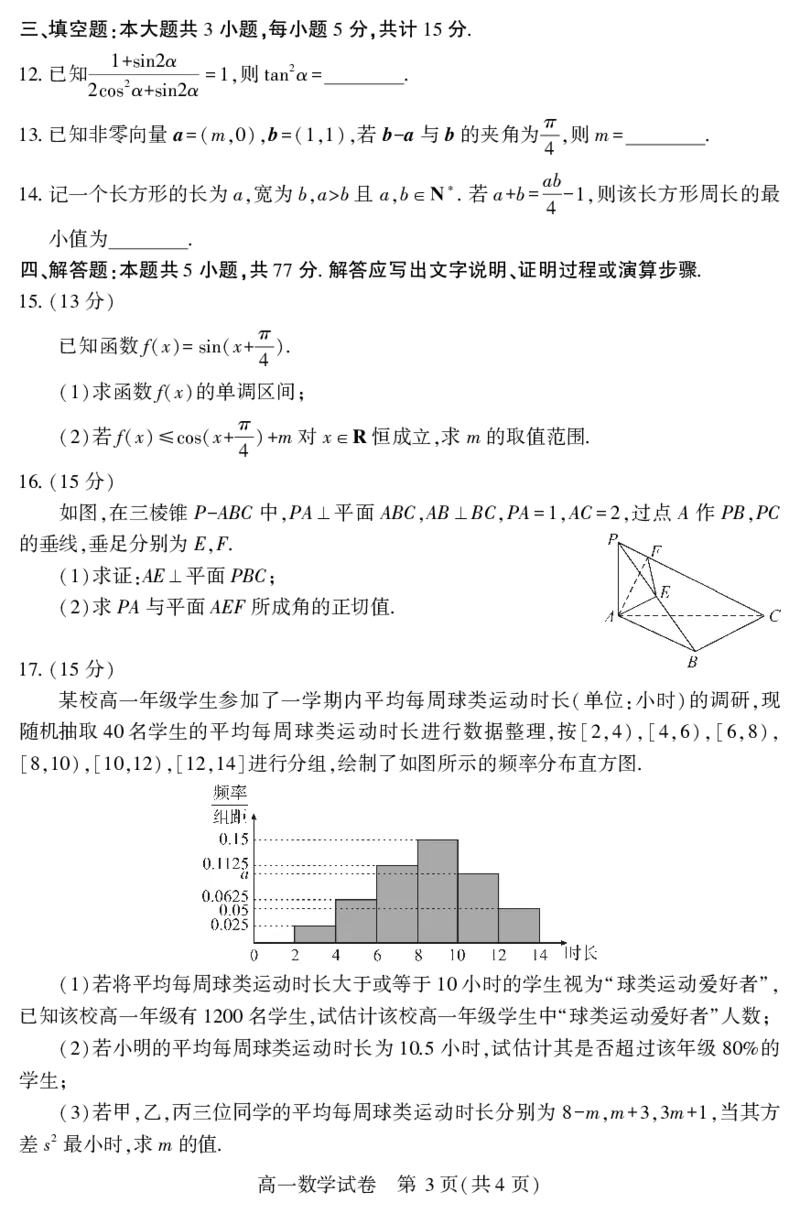
.函数f x ωx φ ω 的部分图象如图所示 则下列说法正确的是
10 ( )=sin( + )( >0) ,
π
f x x
A. ( )=cos(2 - )
3
π
点 11 是函数f x 的图象的一个对称中心
B. (- ,0) ( )
12
π
函数g x x 图象上的所有点的横坐标缩短为
C. ( )=sin( + )
6
原来的1 得到函数f x 的图象
, ( )
2
π
函数f x 的图象向右平移 个单位长度 得到的图象关于y轴对称
D. ( ) ,
3
.已知函数f x sin x -sin x 则下列说法正确的是
11 ( )=e -e ,
π
f x 是偶函数 f x π f x
A. ( + ) B. ( + )= - ( )
2
函数f f x 在 π 内有零点 方程f x 8无解
C. ( ( )) (0, ) D. ( )=
3
高一数学试卷 第 页 共 页
2 ( 4 )三、填空题:本大题共 小题,每小题 分,共计 分.
3 5 15
α
.已知 1+sin2 则 2α .
12 2α α =1, tan =
2cos +sin2
π
.已知非零向量a m b 若b a与b的夹角为 则m .
13 =( ,0), =(1,1), - , =
4
ab
.记一个长方形的长为a 宽为b a b且a b N∗.若 a b 则该长方形周长的最
14 , , > , ∈ + = -1,
4
小值为 .
四、解答题:本题共 小题,共 分.解答应写出文字说明、证明过程或演算步骤.
5 77
. 分
15 (13 )
π
已知函数f x x .
( )=sin( + )
4
求函数f x 的单调区间
(1) ( ) ;
π
若f x x m对x R恒成立 求m的取值范围.
(2) ( )≤cos( + )+ ∈ ,
4
. 分
16 (15 )
如图 在三棱锥P ABC 中 PA 平面 ABC AB BC PA AC 过点 A 作 PB PC
, - , ⊥ , ⊥ , =1, =2, ,
的垂线 垂足分别为E F.
, ,
求证 AE 平面PBC
(1) : ⊥ ;
求PA与平面AEF所成角的正切值.
(2)
. 分
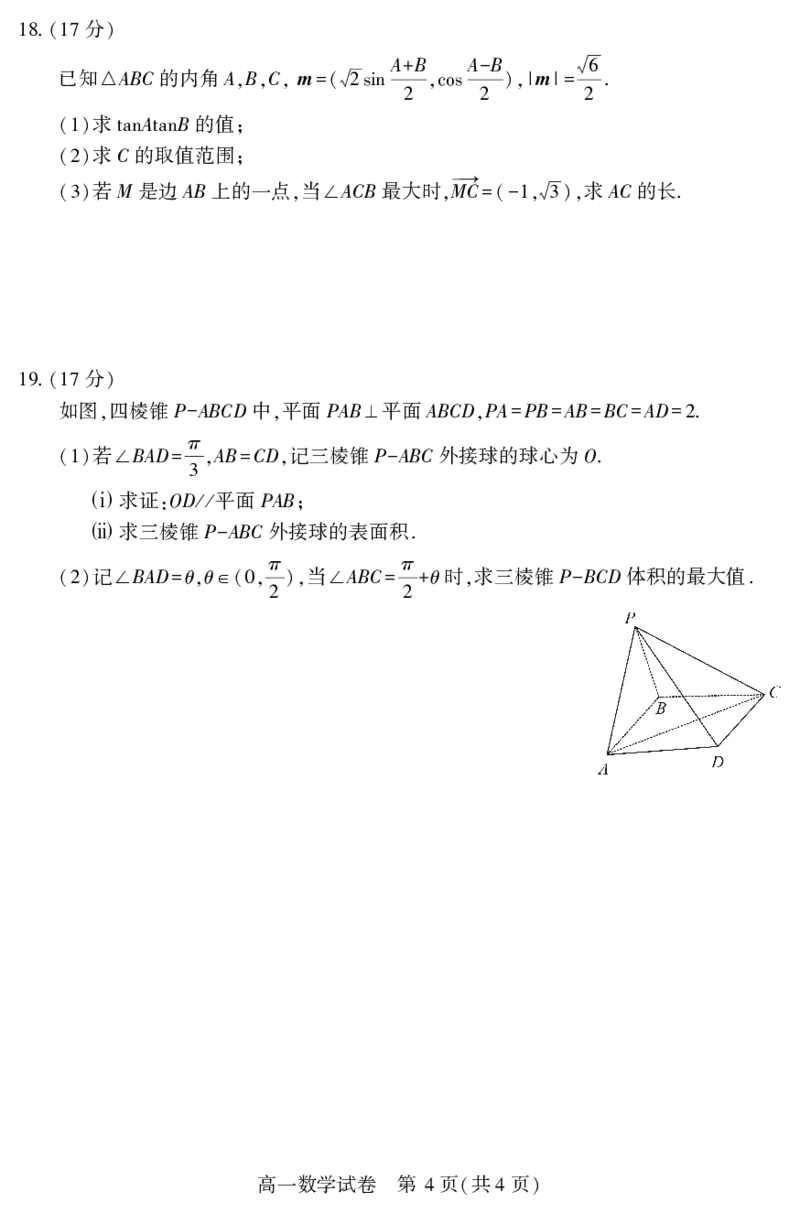
17 (15 )
某校高一年级学生参加了一学期内平均每周球类运动时长 单位 小时 的调研 现
( : ) ,
随机抽取 名学生的平均每周球类运动时长进行数据整理 按
40 , [2,4),[4,6),[6,8),
进行分组 绘制了如图所示的频率分布直方图.
[8,10),[10,12),[12,14] ,
若将平均每周球类运动时长大于或等于 小时的学生视为 球类运动爱好者
(1) 10 “ ”,
已知该校高一年级有 名学生 试估计该校高一年级学生中 球类运动爱好者 人数
1200 , “ ” ;
若小明的平均每周球类运动时长为 . 小时 试估计其是否超过该年级 %的
(2) 10 5 , 80
学生
;
若甲 乙 丙三位同学的平均每周球类运动时长分别为 m m m 当其方
(3) , , 8- , +3,3 +1,
差s2 最小时 求m的值.
,
高一数学试卷 第 页 共 页
3 ( 4 ). 分
18 (17 )
A B A B
已知 ABC的内角A B C m + - m 6 .
△ , , , =( 2sin ,cos ),| |=
2 2 2
求 A B的值
(1) tan tan ;
求C的取值范围
(2) ;
若M是边AB上的一点 当 ACB最大时 M→C 求AC的长.
(3) , ∠ , =(-1, 3),
. 分
19 (17 )
如图 四棱锥P ABCD中 平面PAB 平面ABCD PA PB AB BC AD .
, - , ⊥ , = = = = =2
π
若 BAD AB CD 记三棱锥P ABC外接球的球心为O.
(1) ∠ = , = , -
3
求证 OD/ /平面PAB
: ;
求三棱锥P ABC外接球的表面积.
-
π π
记 BAD θ θ 当 ABC θ时 求三棱锥P BCD体积的最大值.
(2) ∠ = , ∈(0, ), ∠ = + , -
2 2
高一数学试卷 第 页 共 页
4 ( 4 )