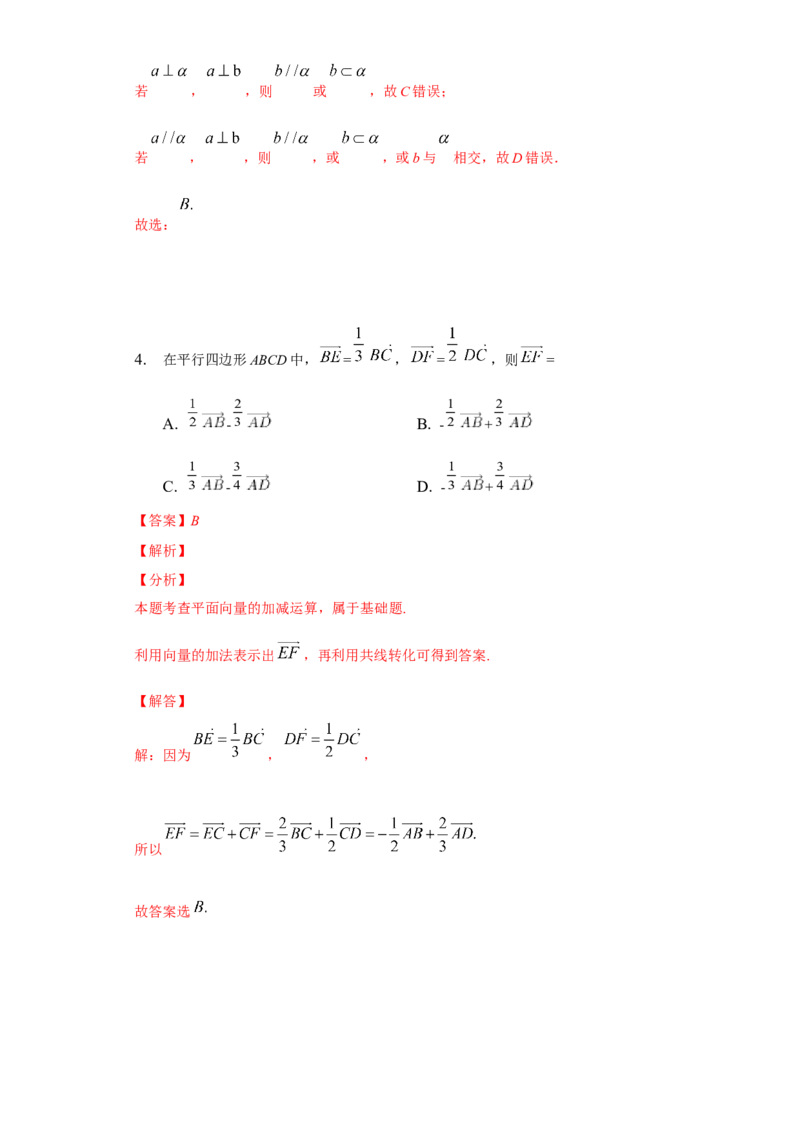文档内容
期末模拟试卷 1
一、单项选择题
1. 若复数 的虚部为1,则 在复平面对应的点的坐标为
A. B. C. D.
【答案】A
【解析】
【分析】
本题考察复数的概念,共轭复数和复数的几何意义,属于基础题.
根据虚部为1求出m,再根据共轭复数定义写出答案.
【解答】
解: 的虚部为1,
得 ,所以 , ,
故 在复平面对应的点的坐标为 ,
故答案选
2. “幸福感指数”是指某个人主观地评价他对自己目前生活状态的满意程度的指标,
常用区间 内的一个数来表示,该数越接近10表示满意程度越高,现随机抽
取6位小区居号,他们的幸福感指数分别为5,6,7,8,9,5,则这组数据的第
80百分位数是
A. 7 B. C. 8 D. 9【答案】C
【解析】
【分析】
本题考查一组数据的百分数问题,属于基础题.
把该组数据从小到大排列,计算 ,从而找出对应的第80百分位数;
【解答】
解:该组数据从小到大排列为:5,5,6,7,8,9,且 ,
故选:
3. 设 为平面,a,b为两条不同的直线,则下列叙述正确的是
A. 若 , ,则 B. 若 , ,则
C. 若 , ,则 D. 若 , ,则
【答案】B
【解析】
【分析】
本题考查命题的真假的判断,是基础题,解题时要认真审题,注意空间思维能力的培
养.
利用空间线线、线面、面面间的关系对每一个选项逐一分析判断得解.
【解答】
解:若 , ,则a与b相交、平行或异面,故A错误;
若 , ,则由直线与平面垂直的判定定理知 ,故B正确;若 , ,则 或 ,故C错误;
若 , ,则 ,或 ,或b与 相交,故D错误.
故选:
4. 在平行四边形ABCD中, = , = ,则 =
2 1 2
A. -3 B. -2 +3
1 3 1 3
C. 3 -4 D. -3 +4
【答案】B
【解析】
【分析】
本题考查平面向量的加减运算,属于基础题.
利用向量的加法表示出 ,再利用共线转化可得到答案.
【解答】
解:因为 , ,
所以
故答案选5. 已知圆锥的表面积为 ,且它的侧面展开图是一个半圆,则该圆锥的体积为
A. B. C. D.
【答案】A
【解析】
【分析】
本题主要考查圆的面积、周长、圆锥的侧面积及体积等知识点,考查运算求解能力,
属于基础题型.
设圆锥的底面半径为r,高为h,母线为l,根据其表面积为 ,得到 ,再
由它的侧面展开图是一个半圆,得到 ,联立求得半径和高,利用体积公式求
解.
【解答】
解:设圆锥的底面半径为r,高为h,母线为l,
因为其表面积为 ,
所以 ,
即 ,
又因为它的侧面展开图是一个半圆,
所以 ,
即 ,所以 ,
所以此圆锥的体积为
故选:
6. 《史记》中讲述了田忌与齐王赛马的故事,其中,田忌的上等马优于齐王的中等
马,劣于齐王的上等马;田忌的中等马优于齐王的下等马,劣于齐王的中等马;
田忌的下等马劣于齐王的下等马,若双方各自拥有上等马、中等马、下等马各1
匹,且双方各自随机选1匹马进行1场比赛,则田忌的马获胜的概率为
A. B. C. D.
【答案】C
【解析】
【分析】
本题考查古典概型,是基础题.
本题先将所有的基本事件都列出来共9种,再将田忌的马获胜的事件选出共3种,最
后计算概率即可.
【解答】
解:设田忌的上等马为 ,中等马为: ,下等马为 ,
齐王的上等马为 ,中等马为: ,下等马为 ,双方各自随机选1匹马进行1场比赛产生的基本事件为:
, , , , , , , , ,共9种;
其中田忌的马获胜的事件为: , , ,共3种,
所以田忌的马获胜的概率为:
故选:
7. 雕塑成了大学环境不可分割的一部分,有些甚至能成为这
个大学的象征,在中国科学技术大学校园中就有一座郭沫
若的雕像.雕像由像体AD和底座CD两部分组成.如图,
在 中, ,在 中,
,且 米,求像体AD的高度 最后结果精确到 米,
参考数据: , ,
A. 米 B. 米 C. 米 D. 米
【答案】B
【解析】
【分析】
本题考查解三角形的实际应用中的高度问题的求解,属于基础题.
在 和 中,利用正切值可求得AC,进而求得【解答】
解:在 中, 米 ,
在 中, 米 ,
米
故选:
8. 如图,在平面直角坐标系xOy中,原点O为正八边形 的中心,
轴,若坐标轴上的点 异于点 满足 其中
,且i、 ,则满足以上条件的点M的个数为
A. 2 B. 4 C. 6 D. 8
【答案】D
【解析】
【分析】
本题考查符合条件的点的个数的求解,考查了平面向量加法法则的应用,属于中等题.分点M在x、y轴进行分类讨论,可得出点 、 关于坐标轴对称,由此可得出点M
的个数.
【解答】
解:分以下两种情况讨论:
①若点M在x轴上,则 、 关于x轴对称,
由图可知, 与 、 与 、 与 、 与 关于x轴对称,
此时,符合条件的点M有4个;
②若点M在y轴上,则 、 关于y轴对称,
由图可知, 与 、 与 、 与 、 与 关于y轴对称,
此时,符合条件的点M有4个.
综上所述,满足题中条件的点M的个数为
故选:
二、多项选择题
9. 已知复数z满足 ,则下列关于复数z的结论正确的是
A.
B. 复数z的共轭复数为C. 复平面内表示复数z的点位于第二象限
D. 复数z是方程 的一个根
【答案】ABCD
【解析】
【分析】
本题考查了复数的除法运算,考查了复数的模长公式,考查了复数的几何意义,属于
基础题.
利用复数的除法运算求出 ,再根据复数的模长公式求出 ,可知A正确;
根据共轭复数的概念求出 ,可知B正确;根据复数的几何意义可知C正确;将z代
入方程成立,可知D正确.
【解答】
解:因为 ,所以 ,所以
,故A正确;
所以 ,故B正确;
由 知,复数z对应的点为 ,它在第二象限,故C正确;
因为 ,所以D正确.
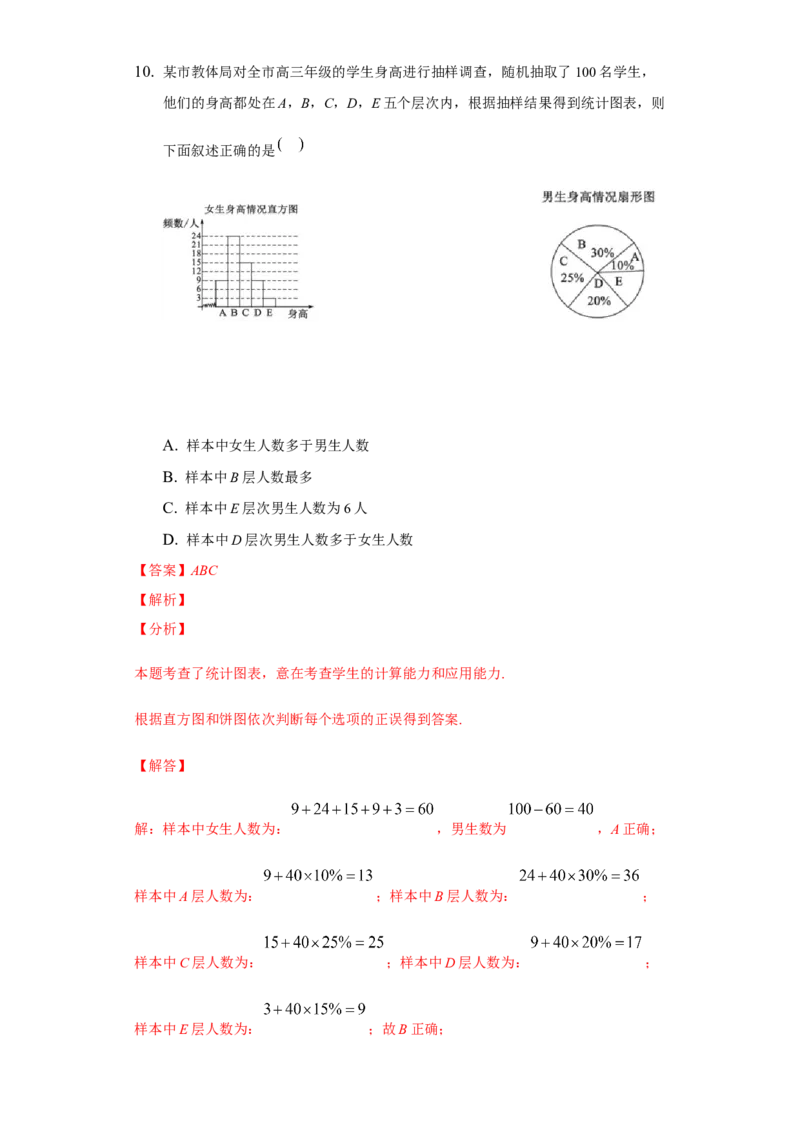
故选:10. 某市教体局对全市高三年级的学生身高进行抽样调查,随机抽取了100名学生,
他们的身高都处在A,B,C,D,E五个层次内,根据抽样结果得到统计图表,则
下面叙述正确的是
A. 样本中女生人数多于男生人数
B. 样本中B层人数最多
C. 样本中E层次男生人数为6人
D. 样本中D层次男生人数多于女生人数
【答案】ABC
【解析】
【分析】
本题考查了统计图表,意在考查学生的计算能力和应用能力.
根据直方图和饼图依次判断每个选项的正误得到答案.
【解答】
解:样本中女生人数为: ,男生数为 ,A正确;
样本中A层人数为: ;样本中B层人数为: ;
样本中C层人数为: ;样本中D层人数为: ;
样本中E层人数为: ;故B正确;样本中E层次男生人数为: ,C正确;
样本中D层次男生人数为: ,女生人数为9,D错误.
故选:
11. 已知事件A,B,且 , ,则下列结论正确的是
A. 如果 ,那么 ,
B. 如果A与B互斥,那么 ,
C. 如果A与B相互独立,那么 ,
D. 如果A与B相互独立,那么 ,
【答案】BD
【解析】
【分析】
本题考查在包含关系,互斥关系,相互独立的前提下的和事件与积事件的概率,是基
础题.
A选项在 前提下,计算出 , ,即可判断;
B选项在A与B互斥前提下,计算出 , ,即可判断;C、D选项在A与B相互独立前提下,计算出 , ,
, ,即可判断.
【解答】
解:A选项:如果 ,那么 , ,故A选项错误;
B选项:如果A与B互斥,那么 , ,故B选项正确;
C选项:如果A与B相互独立,那么 , ,故C选项错误;
D选项:如果A与B相互独立,那么 ,
,故D选项正确.
故选:
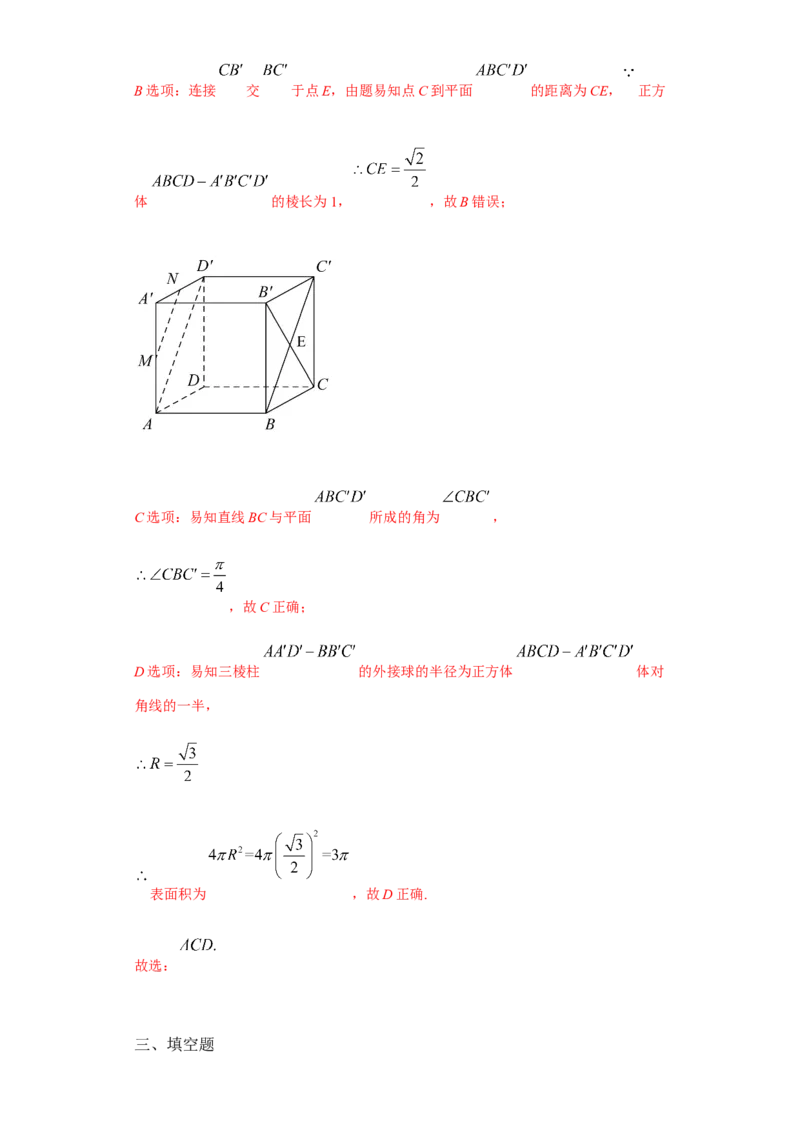
12. 如图,正方体 的棱长为1,则下
列四个命题正确的是
A. 若点M,N分别是线段 , 的中点,则B. 点C到平面 的距离为
C. 直线BC与平面 所成的角等于
D. 三棱柱 的外接球的表面积为
【答案】ACD
【解析】
【分析】
本题考查命题真假的判断,通过线线平行、点到面的距离、线面角,以及外接球的知
识点来考查,解题时要注意空间思维能力的培养,是中档题.
A选项:通过平行的传递性得到结论;
B选项:根据点C到平面 的距离为CE,进一步得到答案;
C选项:根据直线BC与平面 所成的角为 ,进一步得出结论;
D选项:根据三棱柱 的外接球的半径为正方体 体对
角线的一半,进一步得到答案.
【解答】
解:A选项:若点M,N分别是线段 , 的中点,则 又
所以 ,故A正确;B选项:连接 交 于点E,由题易知点C到平面 的距离为CE, 正方
体 的棱长为1, ,故B错误;
C选项:易知直线BC与平面 所成的角为 ,
,故C正确;
D选项:易知三棱柱 的外接球的半径为正方体 体对
角线的一半,
表面积为 ,故D正确.
故选:
三、填空题13. 已知a,b,c分别为 三个内角A,B,C的对边,且
,则 __________.
【答案】
【解析】
【分析】
本题主要考查正弦定理的应用.解题的关键是利用正弦定理把等式中的边转化为角的
正弦,属于基础题.
根据正弦定理把已知等式中的边转化为角的正弦,利用两角和公式化简求得 的值
进而求得
【解答】
解: ,
,
,
,
由于A为三角形内角,可得
故答案为:14. 已知数据 , , ,…, 的平均数为10,方差为2,则数据 ,
, ,…, 的平均数为__________,方差为__________.
【答案】19
8
【解析】
【分析】
本题考查了平均数与方差的计算,考查了运算求解能力,属于基础题.
由题意结合平均数公式和方差公式计算即可得解.
【解答】
解:由已知条件可得 ,
,
所以数据 、 、 、 、 的平均数为
,
方差为,
故答案为:19;
15. 已知 , , ,则 与 的夹角为__________.
【答案】
【解析】
【分析】
本题考查运用向量数量积的定义与运算求向量的夹角,是基础题.
先求 , , ,再根据 化简整
理得 ,最后求 与 的夹角为
【解答】
解: , ,, ,
,
,
,
整理得: ,
与 的夹角为:
故答案为:
16. 如图,在三棱锥 中, , , ,且 ,
,则二面角 的余弦值是__________.【答案】
【解析】
【分析】
本题考查二面角余弦值的计算,考查二面角的定义,考查计算能力,属于中等题.
取AB的中点O,连接VO、OC,证明出 , ,可得出二面角
的平面角为 ,计算出VO、OC,利用余弦定理求得 ,
由此可得出二面角 的余弦值.
【解答】
解:取AB的中点O,连接VO、OC,如下图所示:
,O为AB的中点,则 ,且 , ,
,
同理可得 ,且 ,所以,二面角 的平面角为 ,由余弦定理得 ,
因此,二面角 的余弦值为
故答案为:
四、解答题
17. 已知向量 ,
求向量 与 的夹角;
若 ,且 ,求m的值
【答案】解: , ,
,
由题得 , ,
设向量 与 的夹角为 ,则 ,,所以 ,
即向量 与 的夹角为
, , ,
, ,
, ,解得
【解析】本题考查了向量的夹角公式,向量的坐标运算和向量的垂直的条件,属于中
档题.
根据向量的坐标运算和向量的夹角公式即可求出.
根据向量的坐标运算先求出 ,再由垂直的条件得到
,解得即可.
18. 已知a、b、c分别为 三个内角A、B、C的对边,且 , ,
求b及 的面积S;
若D为BC边上一点,且,______,求 的正弦值.从① ,② 这两个条件中任选一个,补充在上面问题中,并作
答.
【答案】解: 由余弦定理得 ,
整理得 ,
,
,
;
选①,如下图所示:
在 中,由正弦定理得 ,
可得 ,在 中, ,则 ,
;
选②,在 中,由正弦定理得 ,
可得 ,
由于 为锐角,则 ,
,
【解析】本题考查利用正、余弦定理解三角形以及三角形面积的计算,同时也考查了
三角恒等变换,考查计算能力,属于中档题.利用余弦定理可得出关于b的二次方程,可解出b的值,进而可求得 的面积
S;
选①,在 中,利用正弦定理可求得 的值,再由 可得出
,进而可求得 的正弦值;
选②,利用正弦定理求得 的值,由同角三角函数的基本关系可求得 ,
再利用两角和的正弦公式可求得 的值.
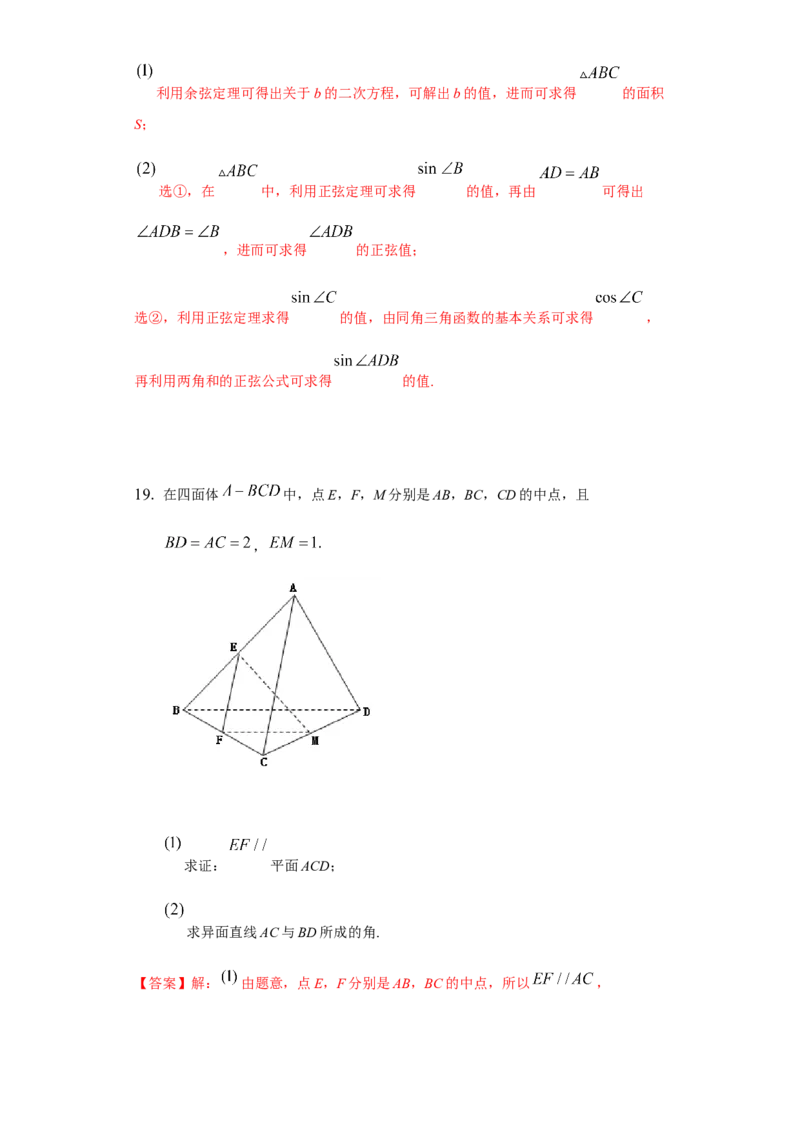
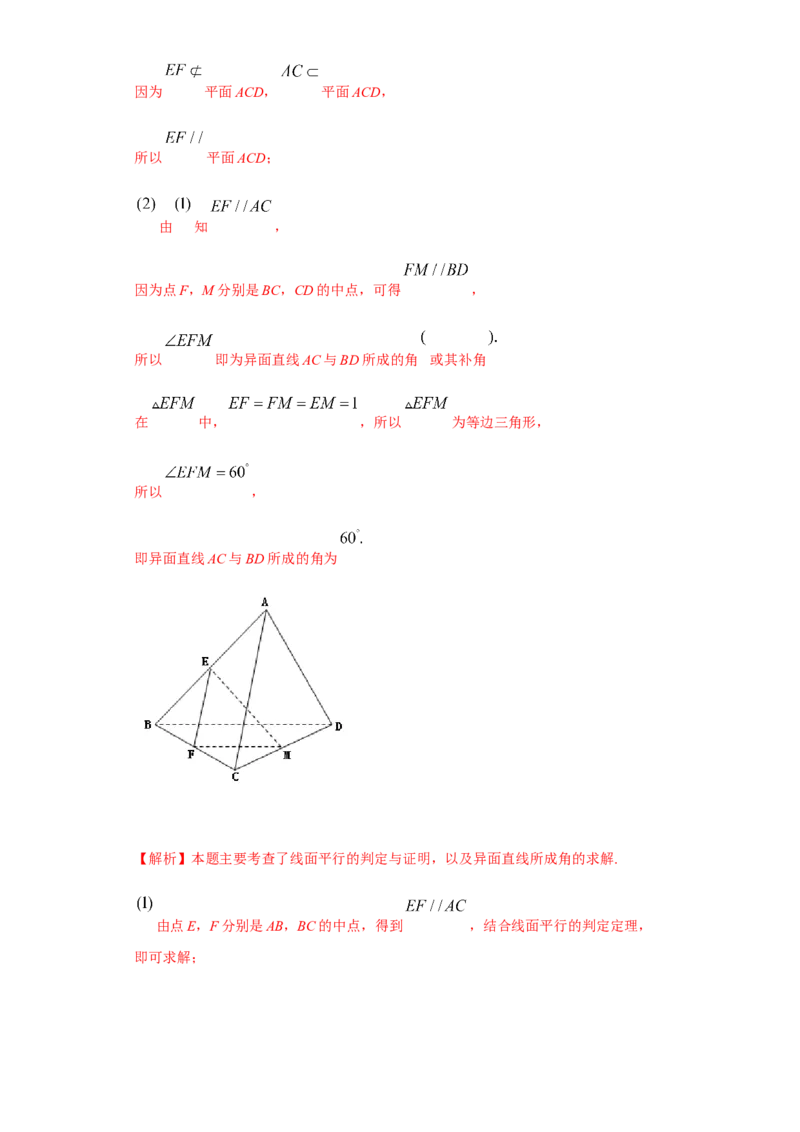
19. 在四面体 中,点E,F,M分别是AB,BC,CD的中点,且
,
求证: 平面ACD;
求异面直线AC与BD所成的角.
【答案】解: 由题意,点E,F分别是AB,BC的中点,所以 ,因为 平面ACD, 平面ACD,
所以 平面ACD;
由 知 ,
因为点F,M分别是BC,CD的中点,可得 ,
所以 即为异面直线AC与BD所成的角 或其补角
在 中, ,所以 为等边三角形,
所以 ,
即异面直线AC与BD所成的角为
【解析】本题主要考查了线面平行的判定与证明,以及异面直线所成角的求解.
由点E,F分别是AB,BC的中点,得到 ,结合线面平行的判定定理,
即可求解;由 知 和 ,得到 即为异面直线AC与BD所成的角,
在 中,即可求解.
20. 溺水、校园欺凌等与学生安全有关的问题越来越受到社会的关注和重视,为了普
及安全教育,某市组织了一次学生安全知识竞赛,规定每队3人,每人回答一个
问题,答对得1分,答错得0分.在竞赛中,甲、乙两个中学代表队狭路相逢,
假设甲队每人回答问题正确的概率均为 ,乙队每人回答问题正确的概率分别为
,且两队各人回答问题正确与否相互之间没有影响.
分别求甲队总得分为3分与1分的概率;
求甲队总得分为2分且乙队总得分为1分的概率.
【答案】解: 记“甲队总得分为3分”为事件A,记“甲队总得分为1分”为事件
B,
甲队得3分,即三人都回答正确,其概率为 ,
甲队得1分,即三人中只有1人回答正确,其余两人都答错,
其概率为
甲队总得分为3分与1分的概率分别为 ,记“甲队得分为2分”为事件C,记“乙队得分为1分”为事件D,
事件C即甲队三人中有2人答对,其余1人答错,
则 ,
事件D即乙队3人中只有1人答对,其余2人答错,
则 ,
由题意得事件C与事件D相互独立,
甲队总得分为2分且乙队总得分为1分的概率:
【解析】本题考查概率的求法,考查相互独立事件概率乘法公式等基础知识,考查运
算求解能力,属于中档题.
记“甲队总得分为3分”为事件A,记“甲队总得分为1分”为事件B,甲队得3
分,即三人都回答正确,甲队得1分,即三人中只有1人回答正确,其余两人都答错,
由此利用相互独立事件概率乘法公式能求出甲队总得分为3分与1分的概率.
记“甲队得分为2分”为事件C,记“乙队得分为1分”为事件D,事件C即甲队
三人中有2人答对,其余1人答错,事件D即乙队3人中只有1人答对,其余2人答错,
由题意得事件C与事件D相互独立,由此利用相互独立事件概率乘法公式能求出甲队
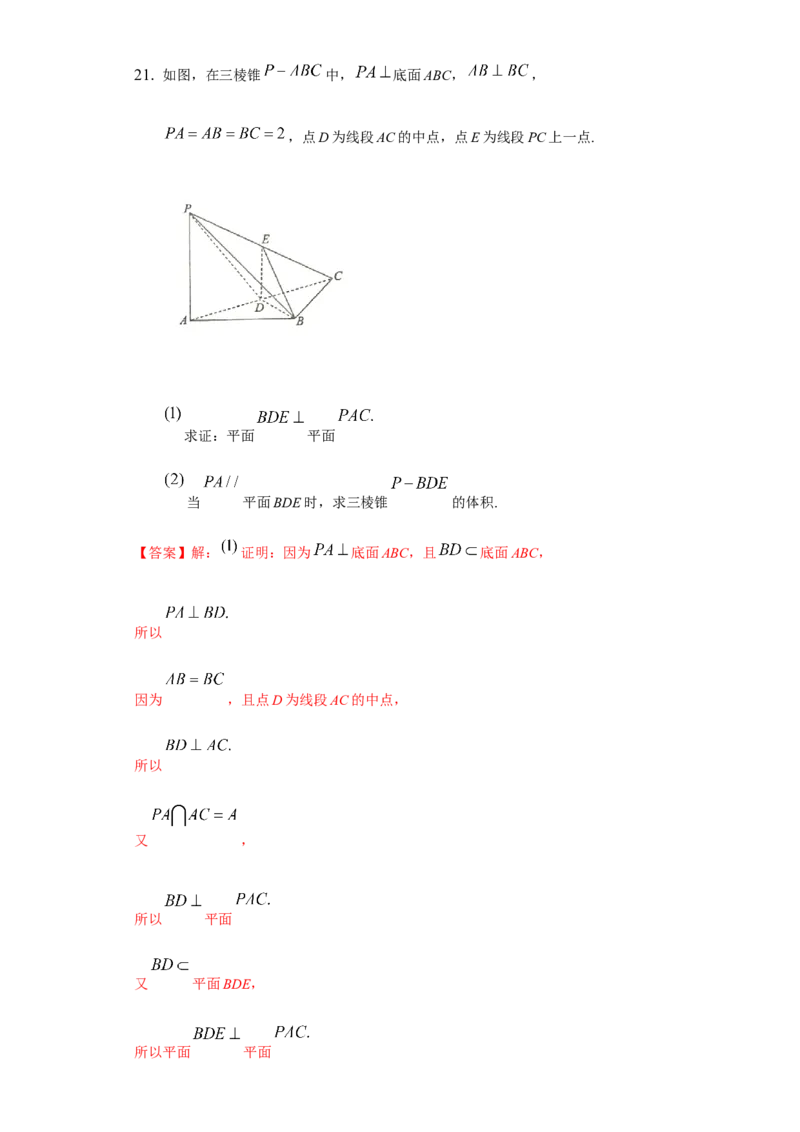
总得分为2分且乙队总得分为1分的概率.21. 如图,在三棱锥 中, 底面ABC, ,
,点D为线段AC的中点,点E为线段PC上一点.
求证:平面 平面
当 平面BDE时,求三棱锥 的体积.
【答案】解: 证明:因为 底面ABC,且 底面ABC,
所以
因为 ,且点D为线段AC的中点,
所以
又 ,
所以 平面
又 平面BDE,
所以平面 平面解:因为 平面BDE, 平面PAC,平面 平面 ,
所以
因为点D为AC的中点,所以点E为PC的中点.
法一:
由题意知点P到平面BDE的距离与点A到平面BDE的距离相等,
所以
所以三棱锥 的体积为
法二:
因为 平面BDE,
由题意知点P到平面BDE的距离与点A到平面BDE的距离相等.
所以 ,又 , , , ,
由 知, ,又 ,且 ,所以 平面BDE,
所以
所以三棱锥 的体积为
法三:
又 , , , ,
由 知: 平面PDE,
且
所以
所以三棱锥 的体积为【解析】本题考查面面垂直的证明,三棱锥的体积,是中档题.
先证明 ,再证明 ,从而证明 平面PAC,最后证明平面
平面PAC;
先判断点E为PC的中点,再判断三棱锥 的体积等于三棱锥 的
体积,最后求体积即可.
22. 2020年开始,山东推行全新的高考制度,新高考不再分文理科,采用“ ”模
式,其中语文、数学、外语三科为必考科目,满分各150分,另外考生还需要依
据想考取的高校及专业要求,结合自己的兴趣爱好等因素,在思想政治、历史、
地理、物理、化学、生物6门科目中自选3门参加考试 选 ,每科满分100分,
2020年初受疫情影响,全国各地推迟开学,开展线上教学.为了了解高一学生的
选科意向,某学校对学生所选科目进行线上检测,下面是100名学生的物理、化
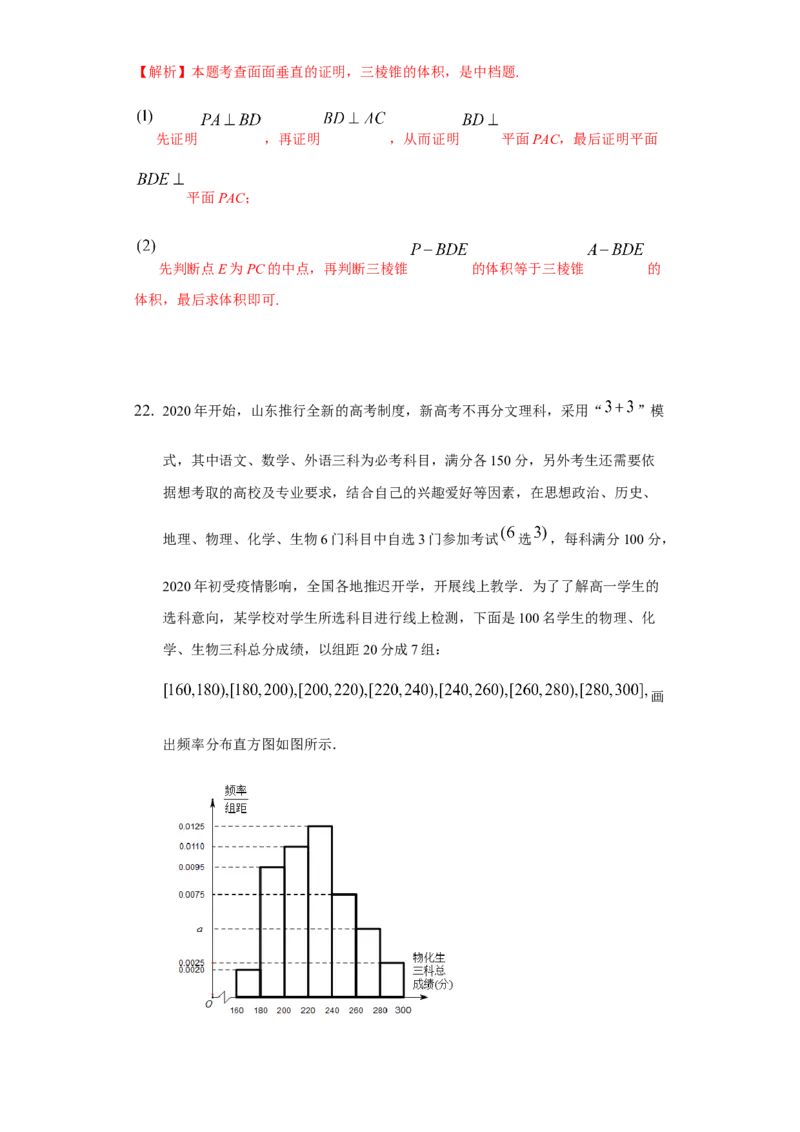
学、生物三科总分成绩,以组距20分成7组:
画
出频率分布直方图如图所示.求频率分布直方图中a的值;
由频率分布直方图;
求物理、化学、生物三科总分成绩的中位数;
估计这100名学生的物理、化学、生物三科总分成绩的平均数 同一组中的数
据用该组区间的中点值作代表 ;
为了进一步了解选科情况,由频率分布直方图,在物理、化学、生物三科总分
成绩在 和 的两组中,用分层随机抽样的方法抽取7名学生,
再从这7名学生中随机抽取2名学生进行问卷调查,求抽取的这2名学生来自不
同组的概率.
【答案】解: 由 ,
得 ;
因为 ,
,
所以中位数在 设中位数为x,
所以 ,解得 ,
所以物理、化学、生物三科总分成绩的中位数为224;这100名学生的物理、化学、生物三科总分成绩的平均数为
物理、化学、生物三科总分成绩在 和 的两组中的人数分别为:
人, 人,
根据分层随机抽样可知,
从成绩在 的组中应抽取 人,记为 ,
从成绩在 的组中应抽取2人,记为 ,
从这7名学生中随机抽取2名学生的所有基本事件为:
,
,共有21种,
其中这2名学生来自不同组的共有10种,
根据古典概型的概率公式可得所求概率为
【解析】本题考查了利用频率分布直方图求中位数、平均数,考查了分层抽样,考查
了古典概型的概率公式,属于中档题.根据7组频率和为1列方程可解得结果;
根据前三组频率和为 ,前四组频率和为 可知中位数在第四
组,设中位数为x,根据 即可解得结果;
利用各组的频率乘以各组的中点值,再相加即可得解;
根据分层抽样可得从成绩在 的组中应抽取5人,从成绩在 的
组中应抽取2人,再用列举法以及古典概型的概率公式可得解.