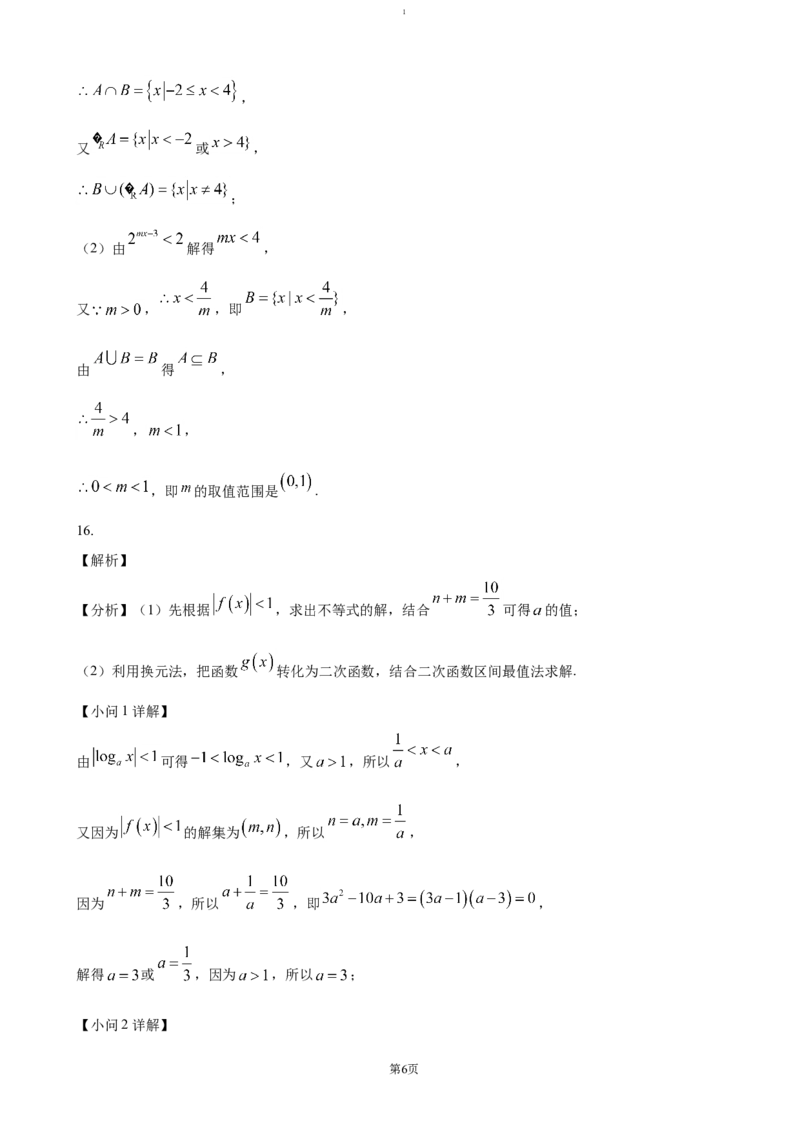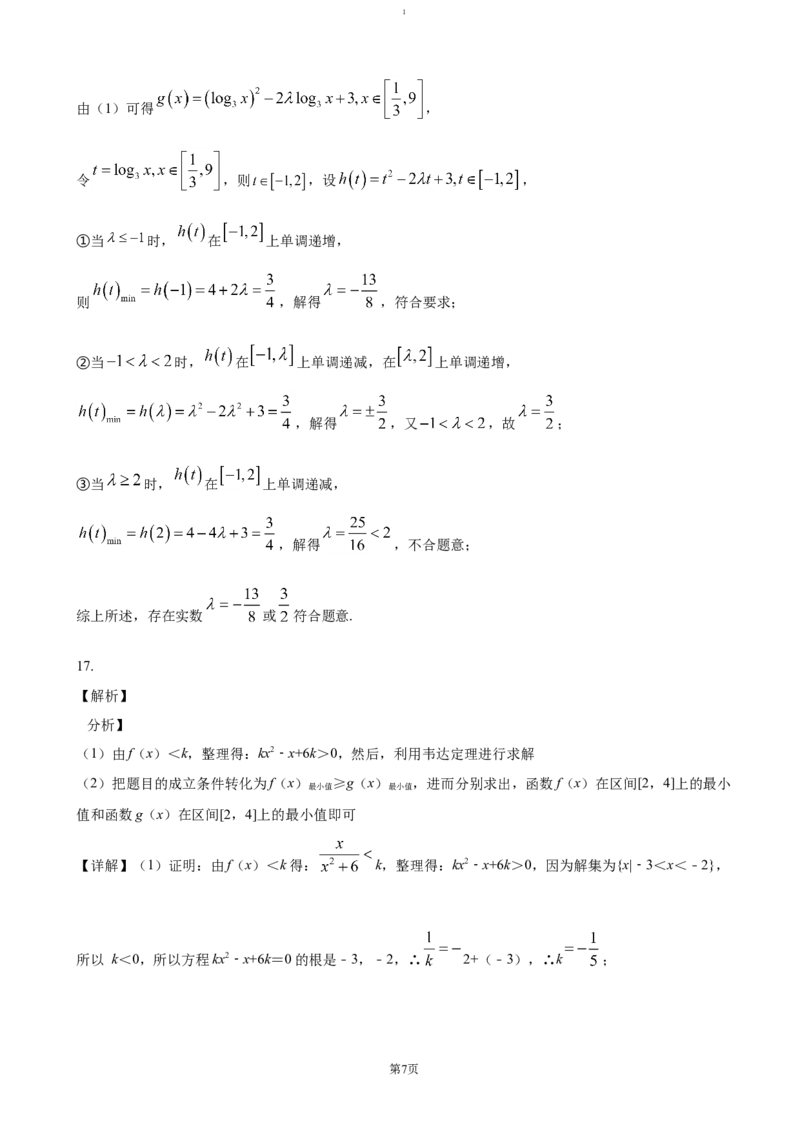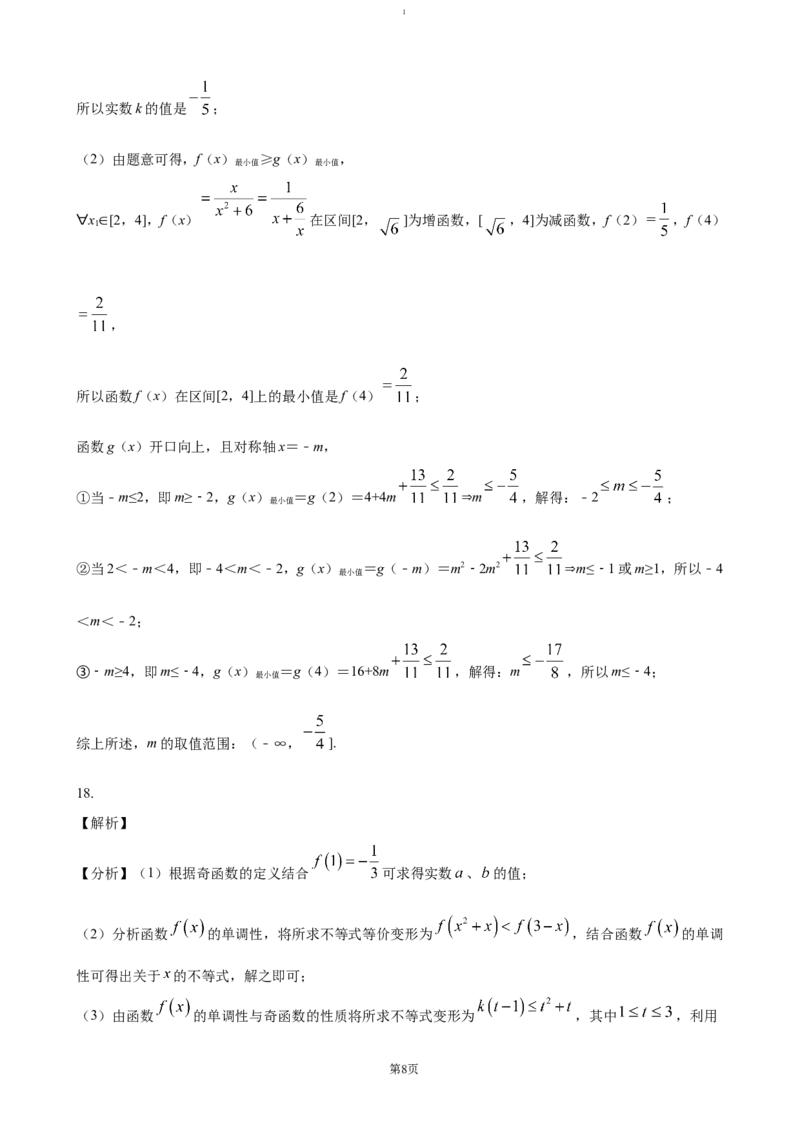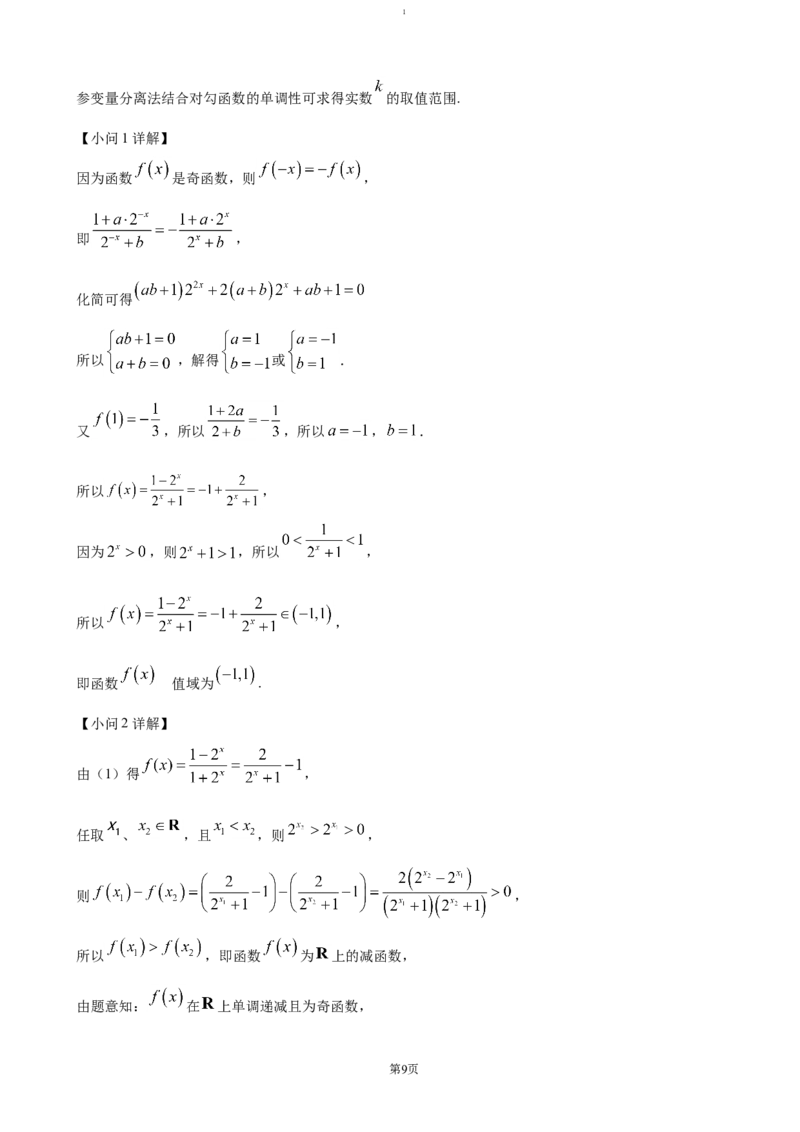文档内容
1
大余县梅关中学 2024-2025 学年度高一上学期第二次月考
数学试卷
一、单选题
1. 已知a, ,且 ,则下列不等关系中正确的是()
A. B. C. D.
2. 已知 ,则下列语句能成为“ 都不小于1”的否定形式的是( )
A. 中至少有1个大于1 B. 都小于1
C. 都不大于1 D. 或 或
3. 已知函数 ,对任意 ,则实数 的取位
范围是()
A. B. C. 或 D.
4. 已知偶函数 的定义域为 , 在 上单调递增,则 , , 的大小关
系是()
A. B.
C. D.
5. 已知函数 ,则 ()
是
A. 奇函数且在 上递减 B. 是奇函数且在 上递增
C. 是偶函数且在 上递减 D. 是偶函数且在 上递增
6. 已知函数 ( ,且 )在区间 上单调递增,则实数 的取值范围为()
第1页1
A. B.
C. D.
7. 设 ,则 的大小关系为()
A. B. C. D.
8. 定义在 上的奇函数 在区间 上单调递减,且 ,则不等式 的解集为(
)
A. B.
C. D.
二、多选题
的
9. 下列结论正确 有()
A. B.
C. D. 若 ,则 .
10. 对于给定 的实数 ,关于实数 的一元二次不等式 的解集可能为()
A. B. C. D.
11. 已知定义在 上的函数 满足 ,且 是奇函数,则()
A. 的图象关于点 对称
B.
C.
第2页1
D. 若 ,则
三、填空题
12. 已知 ,命题“存在 ,使 ”为假命题,则 的取值范围为______.
13. 函数 的单调增区间为______.
14. 已知 ,则 _______.
四、解答题
15. 已知集合 , .
(1)当 时,求 , ;
(2)当 , 时,求实数 的取值范围.
16. 已知函数 ,关于 的不等式 的解集为 ,且 .
(1)求 的值;
(2)是否存在实数 ,使函数 的最小值为 ?若存在,求出
的值;若不存在,说明理由.
17. 已知函数 .
(1)若f(x)<k的解集为{x|﹣3<x<﹣2},求实数k的值;
(2)若∀x
1
∈[2,4],都∃x
2
∈[2,4],使f(x
1
)≥g(x
2
)成立,求实数m的取值范围.
18. 已知函数 是奇函数,并且函数 的图象经过点 .
(1)求实数 、 的值及 的值域;
(2)解不等式 ;
第3页1
(3)若对任意 恒有 成立,求实数 的取值范围.
19已知函数
(1)设函数 是定义在 上的奇函数,当 时, ,求函数 的解析式;
(2)已知集合
①求集合 ;
②当 时,函数 的最小值为 ,求实数 的值.
大余县梅关中学 2024-2025 学年度高一上学期第二次月考
数学试卷
一、单选题
1.
【答案】B
2.
【答案】D
3.
【答案】A
4.
【答案】A
5.
【答案】D
6.
第4页1
【答案】D
7.
【答案】C
8.
【答案】D
二、多选题
9.
【答案】AC
10.
【答案】ABCD
11.
【答案】ABD
三、填空题
12.
【答案】
13.【答案】 ( 也对)
14. 已知 ,则 _______.
四、解答题
15.
【解析】
【分析】
(1)将 代入集合 ,解出 ,从而求出 .再求出 ,与集合 一起计算出
;
(2)解出集合 ,由 得 ,由子集关系可求得参数的范围.
【详解】(1)当 时, ,即
解得 ,即 ,则
第5页1
,
又 或 ,
;
(2)由 解得 ,
又 , ,即 ,
由 得 ,
, ,
,即 的取值范围是 .
16.
【解析】
【分析】(1)先根据 ,求出不等式的解,结合 可得 的值;
(2)利用换元法,把函数 转化为二次函数,结合二次函数区间最值法求解.
【小问1详解】
由 可得 ,又 ,所以 ,
又因为 的解集为 ,所以 ,
因为 ,所以 ,即 ,
解得 或 ,因为 ,所以 ;
【小问2详解】
第6页1
由(1)可得 ,
令 ,则 ,设 ,
①当 时, 在 上单调递增,
则 ,解得 ,符合要求;
②当 时, 在 上单调递减,在 上单调递增,
,解得 ,又 ,故 ;
③当 时, 在 上单调递减,
,解得 ,不合题意;
综上所述,存在实数 或 符合题意.
17.
【解析】
【分析】
(1)由f(x)<k,整理得:kx2﹣x+6k>0,然后,利用韦达定理进行求解
(2)把题目的成立条件转化为f(x) ≥g(x) ,进而分别求出,函数f(x)在区间[2,4]上的最小
最小值 最小值
值和函数g(x)在区间[2,4]上的最小值即可
【详解】(1)证明:由f(x)<k得: k,整理得:kx2﹣x+6k>0,因为解集为{x|﹣3<x<﹣2},
所以 k<0,所以方程kx2﹣x+6k=0的根是﹣3,﹣2,∴ 2+(﹣3),∴k ;
第7页1
所以实数k的值是 ;
(2)由题意可得,f(x) ≥g(x) ,
最小值 最小值
∀x∈[2,4],f(x) 在区间[2, ]为增函数,[ ,4]为减函数,f(2) ,f(4)
1
,
所以函数f(x)在区间[2,4]上的最小值是f(4) ;
函数g(x)开口向上,且对称轴x=﹣m,
①当﹣m≤2,即m≥﹣2,g(x) =g(2)=4+4m ⇒m ,解得:﹣2 ;
最小值
②当2<﹣m<4,即﹣4<m<﹣2,g(x) =g(﹣m)=m2﹣2m2 ⇒m≤﹣1或m≥1,所以﹣4
最小值
<m<﹣2;
③﹣m≥4,即m≤﹣4,g(x) =g(4)=16+8m ,解得:m ,所以m≤﹣4;
最小值
综上所述,m的取值范围:(﹣∞, ].
18.
【解析】
【分析】(1)根据奇函数的定义结合 可求得实数 、 的值;
(2)分析函数 的单调性,将所求不等式等价变形为 ,结合函数 的单调
性可得出关于 的不等式,解之即可;
(3)由函数 的单调性与奇函数的性质将所求不等式变形为 ,其中 ,利用
第8页1
参变量分离法结合对勾函数的单调性可求得实数 的取值范围.
【小问1详解】
因为函数 是奇函数,则 ,
即 ,
化简可得
所以 ,解得 或 .
又 ,所以 ,所以 , .
所以 ,
因为 ,则 ,所以 ,
所以 ,
的
即函数 值域为 .
【小问2详解】
由(1)得 ,
任取 、 ,且 ,则 ,
则 ,
所以 ,即函数 为 上的减函数,
由题意知: 在 上单调递减且为奇函数,
第9页1
所以 ,
所以 ,解得 或 ,
所以原不等式的解集为 或 .
【小问3详解】
由上可知: 在 上单调递减且为奇函数,
由 ,即 ,
即 ,即 ,
化简得: ,
又因为 ,当 时,对 恒成立,
当 时, ,
令 ,
令 ,则 ,
由对勾函数的性质知: 在 上单调递减,在 上单调递增,
,所以 .
19.
【解析】
【分析】(1)根据奇函数的性质求解即可;
(2)①由题知解 得 ,再解对数不等式即可得答案;
② 由 题 知 , 进 而 结 合 ① 还 原 , 转 化 为 求
第10页1
, 的最小值问题,再分类讨论求解即可.
【小问1详解】
解:根据题意,当 时, ,
当 时, ,则 ,
因为函数 是定义在 上的奇函数,
所以, ,
所以,
【小问2详解】
解:① ,即
所以,
所以, ,解得
所以,
②
由①可得
所以,函数 等价转化为 , ,
下面分三种情况讨论求解:
当 ,即 , 在 上 增函数,所以, ,
是
第11页1
解得 ,与 矛盾,舍;
当 ,即 时, 在 上是减函数,所以 ,解得
,满足题意;
当 , 即 时 , , 解 得 或
(舍)
综上: 的值为 或5
第12页