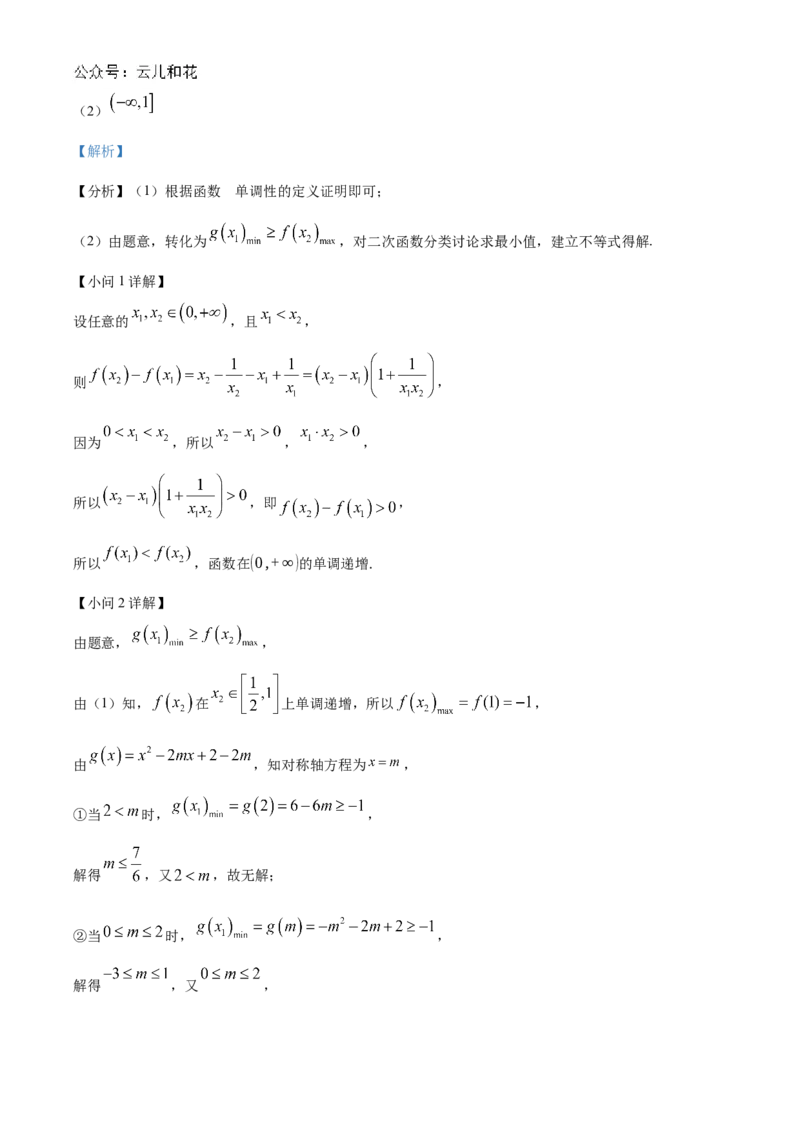文档内容
2024 学年第一学期宁波三锋教研联盟期中联考
科高一年级数学学科试题
考生须知:
1.本卷共4页满分150分,考试时间120分钟.
2.答题前,在答题卷指定区域填写班级、姓名、考场号、座位号及准考证号并填涂相应数字.
3.所有答案必须写在答题纸上,写在试卷上无效.
4.考试结束后,只需上交答题纸.
选择题部分
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是
符合题目要求的.
1. 已知集合 , ,若 ,则实数a的值为( )
.
A 0 B. 1 C. 1或3 D. 3
2. 下列函数中,既是偶函数,又是在区间(0,+∞)上单调递减的函数为( )
A. B. C. D.
3. “ ”是“ ” 的( )
A. 充分不必要条件 B. 必要不充分条件
C. 充要条件 D. 既不充分也不必要条件
.
4 , , ,则( )
A. B. C. D.
5. 下面不等式成立的是( )
A. 若 , ,则 B. 若 ,则
C. 若 ,则 D. 若 , ,则
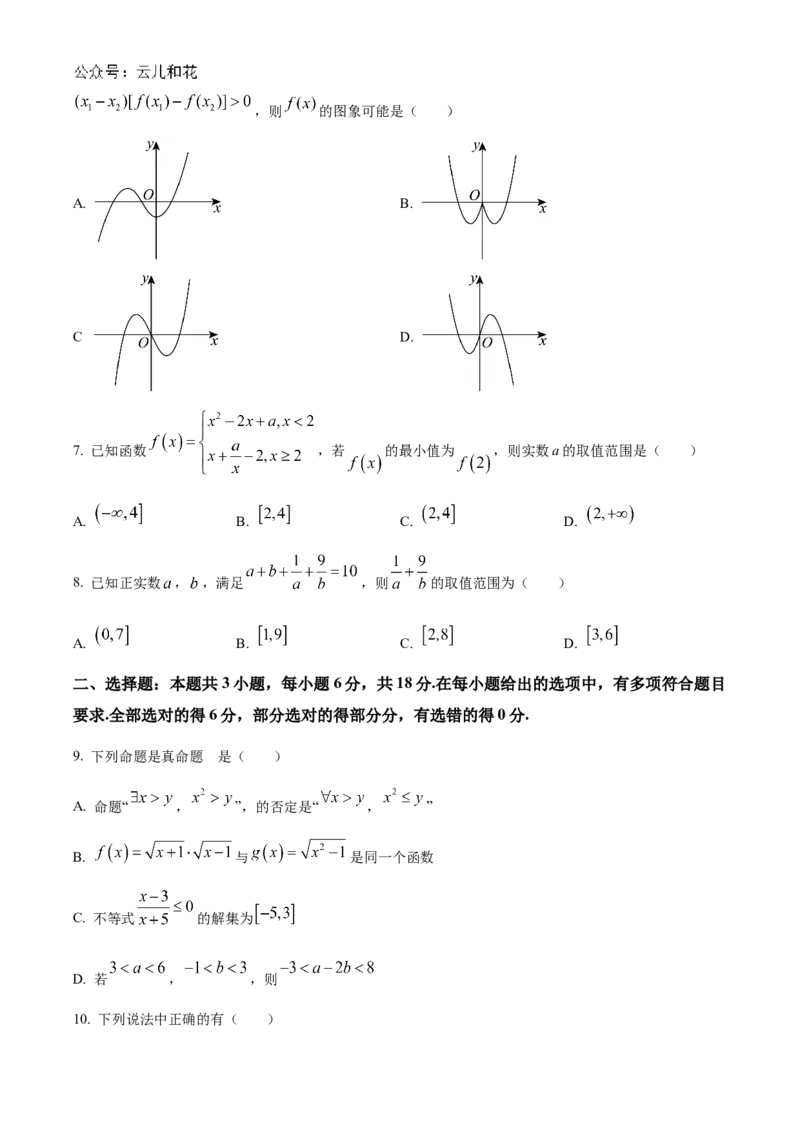
6. 已 知 函 数 的 图 象 关 于 点 对 称 , 且 , ,,则 的图象可能是( )
A. B.
C D.
.
7. 已知函数 ,若 的最小值为 ,则实数a的取值范围是( )
A. B. C. D.
8. 已知正实数 , ,满足 ,则 的取值范围为( )
A. B. C. D.
二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目
要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.
的
9. 下列命题是真命题 是( )
A. 命题“ , ”,的否定是“ , ”
B. 与 是同一个函数
C. 不等式 的解集为
D. 若 , ,则
10. 下列说法中正确的有( )A. 函数 在 上单调递增
B. 函数 的定义域是 ,则函数 的定义域为
C. 不等式 的解集为
D. 函数 关于点 中心对称
11. 已知函数 ,若 , 恒成立,则( )
A. 函数 是奇函数 B. 函数 是增函数
C. , 是真命题 D. m可以为0
非选择题部分
三、填空题:本题共3小题,每小题5分,共15分.
12. 函数 的单调递增区间为______.
13. 已知函数 是定义在 上的奇函数,且 时, ,则 _____.
14. 实数 , 满足 ,则 的最小值为______.
四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.
15. 函数 的定义域为集合 , , .
(1)求 , .
(2)若 ,求实数m的取值范围.
16. 已知函数
(1)若不等式 的解集为 ,求a,b的值(2)若方程 仅有一个实数解,求 的最小值.
17. 文化自信,服装先行,近年来汉服文化成为了一种时尚的潮流,“汉服热”的本质是对中华民族传统文化
的自觉、自知、自信.内育文化强底气,外引项目强经济,汉服体验项目的盛行也带动了文化古镇的经济发
展.近30天,某文化古镇的一汉服体验店,汉服的日租赁量P(件)与日租赁价格W(元/件)都是时间t
(天)的函数,其中 , .每件汉服的日综
合成本为20元.
(1)写出该店日租赁利润Y与时间t之间的函数关系;
(2)求该店日租赁利润Y的最大值.(注:租赁利润=租赁收入-租赁成本)
18. 已知函数 .
(1)用定义进行证明函数 在 的单调性.
(2)已知函数 ,若对任意的 , ,使得
,求实数m的取值范围.
19. 已知双曲函数 , .
(1)证明:
(2)判断函数 的单调性(不用证明),并解关于x的不等式 .
(3)若 ,不等式 成立,求实数 的取值范围.2024 学年第一学期宁波三锋教研联盟期中联考
科高一年级数学学科试题
考生须知:
1.本卷共4页满分150分,考试时间120分钟.
2.答题前,在答题卷指定区域填写班级、姓名、考场号、座位号及准考证号并填涂相应数字.
3.所有答案必须写在答题纸上,写在试卷上无效.
4.考试结束后,只需上交答题纸.
选择题部分
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是
符合题目要求的.
1. 已知集合 , ,若 ,则实数a的值为( )
A. 0 B. 1 C. 1或3 D. 3
【答案】D
【解析】
【分析】利用集合相等求解.
【详解】解:因为集合 , ,且 ,
所以 ,解得 ,
故选:D
2. 下列函数中,既是偶函数,又是在区间(0,+∞)上单调递减的函数为( )
A. B. C. D.
【答案】A
【解析】
【详解】试题分析:由偶函数定义知,仅A,C为偶函数, C. 在区间 上单调递增函数,故
选A.
考点:本题主要考查奇函数的概念、函数单调性、幂函数的性质.
点评:函数奇偶性判定问题,应首先考虑函数的定义域是否关于原点对称.3. “ ”是“ ”的( )
A. 充分不必要条件 B. 必要不充分条件
C. 充要条件 D. 既不充分也不必要条件
【答案】A
【解析】
【分析】利用充分条件、必要条件的定义,结合指数函数单调性判断即得.
【详解】 ,
反之当 时,取 ,不等式 无意义,
所以“ ”是“ ”的充分不必要条件.
故选:A
4. , , ,则( )
A. B. C. D.
【答案】D
【解析】
【分析】利用指数函数的性质比较大小即得.
【详解】 , ,
所以 .
故选:D
5. 下面不等式成立的是( )
A. 若 , ,则 B. 若 ,则
C. 若 ,则 D. 若 , ,则
【答案】B
【解析】【分析】举例说明判断AC;利用不等式的性质推理判断BD.
【详解】对于A,取 ,满足 , ,而 ,A错误;
对于B,由 ,得 ,则 ,B正确;
对于C,取 ,满足 ,而 ,C错误;
对于D,由 ,得 ,则 ,而 ,
于是 , ,D错误.
故选:B
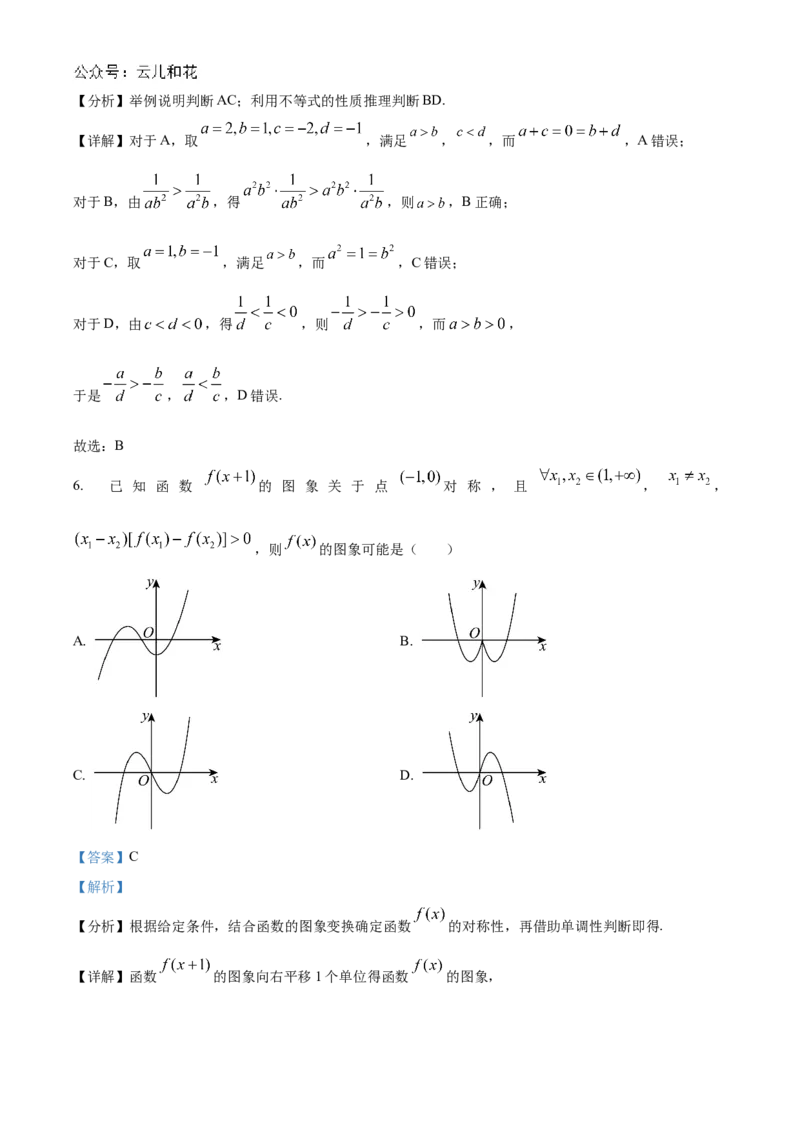
6. 已 知 函 数 的 图 象 关 于 点 对 称 , 且 , ,
,则 的图象可能是( )
A. B.
C. D.
【答案】C
【解析】
【分析】根据给定条件,结合函数的图象变换确定函数 的对称性,再借助单调性判断即得.
【详解】函数 的图象向右平移1个单位得函数 的图象,由函数 的图象关于点 对称,得函数 的图象关于原点对称,排除AB;
在
由 , , ,得函数 上单调递增,排除
D,C符合.
故选:C
7. 已知函数 ,若 的最小值为 ,则实数a的取值范围是( )
A. B. C. D.
【答案】B
【解析】
【分析】根据分段函数,分别确定每段的最小值,再根据给定最小值建立不等式,求解即可.
【详解】当 时, 的最小值为 ,
当 时, ,
若 时, 为增函数,所以 ,
所以需满足 ,解得 ,与 矛盾,故不合题意;
当 时,由对勾函数性质, 在 上单调递增,
又 的最小值为 ,则 ,解得 ,
综上,实数a的取值范围是 .
故选:B8. 已知正实数 , ,满足 ,则 的取值范围为( )
A. B. C. D.
【答案】C
【解析】
【分析】根据 ,由 ,得到
,再利用不等式和一元二次不等式的解法求解.
【详解】解:因为 ,
所以 ,即 ,
因为 ,则 ,解得 ,当且仅当
,即 或 时,等号成立,
所以 的取值范围为 ,
故选:C
二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目
要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.
9. 下列命题是真命题的是( )A. 命题“ , ”,的否定是“ , ”
B. 与 是同一个函数
C. 不等式 的解集为
D. 若 , ,则
【答案】AD
【解析】
【分析】根据存在命题的否定判断A,根据定义域不同判断B,根据特殊值判断C,根据不等式性质判断
D.
【详解】由存在量词命题的否定知, , ,的否定是 , ,故A正确;
由 知 的定义域为 ,由 或 知 定义域为
,所以函数不是同一个函数,故B错误;
因为 时,分母为0,故不等式的解集不是 ,故C错误;
由不等式的性质, ,又 ,
所以 ,故D正确.
故选:AD
10. 下列说法中正确的有( )
A. 函数 在 上单调递增
B. 函数 的定义域是 ,则函数 的定义域为
C. 不等式 的解集为D. 函数 关于点 中心对称
【答案】BD
【解析】
【分析】由复合函数的单调性可判断 A;由函数的定义域的定义可判断 B;对 讨论,分
,可判断C;由函数的图象平移可判断D .
【详解】对于A,函数 在 上单调递减,故A错误;
对于B,函数 的定义域是 ,可得 ,解得 ,所以函数 的定义
域为 ,故B正确;
对于C,不等式 ,当 时解集为 ;当 时解
集为 ;当 时解集为 ,故C错误;
对于D, 的图象可由 向左平移1个单位,再向上平移1个单位得到,可得
关于点 中心对称,故D正确.
故选:BD.
11. 已知函数 ,若 , 恒成立,则( )
A. 函数 是奇函数 B. 函数 是增函数
C. , 是真命题 D. m可以为0
【答案】ABC
【解析】
【分析】根据给定条件,结合奇函数的定义、复合函数的单调性,逐项分析判断即可.【详解】函数 的定义域为R,
对于A, , ,
函数 是奇函数,A正确;
对于B,函数 在R上单调递增,则函数 在R上单调递减,而 在R上单调递增,
因此函数 在R上单调递增,函数 是增函数,B正确;
对于C, ,
,因此 ,
, 是真命题,C正确;
对于D,由选项C知, ,解得 ,D错误.
故选:ABC
【点睛】思路点睛:涉及奇偶性的函数不等式,一般先利用函数的奇偶性得出区间上的单调性,再利用其
单调性脱去函数的符号“f”求解.
非选择题部分
三、填空题:本题共3小题,每小题5分,共15分.
12. 函数 的单调递增区间为______.
【答案】 (或(1,+∞)也正确)
【解析】
【分析】根据函数解析式直接得出单调区间.
【详解】 ,
所以函数 的单调递增区间为 .故答案为: (或(1,+∞)也正确)
13. 已知函数 是定义在 上的奇函数,且 时, ,则 _____.
【答案】
【解析】
【分析】由奇函数求出 ,再利用奇函数的定义求出 .
【详解】由函数 是定义在 上的奇函数,得 ,
而当 时, ,则 ,
所以 .
故答案为:
14. 实数 , 满足 ,则 的最小值为______.
【答案】2
【解析】
【分析】由条件分离出 ,代入 转化为关于 的式子,利用对数运算后由基本不等式求最值.
【详解】由 可得 ,
所以 ,
所以
,
当且仅当 ,即 , 时等号成立.
故答案为:2
【点睛】关键点点睛:本题的关键在于怎样建立已知条件与待求式之间的联系,通过类似消元的思想,利用对数运算与性质得出 ,再由均值不等式得解.
四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.
15. 函数 的定义域为集合 , , .
(1)求 , .
(2)若 ,求实数m的取值范围.
【答案】(1) , ;
(2) .
【解析】
【分析】(1)求出函数定义域化简集合 ,解不等式化简集合 ,再利用补集、交集的定义求解即得.
(2)由(1)的信息,利用并集的结果,结合集合的包含关系列式求解.
【小问1详解】
由 ,得 ,解得 ,则 ,
,由 ,得 ,则 ,
所以 , .
【小问2详解】
由 ,得 ,而 ,
则 ,解得 ,
所以实数m的取值范围是 .
16. 已知函数
(1)若不等式 的解集为 ,求a,b的值
(2)若方程 仅有一个实数解,求 的最小值.【答案】(1) 或
(2)
【解析】
【分析】(1)根据二次不等式的解集可知对应一元二次方程的根,由根与系数列方程求解;
(2)由题意判别式为0,得出 ,再由“1” 的技巧及基本不等式得解.
【小问1详解】
因为不等式 的解集为 ,
所以方程 的两根为 ,
所以由根与系数的关系可得 ,
解得 或 .
【小问2详解】
因为方程 仅有一个实数解,
所以 ,即 ,
所以 , ,
所以 ,当且仅当 ,即 时,等号成立,
所以 的最小值为 .
17. 文化自信,服装先行,近年来汉服文化成为了一种时尚的潮流,“汉服热”的本质是对中华民族传统文化
的自觉、自知、自信.内育文化强底气,外引项目强经济,汉服体验项目的盛行也带动了文化古镇的经济发
展.近30天,某文化古镇的一汉服体验店,汉服的日租赁量P(件)与日租赁价格W(元/件)都是时间t
(天)的函数,其中 , .每件汉服的日综
合成本为20元.
(1)写出该店日租赁利润Y与时间t之间的函数关系;
(2)求该店日租赁利润Y的最大值.(注:租赁利润=租赁收入-租赁成本)
【答案】(1)
(2)
【解析】
【分析】(1)按照“租赁利润=租赁收入-租赁成本”可以写出利润Y与时间t之间的函数关系;
(2)应用二次函数性质与对勾函数性质分段求出最大值,再比较两值大小即可得到利润Y的最大值.
【小问1详解】
解:依题意可知, ,
即
【小问2详解】解:因为 ,
所以当 时, ,
所以当 时 ;
当 时,
,
当且仅当 , ,
即 时等号成立,而 ,
由对勾函数性质可知 在 单调递减,
所以当 ,即 时, ,
又因为 ,
所以当 时,该店日租赁利润Y的最大值为 .
18. 已知函数 .
(1)用定义进行证明函数 在 的单调性.
(2)已知函数 ,若对任意的 , ,使得
,求实数m的取值范围.
【答案】(1)证明见解析(2)
【解析】
的
【分析】(1)根据函数 单调性的定义证明即可;
(2)由题意,转化为 ,对二次函数分类讨论求最小值,建立不等式得解.
【小问1详解】
设任意的 ,且 ,
则 ,
因为 ,所以 , ,
所以 ,即 ,
所以 ,函数在(0,+∞)的单调递增.
【小问2详解】
由题意, ,
由(1)知, 在 上单调递增,所以 ,
由 ,知对称轴方程为 ,
①当 时, ,
解得 ,又 ,故无解;
②当 时, ,
解得 ,又 ,所以 ;
③当 时, ,
解得 ,又 ,
.
所以
综上,实数m的取值范围 .
19. 已知双曲函数 , .
(1)证明:
(2)判断函数 的单调性(不用证明),并解关于x的不等式 .
(3)若 ,不等式 成立,求实数 的取值范围.
【答案】(1)证明见解析;
(2)单调递增, ;
(3) .
【解析】
【分析】(1)根据给定条件,利用指数运算计算即得.
(2)利用指数函数单调性,结合复合函数的单调性判断单调性,再利用单调性解不等式.
(3)根据给定条件,分离参数,换元并借助对勾函数的单调性求出最大值即可.
【小问1详解】
双曲函数 , ,
则 .【小问2详解】
函数 在 上单调递减, 在 上单调递增,而函数 在 上单调递增,
所以函数 在 上单调递增,
不等式 ,
则 ,即 ,解得 ,
所以原不等式的解集为 .
【小问3详解】
不等式 ,
当 时, ,则 ,
依题意, , 恒成立,令 , ,
,函数 在 上单调递增,
则当 时, ,因此 ,即当 时, 取得最大值 ,则 ,
所以实数 的取值范围是 .
【点睛】结论点睛:函数 的定义区间为 ,
①若 ,总有 成立,则 ;
②若 ,总有 成立,则 ;③若 ,使得 成立,则 ;
④若 ,使得 成立,则 .