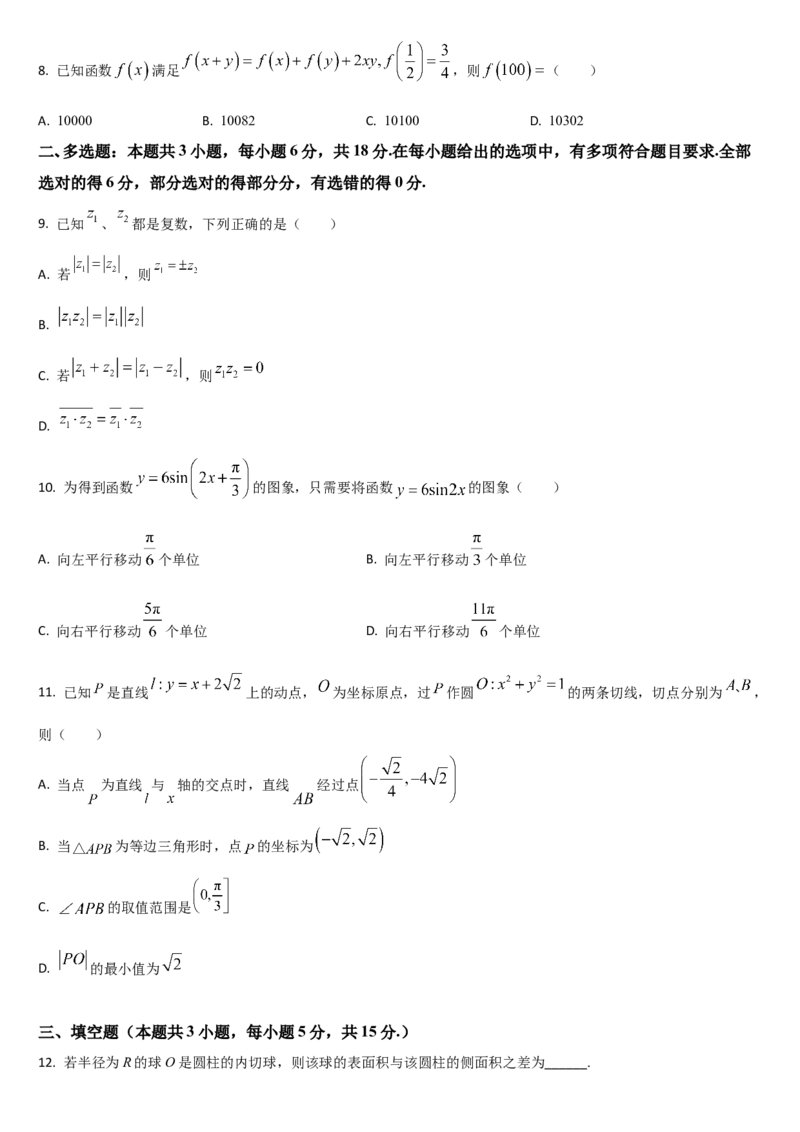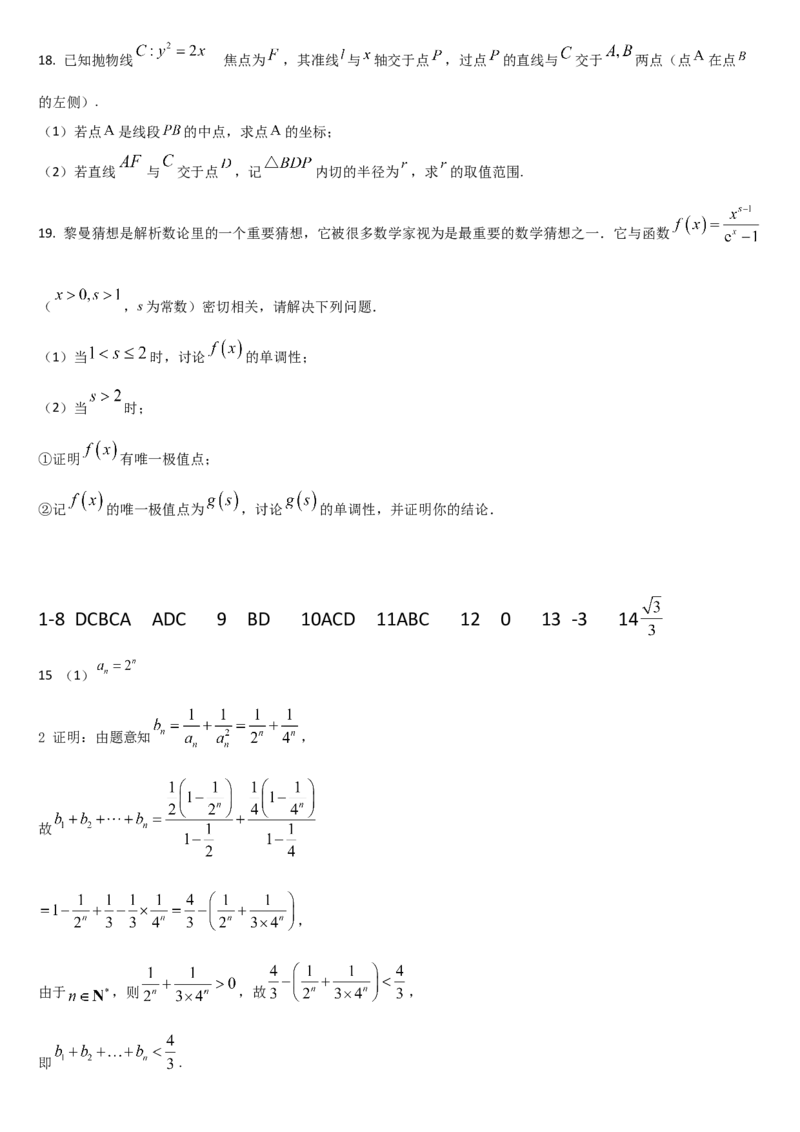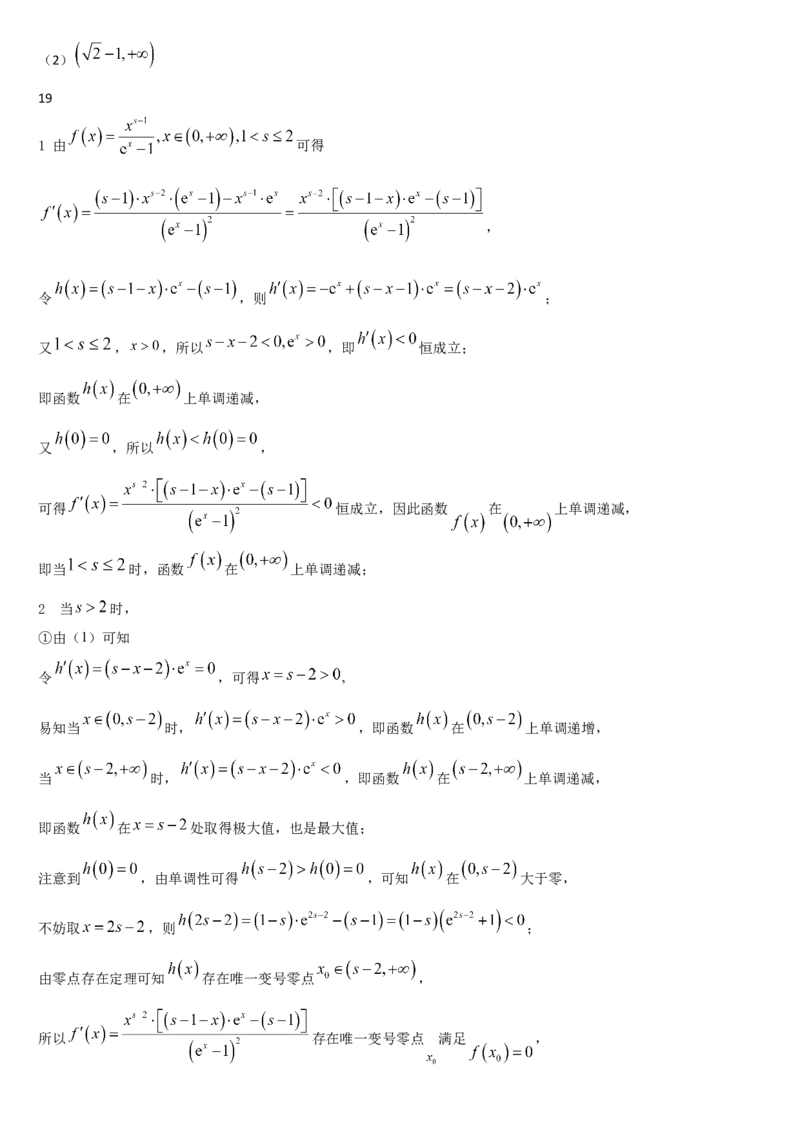文档内容
高三数学
一、选择题(本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.)
1.从某班所有同学中随机抽取10人,获得他们某学年参加社区服务次数的数据如下:4,4,4,7,7,8,8,9,
9,10,这组数据的众数是
A.9 B.8 C.7 D.4
2.已知向量 满足 ,则a(a-b)的值为
A.4 B.3 C.2 D.0
3.已知 , , ,则
A. B.
C. D.
4.已知椭圆G: ,A,B为G的短轴端点,P为G上异于A,B的一点,则直线AP,BP的斜
率之积为
A. B.
C. D.
5.标准对数视力表(如图)采用的“五分记录法”是我国独创的
视力记录方式.标准对数视力表各行“E”字视标约为正方形,
每一行“E”的边长都是上一行“E”的边长的 ,若视力 的视标边长约为10cm,则视力 的视标边长约为
A. B.
C. D.
6. 辽宁的盘锦大米以粒粒饱满、口感香糯而著称. 已知某超市销售的盘锦袋装大米的质量 (单位: )服从正态
分布 ,且 ,若从该超市中随机选取60袋盘锦大米,则质量在
的盘锦大米的袋数的方差为( )
A. 14.4 B. 9.6 C. 24 D. 48
7. 已知动点 在直线 上,过 总能作圆 的两条切线,切点为 ,且
恒成立,则 的取值范围是( )
A. B.
C. D.8. 已知函数 满足 ,则 ( )
A. 10000 B. 10082 C. 10100 D. 10302
二、多选题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部
选对的得6分,部分选对的得部分分,有选错的得0分.
9. 已知 、 都是复数,下列正确的是( )
A. 若 ,则
B.
C. 若 ,则
D.
10. 为得到函数 的图象,只需要将函数 的图象( )
A. 向左平行移动 个单位 B. 向左平行移动 个单位
C. 向右平行移动 个单位 D. 向右平行移动 个单位
11. 已知 是直线 上的动点, 为坐标原点,过 作圆 的两条切线,切点分别为 ,
则( )
A. 当点 为直线 与 轴的交点时,直线 经过点
B. 当 为等边三角形时,点 的坐标为
C. 的取值范围是
D. 的最小值为
三、填空题(本题共3小题,每小题5分,共15分.)
12. 若半径为R的球O是圆柱的内切球,则该球的表面积与该圆柱的侧面积之差为______.13. 在 的展开式中,含 的项的系数是______.(用数字作答)
14. 已知 为等腰三角形,其中 ,点D为边AC上一点, .以点B、D为焦点的椭圆E经过点
A与C,则椭圆E的离心率的值为______.
四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.
15. 已知数列 满足 .
(1)求 的通项公式;
(2)设 ,证明: .
在
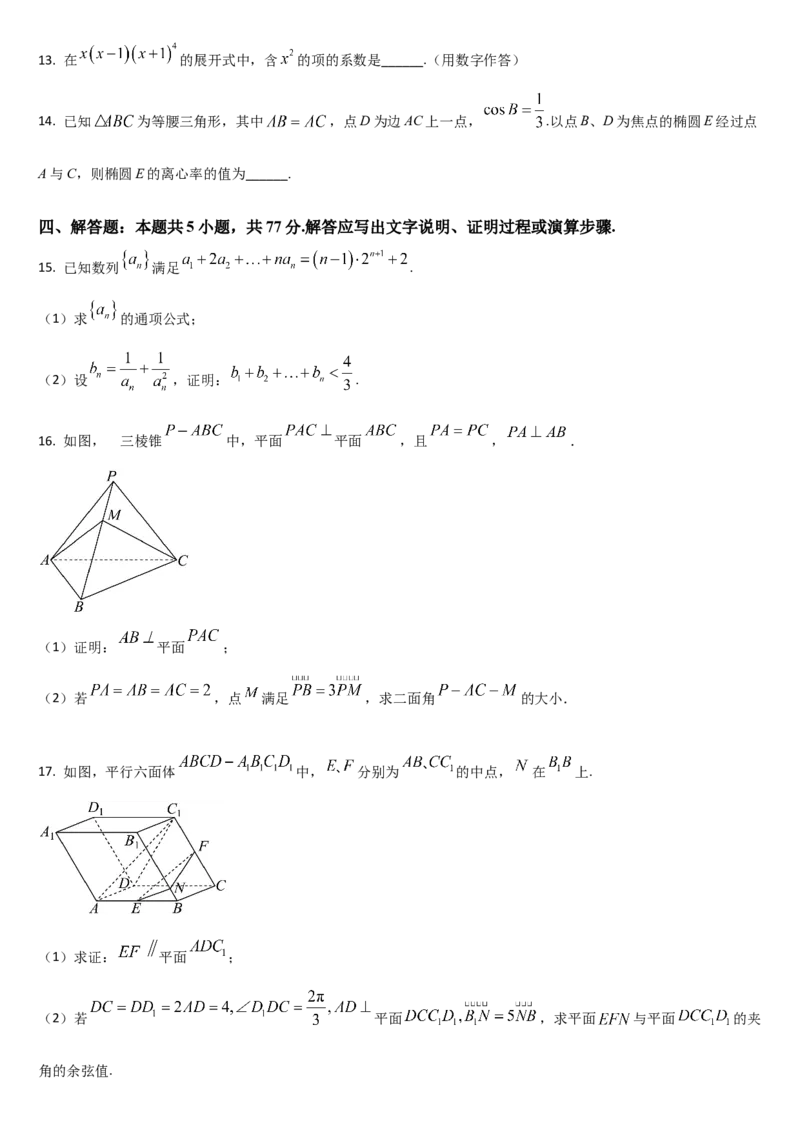
16. 如图, 三棱锥 中,平面 平面 ,且 , .
(1)证明: 平面 ;
(2)若 ,点 满足 ,求二面角 的大小.
17. 如图,平行六面体 中, 分别为 的中点, 在 上.
(1)求证: 平面 ;
(2)若 平面 ,求平面 与平面 的夹
角的余弦值.的
18. 已知抛物线 焦点为 ,其准线 与 轴交于点 ,过点 的直线与 交于 两点(点 在点
的左侧).
(1)若点 是线段 的中点,求点 的坐标;
(2)若直线 与 交于点 ,记 内切的半径为 ,求 的取值范围.
19. 黎曼猜想是解析数论里的一个重要猜想,它被很多数学家视为是最重要的数学猜想之一.它与函数
( ,s为常数)密切相关,请解决下列问题.
(1)当 时,讨论 的单调性;
(2)当 时;
①证明 有唯一极值点;
②记 的唯一极值点为 ,讨论 的单调性,并证明你的结论.
1-8 DCBCA ADC 9 BD 10ACD 11ABC 12 0 13 -3 14
15 (1)
2 证明:由题意知 ,
故
,
由于 ,则 ,故 ,
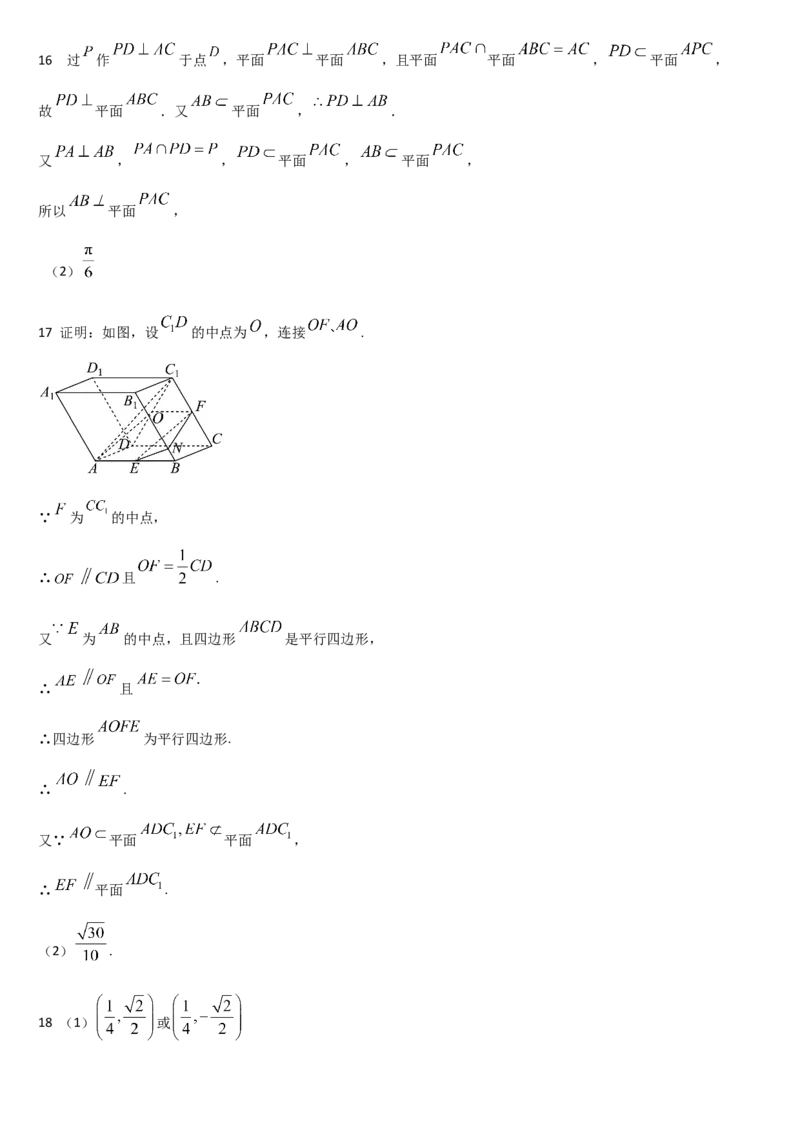
即 .16 过 作 于点 ,平面 平面 ,且平面 平面 , 平面 ,
故 平面 .又 平面 , .
又 , , 平面 , 平面 ,
所以 平面 ,
(2)
17 证明:如图,设 的中点为 ,连接 .
∵ 为 的中点,
∴ 且 .
又 为 的中点,且四边形 是平行四边形,
∴ 且
∴四边形 为平行四边形.
∴ .
又∵ 平面 平面 ,
∴ 平面 .
(2) .
18 (1) 或(2)
19
1 由 可得
,
令 ,则 ;
又 , ,所以 ,即 恒成立;
即函数 在 上单调递减,
又 ,所以 ,
可得 恒成立,因此函数 在 上单调递减,
即当 时,函数 在 上单调递减;
2 当 时,
①由(1)可知
令 ,可得 ,
易知当 时, ,即函数 在 上单调递增,
当 时, ,即函数 在 上单调递减,
即函数 在 处取得极大值,也是最大值;
注意到 ,由单调性可得 ,可知 在 大于零,
不妨取 ,则 ;
由零点存在定理可知 存在唯一变号零点 ,
所以 存在唯一变号零点 满足 ,由 单调性可得,当 时, ,当 时, ;
即可得函数 在 上单调递增,在 单调递减;
所以 有唯一极大值点 ;
②记 的唯一极值点为 ,即可得
由 可得 ,
即可得 的反函数 ,
令 , ,则 ,
构造函数 ,则 ,
显然 在 恒成立,所以 在 上单调递增,
因此 ,即 在 上恒成立,
而 ,即 ,所以 在 上恒成立,
即可得 在 上恒成立,因此 在 单调递增;
易知函数 与其反函数 有相同的单调性,所以函数 在 上单调递增;